“双减”背景下促进深度学习的初中数学专题复习的实践与思考

【摘要】复习课作为初中数学教学基本课型之一，是教学过程中一个重要的环节，是落实“四基”、发展“四能”的纽带．本文以“双减”的时代背景为依托，以“构造全等三角形”专题复习为例，探索促进深度学习的初中数学专题复习课教学策略．

【关键词】“双减”；深度学习；单元教学

复习课是初中数学课堂重要的授课方式之一，而专题复习课则是对学生理解存在困难的重难点进行强化、运用和迁移，可以在增强学生综合能力及创新意识的同时，同步培育核心素养．因此，本文基于“双减”政策背景，在进行专题复习课的教学设计时对知识进行重构和迁移，并灵活运用相关知识，充分调动学生主动参与，积极思考，从而进一步提高复习课堂学习效率．

1 深度学习的内涵及特征

深度学习是指在理解学习的基础上，学生能够批判性地学习新的思想和事实，并将它们融入原有的认知结构中，能够在众多思想间进行联系，并能够将已有的知识迁移到新的情境中，做出决策和解决问题．数学深度学习则是指在教师的引领下，学生围绕具有挑战性的数学学习主题，全身心积极参与、获得发展的有意义的学习过程.

不难发现，基于问题解决发展学生的高阶思维，提倡在具体情境中融入学生的切身体验，诱发学生学习的深层动机，这些就是深度学习的主要特征.

2 促进深度学习的专题复习课的设计理念

根据深度学习的特点，不难发现传统教学中缺乏整体架构的设计，难以在课堂教学过程中实现深度学习，因此数学单元教学思想是促进深度学习的根本．深度教学是促进学生深度学习的重要手段，有助于培养学生的核心素养［1］．深度教学强调教学过程中合理的问题引领，而专题复习课是对学生理解存在困难的重难点进行强化、运用和迁移［2］．

促进深度学习的专题复习课可以聚焦一个问题，围绕这个问题的核心思想与方法，向多维度延伸建构新的联系，实现迁移应用.

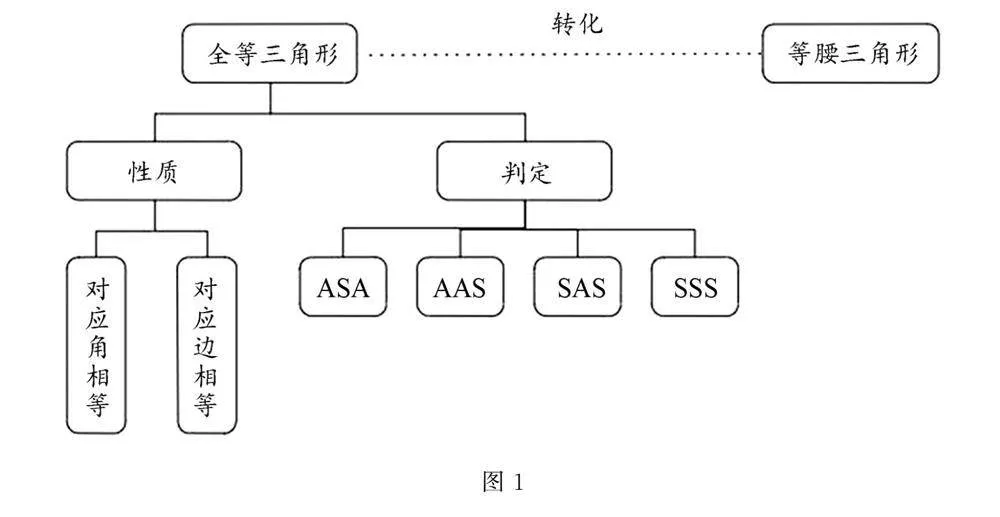
例如 以“构造全等三角形”的专题复习为例，围绕全等三角形单元的核心思想——构造全等三角形过程中蕴含的模型思想和在图形运动观点下的辅助线添加中隐藏的转化思想（见图1）.

3 促进深度学习的专题复习课的实施策略

3.1 情境创设，深度学习静静萌发

全等三角形的构造往往伴随着辅助线的添加，实现图形的转化，这是初中学生初学平面几何中常见的问题，体现几何直观，有助于学生感悟建模、转化、逻辑推理等数学思想，积累数学基本活动经验，掌握常规的分析方法，落实“双基”，为后续几何学习打好基础.但是，在实际学习过程中，辅助线怎么添？添几条？往哪儿添？这些问题却成为学生学好平面几何的“绊脚石”，他们容易受图形影响而找不到突破口，或是推理过程繁琐，逻辑漏洞百出.下面笔者以一次公开课的问题串设置，予以阐述.

问题1 如图2，在△BCD中，E是BC边上一点，且ED=CD，判断∠BED与∠C的数量关系，并说明理由．

问题2 如图3，在△BCD中，E是BC边上一点，且ED = CD，将△BED沿直线BD翻折，点E的对应点为点A，判断∠A与∠C的数量关系，并说明理由．

通过问题1和问题2的设置，帮助学生回顾了等腰三角形和全等三角形的相关知识，同时引导学生关注角的平分线在图中所起到的作用，为问题3中辅助线的添加提供合理的思考方向，深度学习正在萌芽.

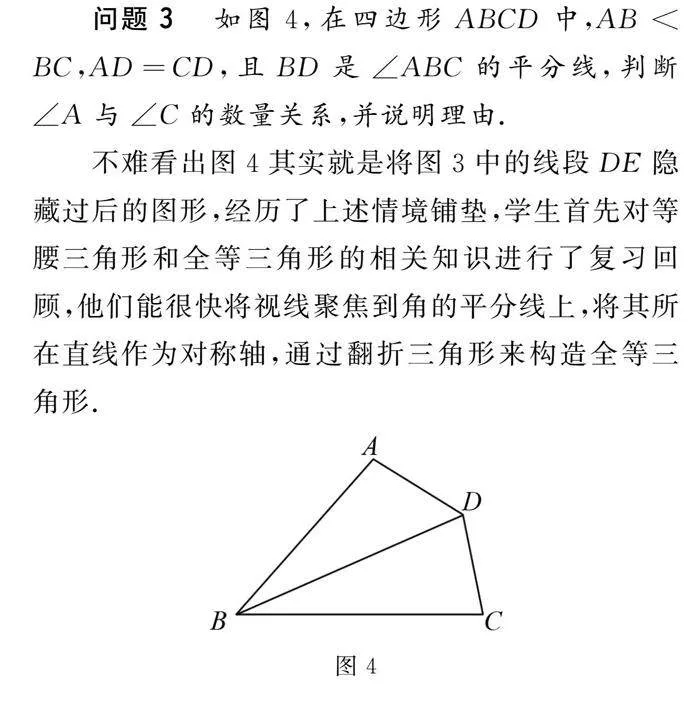
问题3 如图4，在四边形ABCD中，AB< BC，AD=CD，且BD是∠ABC的平分线，判断∠A与∠C的数量关系，并说明理由．

不难看出图4其实就是将图3中的线段DE隐藏过后的图形，经历了上述情境铺垫，学生首先对等腰三角形和全等三角形的相关知识进行了复习回顾，他们能很快将视线聚焦到角的平分线上，将其所在直线作为对称轴，通过翻折三角形来构造全等三角形.

3.2 巧妙变式，深度学习悄然生长

根据下列条件，添加适当的辅助线，构造全等三角形.

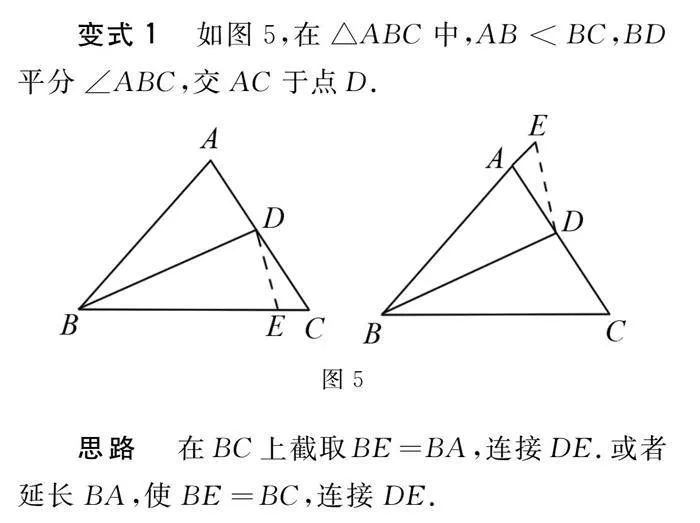
变式1 如图5，在△ABC中，AB<BC，BD平分∠ABC，交AC于点D．

思路 在BC上截取BE=BA，连接DE．或者延长BA，使BE=BC，连接DE．

当研究对象从四边形转化成三角形时，线段BD作为三角形的角平分线，同样可以利用其所在直线作为对称轴，将三角形进行翻折，从而构造全等三角形．

变式2 将变式1中的条件略作变化，即AB=BC，此时△ABC是等腰三角形.根据等腰三角形顶角的平分线与底边上的高重合，从三角形的角平分线过渡到三角形的高，进一步引出变式3讨论以不等边三角形一边上的高所在直线为对称轴，翻折三角形，从而构造全等三角形，并引导学生发现如此添加辅助线不仅能构造全等三角形，更能形成等腰三角形这一事实．

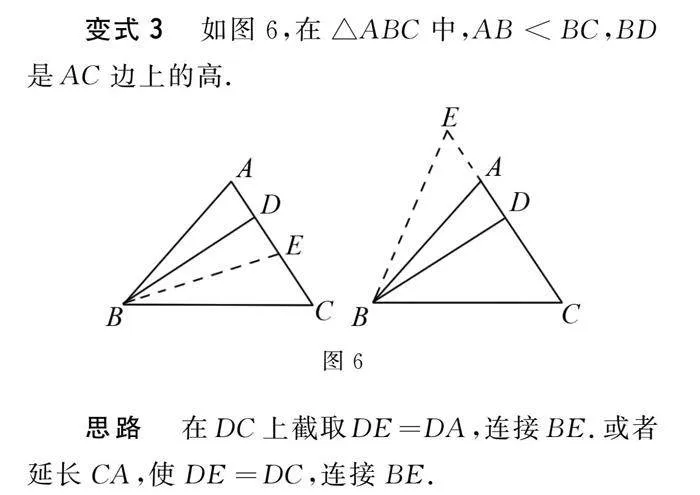
变式3 如图6，在△ABC中，AB<BC，BD是AC边上的高．

思路 在DC上截取DE=DA，连接BE．或者延长CA，使DE=DC，连接BE．

设计一组变式引领学生主动思考，有助于学生发掘问题的本质，并在现有经验的基础上进一步探索新的方法和规律.因此有效的变式教学有助于促进学生的深层学习.

3.3 推陈出新，深度学习热烈绽放

类似变式2，由等腰三角形的三线合一，引发学生思考：对于已知不等边三角形的中线，如何恰当的添加辅助线，构造全等三角形．

根据既往经验，部分学生会依样画葫芦，模仿前述变式，利用三角形中线所在直线作为对称轴，翻折三角形从而构造全等三角形，但如图6所示，这种辅助线的添加方式并不能为推理说明提供有效的条件.因而，对于已知不等边三角形的中线，通过轴对称变换进行辅助线的添加是不合适的.

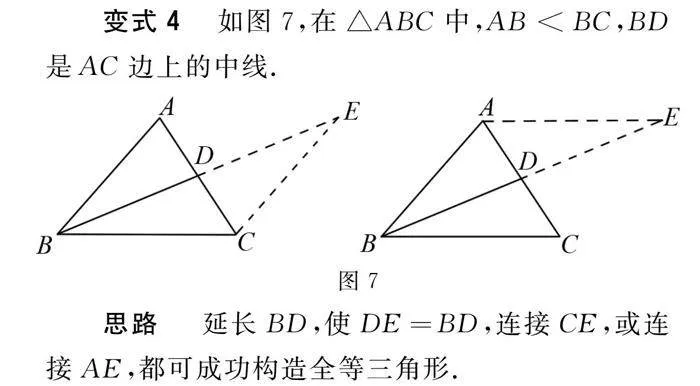
变式4 如图7，在△ABC中，AB<BC，BD是AC边上的中线．

思路 延长BD，使DE=BD，连接CE，或连接AE，都可成功构造全等三角形.

此时我们可以通过加倍延长中线，相当于是利用图形的中心对称来构造全等三角形．

例题 如图8，在△ABC中，AC<AB，AD是BC边上的中线，E是AC上一点，BE交AD于点F，且AE＝EF．判断线段AC与线段BF的数量关系，并说明理由．

思路 延长AD，使DG=AD，连接BG．则易得△ADC≌△GDB，进一步推得AC=BG，再利用等腰三角形的性质和对顶角相等可知BF=BG，则有AC=BF．

学生学习数学知识，不仅要理解掌握，更要学会运用数学的思维去类比迁移，探索新知，实现触类旁通，举一反三，这才是数学思维的生长点［3］.

3.4 总结反馈，深度学习硕果累累

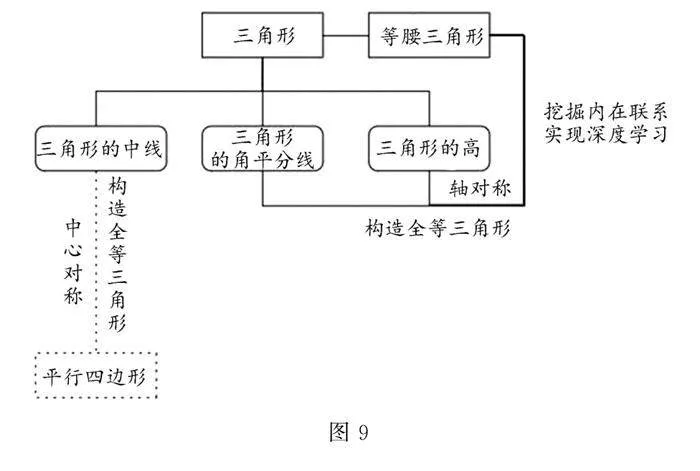
课堂学习后的总结、反思与回顾是提高学生深度学习能力的重要环节，及时的总结反馈能更好地帮助学生重新构建认知结构，提炼基本方法，感悟思想方法.可以引导学生自主小结，以思维导图（如图9所示）的形式呈现课堂收获，实现深度学习，并进一步提升核心素养，巩固学习成果.

4 结语

三角形是最简单的平面线型封闭图形，学生在小学阶段对三角形已经具备了初步的认识，进入初中阶段后又进一步了解了有关特殊三角形的性质、两个三角形全等的概念和性质、全等三角形的判定方法等知识．学习三角形的相关知识是进一步探究和学习其他图形性质的基础．

因此，教师在进行教学设计时必须静下心来认真钻研，设置行之有效的变式，让学生在螺旋上升的学习过程中激发他们学习的深层动力.在课堂教学过程中，有效提问，符合学生的基本活动经验，注重新旧知识之间的区别与联系，将它们有效融合，引发学生的认知冲突，进一步促进学生的深层学习，最终提升发现问题并解决问题的能力.

参考文献：

［1］郑毓信.“数学深度教学”的理论与实践［J］.数学教育学报，2019，28（05）：24-32.

［2］许婷婷.“双减”背景下提高初中数学复习课效能的策略研究［D］.重庆：西南大学，2022.

［3］牛星惠．数学抽象素养的达成特点与培养［J］．中学数学教学参考（中旬），2018（07）：27-32.