初中数学图象信息问题解题技巧

【摘要】图象信息问题，是初中数学解题中的常见题目类型，要求学生根据题目中的数据、图表信息，寻求题目中隐藏的数学关系，根据信息把握问题特征，找出解题方向，同时利用图表相关知识解决问题.本文根据沪科版初中数学教材，结合常见的几种图象信息问题进行展示，帮助学生掌握此类问题的解题技巧，以期为提高学生解题能力提供有价值的借鉴资料.

【关键词】图象信息；初中数学；解题技巧

根据《义务教育数学课程标准》中的解释，数学是一门普遍适用的技术，有助于人们收集、整理与描述信息，利用数学知识为社会创造价值.数学信息搜集整理与利用，是学生应当具备的数学学习能力，也是学生学习数学过程中逐渐形成的基本数学素养［1］.在初中数学解题中，有一类问题是图象信息问题，考查学生对信息的搜集与整理能力，也要求学生具备一定的读图识图、利用图象寻找题目隐藏信息的能力.一般来说，图象信息问题的题干描述较为复杂，且存在较多的隐藏条件，这就需要学生灵活运用图表相关知识，发挥自身识读与信息加工整理能力，解决问题.

1 利用表格数据，转化信息解决问题

表格数据类的图象信息问题，是较为常见的题目类型，也是较为简单的题目.针对此类问题，学生需要根据题目的具体情况，对表格中的数据研究对象、数据分布情况进行分析，比如，若是用于方程组的数据，则可以通过收集与整合其中数据，发现两个变量的关系，构建相应的数学模型，作为解题方法.明确表格中的数据研究对象之后，需要找到表格中每个项目所对应的数据，将这些数据整合起来，作为解决问题的辅助信息［2］.同时，找到表格内各项目对应的数据，也有助于分析表格各数据之间的关系，便于学生对表格内数据进行加工，确定解题方向，从而找到合适的数学知识转换题目内已有信息，解决问题.

例1 某自然风景区为了让行人更好地在园内休闲娱乐，决定修建一条长为6千米的蜿蜒盘旋的景观步道.在工程准备阶段，设计人员提出：假设平均每天的修建费z（万元）与修建天数x（天）之间在30≤x≤120范围内具有一次函数的关系，如表1所示，请解决下面问题：

（1）求z关于x的函数关系式；

（2）后来工程施工过程中，修建计划发生改变，建设方决定增加2千米的外延景观道，在没有增减建设力量的情况下这个工程的完工时间比预期晚了15天，请问原本施工计划中每天的修建费用是多少？

解析 这道题是一道经典的图象信息类问题，考查学生的图表信息提取与分析能力，要求学生准确读表，提取表格内的数据与数量关系，并且利用数学知识对图表内信息进行转化，将实际问题转化为数学问题，最终求解，得到b关于a的函数关系式、原本计划每天的修建费用.

解题过程：

（1）根据表格确定两对数字，将其导入关系方程中，列出方程组，求解.假设z关于x的函数关系式是z=kx+b.根据表格，可以知道x=50时，z=40；x=60时，z=38.因此，40=50k+b，38=60k+b，求解得到k=-15，b=50.因此可以得到z关于x的函数关系式是z=-15x+50

（2）根据题目信息与表格，可以得到6x=8x+15，x=45.因此，x=45时，z=-15x+50=-15×45+50=41，故原本施工计划中每天的修建费用是41万元.

2 利用图示信息，整合加工辅助解题

识图，是初中图表信息问题解题的小技巧之一.掌握识图技巧，不仅可以从图表中获取有用的信息，也可以对这些信息进行加工处理，促使其以一个具体的问题呈现出来，便于学生之后利用数学知识解决问题［2］.

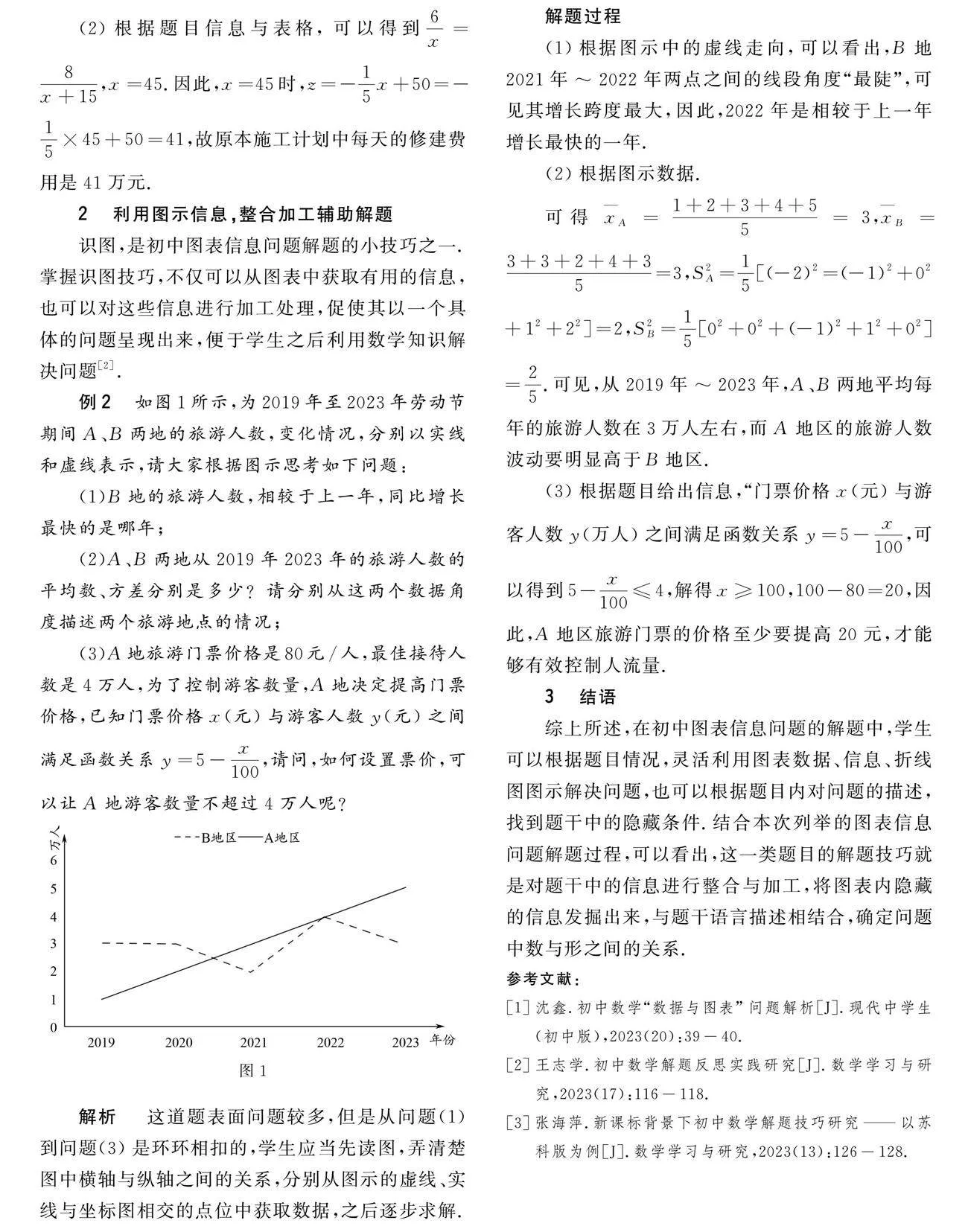
例2 如图1所示，为2019年至2023年劳动节期间A、B两地的旅游人数，变化情况，分别以实线和虚线表示，请大家根据图示思考如下问题：

（1）B地的旅游人数，相较于上一年，同比增长最快的是哪年；

（2）A、B两地从2019年2023年的旅游人数的平均数、方差分别是多少？请分别从这两个数据角度描述两个旅游地点的情况；

（3）A地旅游门票价格是80元/人，最佳接待人数是4万人，为了控制游客数量，A地决定提高门票价格，已知门票价格x（元）与游客人数y（元）之间满足函数关系y=5-x100，请问，如何设置票价，可以让A地游客数量不超过4万人呢？

解析 这道题表面问题较多，但是从问题（1）到问题（3）是环环相扣的，学生应当先读图，弄清楚图中横轴与纵轴之间的关系，分别从图示的虚线、实线与坐标图相交的点位中获取数据，之后逐步求解.

解题过程

（1）根据图示中的虚线走向，可以看出，B地2021年～2022年两点之间的线段角度“最陡”，可见其增长跨度最大，因此，2022年是相较于上一年增长最快的一年.

（2）根据图示数据.

可得xA=1+2+3+4+55=3，xB=3+3+2+4+35=3，S2A=15［（-2）2=（-1）2+02+12+22］=2，S2B=15［02+02+（-1）2+12+02］=25.可见，从2019年～2023年，A、B两地平均每年的旅游人数在3万人左右，而A地区的旅游人数波动要明显高于B地区.

（3）根据题目给出信息，“门票价格x（元）与游客人数y（万人）之间满足函数关系y=5-x100，可以得到5-x100≤4，解得x≥100，100-80=20，因此，A地区旅游门票的价格至少要提高20元，才能够有效控制人流量.

3 结语

综上所述，在初中图表信息问题的解题中，学生可以根据题目情况，灵活利用图表数据、信息、折线图图示解决问题，也可以根据题目内对问题的描述，找到题干中的隐藏条件.结合本次列举的图表信息问题解题过程，可以看出，这一类题目的解题技巧就是对题干中的信息进行整合与加工，将图表内隐藏的信息发掘出来，与题干语言描述相结合，确定问题中数与形之间的关系.

参考文献：

［1］沈鑫.初中数学“数据与图表”问题解析［J］.现代中学生（初中版），2023（20）：39-40.

［2］王志学.初中数学解题反思实践研究［J］.数学学习与研究，2023（17）：116-118.

［3］张海萍.新课标背景下初中数学解题技巧研究——以苏科版为例［J］.数学学习与研究，2023（13）：126-128.