平面图形与立体图形之间的转化关系

【摘要】本文深入研究了平面图形与立体图形之间的转化关系，探讨了从不同角度观察、展开、折叠和旋转等几个方面的具体问题.通过这些问题的求解，得出了平面图形和立体图形之间独特而丰富的关联，为几何学和图形学领域提供了新的理解和认识.

【关键词】平面图形；立体图形；转化关系

1 从三个方向看，用平面图形表示立体图形

例1 由若干个完全相同的小正方体组成一个立体图形，它的左视图和俯视图如图1所示，则小正方体的个数不可能是（ ）.

（A）5. （B）6. （C）7. （D）8.

分析 直接利用左视图以及俯视图进而分析得出答案．

解答 由左视图可得，第2层至少有一个小立方体，第1层一共有5个小立方体，故小正方体的个数最少为：6个，故小正方体的个数不可能是5个．故选（A）．

点评 此题主要考查了由三视图判断几何体，正确想象出所用正方体最少时的几何体的形状是解题关键．

2 将立体图形展开为平面图形

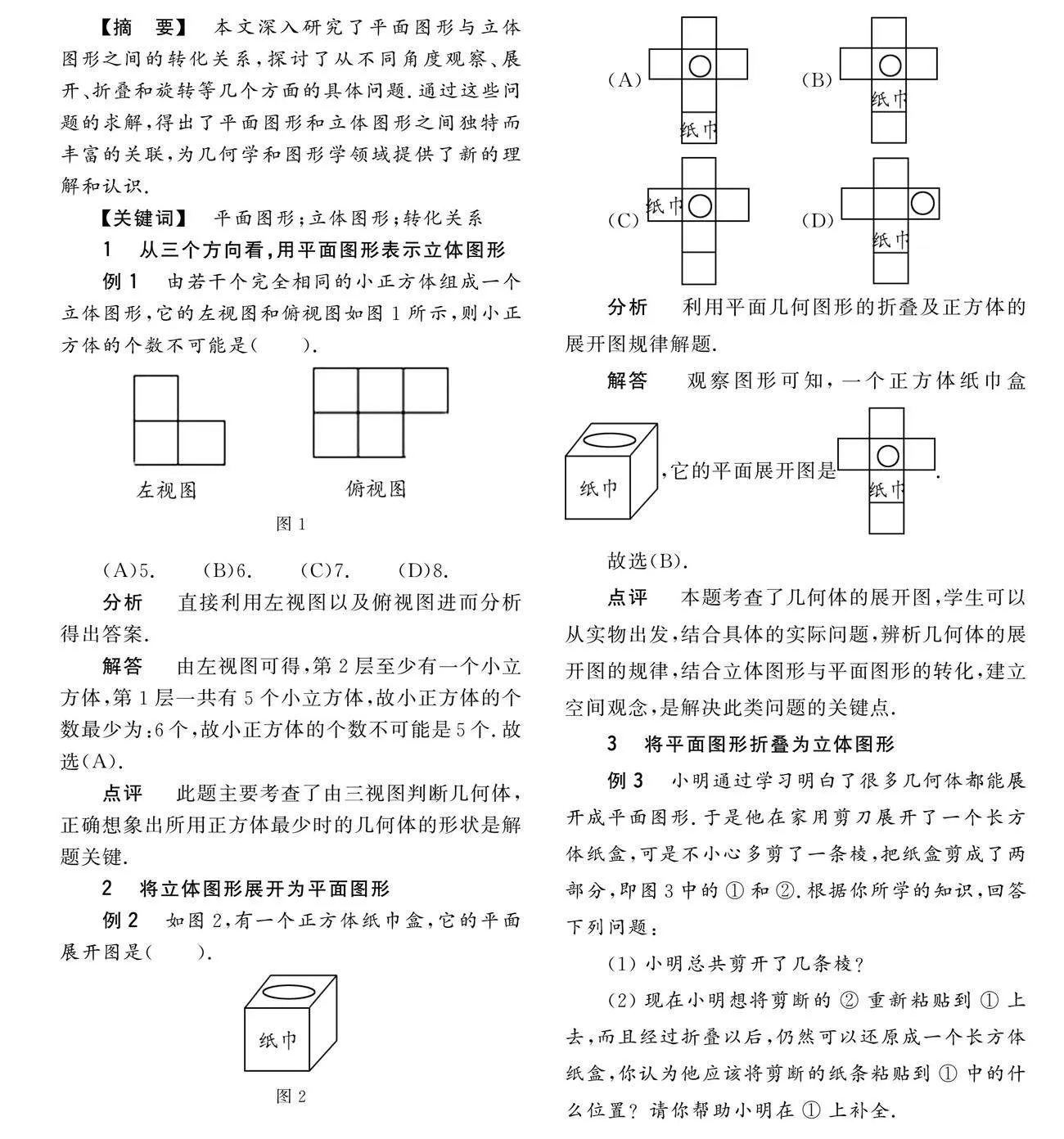
例2 如图2，有一个正方体纸巾盒，它的平面展开图是（ ）.

（A） （B）

（C）（D）

分析 利用平面几何图形的折叠及正方体的展开图规律解题．

解答 观察图形可知，一个正方体纸巾盒，它的平面展开图是．

故选（B）．

点评 本题考查了几何体的展开图，学生可以从实物出发，结合具体的实际问题，辨析几何体的展开图的规律，结合立体图形与平面图形的转化，建立空间观念，是解决此类问题的关键点．

3 将平面图形折叠为立体图形

例3 小明通过学习明白了很多几何体都能展开成平面图形．于是他在家用剪刀展开了一个长方体纸盒，可是不小心多剪了一条棱，把纸盒剪成了两部分，即图3中的①和②．根据你所学的知识，回答下列问题：

（1）小明总共剪开了几条棱？

（2）现在小明想将剪断的②重新粘贴到①上去，而且经过折叠以后，仍然可以还原成一个长方体纸盒，你认为他应该将剪断的纸条粘贴到①中的什么位置？请你帮助小明在①上补全．

分析 （1）根据①所示的图形，并结合长方体的立体图形，即可得到一共要剪几条棱；

（2）将①进行简单折叠后可以发现，要想还原成长方体还缺少与①中下方小长方形相对的一面，据此可得出②可以粘贴的一个位置；由图3可知，需将②粘贴在①的上方相对或隔一个相对位置，接下来自己试着分析②中长方形的宽与①中小长方形的宽相同的情况吧．

解答 （1）小明总共剪开了8条棱；

（2）如图4，有以下四种可选择的位置：

点评 本题考查了几何体的展开图，结合具体的实际问题，辨析几何体展开图，通过立体图形与平面图形之间的转化，建立空间观念，解决此类问题．

4 将平面图形旋转成立体图形

例4 如图5，一个边长为2的正方形与等腰直角三角形的一边重合，组成一个平面图形，将它绕AB所在直线按逆时针方向旋转180°，得到的几何体体积为163π．（圆锥的体积公式为：V圆锥＝13πr2h）

分析 这一平面图形绕AB所在直线，按逆时针方向旋转180°，得到一个由半个圆锥和半个圆柱组成的几何体，依据圆锥的体积公式和圆柱的体积公式进行计算即可．

解答 该图形绕AB所在直线按逆时针方向旋转180°，得到一个由半个圆锥和半个圆柱组成的几何体，这一几何体的体积＝12×（13π×22×2+π×22×2）＝163π，

故答案为：163π．

点评 本题主要考查了几何体的体积，解决问题的关键是掌握圆锥的体积公式和圆柱的体积公式．

5 结语

通过对平面图形与立体图形转化关系的深入研究，揭示了图形学中的一些有趣而实用的原理.这一研究为计算机图形学、建筑设计等领域提供了理论支持，同时也为学生提供了更生动、形象的学习方法.

参考文献：

［1］朱勇.旋转，建立平面与立体的关联——《圆锥的体积（练习）》教学与思考［J］.教育视界，2023（23）：63-66.

［2］刘露，黄云龙，汤艳.图形与几何［J］.贵州教育，2023（Z1）：39-46.

［3］王欢.复习课，不妨从学生的认知平衡入手——《立体图形表面积和体积（复习）》设计与思考［J］.教育视界，2022（17）：63-65.