在思考中探索 在拓展中创新

【摘要】解题能力的培养需要教师在课堂教学中通过思考、探究，延伸知识点，拓展解题思路以及创新解题等方式深挖相关的例题，引导学生进行科学有序的训练.本文通过探究几个数学例题，论述解题能力培养的重要性，帮助学生从例题中发现更深层次的规律和思维方法，培养学生的逻辑思维、分析问题的能力，并促进他们的创新思维能力得到发展.

【关键词】初中数学；解题能力；探究；创新

中考是评价学生数学水平的重要考试，教师需要指导学生运用解题思路解决各种类型的数学问题.而数学中的经典例题需要进行思考并探索其考查的知识点，进而形成系统的知识框架.如果只是停留在例题表面，可能会陷入“模式化思维”，因此需要对这些例题进行革新与拓展，从而促进学生的思维发展，提高学生的综合素养和解题能力.即通过对例题进行更深层次的探索和研究，将其进行拓展与创新，可以激发学生的思维，增强他们的解题能力.从不同的角度来解题，培养学生灵活运用知识的能力，使他们能够更好地理解和应用数学概念，提高他们解决问题和应对挑战的能力.

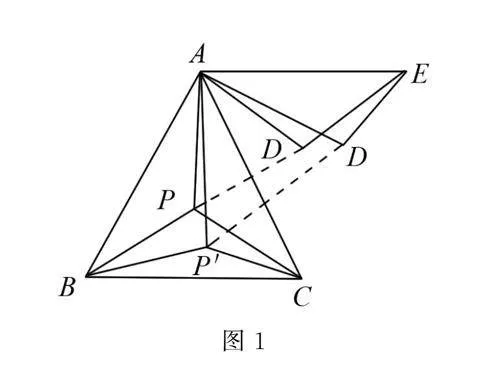
例1 如图1所示，点P为等边三角形ABC的中心，△ADE与△ACP全等，∠PAD=60°，连接PD，可得PD=PA，由此可知△APD为等边三角形，则∠BPD=180°，∠PDE=180°，那么点E、点D、点P和点B在一条直线上，因此PA，PB和PC之和等于PD，PB和DE之和，且数值上等于BE.在△ABC中，取一点P′，该点到点A、点B和点C的连线所形成的夹角固然是不相等，那么点B、点P′、点D′和点E不在一条直线上，所以P′A，P′B和P′C之和大于PA，PB和PC之和，即点P到点A、点B和点C的距离之和最小.

探究 如图2所示，P在△ABC中，∠APB，∠BPC和∠APC相等，证明点P到点A、点B和点C的距离之和最小.

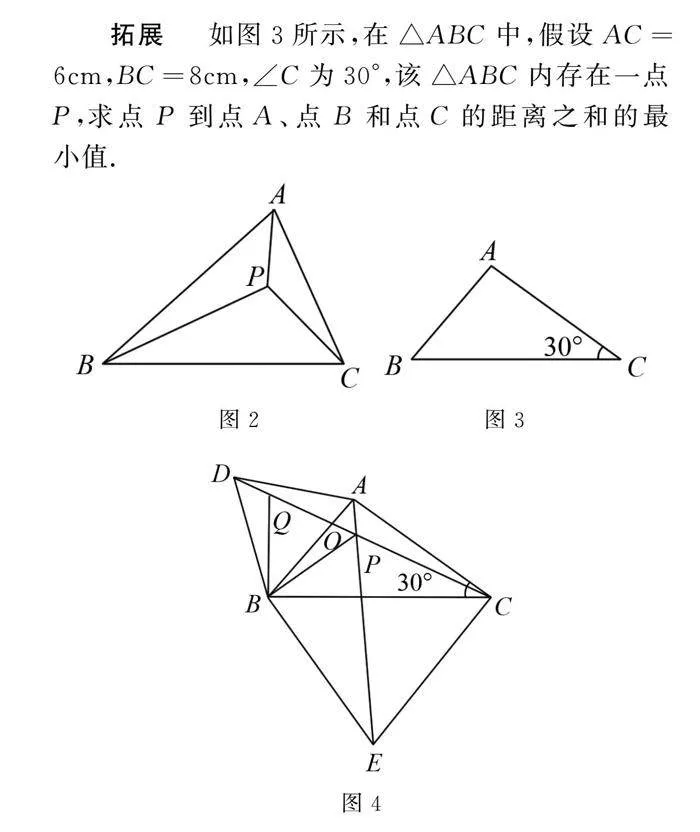
拓展 如图3所示，在△ABC中，假设AC=6cm，BC=8cm，∠C为30°，该△ABC内存在一点P，求点P到点A、点B和点C的距离之和的最小值.

分析 探究题是例1的一个问题的转化，同样是点P到三角形顶点的距离问题，以例1为启示进行拓展，如图4所示，分别以AB，BC为边向外作等边三角形，同样连接CD，AE交于点P，进而证明△ABE与△DBC全等，可得CD=AE，∠BAE=∠BDC，在DO上取一点Q，使DQ=AP，则△ABP和△DBQ全等，故可证得△PBQ为等边三角形，那么PB=PQ，可得点P到点A、点B和点C的距离之和等于DQ，PQ和PC之和，且与CD，AE相等，再根据勾股定理便可算出AE.

变式1 如图5所示，∠ACB=∠CBA=∠DCE=∠CED = 60°，点A，点D和点E这3点共线，连接BE.

①∠AEB的度数为60°;

②线段AD，BE之间的数量关系为AD = BE.

变式2 如图6所示，AC=BC，DC=CE且∠ACB和∠DCE均为直角，点A、点D和点E三点共线，过C点作△DCE的高CM与DE相交于点M，连接BE，求∠AEB的度数以及CM，AE，BE的关系.

yXm8Jh8rYCc2C0nSvZNtLxgSaIHpZyXiF+7N8PmYyGk=分析 变式1：根据题意可知△ACB和△DCE均为等边三角形，△ACD和△BCE全等，进而可知AD=BE，∠ADC=∠BEC.点A，点D和点E这3点共线能够求出∠ADC，进而∠AEB的度数便可求出.

变式2：根据变式1中的解法可求出∠AEB以及AD = BE；由题意可知△ABC和△DCE均为等腰直角三角形，可得CM =DM = ME，进而求出CM，AE，BE的关系为AE = 2CM +BE.

例2 如图7所示，AB =10，∠B为60°，△ABC的边AB和BC上存在点D和点E，BD = BE =4，△B′DE是通过△BDE沿DE翻折所得，将点A和点B′连接，试求AB′的长.

分析 在本题当中，关键点在于构造直角三角形，使用勾股定理寻求边之间的关系，因此我们过点D作B′E的垂线交于点F，过点B′作AD的垂线交于点G，如图8，∠B=60°，则△BDE为等边三角形，且边长等于4.△B′DE是通过翻折所得，故其也为等边三角形，GD=B′F=2，B′D=4，由勾股定理可得：B′G= B′D2－GD2，进而计算可知B′G=23，则AB=10，即AG=10-6=4，最终可计算AB′的长度.

拓展 如图9所示，四边形ABCD为矩形，以GH为对折线折叠，点Q和点E分别为点C和点D的落点，EQ和BC交于点F，AD=8，AB=6，AE=4，试求△EBF的周长.

分析 该题与例2同为图形的折叠，把握矩形的特性以及折叠过来之后图形的关系，通过例2进行举一反三即可求出△EBF的周长为8cm.

结语

初中数学解题能力培养可以通过对原题进行思考，探索其所考的知识点及系统的知识框架，通过拓展原题或者延伸相类似的知识点，去形成系统性和条理性的解题思路，使得解题思路更加灵活.本文以两个几何例题进行探究和分析，并对两个例题进行拓展，进而培养学生的解题思路，使学生对问题有更深入的理解，能够灵活应变地做一类题而不是某一道题.此外，通过在思考中探索、在拓展中创新的方式培养数学解题能力，增强学生的问题意识和探索精神，培养学习兴趣和自信心，为他们的数学学习和综合素质发展奠定坚实基础，并为未来的学习和职业发展打下良好基础.

参考文献：

［1］孔婷薇.初中数学学生解题能力的培养研究［J］.数学学习与研究，2023（08）：146-148.

［2］李权生.初中数学教学中如何培养学生的解题能力［J］.新课程，2022（11）：156-157.

［3］阮准.初中数学解题反思能力的培养［J］.数理化解题研究，2022（26）：41-43.