简单问题复杂化，锻炼学生发散思维

【摘要】初中数学教学越来越注重学生思维能力的培养和创新意识的激发.通过对基础数学问题的拓展和深化，不仅能够锻炼学生的思维发散

能力，还能激发他们对数学学科的兴趣和探索欲望.本文从初中数学一道几何习题的解答出发，探讨“一题多解”策略在教学中的应用.

【关键词】初中数学；发散思维；一题多解

1 引言

一题多解就是将简单问题复杂化的重要方式，通过鼓励学生从不同角度审视问题，运用所学知识进行创新性解答，进而提升其解决复杂问题的能力.

2 试题呈现

如图1所示，大小两个正方形水平紧靠放置，请用尽可能多的方法，求阴影部分面积.

3 思路分析

本题为典型的小初衔接阶段的几何题目，其解法有很多.第一，可将不规则的图形划分为两个或多个规则图形进行求解；第二，若空白部分面积可求，则可将不规则图形置于规则图形内，通过规则图形面积减去空白部分面积即可求出.

进入初中阶段，随着学生所掌握知识点的增加，该题也具备了一些拓展方式，例如“三角函数”“相似三角形”“割补法”等解题模型.

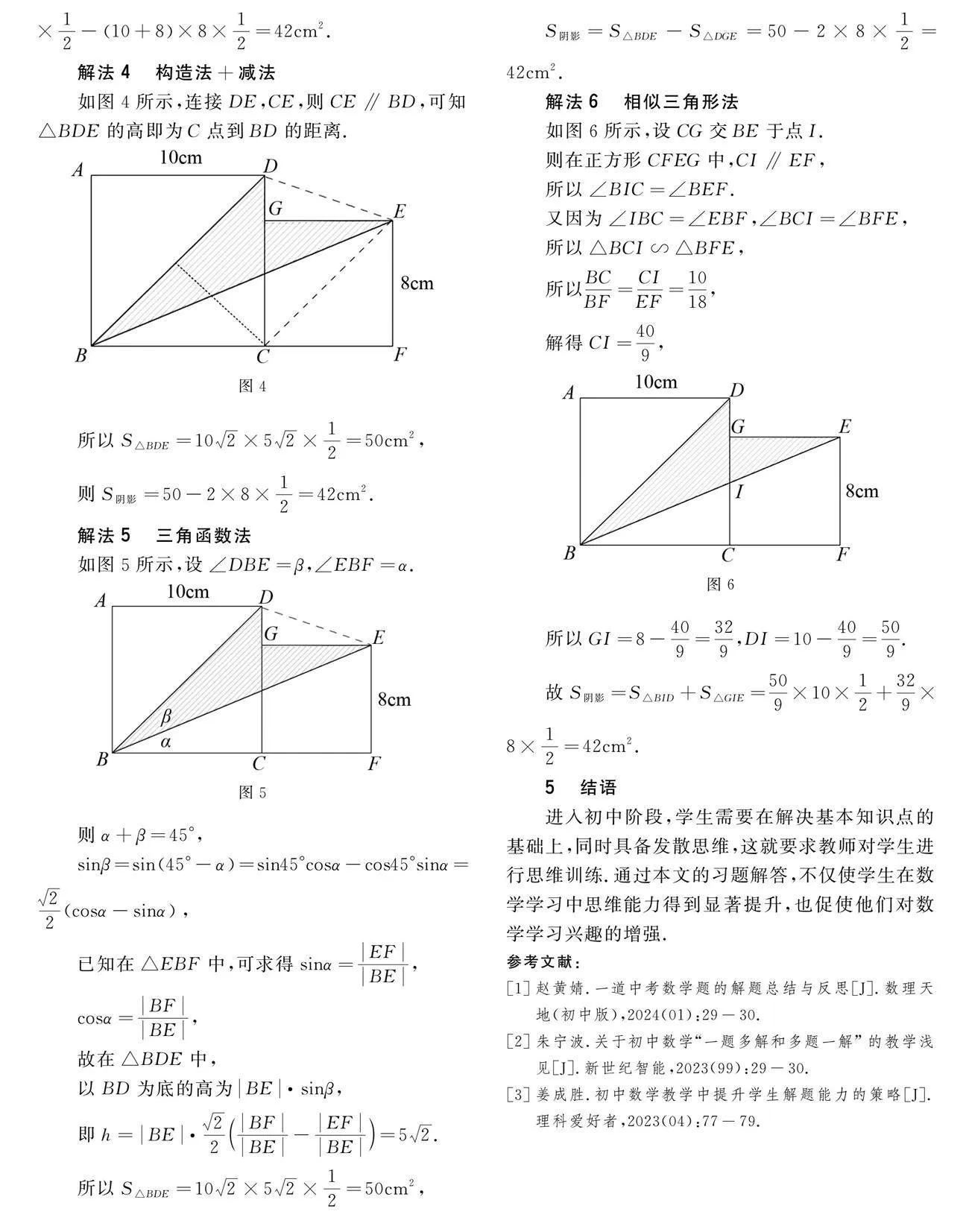
4 解法探究

解法1 直接构造法

如图2，连接BG，则S阴影=S△BGD+S△BGE.

5 结语

进入初中阶段，学生需要在解决基本知识点的基础上，同时具备发散思维，这就要求教师对学生进行思维训练.通过本文的习题解答，不仅使学生在数学学习中思维能力得到显著提升，也促使他们对数学学习兴趣的增强.

参考文献：

［1］赵黄婧.一道中考数学题的解题总结与反思［J］.数理天地（初中版），2024（01）：29-30.

［2］朱宁波.关于初中数学“一题多解和多题一解”的教学浅见［J］.新世纪智能，2023（99）：29-30.

［3］姜成胜.初中数学教学中提升学生解题能力的策略［J］.理科爱好者，2023（04）：77-79.