探索核心素养背景下渗透模型思想的方法

[摘 要] 核心素养背景下的数学教学需关注模型思想的渗透. 文章以模型思想的概述为起点，分别从定理教学、试题探索、案例示范三个方面对模型思想的渗透方法展开例析，并从方向明确、方法得当、适当实施三个角度谈一些思考与感悟.

[关键词] 模型思想;核心素养;定理

有数学家认为，学生在学校所学的知识到工作中用到的并不多，但学习过程中深入内心的思维方式、思想方法、数学精神、推理能力或研究问题的视角等，却会长久地发挥作用，令学习者受益终身[1]. 随着新课改的推进，模型思想被列入核心素养的范畴，如何在初中数学教学中渗透模型思想呢？实践证明，依靠几种几何模型或应用题远远达不到预期效果，反而会局限学生的思维，让学生觉得只有提到“模型”或“应用”等词汇才属于模型思想. 殊不知，模型思想有着更广泛的定义.

模型思想的概述

模型思想是指有意识地应用数学原理或方法来理解或解决实际问题的思想，紧扣客观对象的本质特征，用恰当的数学语言进行表征的过程. 从狭义的角度来看，模型思想就是解决客观问题的思想方法，如方程、函数、不等式等模型就是联系数学学科与生活实际的纽带. 由广义的视角来分析，引导学生用数学思维思考并解决实际问题是模型思想的本质. 不论是概念教学，还是用复杂的知识解决综合性问题，都是培养模型思想的契机.

值得注意的是模型思想与数学建模并不是一回事，模型思想属于从广义的角度研究数学问题，而数学建模则属于狭义的范畴. 事实上，核心素养背景下的数学教学，更需从广义的角度来探索蕴含丰富内涵的模型思想，这是促使学生形成关键性人格品质的主要途径.

渗透模型思想的措施

1. 模型思想渗透在定理教学中

案例 “圆周角定理”的教学

师：如图1，∠AOB与∠ACB所对的弧为同一条，请分别测量出弧AB所对的两个角的度数，分析它们之间存在怎样的关系.

生1：测得∠AOB与∠ACB的度数分别为110°与55°，110°恰好为55°的2倍.

师：这个结论是否适用于所有情况呢？现在请大家自主画一个任意圆，并从中取任意一段弧，分析这段弧所对的圆心角与圆周角的度数关系.

学生自主画图并测量，很快就获得结论：在任意圆中，同一段圆弧所对的圆心角的度数为圆周角的2倍.

师：为了进一步验证该结论是否正确，现在请大家来看计算机的演示：借助几何画板以动画演示的方法分别测量∠AOB与∠ACB的度数，要求学生通过观察分析圆心角与圆周角的度数关系.

生2：我发现不论所取的弧在什么位置，∠AOB始终为∠ACB的2倍.

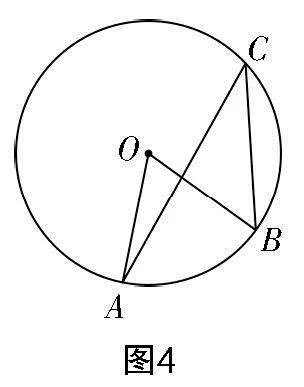
师：通过这个证明，可确定圆心处于圆周角的边上位置时，猜想是成立的. 那么关于图3与图4的情况，猜想是否依然成立呢. 请以小组合作的方式来探索.

生4：既然我们已经探索了圆心处于圆周角边上的情况，那么借助辅助线CD，可将问题转化成类似于图2的情况（见图5），由此可直接获得∠AOD=2∠ACD与∠BOD=2∠BCD，所以∠AOB=2∠ACB.

师：上述证明方法应用了迁移与转化的过程. 还有其他方法吗？

生5：若在图4中作CD这条辅助线可得图6，也就是将图形转化成了大家所熟悉的图2，结论也就浮出水面.

分析 此教学片段，学生所提炼到的模型思想为：把圆心处于圆周角的内部、外部，转化成圆心处于圆周角的一边上进行探索与研究. 观察此教学片段的明线，学生主要亲历了用数学符号语言来描述数学问题数量关系的过程;基于教学暗线分析，此环节将模型思想贯穿始终，主要体现在“提出问题—建立模型—分析与应用”方面.

2. 模型思想渗透在案例示范过程中

案例2 “反比例函数”的探索

点P（2，2.5），S的值是多少？③如图10，若点P（-2，-2.5），S的值是多少？

通过对以上问题的探索，根据相关因素假设与分析初步形成模型Ⅰ，即S与k的数量关系为______.

通过对以上问题的探索，根据相关因素假设与分析初步形成模型Ⅱ，即S与k的数量关系为______.

基于以上结论，进行验证（略）.

模型的应用：

△ABO的面积.

分析 以开门见山的方式展开探索，学生在问题情境的研究与思考中抽象出基本模型. 其中，问题串的应用成功将静态的知识动态化，让学生由图象出发，对这部分内容由感性认识逐渐转化为理性认识. 循序渐进的问题是为提炼模型所设定的小目标，解决问题的过程不仅让学生感知了坐标与线段长的关系、S与k的关系，还促使学生自主类比、猜想、思考，从而抽象出相应的模型，验证与应用模型是感性认识上升到理性理解的过程，学生在此过程中提升了模型意识.

关于渗透模型思想的几点思考

1. 方向明确

当前的数学课堂教学更注重学生的主体性地位. 教师作为课堂的组织者，需引导学生亲历实际问题转化为模型的过程，并鼓励学生自主计算并检验结论，为改善教学方法提供参考依据. 因此，作为具体执教的数学教师需明确教学方向，引导学生在充分理解数学的基础上，为后续学习更多复杂的内容夯实思维与方法基础.

当遇到一个问题时，学生必须有明确的思考方向，明白哪里是思维的起点，该朝什么方向去分析，通过问题的解决逐步建立学习信心. 一旦师生都有明确的“教与学”的方向，并以积极互动的模式加强探索与分析，必然能有效增强学生学习的主动性，拔高学生的思维，帮助学生成功建立模型思想，最终实现教学相长.

2. 方法得当

数学学习并不仅仅局限于将实际生活问题转化为专业的数学问题那么简单，更重要的是引导学生学会用数学的眼光观察现实世界，用数学的思维来思考现实世界，鼓励学生学会提炼学习方法与数学思想，让学生感知不同模型可以用来解决同一个现实问题，同时，同一个模型又能用来解决各类不同的现实问题. 学生一旦明确了这一点，自然而然地会对数学模型产生浓厚的兴趣.

为了培养学生的数学模型思想，还可以创设一些数学建模比赛，激发学生的潜能，鼓励学生在自主探索中提升学力，以真正发展学生的“四基与四能”，提升学生的“三会”能力，让核心素养落地生根.

3. 适度实施

没有一门学科是独立存在的个体，学科与学科之间多多少少有一些联系，正是这种关联催生了丰富多彩的世界. 模型思想的渗透同样需从跨学科的角度来整合学生的思维，引发学生的合作意识[2]，并通过文献资料的查阅与信息的收集等，不断提升学生的能力.

值得注意的是课堂中渗透数学模型思想，需关注对学生思维广泛性、灵活性、容错性的培养，但初中阶段的学生受认知水平的限制，在这一方面还有所欠缺，而学生的时间又是有限的，因此教师要杜绝将模型思想的渗透等同于建模活动要求，因为对学生提出过高要求反而会消减学生学习的积极性，得不偿失. 事实证明，根据学生的实际认知发展水平适度渗透模型思想是拔高学生数学思维，激发学生创新意识的重要举措.

参考文献：

[1]邵光华. 作为教育任务的数学思想与方法[M]. 上海：上海教育出版社，2009.

[2]曹培英. 数学基本思想与学科核心素养[J]. 教育研究与评论（中学教育教学版），2016 （10）：91-92.