数学微型探究活动存在的问题与应对措施的研究

[摘 要] 微型探究活动的开展，可进一步深化学生对知识重点、难点的理解，培养学生的数学意识. 实践中，数学微型探究存在如下几类问题：学情掌握不准、要素配置错位、难易程度失控、活动设计失当、探究方法失调. 为此，研究者借助几个教学实例分别针对每一种情况，谈一些应对措施与思考.

[关键词] 微型探究;活动;学情

数学微型探究活动是指根据学情与教学内容的特点，择取一个合适的角度，围绕教学重点与难点开展短时间的探究活动，能为学生创造探究机会，形成活动体验. 这种探究活动属于定向探究类型，需结合学生的实际需求与教师的教学经验设计教学活动，活动以用时短、切口小、符合实际、灵活等为特点. 这种探究活动的开展，可进一步深化学生对知识重点、难点的理解，培养学生的数学意识. 方法虽好，但实际实践中仍存在一些问题，本文将每一种问题罗列出来，并借助实例谈一些应对措施与思考.

学情掌握不准

学情诊断是设计教学方案的首要步骤，教师若无法精准掌握学情，那么设计的教学方案则有可能偏离学生的认知区域，导致教学的失败. 传统的学情诊断以发放学案或访谈为主，这种方法搜集学情费时费力，而且还会出现判断失误的现象. 甚至有些老师在设计教学活动之前，完全凭借自身的经验来判断学情，这种脱离课程标准与教材要求的做法，会让教师对学情产生失察现象，致使不少学生难以全身心地参与到微型探究活动中来.

事实证明，新课标引领下的数学学情诊断，可借助信息技术手段，如极课大数据的应用，从学生的作业、练习训练中提取数据，精准判断学情，为教学做准备.

案例1 “二次函数与一元二次方程”的教学.

例题教学完毕后，为了进一步巩固学生对教学重点与难点的理解，教师设计了如下问题：若二次函数y=x2+2ax+b2与y=x2+2bx+c2的图象和坐标横轴存在两个不重合的交点，函数y=x2+2cx+a2的图象和坐标横轴相交吗？说明理由.

本节课教学重点与难点在于探索二次函数图象和一元二次方程根之间存在怎样的关系. 因为学生所接触的二次函数以数字系数的二次函数为主，本例显然超出了常规范围，三个带字母系数的二次函数让大部分学生感到束手无策，同时此问也超出了课标要求，缺乏探索意义.

案例2 “直线与圆的位置关系”的教学.

问题 如图1，已知矩形ABCD中，AB=20 cm，BC=4 cm，若点M以4 cm/s的速度由点A开始，沿着A，B，C，D进行有序运动，点N则以1 cm/s的速度由点C处开始，沿着CD边进行运动，若点M，N分别从点A，C同时出发，在点M，N中的一个点抵达点D时，另一个点立即静止不动. 若圆M，N的半径均为2 cm，求点M在运动多久时，圆M、N间仅有一个交点？

分析 此例是结合教学内容特点与学生实际情况而编制的一道微型探究活动题. 题的背景为两个动态变化的圆，这就给学生的理解带来了较大的障碍，关于两个圆仅有一个切点的问题，大部分学生可以理解，但关于两个圆的变化过程，却让不少学生感到棘手. 本题两个圆在运动过程中存在三次只有一个交点（外切）的情况，想要从真正意义上探索这两个圆的关系，着重在于探索两个圆心在运动时存在什么样的关系. 显然，这超出了学生的认知范畴，导致学生难以理解. 因此，本题也是在没有精准把握学情的基础上所设计的，探究活动缺乏可行性.

类比两个案例，不难发现微型探究活动的设计离不开对学情的精准诊断. 若教师完全不顾及课标要求、教学内容的特点以及学生的实际认知水平，仅凭自己的经验设计微型探究活动，则会让探究内容变得过深、过宽，拉大学生与问题之间的差距，探究活动也因此难以达成预期的目的，更有甚者还产生负面影响.

想要从根本上规避这个问题，最好的方法就是择取适切的探究活动内容. 如案例1的探索，可通过对数字系数的减少来设计活动;案例2则可将探究问题更换成“两圆在直线上运动”. 同时，教师作为课堂的引导者，需时刻关注学生在探索过程中的情况，必要时可为学生的思维搭建“脚手架”，让学生有明确的思考方向. 若学生表现出探索困难，教师还可借助课堂交流的模式启发学生的思维，让学生在师生、生生积极的互动中提升探索效率.

要素配置错位

数学微型探究活动的设计涵盖了问题背景、知识内容、活动程序、思维空间等诸多要素，这些要素均在教学目标的统领下互相调适、配合. 然而，实践发现，有些教师设计微型探究活动会忽略这些要素的关联性，常因配置错位而导致探究活动偏离教学目标的情况发生，这种虚化教学目标，弱化教学成效的设计方案，值得每一个教师去关注与思考.

案例3 “用二元一次方程组解决问题”的教学.

教师为了帮助学生更好地理解用二元一次方程组解决实际问题，有针对性地设计了如下微型实验探究活动.

活动1 分别取10枚一元硬币与10枚五角硬币，按照币值分成两摞重叠摆放，用刻度尺分别测得两摞硬币的厚度;而后用天平分别称出这两摞硬币的质量，同时计算每一枚一元与五角硬币的质量是多少.

活动2 将一些一元与五角的硬币混合并叠放在一起，用刻度尺测量出厚度，并称出所有硬币的质量，借助二元一次方程组获得两种硬币的个数，算出总金额.

活动3 以小组为单位，提一些与硬币活动相类似的问题，并借助二元一次方程组来解决所提出的问题.

二元一次方程组是初一年级所接触的内容，而用天平称重却要到初二年级才有所涉及. 以上活动需要应用到天平称重这一操作，因此教师需先教会学生如何正确使用天平，显然这个过程偏离了本节课教学的主题. 此活动，教师若直接将硬币的厚度与质量呈现给学生，未尝不可.

微型探究活动的开展需紧扣教学目标来设计，要杜绝为了加强数学实验机会，而不管教学需求就盲目地添加操作活动，致使解决问题的过程严重偏离教学主题，浪费宝贵的课堂时间. 想要避免此类要素配置错位的问题，教师在设计教学活动时就要以教学目标作为出发点，提前预测课堂中可能会出现的问题，将各种不匹配的因素逐一转化、化解.

如本例，教师需明确认识到天平称物为本节课的辅助活动，教师可直接给出具体数据，或自主动手操作，也可以指派一个动手能力较强的学生进行操作.

难易程度失控

微型探究活动离不开问题的引导，而问题的难易程度又决定了探究的质量. 有些教师在设计问题时，没有考虑到学生的实际认知水平，试图通过一定难度的问题拔高学生的思维，殊不知，难度过大的问题会严重消减学生的探究信心，阻碍学生的探究步伐;还有些教师为了让所有学生都能积极地参与到探究活动中，设置过于简单的问题，导致学生体会不到探究带来的挑战性与成就感. 因此，过难或过于简单的问题都不利于学生思维的成长.

案例4 “勾股定理的逆定理”的教学.

问题1 勾股数有很多组，你们能列举100组吗？

学生虽然能说出一部分，但受课堂时间与学生认知的局限，无法在短时间内列举100组勾股数. 为此，教师为学生的思维搭建了如下平台.

问题2 若m，n为正整数，（m2+n2）2-（m2-n2）2=（2mn）2，让c=m2+n2，a=m2-n2，b=2mn，据此可写出几组勾股数？

观察本例，第一个问题要求学生说出的勾股pfqIbsh+ssxEJiit52PJE0s+9uSeccKBi7M4XIJtdSQ=数组的量过大，显然超出了课堂基本思维容量，学生也难以从中探寻出一般规律;第二个问题虽然降低了难度系数，但教师直接将公式（m2+n2）2-（m2-n2）2=（2mn）2提供给学生，导致问题没有难度可言，那就丧失探究的意义. 其实，第二问中的公式对学生而言是一个具有探究价值的内容.

另外，通过本题教师还可以带领学生从a2+b2=c2着手，借助a2=（b+c）（b-c），让b-c=1，仅需b+c为一个完全平方数，则可构造出无数组勾股数. 想要把握好探究问题的难易程度，离不开对学生实际认知水平的判断与探究课题的遴选，适切的探究活动才能达到预期的目标.

活动设计失当

微型探究活动同样需要经历实验操作、观察等步骤，那么在设计活动方案时，则需要思考如下几个问题：与微型探究相关的活动有哪些;各项活动需满足什么要求;怎样调控活动过程;如何应用活动结论等. 若考虑不周，很有可能会影响探究成效.

案例5 “平面图形的认识”的教学

授完第一节课后，教师要求学生自制测风仪，具体要求为：将一张画有量角器的纸张剪贴在硬纸板上，并在量角器的中心打孔、穿线，线的另一端系上乒乓球. 第二节课上，教师要求学生利用自制的测风仪对着电风扇吹，同时记录细线偏离铅垂线的角度数据，对照教师所提供的“风速对照表”来测量风速.

学生自主操作，结果因自制的测风仪没有充分考虑到材料规格、工艺等要求，导致操作时角度和风速与对照表出现了不匹配的情况，其主要原因是自制的测风仪过于简陋，无法应用风速对照表. 其实，这是一个很有意义的探究活动，但因为教师在工具设计指导上没有考虑周全，导致探究活动无法发挥其应有的价值.

回顾这个探究活动，学生费时费力地自制测风仪，对课堂本充满期待，但在实际应用时却宣告失败，这严重挫伤了学生的积极性. 活动应从求简的角度进行改进，如教师为学生提供制作材料，鼓励学生以小组合作的方式制作测风仪，将测风速更换为在同一风速下，不同角度风速大小的探索，引导学生建立角度与风速呈大致对应的模型，可成功激发学生的探索欲，显著提高探究实效.

探究方法失调

开展微型探究活动的主要目的在于引导学生经历知识的发生、发展过程，感悟并理解知识的应用，获得分析问题与解决问题的能力. 然而，实践中有些教师只关注探究活动本身的设计，忽略数学思想方法的铺垫，这种探究方法的失调难以从真正意义上发挥微型探究活动应有的价值.

案例6 “平行四边形”的教学

当学生对平行四边形的定义、性质等有所了解后，则进入思维拓展环节，为了进一步激活思维，一位教师设计了如下问题：

请用圆规在图2上画一个点P，让点P位于AB的延长线上，并满足PB=AB.

这是一个应用指定工具画图的问题，从学生已有的认知出发，仅有圆规难以获得满足题设条件的线段，因此很多学生看到这个问题都束手无策.

此探究活动的失败，主要原因在于缺少了探究方法的铺垫. 该探究活动首先需考虑的问题是圆规能构造出哪些图形.

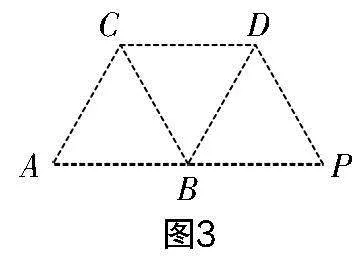
此问中，用圆规可以分别作出点C、D，让△ABC与△DCB全等. 如图3，四边形ABDC为平行四边形，同理构造平行四边形PDCB.

综上分析，本例可增加两个问题作为学生思维“脚手架”：①用圆规在图2中作点C，让△ABC为等腰三角形;②继续用圆规作点D，让四边形ABDC为平行四边形. 在这两个问题的点拨下，学生则能顺利解决问题.

实践证明，微型探究活动的方法中常蕴含了丰富的数学知识与思想，教师在设计探究活动时应考虑到这条暗线，对探究活动涉及的通性通法、数学思想、特殊方法等，做到心中有数，必要时借助一些小问题为学生的思维搭建台阶，让学生在知识与方法的类比迁移中探寻数学本质.

总之，微型探究活动的开展既离不开对学情的精准诊断，又离不开教师的精心筹划与判断. 这也对教师的业务水平提出了更高要求，教师应将发展学力作为探究活动设计的载体，让微型探究活动发挥其应用的价值.