指向深度学习的初中数学作业设计研究

[摘 要] 作业是教学活动中不可或缺的重要组成部分. 研究者从指向深度学习的作业设计理念出发，以“图形的轴对称”作业设计为例，分别基于夯实基础、提升能力、发展素养、整理复盘四个层次设计对应的作业内容，并谈一些思考.

[关键词] 深度学习;作业设计;轴对称

数学作业设计是指教师结合课标要求、教学目标、学情等，针对具体教学内容，以自主开发、重组、改编等手段，为学生量身定制的任务活动. 教师通过学生作业反馈情况可对教学目标与素养的达成进行客观评价，同时，作业也是教师调整与改进教学方案的重要依据.

指向深度学习的作业设计理念

深度学习是指围绕具有一定挑战性的学习主题，学生积极参与活动过程，感知并体验成功，从中获得发展的有意义学习过程，此过程包含核心知识、问题解决、思维发展、团队合作、有效沟通等维度的内容. 其中，“挑战性的学习主题”体现在学生对知识的认知层次与关联知识内在结构的研究内容上.

深度学习的关键在于引导学生深度参与学习过程，目的为促使学生思维的有效发展. 指向深度学习的作业设计是指以促进学生的深度学习为主要目的，促使学生从本质上理解教学内容，掌握各个知识点之间的联系，并能够批判性地加以应用，在有效沟通与迁移中解决问题，拔高思维，发展数学核心素养.

Om68UKTN8mPDsgA+Rbt3cg==案例设计与说明

关于“图形的轴对称”课后作业的设计，教师结合学情、教情与考情特点，由浅入深地设置了四组作业，以满足不同认知水平层次学生的实际需求，让每个学生都有作业可做，并能在作业中获得不同程度的发展.

A组：夯实基础

1.观察如下几幅图形，属于轴对称图形的是（ ）

2. 五角星有（ ）条对称轴.

A. 1条 B. 3条

C. 5条 D. 无数条

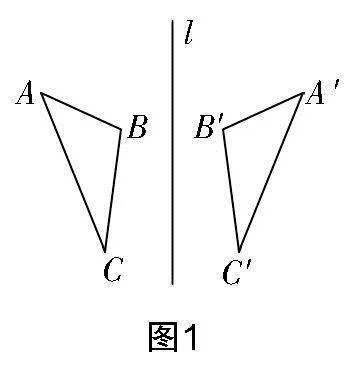
3. 如图1，已知△ABC与△A′B′C′关于直线l对称，如下结论正确的有（ ）

①∠ABC=∠A′B′C′;

②△ABC≌△A′B′C′;

③l为线段CC′的垂直平分线;

④直线BC与B′C′的交点不一定位于l上.

A. 1个 B. 2个 C. 3个 D.4个

4. 如图2，直线AC为轴对称四边形ABCD的对称轴，已知∠B=40°，∠DAB=150°，那么∠BCD=______.

5. 如图3，已知四边形ABCD是边长为6的正方形，那么阴影部分的面积是______.

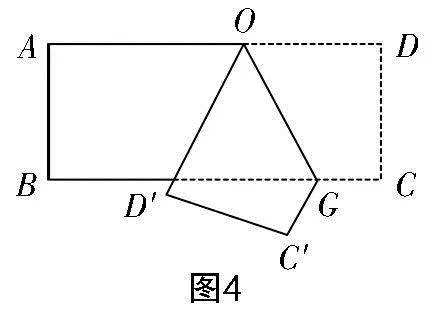
6. 如图4，将一张长方形的纸以图示方式折叠，使得点C，D分别落于点C′，D′处，当∠OGC′=125°时，∠AOD′=______.

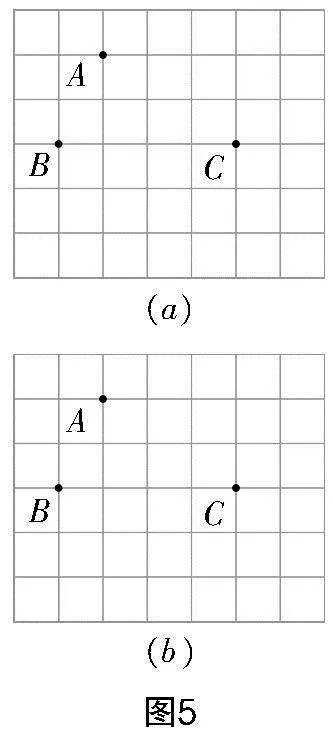
7. 图5为两幅完全一样的正方形网格图，点A，B，C分别位于格点上，请分别在两张网格图中寻找不同位置的点D，使得四边形ABCD为轴对称图形，并将对称轴标注出来.

设计说明 A组练习为一组基础题，意在响应新课标的要求，让人人都能在数学学习中获得不同程度的发展. 这组作业难度较小，每个水平层次的学生都能解决，以激趣、调动学习积极性为主，因此这是一组面向全员的练习，旨在让学生通过基础练习，夯实基础知识，建立学习信心.

B组：提升能力

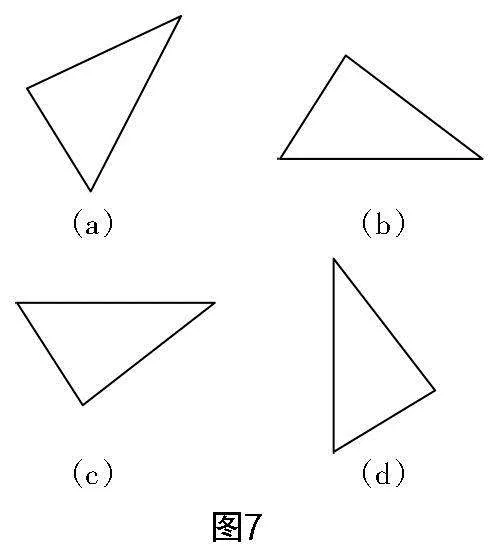
8. 变换图6中的△ABC，获得图7中的图，其中以轴对称变换而来的是（ ）

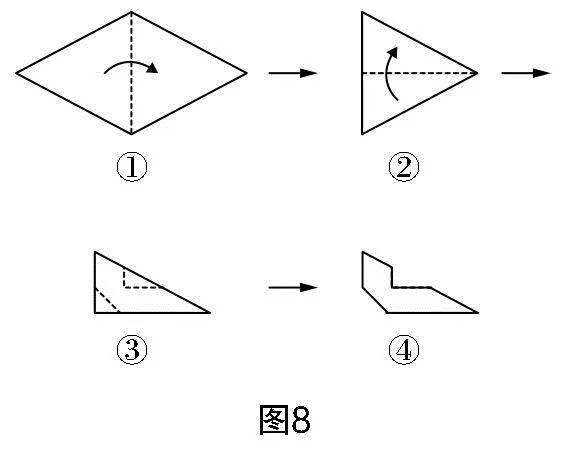
9. 剪纸是大家所熟悉的一种民间艺术. 如图8，将纸沿着图①②的虚线进行折叠，沿着图③的虚线剪裁，打开图④，所获得的图案为（ ）

10. 如图9，在正方形网格中，△ABC的顶点均位于格点上，已知△DEF与△ABC关于某直线成轴对称图形，请分别在网格中画出六种位置不一样的△DEF.

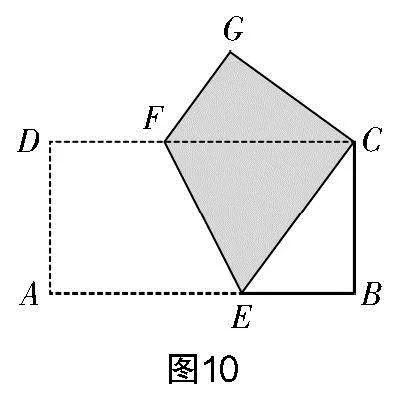
11. 如图10，若将长方形ABCD沿着EF进行折叠，让点A，C重合，让点D落于点G处.

（1）证明：△GCF≌△BCE;

（2）如果AB为8，AD为4，那么四边形CGFE的面积是多少？

设计意图 想要在作业中促进深度学习的发生，就要让学生的思维逐渐“深”下去，并“晕染”开来. 这就需要从学生的知识与技能、思维水平、能力以及人格品质等方面着手，让学生成为一个全面发展的人. B组练习设计意在引发学生的自主探究，以揭露概念的本质，提升学力.

这几个问题由浅入深，既有深度，又有宽度. 如第8题，学生想从各种图形中发现轴对称图形，就要对轴对称图形的概念有深刻理解;第9题则需在“做中学”，这是揭露对称问题本质的重要过程;第10题属于开放性设计题，可进一步发散学生的思维;第11题需学生从几何直观出发，逐渐过渡到理性推理，让学生充分体会知识的应用价值.

纵观B组的这几道题，着重在于引导学生从不同的视角来感知轴对称的本质，并在比较与分析中深化理解，让思维变得更加深刻.

C组：发展素养

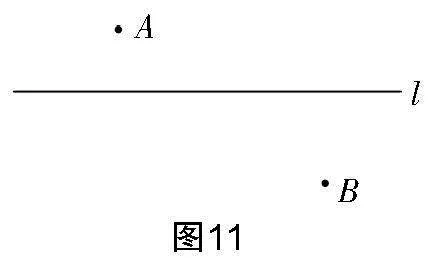
12. （1）如图11，若直线l代表了草原上的一条河流，一位将军从点A处出发到河边饮马，而后到点B处工作，他怎样行走路程最短？请在忽略河宽的情况下作出最短路线.

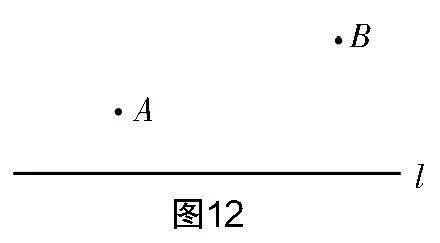
（2）如图12，若直线l表示河流（忽略河宽），将军从点A出发到河边饮马，而后到点B处工作，怎样行走路程最短？请在图中标注.

（3）如图13，草地用直线a表示，河流为直线l，若从点A出发前往草地放牧，而后到河边饮马，之后再到点B处，如何行走可让路程最短？请在图中画出来.

13. 如图14，已知四边形ABCD中的∠B，∠D为直角，∠C=58°，AB=3，AD=4，点E，F分别为BC及DC边的动点，当△AEF的周长处于最小值时，∠FAE的度数是多少？

设计说明 这组作业意在让学生感知知识的发生与发展历程，领悟其本质，发展关键能力，以促进数学思维的生长，为发展数学核心素养奠定基础. 图形的轴对称问题对发展模型观念具有重要价值，以作业的方式引导学生从复杂的情境中提炼数学思想，可增强学生的实际应用能力. 如第12题，学生在三个问题的启发下，有效训练了思维的完整性，并在类比分析中领悟概念本质，对轴对称建立模型，从真正意义上实现了深度学习.

D组：整理复盘

要求学生以思维导图的方式将与图形轴对称相关内容梳理到一起，形成完整的知识架构，完善认知结构的同时提炼学习方法.

设计说明 新课改背景下的作业不能将学生框死在做题上，而应鼓励学生学会总结与反思，形成整理能力，这是深度学习理念下，学生应具备的能力.

几点思考

1. 注重基础，练得实

巩固基础知识，培养学生的数学学力，发展核心素养是作业设计的主要目的，所以作业设计不能毫无选择地应用教辅资料，更不能以“炒冷饭”“复制粘贴”的机械训练糊弄过去，那样不仅不能锻炼学生的思维，还会消减学生的探索欲，导致学生对学习丧失信心. 立足于新课标的要求，设计具有激趣启思的作业，可从教材例题、经典例题变式、不同层次与不同角度出发，这对提升学生的理解与应用能力具有重要影响，学生在具有丰富内涵的作业训练中不仅能练得实，实现深度学习，还能发展学力.

如本例中的A组题，则从轴对称的概念、判断、对称轴的性质、作图、应用等角度，引导学生全方位认识并理解图形的轴对称特征. 学生在系统、全面的练习训练中，亲历知识生长过程，牢固知识体系，这种精准扎实、有的放矢的基础练习是深度学习的基础，也是发展学力的关键.

2. 关注联系，研得深

想要让深度学习发生，必然要“研得深”，作业是践行深度学习的基本载体，设计时需响应新课标的“以生为本”的理念，带领学生在理解与巩固知识的基础上感知知识的渐进性、开放性与关联性特征. 为此，作业设计应从知识的发生、发展、前后逻辑关系、知识的关联度等方面着手，让学生能在作业中构建良好的框架，完善知识体系，拔高思维.

如B组练习，根据教学内容的特点与学生认知水平的实际情况分别设计了开放发散性、实践应用性以及逆向思维性的问题，成功吸引了学生的注意力，让学生自主进入深入探索状态，并在问题的解决中获得用所学知识解决实际问题的能力.

3. 落实素养，悟得透

教师不仅要从结果去评价学生的学习，还要从过程去分析学生的学习，关注“过程”的评价方式可进一步激励学生的学习，当然，这也是教师调整或改进教学策略的依据. 作业设计同样不能只关注作业结果，还要注重学生作业完成过程中形成的感悟、思想与能力等. 将知识难点或学生理解困难的一些问题归类到一起，设计成层次分明的练习，可促使学生更好地理解与感悟知识重点与难点，这是提升数学思维，让学生“悟得透”的重要方法之一.

如12题为著名的“将军饮马”问题，前两个小题学生比较容易理解，应用轴对称知识就能解决，但第（3）小题与13题则较复杂，需要学生在熟知轴对称性质后，才能获得结论，这给很多学生带来了较大的挑战. 12题的前两个问题为后面复杂的问题奠定了基础，让学生的思维在问题的启发下逐渐深刻. 因此，教师在设计作业时，可将一些学生理解困难的问题逐层延伸、变形后组合在一个题中，让学生亲历思考与感悟的过程，充分理解知识本质，发展数学思维，提升综合素养.

4. 整理反思，理得清

习惯的培养是教育的重要任务之一. 作业设计需将学生个体的长期可持续性发展作为重要目标，深度学习理念下的数学教学更关注对学生数学品格的培养. 同样，作业设计也应关注对学生能力与习惯的培育，如让学生在作业中学会自主总结、归纳、反思、复盘等，这些都是健全人格品质的基础.

如本例最后一项作业，要求学生将所学知识、方法等用思维导图的方式进行梳理与展示，就是让学生通过作业学会整理与反思. 学生在这一类作业的引导下，往往能有效促进核心素养的发展.