关注数学理解 提升数学素养

[摘 要] 新课标背景下，初中数学教学越来越关注对学生综合能力和综合素养的培养. 为了达到这一要求，教师应从学生实际学情出发，创设贴近学生实际的探究活动，以此激发学生的探究欲，让学生更好地体验与理解、思考与探索知识，进而实现对知识的融会贯通，切实提高发现、分析和解决问题的能力，发展学生数学核心素养.

[关键词] 数学理解;数学核心素养;初中数学

问题的提出

无理数是数的又一次扩充，引进无理数对数学的发展有着重要意义. 相对于有理数，无理数更加抽象，其中隐含的“无限”“不循环”给学生的理解带来了困难. 为了让学生理解和接受无理数，应该让学生感受无理数逻辑上的合理性.

在无理数概念教学中，首先从开方开始，即“如果a2=2，则a是多少”. 教材中采用“二分法”逐步推导，确定a的个位、十分位、百分位……，从而得到a是一个无限不循环小数[1]. 这样做的优点是可以将前后知识联系起来，但是其不足是学生容易产生错觉，认为无理数就是开方开不尽的数，可见通过经历以上过程，学生虽然知道无理数的概念，但是并不能让学生真正地理解和接受无理数的概念.

教材中给出以上推理过程，其目的是让学生更好地接受无理数. 不过从教学反馈来看，大多数学生虽然能够看得懂，但是却不能独立完成证明. 很多学生的证明过程推理模糊，缺乏条理性，而逻辑论证对无理数概念的建立有着不容忽视的作用，为了让学生更好地理解和接受无理数逻辑上的合理性，笔者尝试采用一种图形证法，以此借助图形的直观帮助学生理解这个命题及其证明，发展学生逻辑推理素养.

教学过程

1. 操作与思考

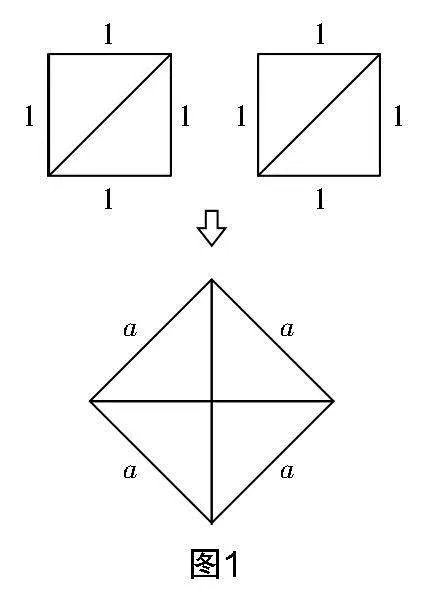
问题1：如图1，现有两个边长为1的小正方形，将其沿对角线剪开，得到一个大正方形，大正方形的边长是多少？

2. 操作与推理

教师给出假设后，通过创设问题引导学生主动参与推理，过程如下.

问题2：如图2，现有两张边长为n的小正方形纸片，面积记为S，若将两个小正方形纸片拼成一个正方形，则可以得到一个边长为m的大正方形，大正方形的面积记为S. 由此你能得到怎样的数量关系？

学生活动：结合已知易得S=2S，即2n2=m2.

问题3：如图3，将其中一个小正方形移到大正方形中，两个正方形未重叠部分的面积记作S′1，由此你能得到怎么的数量关系？

学生活动：学生通过观察、推理，易知S=S′.

问题4：如图4，在原有的基础上，将另一个小正方形也放到大正方形中，你有哪些发现？

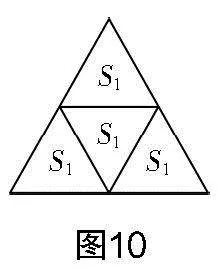
学生活动：根据图形对称性可知，两个小正方形重叠部分为正方形，其边长为2n-m，面积记为S;未重叠部分的两个小正方形边长为m-n，面积记为S;余下两个L型图形全等，其面积记为S′，则S+S′=S+S′+S，即S=2S.

问题5：如图5，若将得到的两个面积为S的小正方形平移到S中，你又有什么发现？

学生活动：学生结合图5及以上探究经验，得到S=2S .

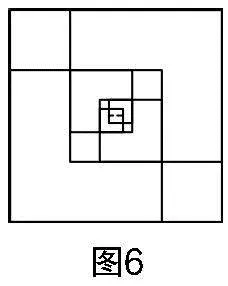
问题6：如图6，如果按照以上步骤继续操作下去，你还能得到怎样的数量关系？

学生活动：学生结合以上规律，又得到S=2S，S=2S……

问题7：已知m、n是正整数，由此你能得到什么？

师生活动：学生先独立思考，教师给予适时指导，学生通过合作探究得到正方形S、S、S……的边长都是正整数.

问题8：如图6，正方形在不断变小，这样正方形的边长也会bW60XynsR9spzj1+pozt5LxndM2pXmO7Ti63My9LIxE=不断减小，那么正方形的边长是整数，成立吗？

设计意图 教学中，教师巧妙地结合图形让学生操作、观察、联想、验证，由此发现若假设成立，则小正方形的边长均为正整数，但是根据“最小数原理”，若按照以上过程无限迭代下去，必然会存在正方形的边长小于1的情况，由此借助图形完成证明. 在此过程中，教师预留时间让学生观察、推理，有利于激发学生的主体性，培养学生逻辑推理能力.

3. 操作与推广

设计意图 通过适度的拓展延伸，帮助学生跳出图形只能是正方形的局限，拓宽学生的视野. 同时，在此过程中，教师将探究的主动权交给学生，这样一方面可以检测学生对该图形证法的掌握情况，另一方面可以借助几何直观，培养学生逻辑推理能力.

设计意图 经历以上证明过程不仅可以进一步强化已有知识方法的理解，而且通过有效对比，可以让学生更加直观地感知“有限”与“无限”，有利于知识的内化.

这样借助图形的直观，凸显概念的本质，有利于概念的深化，有利于锻炼学生逻辑推理能力，促进学生数学核心素养的落实.

教学思考

1. 开展自主探究，鼓励逻辑论证

数学学习是一种传承，更是一种发展. 教学中教师不是直接将知识教给学生，而是提供机会让学生去发现、去探索、去创造，让学生用数学的眼光观察世界，培养学生的思维能力，提升学生的数学素养.

2. 巧借直观想象，提升推理能力

直观想象和逻辑推理是数学核心素养的重要组成部分，它们既相对独立，又相互融合. 直观想象为逻辑推理提供方向，而逻辑推理为直观想象提供依据，两者协调发展有利于学生更好地理解数学，树立善于思考、严谨求学的科学精神，提高自主学习、实践探究的能力.

在本课教学中，教师引导学生从正方形入手，让学生经历操作、猜想、交流、推理等过程，使得推理过程变得更加生动、有趣. 在这一过程中，学生深度思考与探索，提升了数学思维品质.

总之，数学教学不是简单地让学生接受知识，更重要的是让学生理解知识. 因此，教师要改变单一的讲授式教学，要创造机会让学生去发现、去探索、去归纳，从而让学生获得对知识真正的理解，有效激发学习热情，提高学习品质.

参考文献：

[1]刘洪超，周杨. 历史视角的“无理数”概念教学思考——基于对无理数概念教学浅表化现象的分析[J]. 中学数学杂志，2021（02）：27-30.