基于深度学习的微专题教学实践与思考

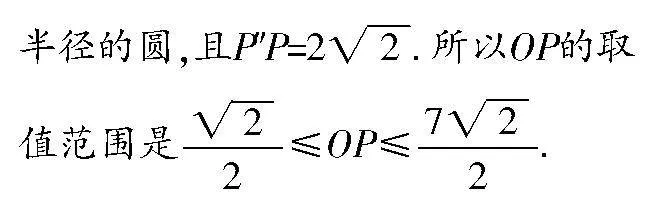
[摘 要] 基于深度学习的微专题教学是一种深入且高效的教学模式，对复习教学与优化学生的数学思维具有重要价值. 文章以“旋转构造相似三角形”的复习教学为例，分别从旋转全等形、旋转相似形与旋转圆形三类经典问题出发，强调从微专题的角度开发课堂，是形成个性化课例教学的基础，也是践行深度学习理念的基本途径.

[关键词] 微专题;深度学习;旋转

新课改背景下的数学课堂与传统课堂相比，多了很多新的教学手段与方法，课堂也注入了很多新的活力. 然而，仍有部分学生习惯性地被动学习，缺少将新旧知识相联系的习惯，导致对问题的思考不深入，对知识的理解浮光掠影. 若想改善这一现象，最好的办法就是践行深度学习理念，让学生真正掌握知识本质，对知识间的联系产生明确认识. 微专题教学属于一种高针对性、小切入点的专题教学模式，其对推进深度学习具有重要意义.

教学分析

在旋转变换的基础上探寻点的运动轨迹或线段的最值问题是初中阶段数学教学的重点与难点之一，在中考考题中也常有出现. 此类问题因涉及旋转变换，对学生空间思维要求较高，尤其是动态图形的旋转给学生带来不小的挑战. 细细揣摩这类问题，会发现此类题型并非无规律可循，它们之间存在一定的共性特点，即问题提供的图形不会太复杂，只要梳理清楚点、线、形的从属关系，发现问题背后的隐含条件，再借助旋转变换构造图形，便能解决.

教学过程

（一）旋转全等形

在复习课中，将经典题源作为题根，不仅能帮助学生夯实知识基础，还能以此为母题进行改编，发展学生思维的灵活性. 揭露几何图形中所隐含的“旋转全等形”这一几何模型，对解决几何综合性问题具有帮助.

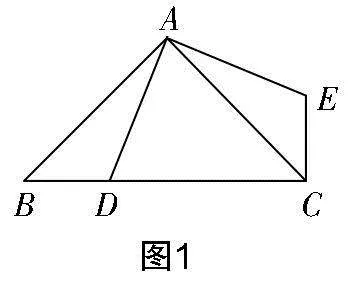
问题1 如图1所示，在Rt△ABC中，∠BAC=90°，BA=CA，D是BC边上不与点B，C重合的一个动点，连接AD，将AD绕点A逆时针旋转90°，设点D的对应点为E，连接EC，那么BD与EC之间有怎样的数量关系与位置关系？

于学生而言，本题难度不大. 在原有认知经验基础上，学生会自主证得△ADB≌△AEC，因此BD=EC，∠ACE=∠DBA=45°. 所以EC⊥BC. 因此BD与EC为垂直且相等的关系.

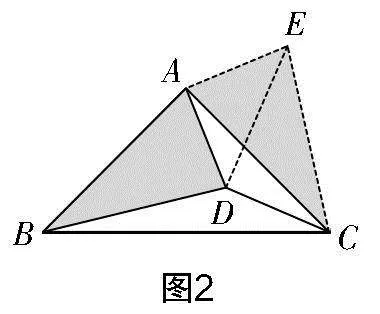
变式1 如图2所示，在Rt△ABC中，∠CAB=90°，BA=CA，点D在△ABC内，CD=1，BD=3，∠ADC=135°，线段AD的长是多少？

设计意图 解决本题的关键在于借助旋转构造全等三角形，通过转换将DE与题中明确给出的两条线段构成一个直角三角形，由此解得AD=2.

如果将△ABC内的点D迁移到三角形的外面，是否依然能快速获得AD的长呢？基于这一想法，教师可顺势提出变式2.

变式2 如图3所示，在四边形ABCD中，∠ACB=∠ABC=∠ADC=45°，CD=1，BD=3，则AD的长是多少？

设计意图 从形式上看，将点D由图形内转移到图形外，图形形状发生了较大改变，但从解题思路来看，它的解题方法与变式1高度相似，突出了解题过程“形变而理不变”的思想.

纵观此教学过程，变式的应用促使学生获得了举一反三的能力，并从变化的问题中发现了解题通法. 基于“绕定点旋转构造全等图形”这一动态变化，发现恒定不变的量，由此形成“以静制动”的解题技巧，提升理解与思辨能力.

（二）旋转相似形

基于学科角度来观察，数学中的“全等”与“相似”总是相伴相随，那么绕定点旋转构造图形时，是否可从“相似”的角度来分析呢？为了探索这一问题，笔者带领学生以特殊直角三角形的旋转为切入点展开分析.

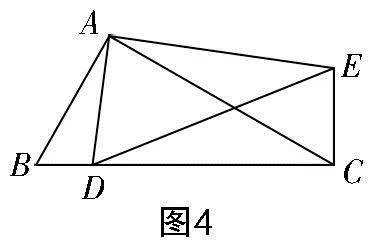
问题2 如图4所示，在△ABC与△ADE中，∠BAC=∠EAD=90°，点D在BC边上，且与点B和点C不重合，连接CE，∠ADE=∠ABC=60°，那么线段CE与BD之间有怎样的数量关系和位置关系？

拓展1 如图5所示，在Rt△ABC中，AB=3，AC=4，∠CAB=90°，D是BC边上的一个动点，连接AD，将点A作为直角顶点作Rt△DEA，令∠EDA=60°，连接CE，那么线段CE最短是多少？（解题过程略）

设计意图 题设条件明确给出两条已知线段与待求线段BD之间的关系为“共用一个端点D”，根据这一条件与变式2进行类比，构造直角三角形之后利用勾股定理实施求解. 逐层递进的问题让学生切身体会到了“绕定点旋转构造相似形”是解决这类问题的核心，此为发展学生建模能力的过程.

（三）旋转圆形

探索旋转类问题时，需将点的运动轨迹、直线运动、弧形运动问题进行辨析. 从某种意义上来说，弧形运动看似复杂，但解题思路并没有什么新奇的地方，解题本质不变. 为了帮助学生理解这一点，笔者让学生在不同图形的变化中进一步体会如何用静态的方法解决动态图形问题.

问题3 如图8所示，点O为AB的中点，AB=4，☉O的半径r=1，D为☉O上的一个动点，连接BD，同时把线段BD围绕点D逆时针旋转90°，将旋转后点B的对应点标注为点C，连接AC，那么线段AC的取值范围是什么？

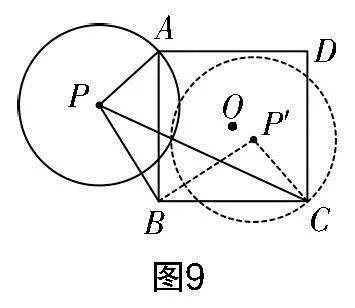
拓展1 如图9所示，若P为正方形ABCD外一点，正方形ABCD的中心为O，AP=3，BP=4，则DP的最小值、CP的最大值分别是多少？OP的取值范围呢？

半径的圆. 所以3+4为线段CP的最大值. 以此类推，不难探索到线段DP的最小值. 至于OP的取值范围，可从如下角度去思考：将△APB绕点B顺时针旋转45°，并缩小到原来的，得到△OP″B，得到动点O的运动轨迹为以点P″为圆心、为

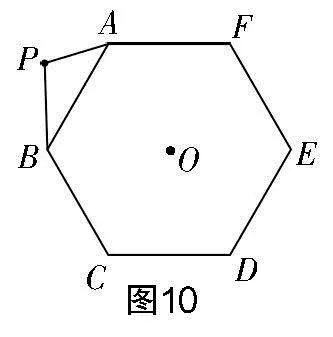
拓展2 如图10所示，已知正六边形ABCDEF的中心为O，其外有一点P，AP=3，BP=4，求CP的最大值，DP的最小值，以及OP的取值范围.

设计意图 虽然拓展2中问题的载体发生了改变，但没有改变其核心解题思路. 解决此类问题，基本遵循如下流程：分析图形中动点、定点所在的图形，探索待求线段之间所具备的位置关系，基于观察与分析思考围绕哪个定点旋转可以构造出相似图形，由此暴露新图形与特定条件间所具备的隐含关系，找到新动点所处的定圆. 如此设计可进一步帮助学生理顺解题思路，让学生体悟“动中探定”的一般流程，为形成解题通法奠定基础.

教学思考

（一）精选例题、揭露规律是微专题教学的基础

核心素养导向下的数学教学需在“双减”的基础上，精心设计教学方案，让学生在少而精的问题中发现解决问题的一般规律，获得知识或思想方法的融会贯通，形成举一反三的解题能力. 本节课，教师根据学情与教情，精心挑选了三类典型问题带领学生展开探索与分析，学生的思维随着问题的演变逐渐深入，不仅获得了解决这些问题的基本方法，还对一系列转化过程有了明确认识，获得了从“动”中发现“定”与从“定”中发现“变”的规律，真正落实了深度学习，体现了思维的创造性与灵活性.

（二）以生为本、深度探索是微专题教学的关键

《义务教育数学课程标准（2022年版）》明确指出，学生是学习的主体，是课堂的主人. 教师应时刻谨记这一点，才能落实“立德树人”的理念. 微专题应用在复习教学中，最大的特点是“既微又专”，主要体现在核心知识明确、探索过程清晰、思维含量高、探索程度深等方面. 本节课的探索主题为“旋转构造相似三角形”，那么一切教学活动的开展，均以这一知识点为核心. 整个探索过程，教师都将主动权交给学生，鼓励学生以独立思考、自主分析、合作交流等模式挖掘问题的本质，提炼思想方法，归纳解决问题的一般流程，取得了不错的教学成效.

（三）方法提炼、发展素养是微专题教学的目标

新课标引领下的初中数学教学，要将学生的发展作为教学的首要目标. 学生的发展主要体现在数学思想方法的提炼、思维品质的提升、关键能力的形成与人格的建立等方面. 复习教学是基于学生已有认知经验的巩固、提炼与升华，因此更需要关注对“人”的教育. 本节课，学生在对几个经典问题的探索中，不断感知数形结合、转化与化归、类比等思想方法对解题的重要性;变式与拓展的应用，进一步拓宽了学生的视野，让学生对“动”“定”转化问题有了更为深刻的认识;解题中，学生通过对问题的分析与总结，逐步提升了数学概括、逻辑推理、运算等素养，这些都是发展核心素养的必备条件.

总之，基于“小专题，大视野”的视角进行微专题复习教学，不仅能将深度学习、以生为本等理念落到实处，还能推进学生思维的发展，达到“立德树人”的目标. 因此基于深度学习的微专题复习教学是促进学生学力发展的重要举措.