有源缓冲型逆变器功率解耦技术研究

摘" 要：

为实现单级单相升压逆变并能有效抑制直流侧二次纹波电流，提出一种带有源缓冲的电流型逆变器电路拓扑，研究该逆变器的6种电路模态并提出其两模态调制策略和三模态调制策略，设计2种调制策略下的模型预测控制策略，提供主电路参数设计准则。从储能电感电流的最大脉动量与二次纹波含量两方面对2种调制策略进行对比分析，得出了三模态调制策略具有更好纹波抑制效果的结论。对2种调制策略下的逆变器进行仿真分析，仿真结果表明，三模态调制下电路的输出电压总谐波失真率、电感电流相对脉动量与二倍频含量均低于两模态调制下的数据。设计并搭建500VA 48VDC/220V50HzAC有源缓冲型单级单相升压逆变器实验装置，给出了三模态调制下基于模型预测控制的逆变器实验波形，进一步证实了所提研究方案在实现单级升压逆变的同时具有二次纹波抑制能力。

关键词：单相逆变器；单级升压；调制策略；有源缓冲；功率解耦；模型预测控制

DOI：10.15938/j.emc.2024.06.010

中图分类号：TM464

文献标志码：A

文章编号：1007-449X（2024）06-0098-11

收稿日期： 2023-06-29

基金项目：福建省自然科学基金（2018J01757）

作者简介：陈亦文（1977—），女，博士，副教授，研究方向为新能源发电技术、电力电子技术在电力系统中的应用等；

童筱涵（1998—），女，硕士研究生，研究方向为新能源发电技术；

吕" 涛（1995—），男，硕士，助理工程师，研究方向为新能源发电技术；

李文博（1999—），男，硕士研究生，研究方向为新能源发电技术；

江加辉（1989—），男，博士，副教授，研究方向为电力电子变流技术、新能源发电技术。

通信作者：江加辉

Research on active buffered inverter power decoupling technology

CHEN Yiwen1，" TONG Xiaohan1，" L Tao2，" LI Wenbo1，" JIANG Jiahui3

（1.Fujian Key Laboratory of New Energy Generation and Power Conversion， Fuzhou University， Fuzhou 350116， China; 2.China Changjiang Power Company Limited， Yichang 443002， China; 3.School of Electrical Engineering， Qingdao University， Qingdao 266071， China）

Abstract：

In order to realize a single-stage single-phase boost inverter and effectively suppress the secondary ripple current on the DC side， a current inverter circuit topology with source buffer was proposed. Six circuit modes of the inverter were investigated and two-modal modulation strategies and three-modal modulation strategies were proposed. A model prediction control strategy under the two modulation strategies was designed， and design guidelines for the parameters of the main circuit were provided. The two modulation strategies were compared and analyzed in terms of the maximum pulsation of the storage inductor current and the secondary ripple content. It is concluded that the three-modal modulation strategy has a better ripple suppression effect. The inverter under the two modulation strategies was simulated and analyzed， and the simulation results show that the total harmonic distortion rate of the output voltage， the relative pulsation and dual frequency content of the inductor current under three-mode modulation are lower than those under two-mode modulation. A 500VA 48VDC/220V50HzAC active buffered single-stage single-phase boost inverter experimental setup was designed and constructed， and the experimental waveforms of the inverter based on the model predictive control under the three-mode modulation were given， which further confirms that the proposed research scheme has the ability of secondary ripple suppression while realizing the single-stage boost inverter.

Keywords：single phase inverter; single-stage booster; modulation strategy; active buffer; power decoupling; model predictive control

0" 引" 言

随着全球经济的发展，能源危机和环境恶化问题日益严重，以燃料电池、光伏为代表的新能源发电系统越来越得到人们的重视［1-5］。由于光伏电池和燃料电池的输出电压往往为较低直流电，且波动范围较大，难以直接利用，需要升压型逆变器将直流电能转换成交流电能并传输到电网上或供负载使用。传统电压型逆变器需构建升压回路，这不仅会增加生产成本，降低变换器的效率，而且随着功率变换的等级增多，系统的可靠性也会下降［6］。电流型逆变器可以实现升压逆变，但是传统单级单相电流型逆变器在降压阶段储能电感无法去磁，电感能量无法达到平衡，电感电流将持续升高，导致输出波形畸变［7］。此外，单相逆变器输入电流含有低频纹波，这些低频纹波将会影响逆变器的性能，造成一些不良危害和影响［8-10］。因此，为了适应新能源发电等低输入电压的应用场合，设计一款具有功率解耦功能的单相升压逆变器具有重要意义。

为了更好地抑制单相逆变器输入侧电流二次纹波，研究人员提出了许多的解决方案，通常可分成优化电路拓扑以及改进控制策略两类。文献［11］在传统两级式逆变器的交流侧并联一个有源LC解耦电路，将低频脉动功率转移到该解耦电路，仿真和实验中输入电流二次谐波含量分别为1.73%和8%，虽实现了输入侧电流二次纹波的抑制，但引入较多的功率开关且解耦电路略显复杂。文献［12］提出了一种含有源解耦电路的单相Buck-Boost逆变器，通过在前端Buck-Boost变换器和电压源桥式逆变器上增加一个小的薄膜电容Cd吸收低频脉动功率达到抑制输入侧低频纹波电流的目的，但受到电路工作原理的限制，其占空比调节范围较窄。文献［13］提出了在电压环中插入陷波器并引入负载电流前馈的控制策略，进一步提升了二倍频电流抑制能力和系统的响应速度，仿真与实验中输入电流二次纹波含量分别为1.5%和4.05%，该方案二次纹波抑制效果较好，但中间直流母线电容承担几乎全部的二倍频电流，容值较大。文献［14］在文献［13］基础上做出了改进，通过引入电容支路串联虚拟阻抗来抵消电容电压二次脉动的作用，大大减小了电容容值，提升了前级DC/DC的二倍频电流抑制能力和动态特性，仿真与实验中输入电流二次纹波含量分别为2.18%和5.57%，纹波抑制效果较好。文献［15-16］使用波形控制的方法通过在每个电容器的参考电压上增加叠加直流电压和二阶电压分量来减轻脉动功率，但也引入了4次谐波分量，文献［16］实验中输入电流二次纹波含量约为9.39%，纹波抑制效果还有待提高。文献［17］在电流纹波阻尼控制的基础上提出了一种基于三电平升压馈电单相电压源逆变器（voltage source inverter，VSI）的电容电压纹波互补控制算法，通过对两个电容器上的电荷进行重新分配，使其电压纹波相互补充，进一步减小了直流链路电容，实现输入侧电流二次纹波抑制，但该方案控制更为复杂。

为简化解耦电路与控制策略，并进一步提高电路的输入侧二次纹波抑制能力，本文提出一种新颖的有源缓冲型单级单相逆变器电路拓扑及两模态与三模态2种调制策略，设计2种调制策略下的模型预测控制（model predictive control，MPC）策略，并从储能电感电流的最大脉动量与二次纹波含量两方面对2种调制策略进行对比分析，设计其关键电路参数，并通过仿真和实验验证所提方案的可行性。

1" 电路拓扑及其调制策略

1.1" 电路拓扑

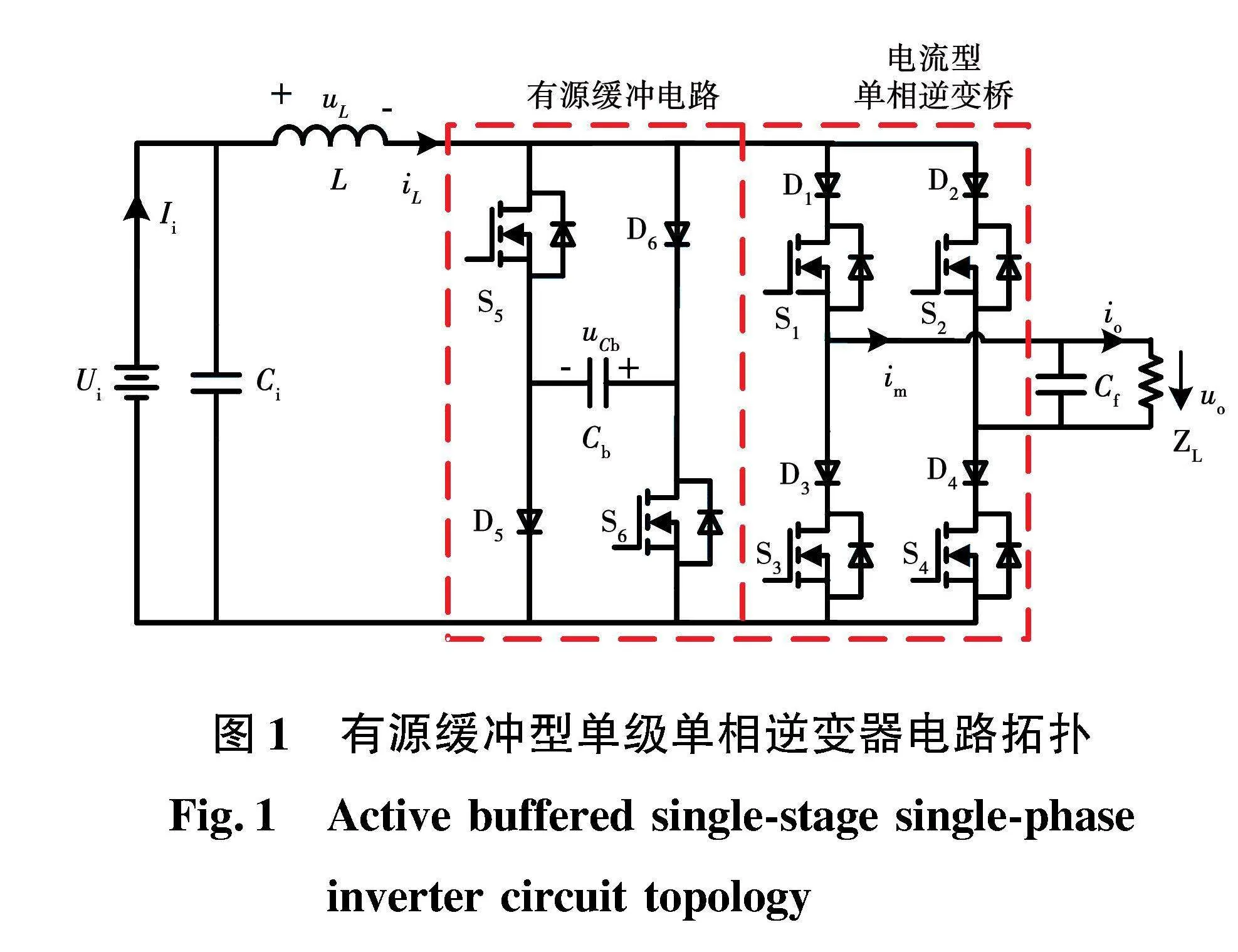
所提出的有源缓冲型单级单相逆变器电路结构如图1所示。该电路由输入源Ui、输入滤波电容Ci、储能电感L、有源缓冲电路、电流型单相逆变桥S1（D1）～S4（D4）和输出滤波电容Cf级联构成。有源缓冲电路通过放电开关S5、S6控制缓冲电容Cb的充放电状态，将负载侧低频脉动功率转移到缓冲电容Cb，实现功率解耦。

1.2" 电路模态

所提逆变器在一个工频周期内共有6个电路模态，分别为：

1）左桥臂直通充磁模态：S5、D5导通，Ui通过Ui→L→S5→D5回路给L充磁，同时输出滤波器Cf给负载ZL供电。

2）右桥臂直通充磁模态：S6、D6导通，Ui通过Ui→L→D6→S6回路给L充磁，同时输出滤波器Cf给负载ZL供电。

3）正半周馈能模态：S1、S4导通，Ui分别给Cf和ZL供电，正向调制电流im路径为Ui→L→D1→S1→ZL、Cf→D4→S4。

4）负半周馈能模态：S2、S3导通，Ui分别给Cf和ZL供电，负向调制电流im路径为Ui→L→D2→S2→ZL、Cf→D3→S3。

5）缓冲电容充电模态：S5、S6截止，D5、D6自然导通，L通过L→D6→Cb→D5回路给Cb充电，同时Cf给ZL供电。

6）缓冲电容放电模态：S5、S6导通，Cb通过Cb→S6→Ui→L→S5回路给L充磁，同时Cf给ZL供电。

为保证馈能模态时D5和D6处于截止状态，电容电压须满足

uCb（t）gt;|uo（t）|。（1）

考虑留取一定余量，有

uCbmingt;|uomax|。（2）

1.3" 调制方式

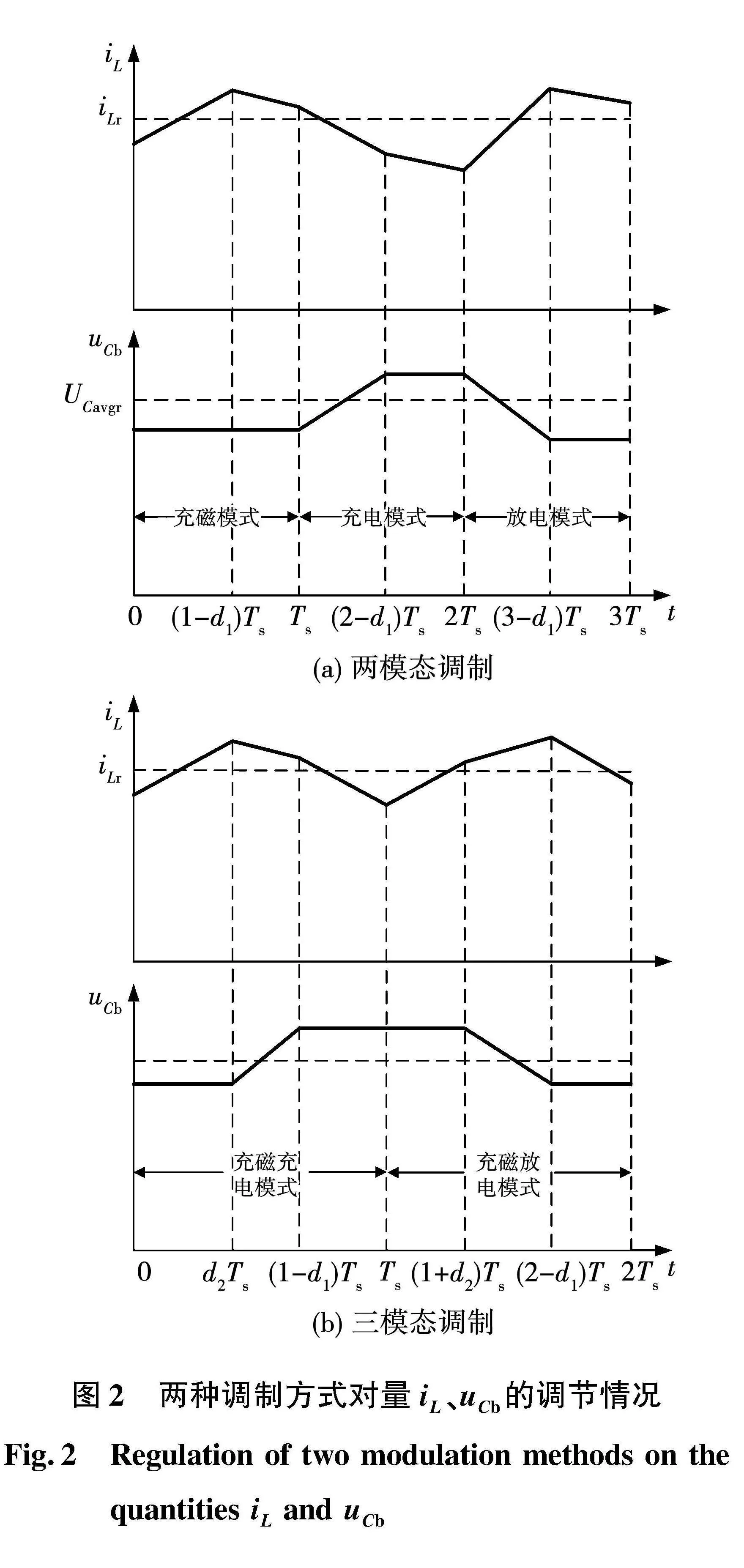
根据每个开关周期Ts的电路模态数量不同，所提出逆变器存在2种调制方式，分别为两模态调制方式和三模态调制方式。这2种调制方式对储能电感电流iL、缓冲电容电压uCb的调节情况如图2所示。

两模态调制方式每个开关周期Ts有2个电路模态，根据电路模态的不同组合，分成3种工作模式如图2（a）所示，分别为：

1）充磁模式：由d1Ts期间馈能模态和（1-d1）Ts期间充磁模态构成，该模式下uCb不变，iL根据馈能占空比的大小存在上升或下降2种情况，这里以iL上升为例。

2）充电模式：由d1Ts期间馈能模态和（1-d1）Ts期间缓冲电容充电模态构成，该模式下uCb上升、iL下降。

3）放电模式：由d1Ts期间馈能模态和（1-d1）Ts期间缓冲电容放电模态构成，该模式下uCb下降、iL上升。

三模态调制方式每个开关周期Ts有3个电路模态，根据电路模态的不同组合，分为2种工作模式，如图2（b）所示。其中充磁充电模式由d2Ts期间充磁模态、（1-d1-d2）Ts期间缓冲电容充电模态和d1Ts期间馈能模态构成；充磁放电模式由d2Ts期间充磁模态、（1-d1-d2）Ts期间缓冲电容放电模态和d1Ts期间馈能模态构成。2种工作模式的区别在于（1-d1-d2）Ts期间模态不同，放电模态中uCb下降、iL上升，充电模态中uCb上升、iL下降。

2" 控制策略

2.1" 基于MPC的逆变系统功率解耦策略

所提出的逆变器系统控制逻辑如图3所示。输出电压环通过PI调制获得馈能占空比d1。缓冲电容电压环通过PI调制获得储能电感电流iL的参考信号iLr。MPC控制器以iL在一个开关周期结束时的值与iLr的误差最小为目标，在两模态调制中仅计算出工作模式判断信号me和正负半周判断信号a；在三模态调制中计算出me、a和充磁占空比d2。其中me和d2由代价函数决定，正负半周判断信号a=sgn（uo_pi）。

2.2" MPC控制器代价函数

由于两模态调制和三模态调制每个开关周期Ts的电路模态数量不同，因此储能电感电流iL在一个开关周期结束时的值与iLr的误差表达式不同，即模型预测控制器的代价函数不同。

1）两模态调制下的代价函数。

两模态调制时的代价函数为

ΔiL=min（Δim，Δic，Δid）。（3）

式中：

Δim=iL+UiL（1－d1）Ts+

Ui-sgn（uo_piuo）|uo|Ld1Ts-iLr，me=00；

Δic=iL+Ui-uCbL（1－d1）Ts+

Ui-sgn（uo_piuo）|uo|Ld1Ts-iLr，me=01；

Δid=iL+Ui+uCbL（1－d1）Ts+

Ui-sgn（uo_piuo）|uo|Ld1Ts-iLr，me=10。（4）

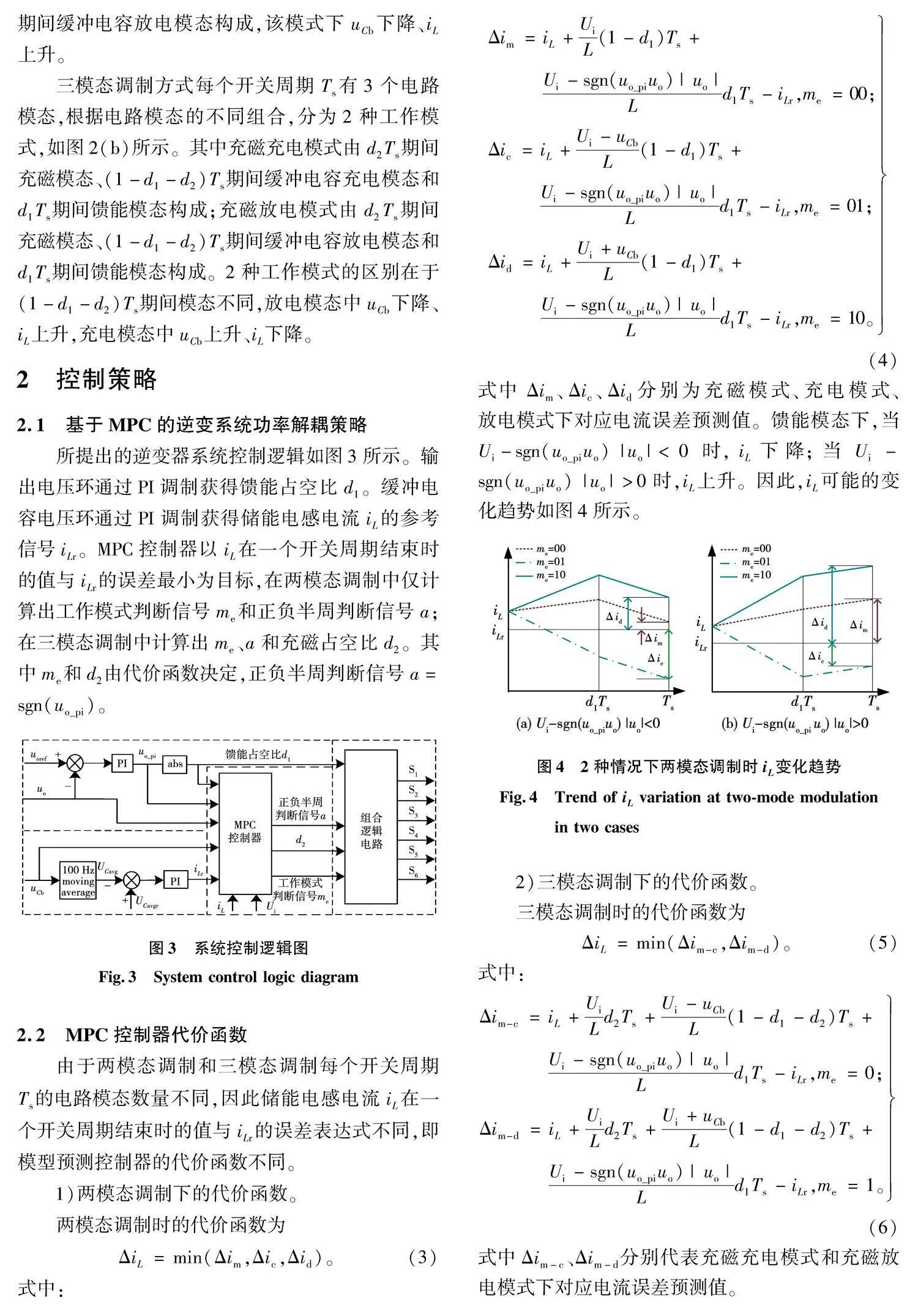
式中Δim、Δic、Δid分别为充磁模式、充电模式、放电模式下对应电流误差预测值。馈能模态下，当Ui-sgn（uo_piuo） |uo|lt;0时，iL下降；当Ui-sgn（uo_piuo） |uo|gt;0时，iL上升。因此，iL可能的变化趋势如图4所示。

2）三模态调制下的代价函数。

三模态调制时的代价函数为

ΔiL=min（Δim-c，Δim-d）。（5）

式中：

Δim-c=iL+UiLd2Ts+Ui-uCbL（1-d1-d2）Ts+

Ui-sgn（uo_piuo）|uo|Ld1Ts-iLr，me=0；

Δim-d=iL+UiLd2Ts+Ui+uCbL（1-d1-d2）Ts+

Ui-sgn（uo_piuo）|uo|Ld1Ts-iLr，me=1。（6）

式中Δim-c、Δim-d分别代表充磁充电模式和充磁放电模式下对应电流误差预测值。

由图3可知，通过输出电压环可直接求得馈能占空比d1，代入式（6）可得电流误差预测值关于d2的一次函数，其中d2取值范围为［0，1-d1］。

为预测电路工作模式，令1-d1-d2=0，则Δim-c=Δim-d=Δim，若Δimgt;0，一个开关周期Ts结束iL＞iLr，故需令（1-d1-d2）Tsgt;0且对应充电模态，即逆变器下一个开关周期将工作在充磁充电模式，me=0；若Δim＜0，一个开关周期Ts结束iL＜iLr，故需令（1-d1-d2）Tsgt;0且对应放电模态，即逆变器下一个开关周期将工作在充磁放电模式，me=1。

因此通过调节充磁占空比d2，便能使每个开关周期结束时储能电感电流iL回到参考值iLr，进一步令ΔiL=0可得：

d2=uCb-UiuCb（1-d1）+

sgn（uo_piuo）|uo|-UiuCbd1+

iLr-iLuCbTsL，me=0；

d2=uCb+UiuCb（1-d1）+

Ui-sgn（uo_piuo）|uo|uCbd1+

iL-iLruCbTsL，me=1。（7）

根据上述分析，三模态MPC控制器代价函数可预测出工作模式判断信号me及充磁占空比d2。

3" 原理特性

3.1" 2种调制下储能电感电流变化规律

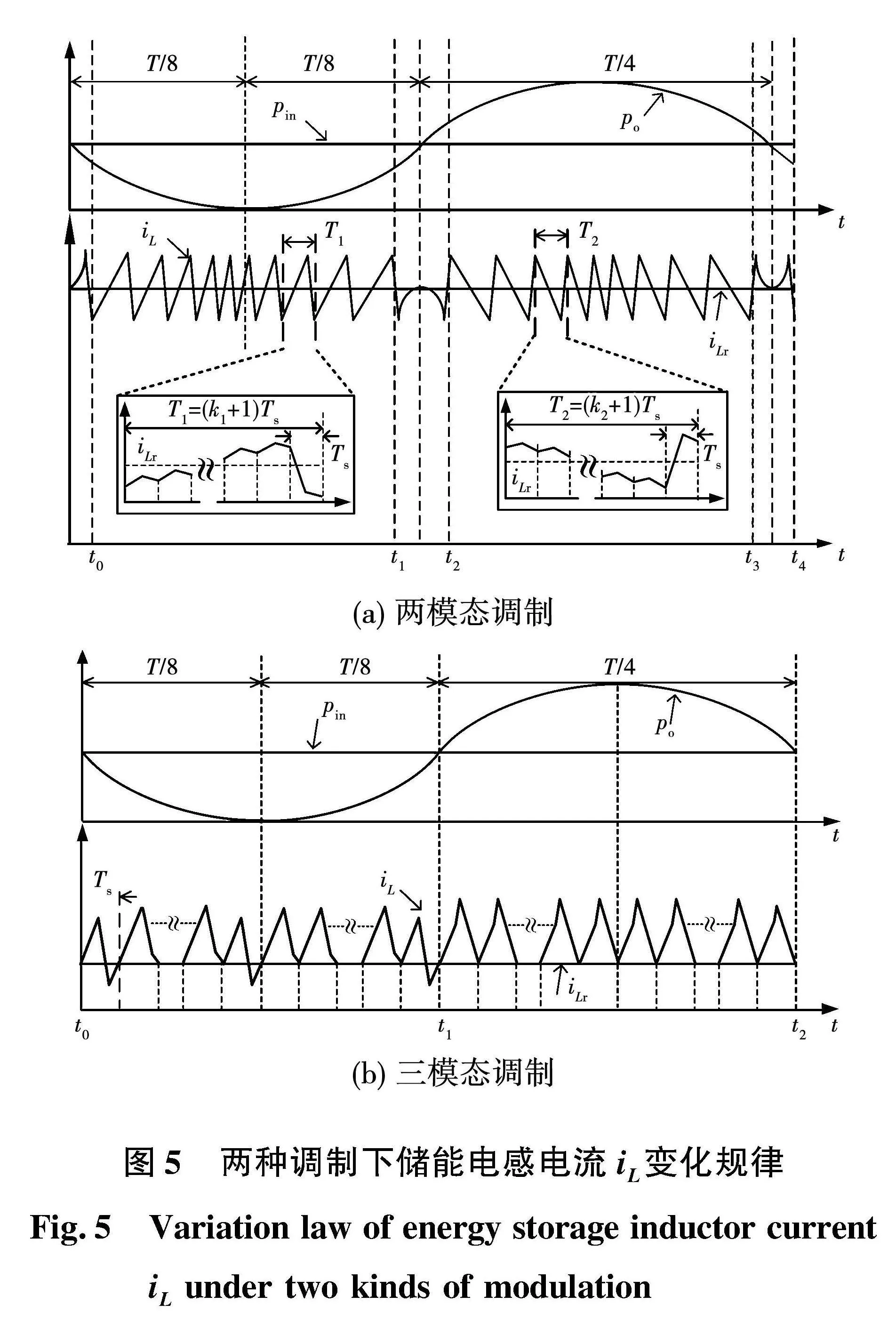
2种调制方式下，逆变系统储能电感电流iL变化规律如图5所示。

1）两模态调制。

由图5（a）可知，两模态调制时逆变器在一个输出功率周期（半个工频周期T/2）内的工作模式分布可划分为4个区间。根据4个区间内不同工作模式的分配可分为Mc1、Mc2和Ma 3种工况。其中：Mc1由k1个Ts充磁模式加1个Ts充电模式构成，Mc2由k2个Ts充磁模式加1个Ts放电模式构成，Ma仅存在充磁模式。

［t0-t1］：此区间逆变器工作在Mc1。由于polt;pin，该区间充磁模式下每个开关周期结束时iL都会上升，充电模式下电容吸收电感过剩能量，iL下降。由于缓冲电容电压相对较高，逆变器在充电模式下iL变化速率快于充磁模式，为使iL跟踪iLr，需k1个充磁模式补偿电流的下降。该区间po与pin差值先增大后减小，iL上升速率先增大后减小，因此k1先减小后增大，iL脉动先由疏变密，后由密变疏。

［t1-t2］：po在pin附近，此区间由于输入输出能量差值较小，由代价函数可知，逆变器将工作在多个充磁模式构成的组合Ma，iL先减小后增大，其变化曲线呈弧形。

［t2-t3］：此区间逆变器工作在Mc2。由于pogt;pin，该区间充磁模式下每个开关周期结束时iL都会下降。放电模式下电容释放能量维持电感电流，iL上升。由于缓冲电容电压相对较高，逆变器在放电模式下iL变化速率快于充磁模式，为使iL跟踪iLr，需k2个充磁模式补偿电流的上升。该区间po与pin差值先增大后减小，iL下降速率先增大后减小，因此k2先减小后增大，iL脉动先由疏变密，后由密变疏。

［t3-t4］：同［t1-t2］ 类似，工作在Ma。这里不再赘述。

两模态调制下［t0-t4］每半个工频周期都按照Mc1、Ma、Mc2、Ma规律变化，因此带来少量以二倍频为主的低频纹波分量。

2）三模态调制。

由图5（b）可知，三模态调制时逆变器在一个输出功率周期内的工作模式分布可划分为2个区间。

［t0-t1］：此区间polt;pin，由MPC控制原理，逆变器将工作在充磁充电模式，当Ui-sgn（uo_piuo）×|uo|lt;0时，每个高频开关周期的（0，Ts）期间iL＞iLr，Ts时刻iL=iLr；当Ui-sgn（uo_piuo） |uo|gt;0时，每个高频开关周期的（0，Ts）期间iL围绕iLr上下波动，Ts时刻iL=iLr。

［t1-t2］：此区间pogt;pin，由MPC控制原理，逆变器将工作在充磁放电模式，且该区间必然满足Ui-sgn（uo_piuo） |uo|lt;0，因此该区间每个高频开关周期的（0，Ts）期间iL＞iLr，Ts时刻iL=iLr。

可见三模态调制下每个开关周期结束时储能电感电流iL都能回到参考值iLr。

3.2" 2种调制方式下电感电流最大脉动量分析及对比

1）电感电流最大脉动量。

由3.1节分析可知，两模态调制下系统工作在Ma工况时iL脉动量小于前2种工况，所以计算iL最大脉动量时不考虑该工况。因此iL的变化可能存在A到D 4种情况如表1所示，其中A、B对应Mc1，C、D对应Mc2。

由MPC控制原理可知，D不存在，iL脉动量在充电模式下为iL下降量，放电模式下为iL上升量。

因此两模态调制下iL的脉动量为：

Δi1（A）=uCb-UiL（1-d1）Ts；

Δi1（B）=2|uo|-UiLd1Ts+uCb-UiL（1-d1）Ts=

uCb-UiLTs+2|uo|-uCb-UiLd1Ts；

Δi1（C）=uCb+UiL（1-d1）Ts。（8）

为获得iL最大脉动量，对A、B、C 3种情况分别展开计算。以阻性负载情况为例，Δi1（A）与Δi1（C）达到最大值时，对应馈能占空比d1为最小值；Δi1（B）达到最大值时，对应馈能占空比d1为最大值。

结合控制策略可知：

d1max=ioiL≈2Po/UoiL=2UiUo；

d1min=0。（9）

将式（9）代入式（8）可得：

Δi1（A）max=UCavgr-UiLTs；

Δi1（B）max=（UCavgr-Ui）TsL+

2（2|uomax|-UCavgr-Ui）UiTsLUo；Δi1（C）max=UCavgr+UiLTs。（10）

式中UCavgr为缓冲电容电压平均限定值，由于UCavgr远大于纹波分量，故认为uCb近似等于UCavgr。

由式（10）可得两模态调制下iL的最大脉动量为

Δi1max=UCavgr+UiLTs。（11）

由3.1节分析可知，三模态调制下iL变化趋势存在3种情况，因此iL的脉动量为：

Δi2（a）=UiLd2Ts+Ui-|uo|Ld1Ts；

Δi2（b）=UiLd2Ts；

Δi2（c）=|uo|-UiLd1Ts。（12）

式中：Δi2（a）为充磁放电模式下iL的脉动量；Δi2（b）为充磁充电模式下Ui-sgn（uo_piuo） |uo|lt;0时iL的脉动量；Δi2（c）为充磁充电模式下Ui-sgn（uo_piuo）|uo|＞0时iL的脉动量。

以阻性负载情况为例，Δi2（c）达到最大值时，对应馈能占空比d1为最大值；Δi2（a）与Δi2（b） 达到最大值时，对应d2为最大值，d1为0。

结合控制策略可知：

d1max=ioiL≈2Po/UoiL=2UiUo；

d2max=UCavgr-UiUCavgr。（13）

将式（13）代入式（12）可得：

Δi2（a）max=Δi2（b）max=（UCavgr-Ui）UiTsLUCavgr；

Δi2（c）max=2（|uomax|-Ui）UiTsLUo。（14）

由式（14）可得三模态调制下iL的最大脉动量为

Δi2max=2（|uomax|-Ui）UiTsLUo。（15）

由于该逆变器应用于升压逆变场合，|Uo|gt;Ui，结合式（2），代入式（11）、式（15）得：

Δi1maxgt;TsL（2|Uo|+Ui）gt;TsL2Ui；

Δi2max=TsL2|Uo|－2UiUoUilt;TsL2Ui。（16）

由式（16）可知，两模态调制下iL的最大脉动量更高。

2）电感电流二次纹波含量。

由电感电流变化规律可知，两模态调制策略下iL存在二次疏密变化规律，故其中必然含有小部分以二倍频为主的低频纹波分量；而三模态调制下，由于每个开关周期结束iL都能回到iLr，iL无累积量，故单个开关周期内脉动量差别不大，同时不存在二次疏密变化规律，因此原理上iL二次纹波分量极低。可见相比于两模态调制策略，三模态调制策略具有相对更好的纹波抑制效果。

4" 主电路参数设计

2种调制策略下主电路参数设计思路一致，这里以三模态调制情况为例。

4.1" 储能电感

由式（15）可得三模态调制下储能电感电流最大纹波为

ΔiLmaxiLr=2（|uomax|-Ui）UiTsLUoPo/Ui=

2（|uomax|-Ui）U2iTsLUoPo。（17）

设储能电感电流纹波不大于kiL%，则

L≥2（|uomax|-Ui）U2iTsUoPokiL%。（18）

4.2" 缓冲电容

单相逆变器的输出电压、电流可表示为：

uo（t）=2Uosin（ωt）；

io（t）=2Iosin（ωt－φ）。（19）

忽略逆变器的功率损耗，由功率守恒可得输入功率

pin（t）=po（t）=UoIocosφ－UoIocos（2ωt－φ）。（20）

有源缓冲电路将功率中的二倍频分量转移到了缓冲电容上，即

pCb（t）=－uCb（t）iCb（t）=－uCb（t）CbduCb（t）dt=

UoIocos（2ωt－φ）。（21）

由式（21）可得缓冲电容电压为

uCb（t）=U2Cavgr+UoIoωCbsin（2ωt-φ）。（22）

由式（2）可得

uCbmin=U2Cavgr-UoIoωCbgt;|uomax|。（23）

则

Cbgt;UoIoω（U2Cavgr-u2omax）=Poω（U2Cavgr-u2omax）。（24）

5" 仿真分析

所提出的逆变器参数如表2所示，采用基于MPC的逆变系统功率解耦控制策略，在阻性（RL=96.8 Ω，PF=1）、阻感（RL=72.6 Ω、LL=203.8 mH、PF=0.75）以及阻容（RL=72.6 Ω、CL=49.7 μF、PF=0.75）负载下分别采用两模态调制方式和三模态调制方式进行仿真。其缓冲电容电压限定值UCavgr=400 V。

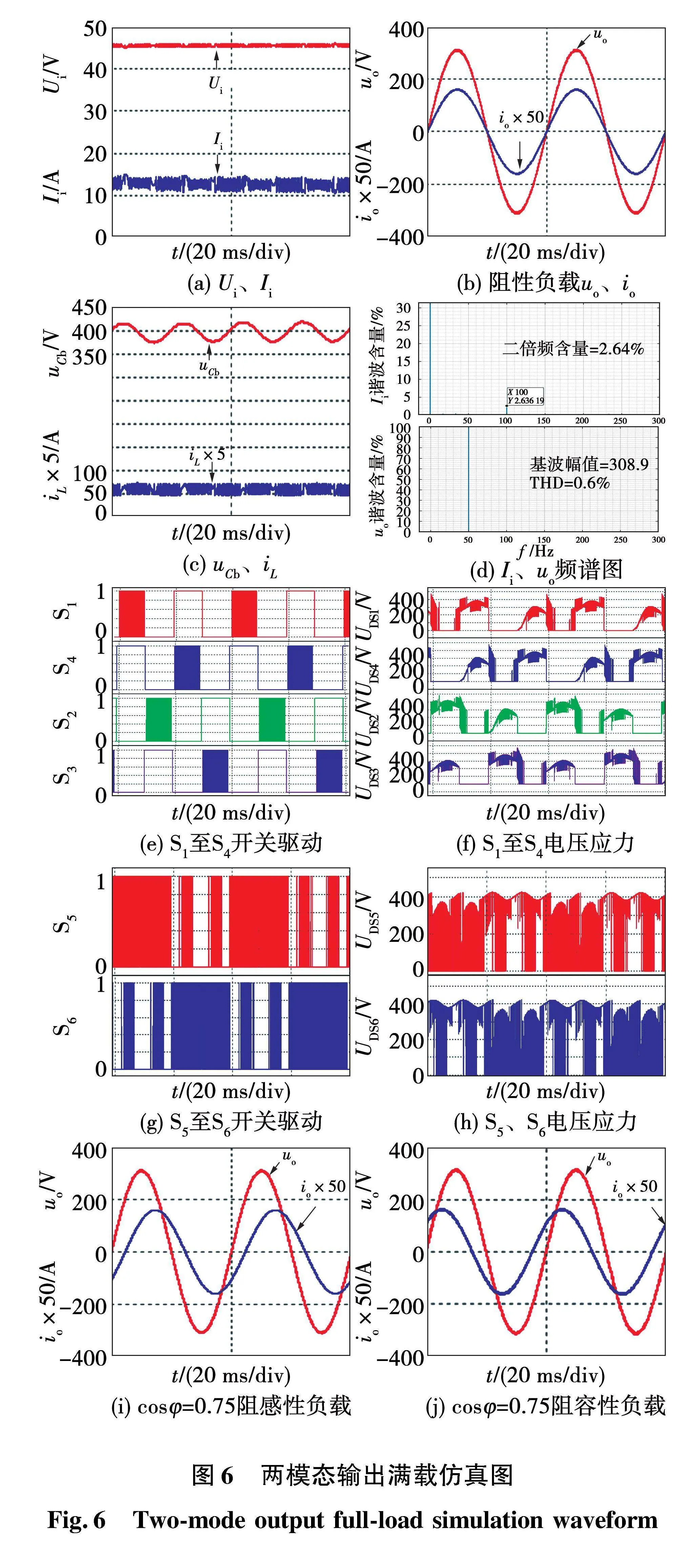
5.1" 两模态调制仿真分析

所提逆变器在两模态调制方式下稳态满载仿真波形图如图6所示，由图6可得：1）输出电压总谐波失真率（total harmonic distortion，THD）约为0.6%，波形质量较高；2）储能电感电流iL在限定值iLr附近脉动，相对脉动量为22.46%，二倍频含量约2.64%，低频分量较少，该系统具有较好纹波抑制能力；3）能驱动阻性、阻感性和阻容性负载，负载适应能力较强。

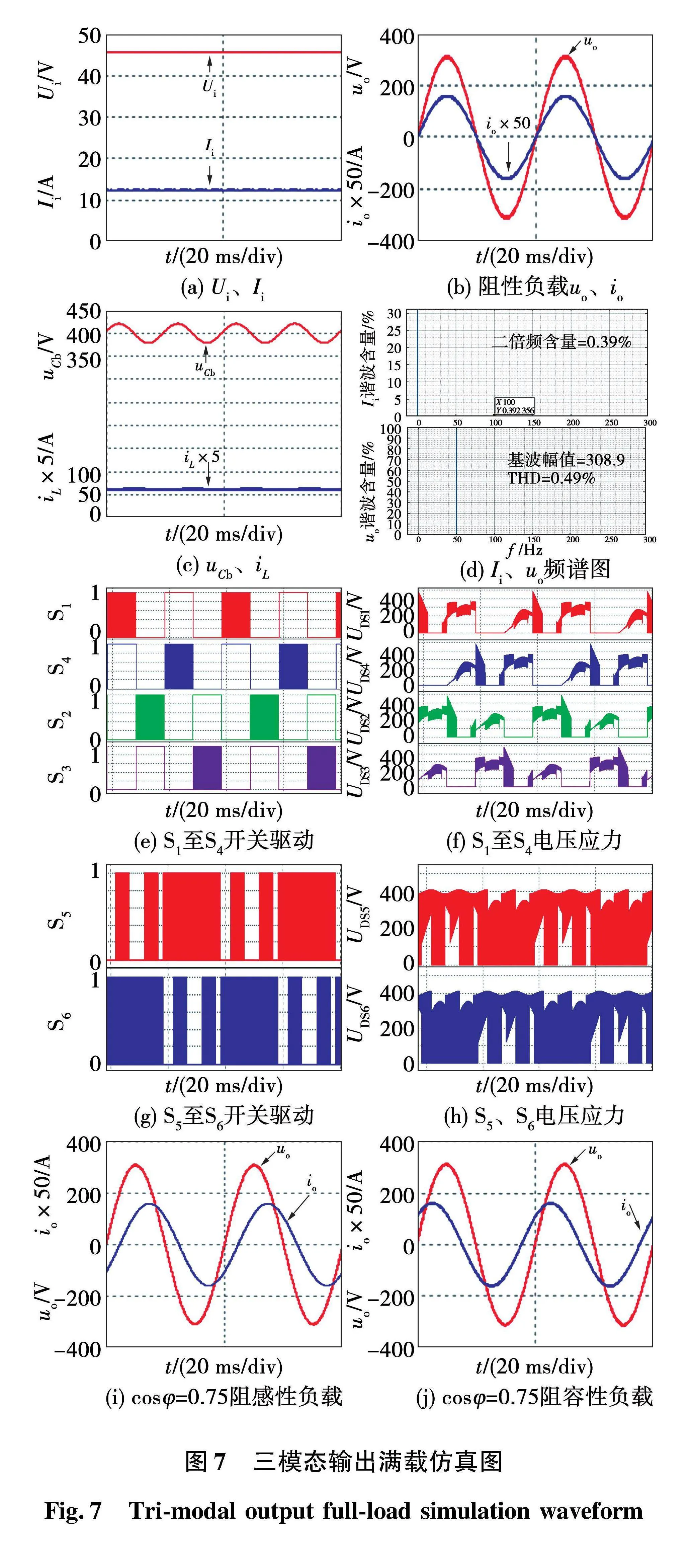
5.2" 三模态调制仿真分析

所提逆变器在三模态调制方式下稳态满载仿真波形图如图7所示，由图可得：1）输出电压THD约为0.49%，波形质量较高；2）储能电感电流iL在限定值iLr附近脉动，相对脉动量为4.15%，二倍频含量约0.39%，低频分量较少，该系统具有很好纹波抑制能力；3）能驱动阻性、阻感性和阻容性负载，负载适应能力较强。

5.3" 2种调制下仿真结果对比

分别对比图6和图7波形，1）由图6（a）、图7（a）可得：2种调制方式均能抑制输入电流的二次纹波分量，实现功率解耦，但三模态调制下输入电流脉动更小，近似为直流电流。2）由图6（b）、图7（b）可得：2种调制方式下均能实现单级单相升压逆变，输出稳定的220 V/50 Hz的交流电压。3）由图6（c）、图7（c）可得：2种调制方式下uCb都在400 V附近呈二倍频脉动，达到了将负载侧低频脉动功率转移到缓冲电容上的目的，但三模态调制方式下iL脉动更小。4）由图6（d）、图7（d）可得：满载时，三模态调制方式下输出波形质量与输入电流纹波抑制效果均优于两模态调制方式。

综合考虑逆变器的输出波形THD、输入电流二次纹波含量及电感电流脉动量，后续实验部分选择三模态调制作为调制方式。

6" 实验验证

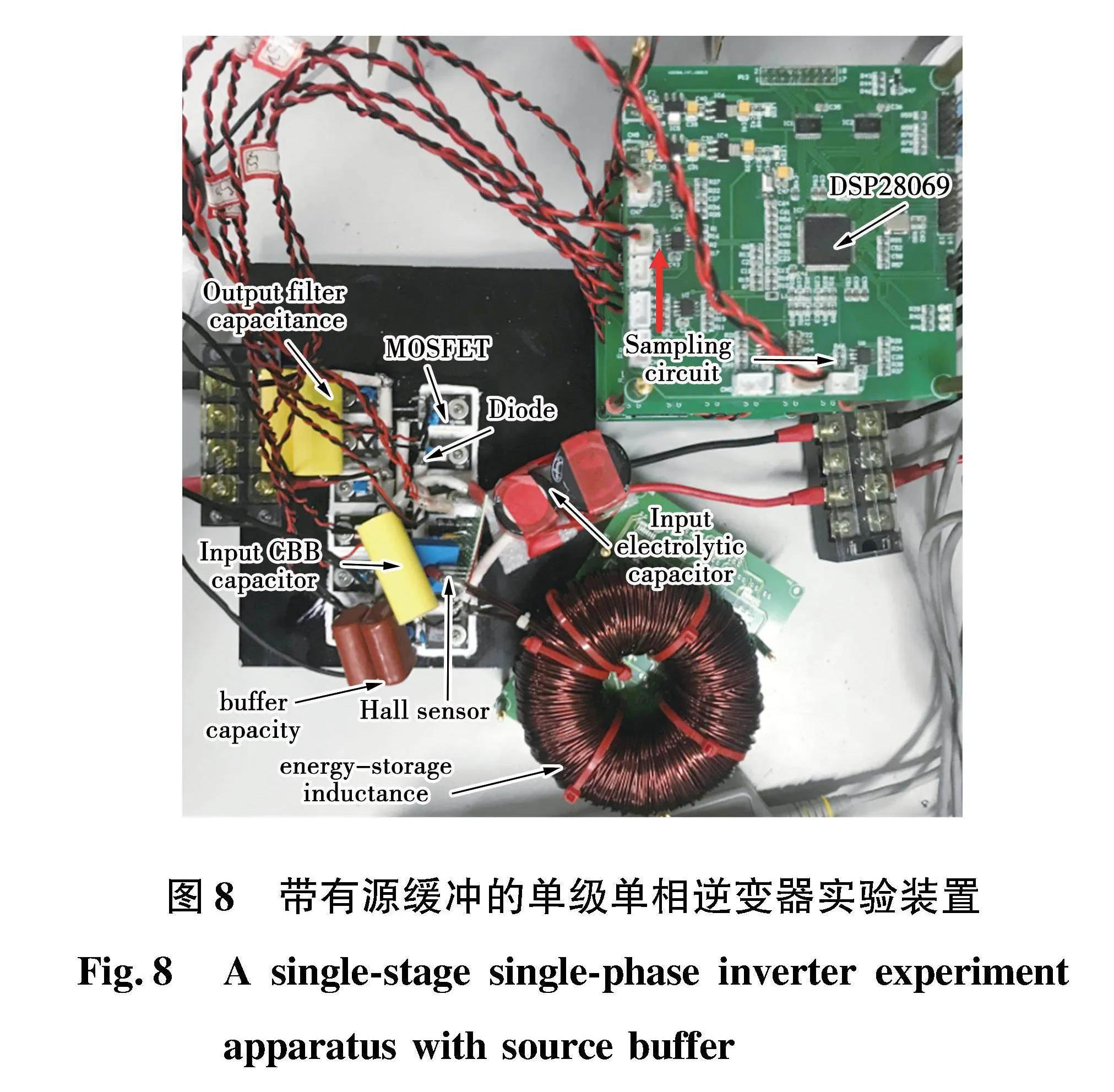
采用表2参数设计并搭建了一台500VA 48VDC/220V50HzAC有源缓冲型单级单相升压逆变器实验装置，如图8所示。在三模态调制方式下通过实验对电路的可行性及控制策略的可行性进行验证。其主电路功率开关S1～S6为IXFN66N85X ，二极管D1～D6为DSEI60-06A。

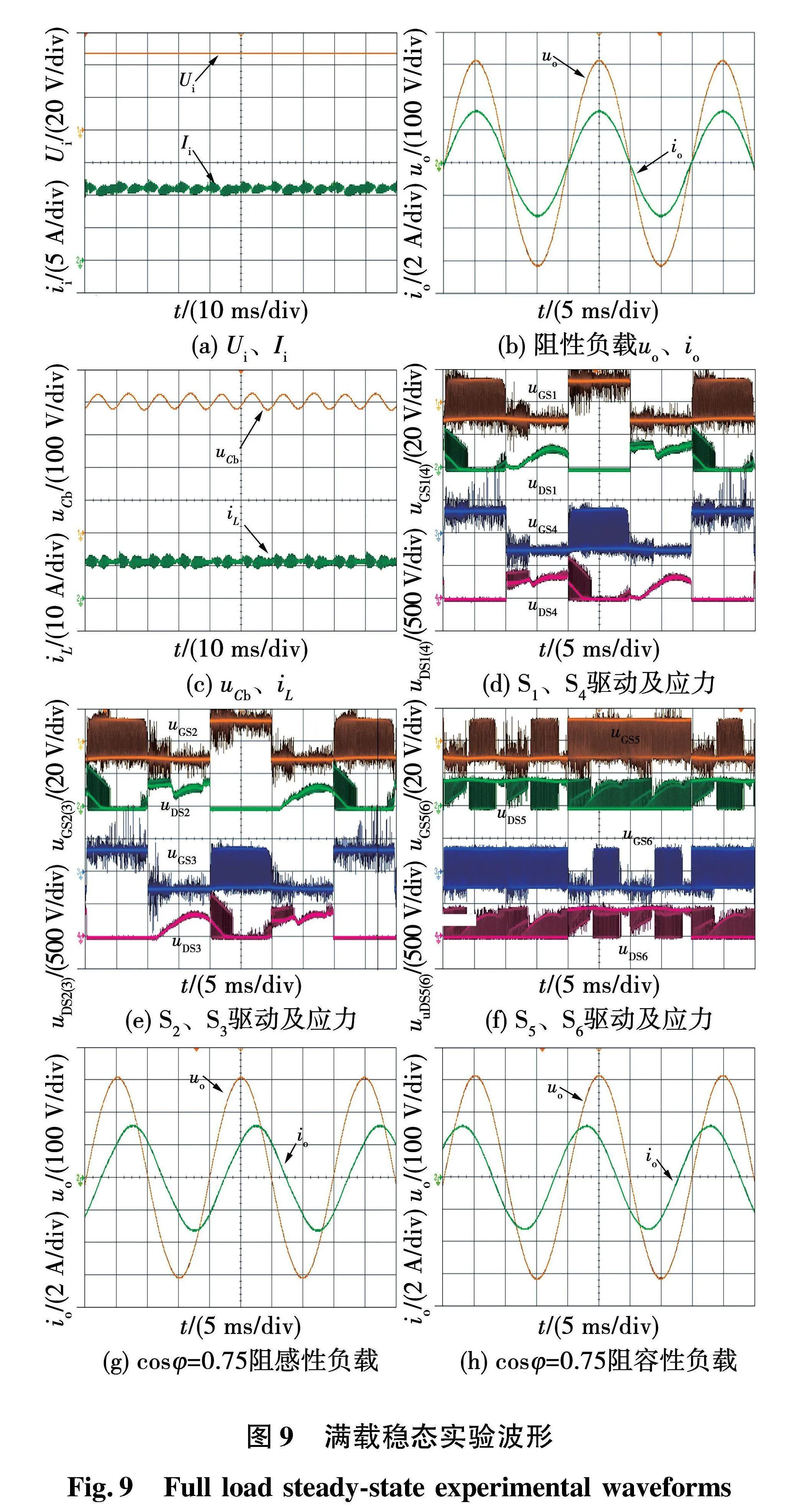
逆变器带阻性、阻感（PF=0.75）及阻容（PF=0.75）满载时的稳态波形如图9所示。

1）由图9（a）可得：输入电流基本在平均值附近高频脉动，二次纹波含量为2.38%，表明二次纹波能得到有效抑制。2）由图9（b）可得：输出电压约220 V，输出电流约为2.3 A，阻性负载下的输出电压THD为3%，波形质量较好，实现了升压逆变。3）由图9（c）可得：在逆变器正常工作时，缓冲电容电压稳定在400 V并呈二倍脉动，储能电感电流在参考值附近脉动，约为11.7 A，与理论分析和仿真一致。4）由图9（g）、图9（h）可得：逆变器能驱动不同负载，适应能力较强，由于实际电感值、电容值及DSP产生占空比的误差，电容电压及电感电流脉动量略大于设计值。5）由图9（d）～图9（f）可得：在输出电压正半周阶段，开关S1、S4互补，轮流作为常通管；输出电压负半周阶段，开关S2、S3互补，轮流作为常通管；有源缓冲电路左、右桥臂轮流给L充磁，与仿真一致。

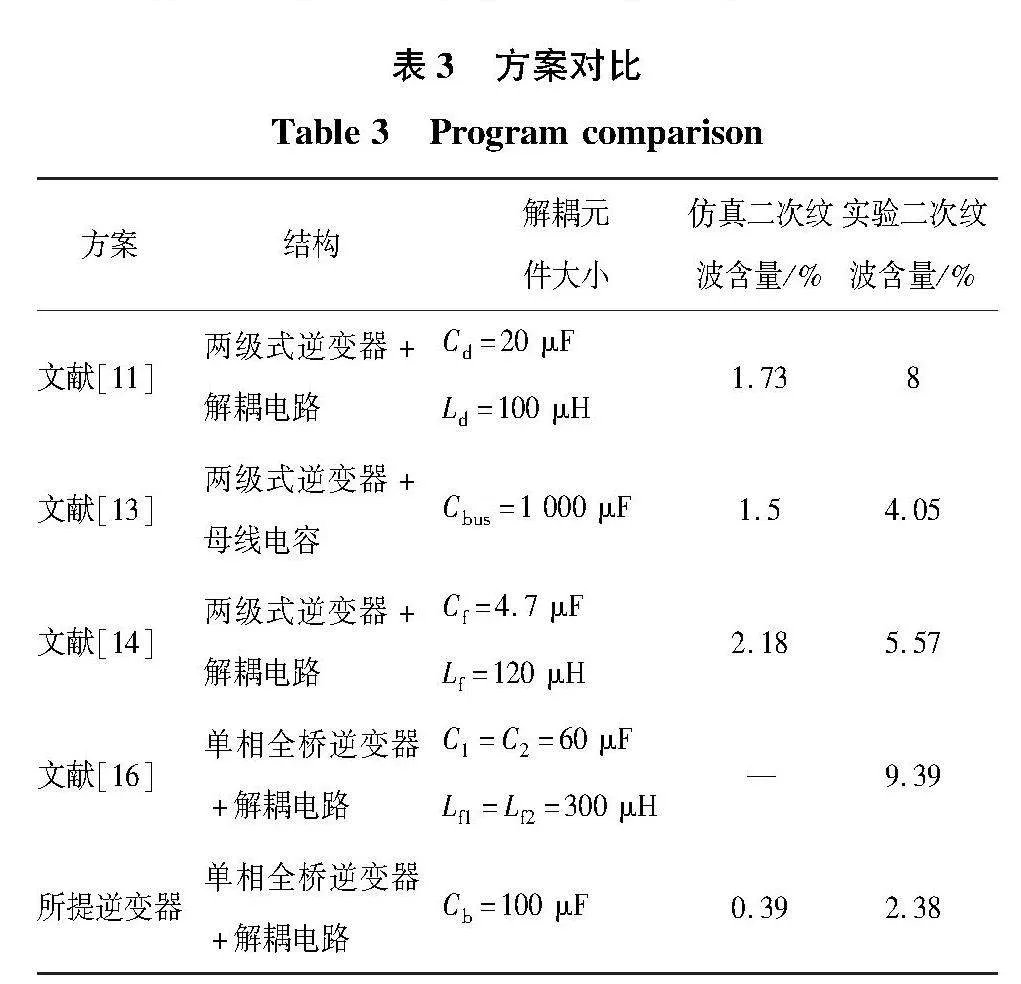
最后从电路结构、解耦元件大小、仿真和实验二次纹波含量几个方面将所提方案与部分引用文献中采用的方案进行了比较，如表3所示。

由表3可知，所提方案采用解耦元件个数最少、参数较小，其仿真波形的输入电流二次纹波含量为0.39%，阻性满载实验时输入电流二次纹波含量为2.38%，具有最好的输入电流二次纹波抑制效果。

7" 结" 论

1）提出了由储能电感、有源缓冲电路和单相电流型逆变桥及滤波器构成的单相逆变器电路拓扑。有源缓冲电路为逆变器能量回馈和输入输出功率解耦提供了硬件条件，实现了单级升压逆变和输入电流二次纹波抑制，解决了电流型逆变器降压阶段储能电感的去磁问题。

2）提出了两模态调制策略和三模态调制策略，设计了2种调制策略下的MPC控制策略，对比分析了2种调制下低频稳态储能电感电流变化规律，得出三模态调制下二次纹波分量与储能电感电流脉动量更低的结论，2种调制策略下的仿真结果证实了这一结论。

3）设计并研制了三模态调制下基于MPC控制的逆变器实验装置，实验结果表明，该逆变器具有较好的输入电流二次纹波抑制能力，输出电压THD较低，为3%，能适应阻性、阻感性和阻容性等各种类型负载。

参 考 文 献：

［1］" REVATHI B S， MAHALINGAM P， GONZALEZ-LONGATT F. Interleaved high gain DC-DC converter for integrating solar PV source to DC bus［J］. Solar Energy，2019，188：924.

［2］" 马钊，张恒旭，赵浩然，等.双碳目标下配用电系统的新使命和新挑战［J］.中国电机工程学报，2022，42（19）：6931.

MA Zhao， ZHANG Hengxu， ZHAO Haoran， et al. New mission and challenge of power distribution and consumption system under dual-carbon target［J］. Proceedings of the CSEE， 2022， 42（19）： 6931.

［3］" 李俊波，闫鹏，魏业文，等.一种新型SEPIC可拓展高增益DC-DC变换器［J］.电机与控制学报，2023，27（4）：64.

LI Junbo， YAN Peng， WEI Yewen， et al. Study on SEPIC expandable step-up DC-DC converter［J］. Electric Machines and Control，2023，27（4）：64.

［4］" 林国庆，何恩义.一种低输入电流纹波高增益软开关DC-DC变换器［J］.电机与控制学报，2023，27（5）：65.

LIN Guoqing， HE Enyi. Low input current ripple high gain soft switching DC-DC converter［J］. Electric Machines and Control，2023，27（5）：65.

［5］" 马小勇，王议锋，王萍，等.燃料电池用交错并联型Boost变换器参数综合设计方法［J］.电工技术学报，2022，37（2）：397.

MA Xiaoyong， WANG Yifeng， WANG Ping， et al. Comprehensive parameter design method of interleaved boost converter for fuel cell applications［J］. Transactions of China Electrotechnical Society，2022，37（2）：397.

［6］" XU S， CHANG L， SHAO R. Single-phase voltage source inverter with voltage boosting and power decoupling capabilities［J］. IEEE Journal of Emerging and Selected Topics in Power Electronics， 2020， 8（3）： 2977.

［7］" NIE L， ZHU G， LUO B， et al. A novel control method for the active power decoupling module with plug-and-play in single phase inverter［C］//2018 IEEE International Power Electronics and Application Conference and Exposition （PEAC）， November 4-7， 2018， Shenzhen， China. 2018：1-6.

［8］" CHRISTIDISG C， NANAKOS A C， TATAKIS E C. Hybrid discontinuous/boundary conduction mode of flyback microinverter for AC-PV modules［J］. IEEE Transactions on Power Electronics， 2016， 31（6）： 4195.

［9］" 陈艳，曹展豪，胡磊，等.准Z源逆变器中抑制二次谐波电流的虚拟阻抗控制策略［J］.电机与控制学报，2023，27（6）：137.

CHEN Yan， CAO Zhanhao， HU Lei， et al. Virtual impedance control strategy for suppressing second harmonic current in quasi-Z-source inverter［J］. Electric Machines and Control，2023，27（6）：137.

［10］" 董帅，林晨，张千帆，等.一种抑制三相准开关升压逆变器电感电流纹波的空间矢量调制方法［J］.电工技术学报，2022，37（17）：4466.

DONG Shuai， LIN Chen， ZHANG Qianfan， et al. A novel space vector modulation method for three-phase quasi-switched-boost inverter to minimize inductor current ripple［J］. Transactions of China Electrotechnical Society，2022，37（17）：4466.

［11］" 章勇高，付伟东，刘鹏，等.一种新型逆变器交流侧功率解耦电路及其控制策略［J］.中国电机工程学报，2020，40（22）：7440.

ZHANG Yonggao， FU Weidong， LIU Peng， et al. Study on a novel AC-side power decoupling circuit of inverter and its control strategy［J］. Proceedings of the CSEE，2020， 40（22）： 7440．

［12］" XU S， CHANG L， SHAO R， et al. Single-phase bridge inverter with active power decoupling based on buck-boost converter［C］//2018 IEEE Energy Conversion Congress and Exposition （ECCE）， September 23-27， 2018， Portland， OR， USA. 2018： 6725-6732.

［13］" ZHU G， RUAN X， ZHANG L， et al. On the reduction of second harmonic current and improvement of dynamic response for two-stage single-phase inverter［J］. IEEE Transactions on Power Electronics， 2015， 30（2）：1028.

［14］" 孙瑞东，曾国宏，王静，等.两级式单相逆变器的二次功率解耦控制［J］.电力自动化设备，2023，43（4）：30.

SUN Ruidong， ZENG Guohong， WANG Jing， et al. Decoupling control of second-harmonic power for two-stage single-phase inverter［J］.Electric Power Automation Equipment，2023，43（4）：30.

［15］" XU S， CAO B， CHANG L， et al. Pulse energy modulation for a single-phase bridge inverter with active power decoupling capability［J］. IEEE Journal of Emerging and Selected Topics in Power Electronics，2020，9（2）：2014.

［16］" 彭寥廓，陈艳慧.单相全桥离网逆变器输出侧功率解耦电路研究［J］.电气技术，2022，23（1）：42.

PENG Liaokuo， CHEN Yanhui. Research on a single-phase full-bridge off-grid inverter with active power decoupling circuit at output side［J］. Electrical Engineering，2022，23（1）：42.

［17］" ZHANG Y， HUANG Y， FANG P， et al. Capacitors voltage ripple complementary control on three-level boost fed single-phase VSI with enhanced power decoupling capability［J］. IEEE Transactions on Power Electronics，2021，36（12）：14220.

（编辑：邱赫男）