三相PWM整流器离散空间矢量无模型预测电流控制策略

摘" 要：

针对PWM整流器模型预测控制对系数参数准确性高度依赖的问题，提出一种基于离散空间矢量的无模型预测电流控制（MFPCC）策略。该策略通过矢量合成，在每个控制周期应用两个基本矢量，提高了预测电流的准确性；通过峰谷采样，分别测量并存储上一控制周期两个基本矢量作用下的电流梯度；并建立电流梯度方程，从而根据应用矢量的电流梯度进一步更新剩余6个未应用矢量的电流梯度，结合当前时刻的电流采样值，实现未来时刻的电流预测，得到下一时刻最优的虚拟矢量。该方法不依赖于任何系统参数，且消除了传统MFPCC策略中电流梯度更新停滞现象，降低了输出电流谐波。最后，通过实验和仿真验证了所提方法的有效性和优越性。

关键词：PWM整流器；无模型预测电流控制；离散空间矢量；电流梯度更新；停滞现象

DOI：10.15938/j.emc.2024.06.016

中图分类号：TM464

文献标志码：A

文章编号：1007-449X（2024）06-0163-08

收稿日期： 2022-09-15

基金项目：新能源与储能运行控制国家重点实验室开放基金（NYB51202201697）

作者简介：胡存刚（1979—），男，教授，博士生导师，研究方向为多电平逆变器的分析与控制；

尹" 政（1996—），男，硕士，研究方向为变流器的调制与控制；

张" 悦（1991—），女，硕士，高级工程师，研究方向为新能源并网控制与仿真；

罗" 魁（1989—），男，硕士，高级工程师，研究方向为新能源并网仿真分析；

芮" 涛（1990—），男，博士，讲师，研究方向为变流器无参数预测控制；

冯壮壮（1998—），男，硕士，研究方向为逆变器模型预测控制。

通信作者：尹" 政

Model-free predictive current control of three-phase PWM rectifier based on discrete space vector

HU Cungang1，2，" YIN Zheng2，" ZHANG Yue1，" LUO Kui1，" RUI Tao3，" FENG Zhuangzhuang2

（1.State Key Laboratory of Operation and Control of Renewable Energy amp; Storage Systems， China Electric Power Research Institute， Beijing 100192， China; 2.School of Electrical Engineering and Automation， Anhui University， Hefei 230601， China; 3.School of Internet， Anhui University， Hefei 230601， China）

Abstract：

Aiming at the problem that the model predictive control of PWM rectifier is highly dependent on the accuracy of system parameters， a model-free predictive current control （MFPCC） strategy based on discrete space vector was proposed. Through vector synthesis， two basic vectors were applied in each control period to improve the accuracy of current prediction; Based on peak and valley sampling， the current gradient of the two applied basic vectors in the previous control period was measured and stored respectively; And by establishing the current gradient equations， so as to further update the current gradient of the remaining 6 non-applied vectors according to the current gradient of the applied vector. The proposed method has strong robustness， and eliminates the stagnation effect in conventional MFPCC， and reduce current harmonics. Finally， effectiveness and advantages of the proposed method are verified by experiment and simulation.

Keywords：PWM rectifier; model-free predictive current control; discrete space vector; current gradient updating; stagnation phenomenon

0" 引" 言

三相脉宽调制（pulse width modulation，PWM）整流器广泛应用在储能、电力传输及交直流微电网分布式发电等工业系统中［1］。为了实现PWM整流器的直流侧输出电压、电网电流和功率因数的控制，已有学者研究了比例积分控制、比例谐振控制和滞环电流控制等方法。然而，这些方法动态响应慢，难以实现多目标的控制。近年来，模型预测电流控制（model predictive current control，MPCC）因其优越的动态性能、良好的多目标控制能力及简单的约束处理等优点［2-3］，在PWM整流器控制领域得到了广泛的关注。然而，MPCC的预测电流由系统模型和参数直接决定，当模型参数失配时，MPCC的控制性能会显著降低［4-6］。

为了消除模型和参数的影响，基于电流梯度的无模型预测电流控制（model-free predictive current control，MFPCC）得到了诸多学者的关注［7-10］。该方法通过测量变流器矢量作用下的电流梯度值替代传统的预测模型［7］。值得注意的是，MFPCC的控制性能会受电流梯度更新频率的影响。当每个控制周期仅通过电流测量，更新应用矢量作用下的电流梯度，而未考虑其他未应用矢量的电流梯度时，会导致PWM的输出电流存在电流尖峰。

为了提高电流梯度的更新频率，文献［8］在控制中设置了更新频率。在该方法中，如果某个电流梯度在50个控制周期内没有被更新，它对应的矢量将在下一个控制周期被使用，其电流梯度也会被随之更新。然而，这种方法会频繁的使用非最优矢量，从而降低电流性能。文献［9］利用过去3个控制周期获得的电流梯度对剩余的梯度进行更新。然而，该方法只有在过去3个控制周期应用的矢量不同时才会生效。文献［10］根据矢量幅值更新剩余矢量的电流梯度。文献［11］简化了数学模型，建立了连续两个控制周期的电流梯度关系，并根据此关系更新剩余矢量的电流梯度。然而，该方法在连续两个周期应用的矢量相同时会失效。

传统MFPCC的另一个问题是每个控制周期仅使用变换器的一个基本矢量，导致开关频率较低，电流纹波较大。为了解决这个问题，文献［12-13］提出了基于虚拟矢量的MFPCC，每个虚拟矢量由2个或3个基本矢量合成。为了获得每个基本矢量作用下的电流梯度，这些方法需要在一个控制周期内根据每个矢量的作用时间进行多次采样，其增加了控制系统的复杂性。此外，这些方法每个控制周期仅更新应用矢量的电流梯度，电流梯度的更新频率较低。

本文针对三相PWM整流器提出一种基于离散空间矢量（discrete space vector，DSV）的改进MFPCC方法。该方法在每个控制周期应用2个基本矢量，可以有效降低电流纹波和THD。此外，提出一种改进的电流梯度更新方法，完全消除传统方法停滞现象及其导致的电流尖峰。在所提的更新方法中，建立电流梯度方程组，可以计算获得应用虚拟矢量对应的2个基本矢量的电流梯度；并根据这2个电流梯度更新剩余6个未应用基本矢量的电流梯度。

1" 传统三相PWM整流器MFPCC

1.1" 三相PWM整流器数学模型

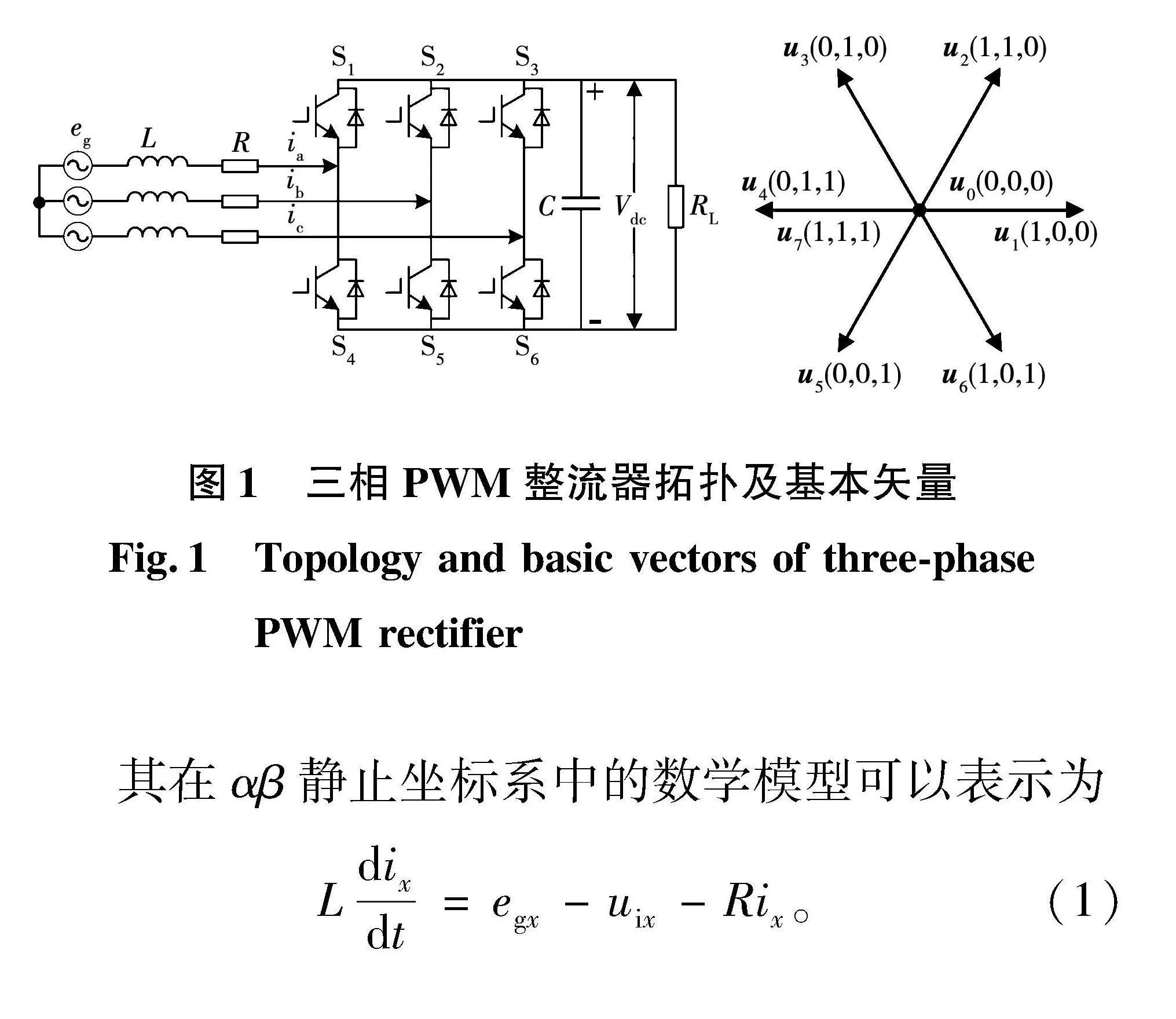
图1给出了典型的三相PWM整流器拓扑结构及其产生的8个基本矢量。

其在αβ静止坐标系中的数学模型可以表示为

Ldixdt=egx－uix－Rix。（1）

式中：x∈{α，β}，uix为αβ坐标系下的逆变器输出电压矢量；ix为αβ坐标系下的逆变器输出电流矢量；egx为αβ坐标系下的电网电压矢量；L为滤波电感；R为滤波电感上的寄生电阻。根据前向欧拉法，式（1）可以离散为

ix（k+1）=ix（k）+TsL［egx（k）－uix（k）－Rix（k）］Δix（k）。（2）

式中：Ts为控制周期；Δix（k）为电压矢量uix（k）作用下的电流梯度。根据式（2）可以得知，MPCC的电流预测依赖于逆变器参数的准确性。然而，逆变器的参数可能因测量误差而不准确，或因工作条件的变化而变化。这种参数的不确定性会导致电流预测误差，降低电流性能。

1.2" 传统MFPCC基本原理

为了消除模型参数对MPCC的影响，有的学者提出了基于电流梯度的MFPCC控制方法［7］，该方法利用采样得到的电流数据替代了传统的预测模型。其中式（2）中的电流梯度可以改写为

Δix（k－1）=ix（k）－ix（k－1）。（3）

在MFPCC中，采样获得电流梯度与应用的电压矢量一一对应，并被存储在查询表（look-up table，LUT）中用于电流预测。因此，（k+1）时刻的预测电流可以表示为

ix（k+1）=ix（k）+Δix（k）。（4）

传统的MFPCC方法在每个控制周期只能更新当前电压矢量作用下的电流梯度值，如图2所示，对于未使用的矢量，其对应的电流梯度值则无法更新，这种更新停滞现象将导致预测的不准确性。此外，其在每个控制周期只采用一个电压矢量，导致逆变器开关频率低，输出电流纹波大。

2" 基于离散空间矢量的MFPCC

为了解决上述问题，本文提出了一种改进的DSV-MFPCC，所提方法包括4个部分：DSV-MFPCC的基本原理、电流梯度更新方法、停滞消除及所提DSV-MFPCC的实现过程。

2.1" DSV-MFPCC基本原理

根据伏秒平衡原理，使用8个基本矢量生成12个虚拟矢量，并表示为

usi=0.5um+0.5un。（5）

式中：usi为电压矢量组合，i∈{1，2，…，12}，12个电压矢量组合分别由（u0，u1）、（u7，u2）、（u0，u3）、（u7，u4）、（u0，u5）、（u7，u6）、（u1，u2）、（u2，u3）、（u3，u4）、（u4，u5）、（u5，u6）、（u6，u1）合成；um和un为2个基本电压矢量。

所提方法在每个控制周期应用两个基本电压矢量。基于所选虚拟矢量对应的电流梯度及其作用时间，可以计算出预测电流。因此，（k+1）时刻和（k+2）时刻的预测电流可以分别表示为：

ix（k+1）=ix（k）+0.5（Δiumx（k）+Δiunx（k））;（6）

ix（k+2）=ix（k+1）+0.5（Δiumx（k+1）+Δiunx（k+1））。（7）

在执行MFPCC时，需要将12个虚拟矢量对应的电流梯度代入式（7），并将得到12个预测电流代入下式所示的价值函数进行评估，最终选择使价值函数最小的电压矢量作为最优电压矢量，并将其作用在下一个控制周期：

G=（irefα－iα（k+2））2+（irefβ－iβ（k+2））2。（8）

式中下标“ref”代表电流的参考值。

2.2" 电流梯度更新方法

当（k-1）时刻和k时刻应用的虚拟矢量由2个基本矢量um和un组成时，如图3所示，由于其作用时间均为0.5Ts，可以在每个控制周期的中点和末端设置两个采样点，分别测量电流梯度Δimx（k-1）和Δinx（k-1）并分别表示为：

Δimx（k－1）=2（ix（k）12－ix（k－1））;

Δinx（k－1）=2（ix（k）－ix（k）12）。（9）

此外，为了更新剩余6个矢量对应的电流梯度，需要建立其与上述2个应用矢量电流梯度之间的关系。根据式（2）可以将剩余矢量作用下的电流梯度Δiyx（k-1）表示为

Δiyx（k－1）=TsL［egx（k－1）－uyx（k－1）－

Rix（k－1）］。（10）

式中：uyx为剩余的6个矢量；Δiyx为剩余矢量对应的电流梯度，其中y≠m和n。

同理，2个应用矢量作用下的电流梯度Δim，nx（k-1）也可以表示为

Δim，nx（k－1）=TsL［egx（k－1）－um，nx（k－1）－

Rix（k－1）］。（11）

式中：um，nx为应用矢量um或un；Δim，nx（k-1）为电流梯度Δimx（k-1）或Δinx（k-1）。

将式（10）和式（11）相减可以得到

Δiyx（k－1）－Δim，nx（k－1）=TsL（um，nx（k－1）－uyx（k－1））。（12）

为了消除式（12）中的电感参数，Δiyx（k-2）和Δim，nx（k-2）之间的关系可以同理表示为

Δiyx（k－2）－Δim，nx（k－2）=TsL（um，nx（k－2）－uyx（k－2））。（13）

将式（12）和式（13）相除可以得到剩余电流梯度更新公式，并表达为

Δiyx（k－1）=um，nx（k－1）－uyx（k－1）um，nx（k－2）－uyx（k－2）×

（Δiyx（k－2）－Δim，nx（k－2））+

Δim，nx（k－1）。（14）

2.3" 电流梯度停滞消除

根据式（14）可知，电流梯度的计算会受公式分母数值的影响。本节从以下两种情形分析剩余梯度的更新情况。

情形1：当式（14）的分母不为0时，其可以进一步化简为

Δiyx（k－1）=（Δiyx（k－2）－Δim，nx（k－2））+

Δim，nx（k－1）。（15）

情形2：当式（14）的分母趋近于0时，电流梯度的更新将不再生效。

以下8种情况可能导致其分母为0，分别为u0β=u1β，u2β=u3β，u4β=u7β，u5β=u6β，u0αβ=u7αβ，u1β=u4β，u3α=u5α和u6α=u2α，如图4所示。根据式（12）可知，相同的坐标分量（即uy（k-1）um，n（k-1））会使电流梯度相同（即Δiy（k-1）=Δim，n（k-1）），剩余梯度的更新可以表达为

Δiyx（k－1）=Δim，nx（k－1）。（16）

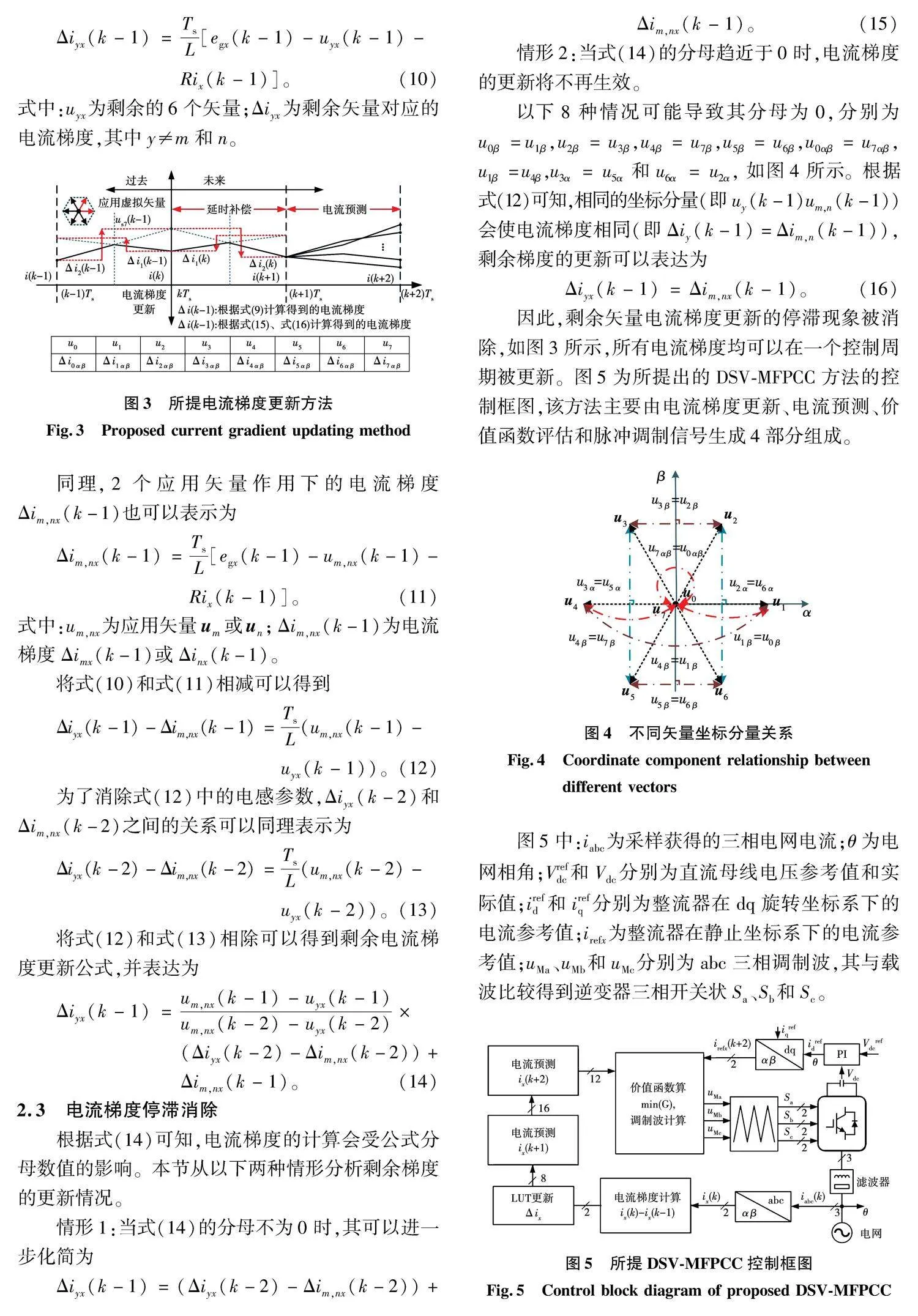
因此，剩余矢量电流梯度更新的停滞现象被消除，如图3所示，所有电流梯度均可以在一个控制周期被更新。图5为所提出的DSV-MFPCC方法的控制框图，该方法主要由电流梯度更新、电流预测、价值函数评估和脉冲调制信号生成4部分组成。

图5中：iabc为采样获得的三相电网电流；θ为电网相角；Vrefdc和Vdc分别为直流母线电压参考值和实际值；irefd和irefq分别为整流器在dq旋转坐标系下的电流参考值；irefx为整流器在静止坐标系下的电流参考值；uMa、uMb和uMc分别为abc三相调制波，其与载波比较得到逆变器三相开关状Sa、Sb和Sc。

3" 仿真和实验验证

3.1" 仿真验证

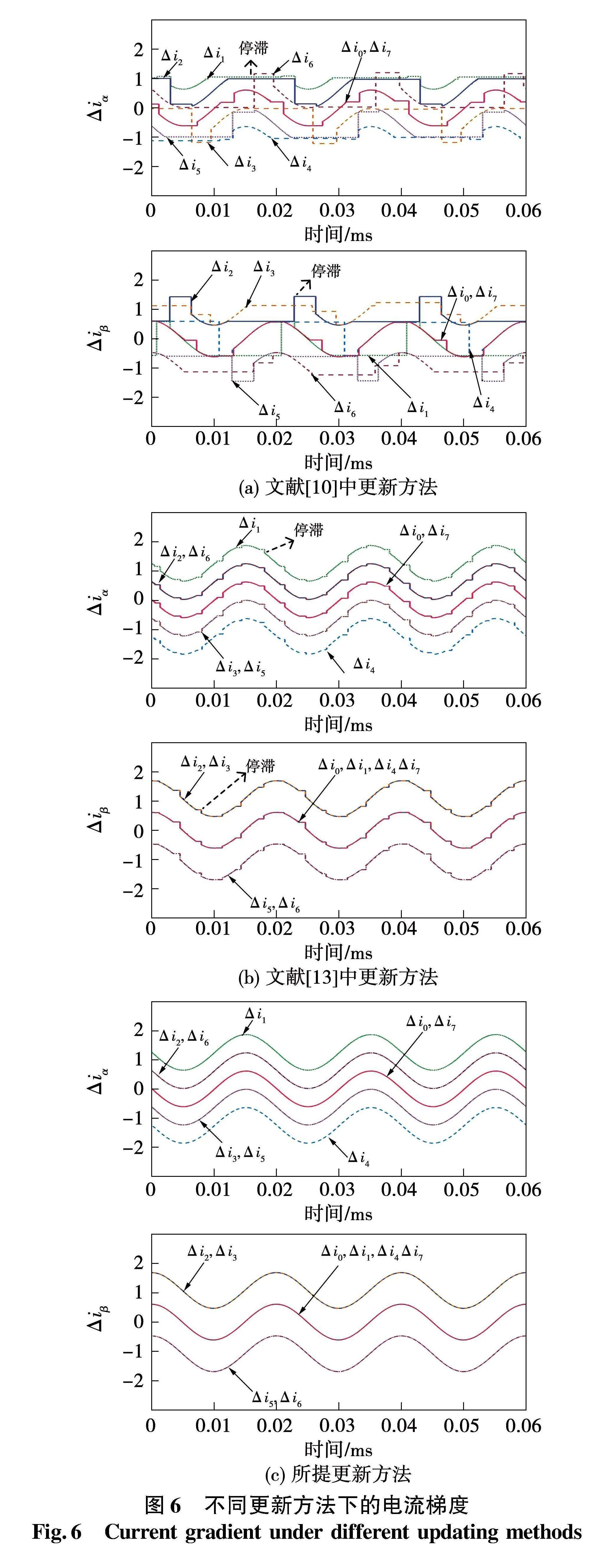
图6为文献［10］中电流梯度更新方法、文献［13］中电流梯度更新方法和所提更新方法的仿真结果。

图6（a）为文献［10］更新方法下的电流梯度波形，在该方法中，每个控制周期仅更新应用电压矢量的电流梯度，而剩余的电流梯度保持上一个控制周期的旧值。如图6（b）所示，当使用文献［13］中的更新方法时，停滞现象减少。然而，Δiα和Δiβ中的停滞现象无法完全消除。图6（c）为所提更新方法的电流梯度波形，可以看出所有电压矢量的电流梯度在每个控制周期都会更新，更新停滞现象完全消除。其中，在α轴中有五条曲线，在β轴中有3条曲线，这是因为Δi2α=Δi6α，Δi3α=Δi5α，Δi0α=Δi7α，Δi2β=Δi3β，Δi5β=Δi6β及Δi0β=Δi7β=Δi4β=Δi1β。

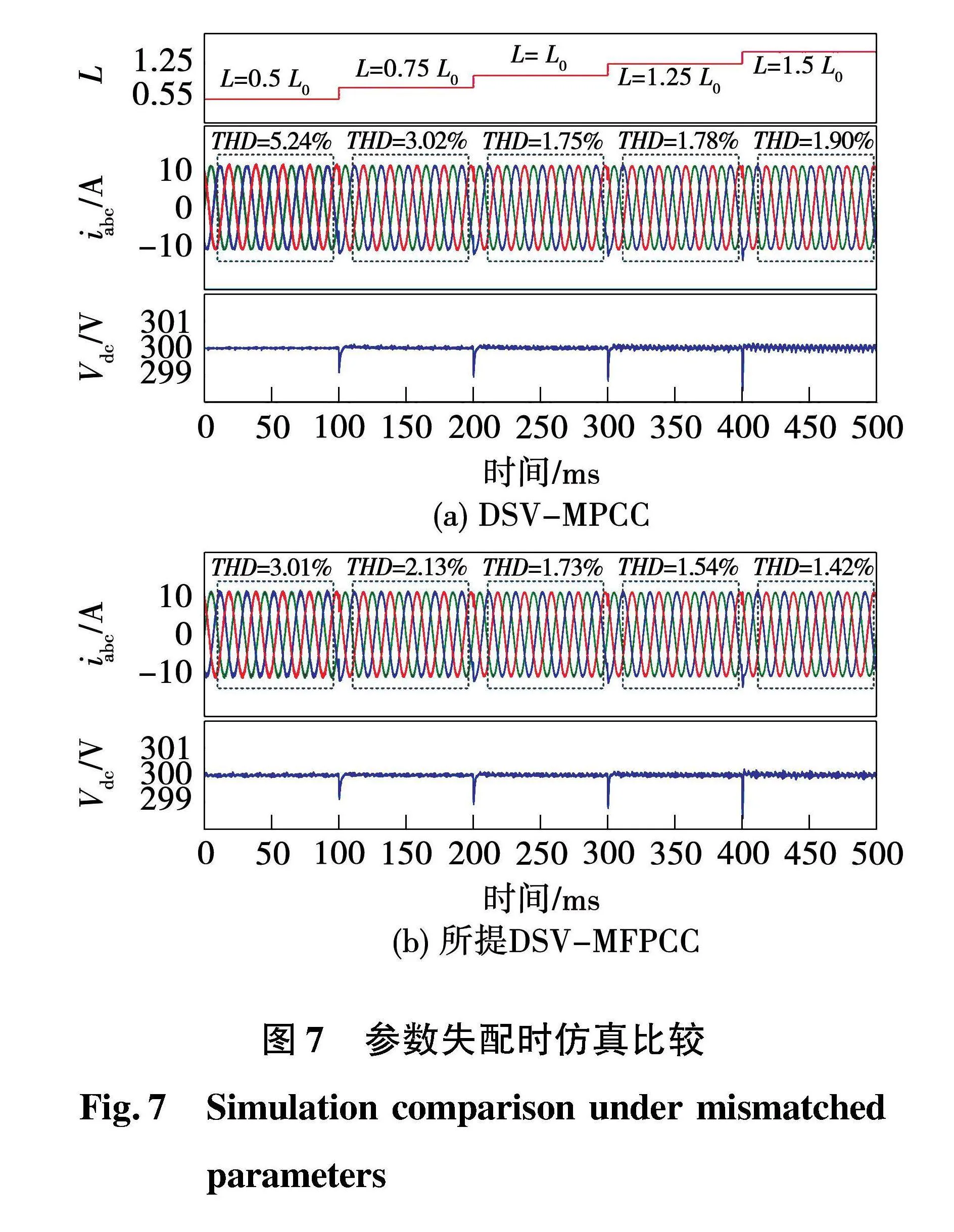
图7为电感实际参数发生变化，控制参数不变时，DSV-MPCC和所提DSV-MFPCC的电流THD及直流侧输出电压仿真结果。由图7（a）可以看出，当电感的实际参数分别为控制参数的50%、75%、125%、150%时，DSV-MPCC的电流THD较参数准确时分别增大199.4%、72.6%、1.7%和8.6%，同时，系统直流侧输出电压纹波变大。如图7（b）所示，所提DSV-MFPCC方法参数鲁棒性较好，在参数失配时电流THD较DSV-MPCC均有所降低，尤其在实际参数为控制参数的50%时。

3.2" 实验验证

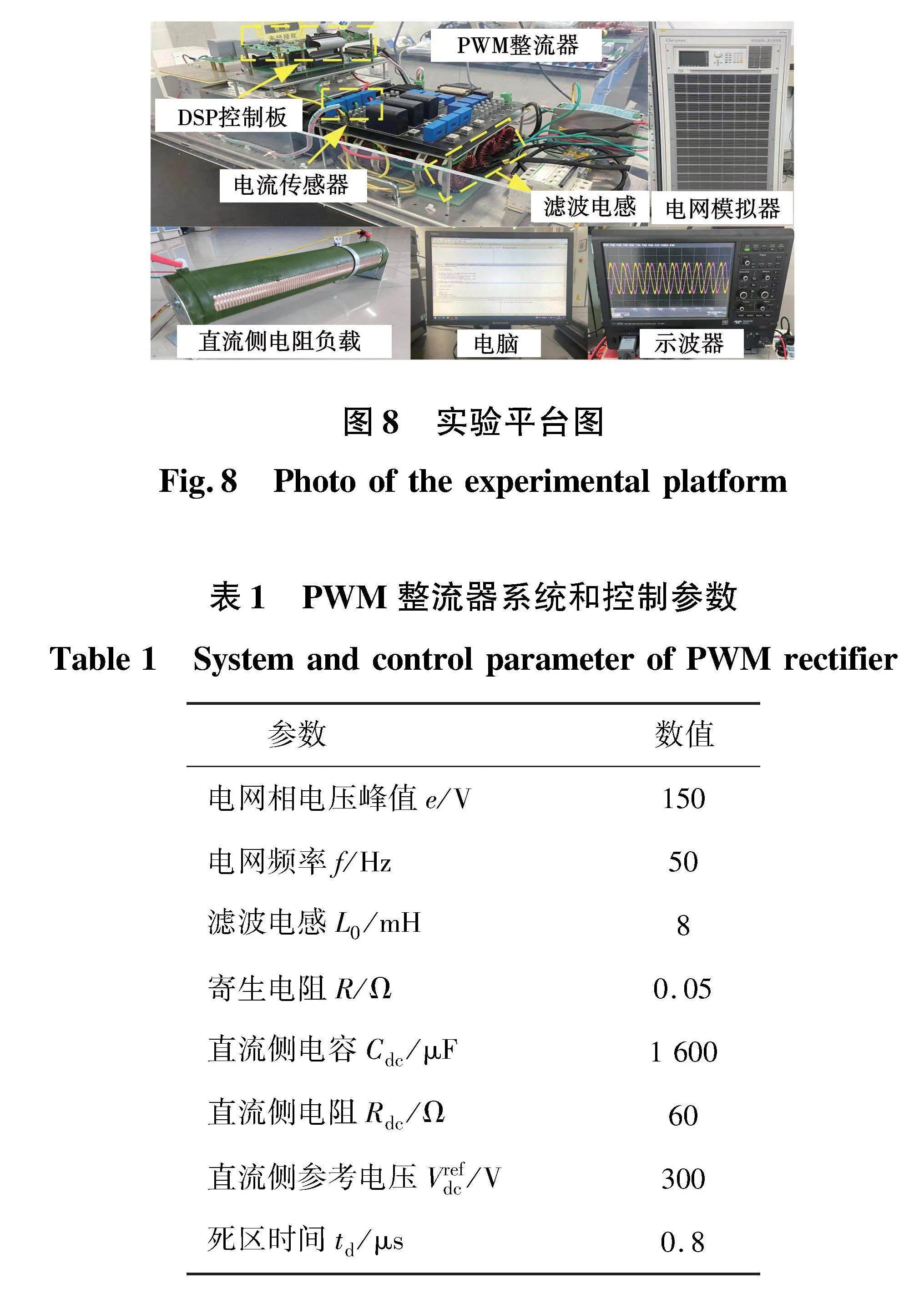
为了验证所提DSV-MFPCC方法的有效性，搭建了两电平PWM整流器实验平台，如图8所示。其包括直流电压源、三相并网逆变器、滤波电感和交流电压源。所有控制方案均在TMS320F28335中实现，系统和控制参数如表1所示。示波器型号为LeCroy-HDO4034。电流探头型号为LeCroy-CP150。

3.2.1" 鲁棒性能验证

图9比较了参数失配时DSV-MPCC和所提DSV-MFPCC的电流纹波、THD、预测误差及直流侧输出电压。由图9（a）可以看出，当电感的控制参数突变为实际参数的50%时，DSV-MPCC的输出电流纹波、THD、电流预测误差及直流侧输出电压纹波均变大，其中THD由3.58%增加为4.72%；当电感的控制参数突变为实际参数的2倍时，DV-MPCC输出性能也随之变差，其中THD由3.58%增加为6.83%。如图9（c）所示，所提DSV-MFPCC方法输出性能不受参数的影响，THD保持为3.56%，与DSV-MPCC在两种失配条件下的THD相比分别降低了1.14%及3.25%。3种方法的THD频谱如图10所示，验证了所提方法具有良好的参数鲁棒性。

3.2.2" 电流梯度更新验证

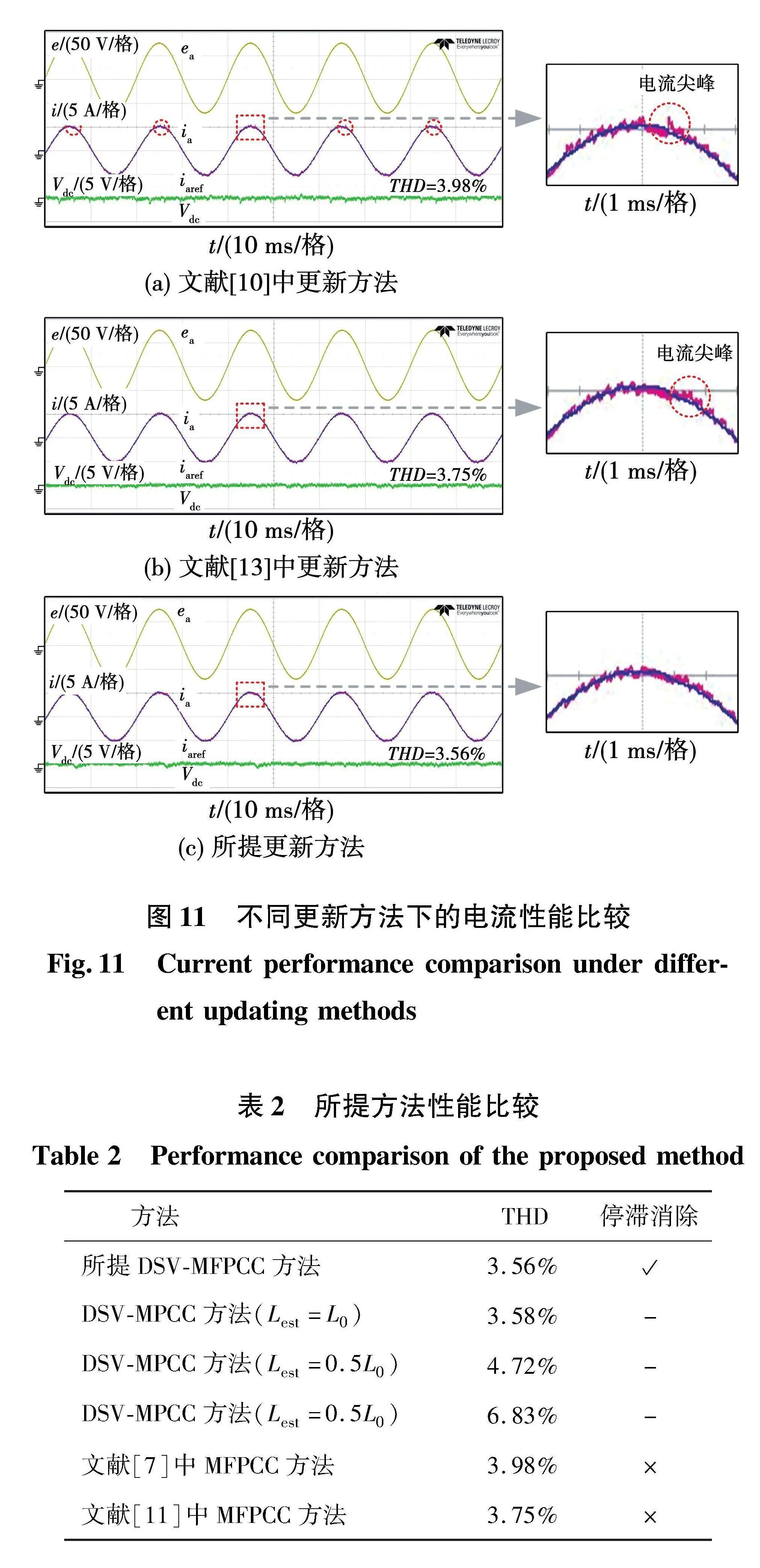
为了有效的比较电流梯度停滞现象对电流性能的影响，文献［7］和文献［11］中的更新方法被应用在离散空间矢量的条件下并与所提更新方法进行比较。如图11（a）所示，由于文献［7］中的更新方法存在明显的停滞现象，导致电流纹波和直流电压纹波存在较多的电流尖峰。如图11（b）所示，当使用文献［11］中的更新方法时，虽然电流尖峰被有效改善，但由于停滞现象没有完全消除，电流尖峰仍然存在。与文献［7］和文献［11］的更新方法相比，所提方法完全消除了停滞现象，因此其电流纹波和直流侧电压纹波最低，验证所提更新方法的有效性。所提方法的性能比较如表2所示。

3.2.3" 动态性能验证

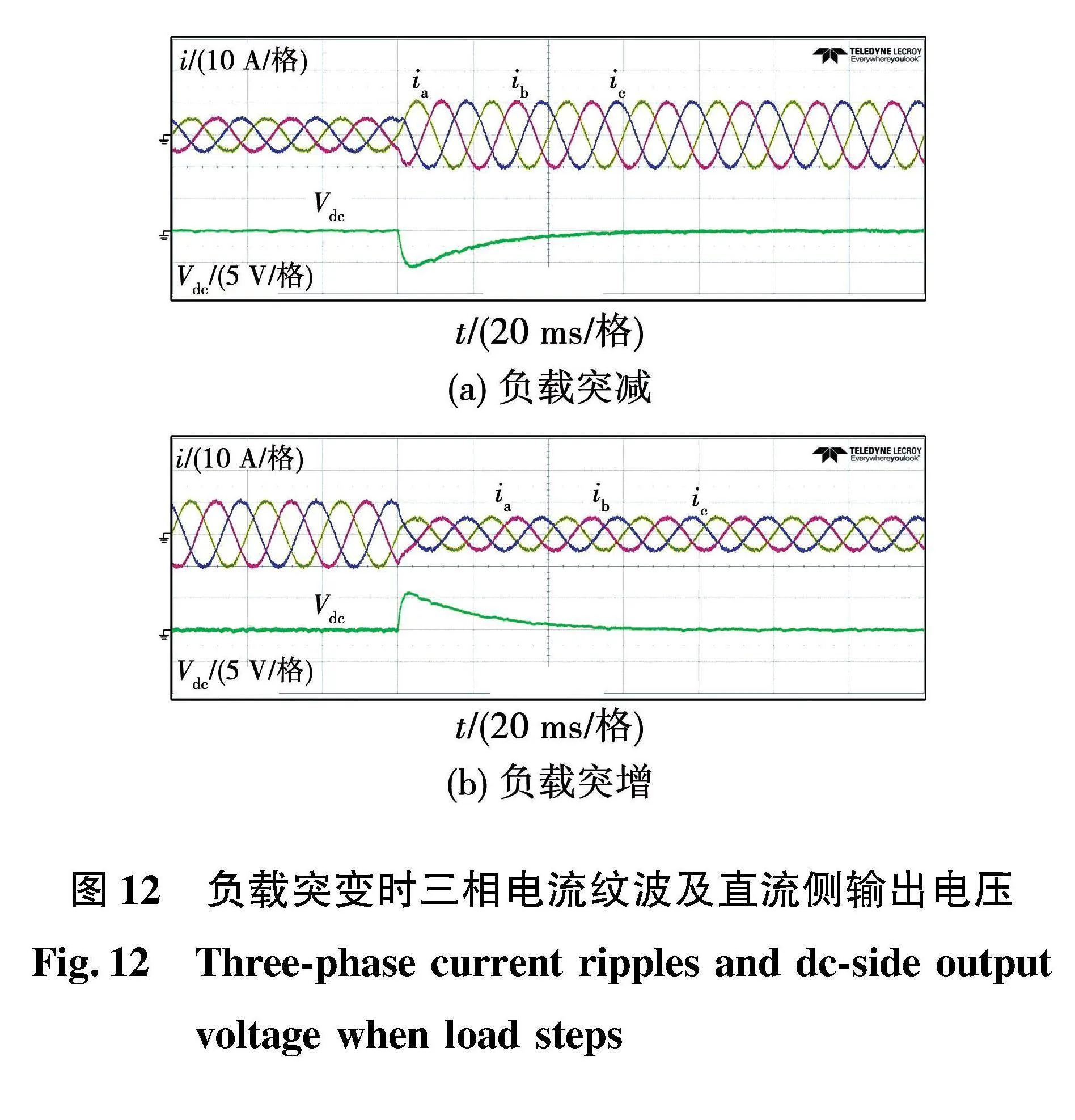
图12给出了所提方法在负载突变下的三相电流及直流侧输出电压波形，突减负载由120 Ω突变为60 Ω，突加负载由60 Ω突变为120 Ω。由图12（a）可以看出，负载突减时，直流电压调节时间为63 ms，电压跌落为2%；由图12（b）可以看出，负载突增时，直流电压调节时间为59 ms，电压超调为2.5%。

4" 结" 论

本文提出了一种基于电流梯度全更新的离散空间矢量MFPCC方法，并在三相并网逆变器平台实验测试。结果表明，所提方法具有以下优点：

1） 该方法在每个控制周期内使用两个电压矢量，减小了输出电流的纹波和THD。

2） 它不依赖于任何模型参数，具有良好的参数鲁棒性，并在参数准确的条件下实现了与离散空间矢量MPCC相近的控制性能。

3） 该方法提出了一种先进的电流梯度更新方法，完全消除了电流梯度停滞现象及其导致的电流尖峰，进一步改善了电流质量。

后续研究可以通过改进矢量组合实现双矢量、三矢量MFPCC控制，进一步减小电流纹波；或将其应用于LCL滤波的PWM整流器中，进一步研究高阶系统下的参数鲁棒性问题。

参 考 文 献：

［1］" 王占扩，张永昌，童朝南.一种改进的三相PWM整流器模型预测控制方法研究［J］.电机与控制学报，2020，24（7）：73.

WANG Zhankuo， ZHANG Yongchang， TONG Chaonan. Improved model predictive direct power control for three-phase PWM rectifier ［J］. Electric Machine and Control，2020，24（7）：73.

［2］" 郭磊磊，金楠，许烈.采用混合电压矢量预选和参考电压预测的逆变器共模电压尖峰消除方法［J］.中国电机工程学报，2018，38（17）：5167.

GUO Leilei， JIN Nan， XU Lie. Common-mode voltage spikes elimination method for inverters using hybrid voltage vector preselection and reference voltage prediction ［J］. Proceedings of the CSEE， 2018， 38（17）： 5167.

［3］" 朱文杰，陈昌松，段善旭．一种基于离散空间矢量调制的 Vienna 整流器模型预测控制方法［J］．中国电机工程学报， 2019， 39（20）： 6008．

ZHU Wenjie， CHEN Changsong， DUAN Shanxu． A model predictive control method with discrete space vector modulation of vienna rectifier［J］．Proceedings of the CSEE，2019，39（20）：6008．

［4］" HU Cungang， YIN Zheng， RUI Tao， et al. A novel double-voltage-vector model-free predictive current control method for two-level voltage source inverters［J］. IEEE Transactions on Industrial Electronics， 2023， 70（6）： 5872.

［5］" 胡存刚， 尹政， 芮涛， 等. 计及采样扰动抑制的电压源逆变器三矢量无模型预测电流控制方法［J］. 中国电机工程学报， 2024， 44（6）： 2408.

HU Cungang， YIN Zheng， RUI Tao， et al. Triple-vector model-free predictive current control method for voltage source inverter with sampling disturbance suppression［J］. Proceedings of the CSEE， 2024，44（6）：2408.

［6］" YIN Zheng， DENG Fujin， GHANEM A， et al. PLPR-based predictive control for LCL-filtered voltage source inverters［J］. IEEE Transactions on Power Electronics， 2024， 39（6）： 7468.

［7］" LIN Chengkai， LIU Tianhua， YU Jente， et al. Model-free predictive current control for interior permanent-magnet synchronous motor drives based on current difference detection technique［J］. IEEE Transactions on Industrial Electronics， 2014， 61（2）：667.

［8］" LIN Chengkai， YU Jente， LAI Yenshin， et al. Improved model-free predictive current control for synchronous reluctance motor drives［J］. IEEE Transactions on Industrial Electronics， 2016， 63（6）： 3942.

［9］" CARLET P G， TINAZZI F， BOLOGNANI S， et al. An effective model-free predictive current control for synchronous reluctance motor drives［J］. IEEE Transactions on Industry Applications， 2019， 55（4）： 3781.

［10］" YU Feng， ZHOU Chenhui， LIU Xing， et al. Model-free predictive current control for three-level inverter-fed IPMSM with an improved current difference updating technique［J］. IEEE Transactions on Energy Conversion， 2021，36（4）：3334.

［11］" MA Chenwei， LI Huayu， YAO Xuliang， et al. An improved model-free predictive current control with advanced current gradient updating mechanism［J］. IEEE Transactions on Industrial Electronics， 2021， 68（12）： 11968.

［12］" AGUSTIN C A， YU Jente， CHENG Yushan， et al. Model-free predictive current control for synRM drives based on optimized modulation of triple-voltage-vector［J］. IEEE Access， 2021，9： 130472.

［13］" AGUSTIN C A， YU Jente， LIN Chengkai， et al. Triple-voltage-vector model-free predictive current control for four-switch three-phase inverter-fed SPMSM based on discrete-space-vector modulation［J］. IEEE Access， 2021，9：60352.

（编辑：刘素菊）