DCM升压型PFC变换器的电流重整形补偿策略

摘" 要：

针对不连续导通模式（DCM）下的升压型功率因数矫正（PFC）变换器，对其中的寄生参数致电流失真（PCD）效应进行研究。考虑元器件寄生参数，求解输入电压、输出电压和占空比的全微分方程，得到精确的阻尼型电感电流解析表达式。研究发现，PCD效应会导致很大的电流失真，从而显著降低系统功率因数。为了减小PCD效应，通过在不同条件下推导得到的补偿增益，能将输入电流重整为正弦波。对基于无电流传感的平均电流模式（SACM）控制，提出一种能降低PCD效应的电流重整形补偿策略。该策略对阻尼型电感电流方程进行增益补偿，进而降低电流阻尼导致的PCD效应。最后仿真和实验证明，增益补偿几乎不随负载电阻变化，变换器中的PCD效应和电流重整形策略有效。

关键词：变换器；电流失真；寄生参数效应；电流重整；增益补偿；功率因数

DOI：10.15938/j.emc.2024.06.018

中图分类号：TM46

文献标志码：A

文章编号：1007-449X（2024）06-0181-08

收稿日期： 2022-08-08

基金项目：

作者简介：张" 明（1980—），男，硕士，高级工程师，研究方向为电力电子技术；

罗雷明（1996—），男，硕士研究生，研究方向为功率集成电路设计；

张" 凯（1998—），男，硕士研究生，研究方向为功率集成电路设计；

姜东升（1974—），男，硕士，高级工程师，研究方向为电力电子技术；

张凡武（1968—），男，硕士，研究员级高级工程师，研究方向为电力电子技术；

雷" 鹏（1987—），男，工程师，研究方向为电力电子技术。

通信作者：闵" 闰

Current reconstruction strategy for DCM boost PFC converter

ZHANG Ming1，" LUO Leiming2，" ZHANG Kai2，" JIANG Dongsheng1，" ZHANG Fanwu3，" LEI Peng3，" MIN Run2

（1.Beijing Institute of Spacecraft System Engineering， Beijing 100094， China; 2.School of Optical and Electronic Information， Huazhong University of Science and Technology， Wuhan 430074， China; 3.Technical Center of Dong Motor Corporation， Wuhan 430056， China）

Abstract：

For parasitics-induced current distortion （PCD） effect in discontinuous conduction mode boost power factor correction （PFC） converter， with consideration of parasitics， an accurate damped inductor current equation was derived through the functions of input voltage， output voltage and duty cycle. PCD effect was found to have considerable influence to current distortion， which degraded PF under SACM control. In order to reduce the PCD effect， a compensation gain was derived to reshape the input current. The gain was calculated at different conditions. A current reconstruction strategy was proposed for sensorless average current mode （SACM） control. Based on the damped current equations， a compensation gain was derived to reconstruct the input current， which reduces the current damping and distortion caused by parasitics. It is proved to have little change along load resistance.Both the PCD phenomenon and the current reconstruction strategy are verified by simulations and experiments.

Keywords：converter; current distortion; parasitic effect; reconstructed current; gain compensation; power factor

0" 引" 言

功率因数校正（power factor correction，PFC）变换器广泛使用在工业应用中，它可以减少设备输入电流的谐波失真，提高变换效率。作为常用的拓扑，升压型PFC变换器具有输入电流纹波小，电路结构简单，输入电压范围大的优点［1-2］。

针对不连续导通模式（discontinuous conduction mode，DCM）工作模式，人们提出了多种控制策略，以提高系统功率因数［3-6］。虽然实现固定的占空比非常简单，但这样会导致严重的谐波电流失真，相比之下，平均电流控制模式（average current mode，ACM）能够实现可变占空比，将输入电流重整为正弦波，从而显著提高了功率因数（power factor，PF），为了实现DCM升压PFC变换器下的ACM控制，电流采样需要用到电流感应器和辅助电路。这些组件不仅降低了精度，而且增加了系统功耗和复杂性［7-15］。为了简化电流环路，采用了无电流感应的平均电流模式（sensorless average current mode，SACM），通过这种模式能实现对电感电流的精确控制，且具有电流环路简单，无需电流传感的优点。然而，SACM控制对电感电流模型精度的依赖性较强，因此需要考虑各种寄生参数效应对电感电流的影响。

在SACM控制下的变换器中存在寄生参数致电流失真（parasitics-induced current distortion，PCD）效应。即阻性寄生参数导致的输入电流畸变。 SACM控制器本应将输入电流iin调整为正弦波。然而，实际电流平均值通常呈凹形，降低了功率因数。该现象在实际应用中常常被忽视，且缺乏理论解释。

为了提高SACM控制下的功率因数，解决上述电流凹陷问题，本文提出一种电流重整形补偿策略，对SACM控制器的占空比进行增益补偿，从而抵消寄生参数导致的电流阻尼。

1" SACM控制的DCM升压型PFC变换器

SACM控制下的DCM升压型PFC变换器如图1所示。电路前端是一个全桥整流器，对交流输入进行基本的整流；接着是一个LC低通滤波器，滤除电感电流的高次谐波分量，以平滑输入电流iin。SACM控制器通过动态占空比，把电感电流平均值调整成正弦曲线，从而提高输入功率因数。

在没有电流传感器的情况下，SACM控制器会计算合适的占空比来调节输入电流。由线电压vg、输出电压vo和输入电流幅度Im的参考值推导得出所需的占空比。其中Im由外环PI产生，用于调节输入电流在半线周期内的幅度。

1.1" 可变占空比的SACM控制

SACM控制为了提高功率因数，采用可变占空比将输入电流调节为正弦波。此时的电感电流和所需的占空比如图2所示。在脉冲宽度调制下，变换器的输入电流为

iin（ωt）=d1（ωt）2TVmsin（ωt）2L（1－Vm|sin（ωt）|/vo）。（1）

其中Vm是输入电压的峰值。因而，为了将输入电流调节为正弦波，所需要的占空比为

d1（ωt）=2LIm（1－Vm|sin（ωt）|/vo）TVm。（2）

在上述占空比下，SACM控制可以将电感电流调整正弦波的形式，从而实现最高功率因数。

1.2" SACM控制下的变换器静态分析

基于SACM控制能实现单位1的功率因数。在DCM模式下，变换器在每次开关结束时不存储能量，若不考虑损耗，则输入功率和输出功率是相等的。因此输出电流为

io（ωt）=ImVm|sin（ωt）|2vo。（3）

由于输出电压是io（ωt）R，可求得Im的稳态值

Im=πv2oRVm∫π0|sin（ωt）|2d（ωt）。（4）

将式（4）代入式（2），得到稳态下占空比

d1，ss（ωt）=

voVm2L（1－Vm|sin（ωt）|/vo）RTπ∫π0|sin（ωt）|2d（ωt）12。（5）

上述所有的方程均没有考虑寄生参数，这会引起一定的误差。

2" PCD效应和SACM控制下的电流重整形

基于所提出的阻尼电流方程，推导占空比补偿增益，最终减小PCD效应。

考虑阻性寄生参数，升压型PFC变换器的结构如图3所示。各类阻性寄生参数的含义见表1。其中RC对vo对电流失真的影响可忽略不计。但其他寄生电阻会导致较大的PCD效应。

2.1" DCM升压型PFC变换器的等效电流模型和电流阻尼分析

为了便于分析寄生参数导致的电流失真，图4给出了升压型PFC变换器的等效电路结构。基于状态空间平均，前端的桥和滤波器等效于图4（a）的线性电路，而升压变换器的电路如图4（b）所示。输入量是线电压vg，略低于|vin|。此外，考虑到寄生电阻。通过全微分推导出精确的电感电流。

假设PFC变换器具有单位1的功率因数PF，则升压变换器的输入端也具有纯阻性，等效电阻如下：

Re=vg（ωt）iL_av（ωt）≈VmIm。（6）

因为在全桥中总存在两个导通的二极管，所以vF1和RF1的值会加倍。由于图4（a）等效电路中的寄生参数都很小，导致了零极点位置都很高，因此，在较低的线频率处，由v1到vg的传递函数近似为

|H（jω）|≈Re2RF1+RLin+Re。（7）

继而可得线电压vg（ωt）为

vg（ωt）=|H（jω）|v1=Re（|vin|－2vF1）2RF1+RLin+Re。（8）

阻性寄生参数对电感电流的影响如图5所示。其中：Pdamp1是电感电流的相对阻尼比；Pdamp2是占空比的相对阻尼比；Pdamp3是输出电流平均值的相对阻尼比。

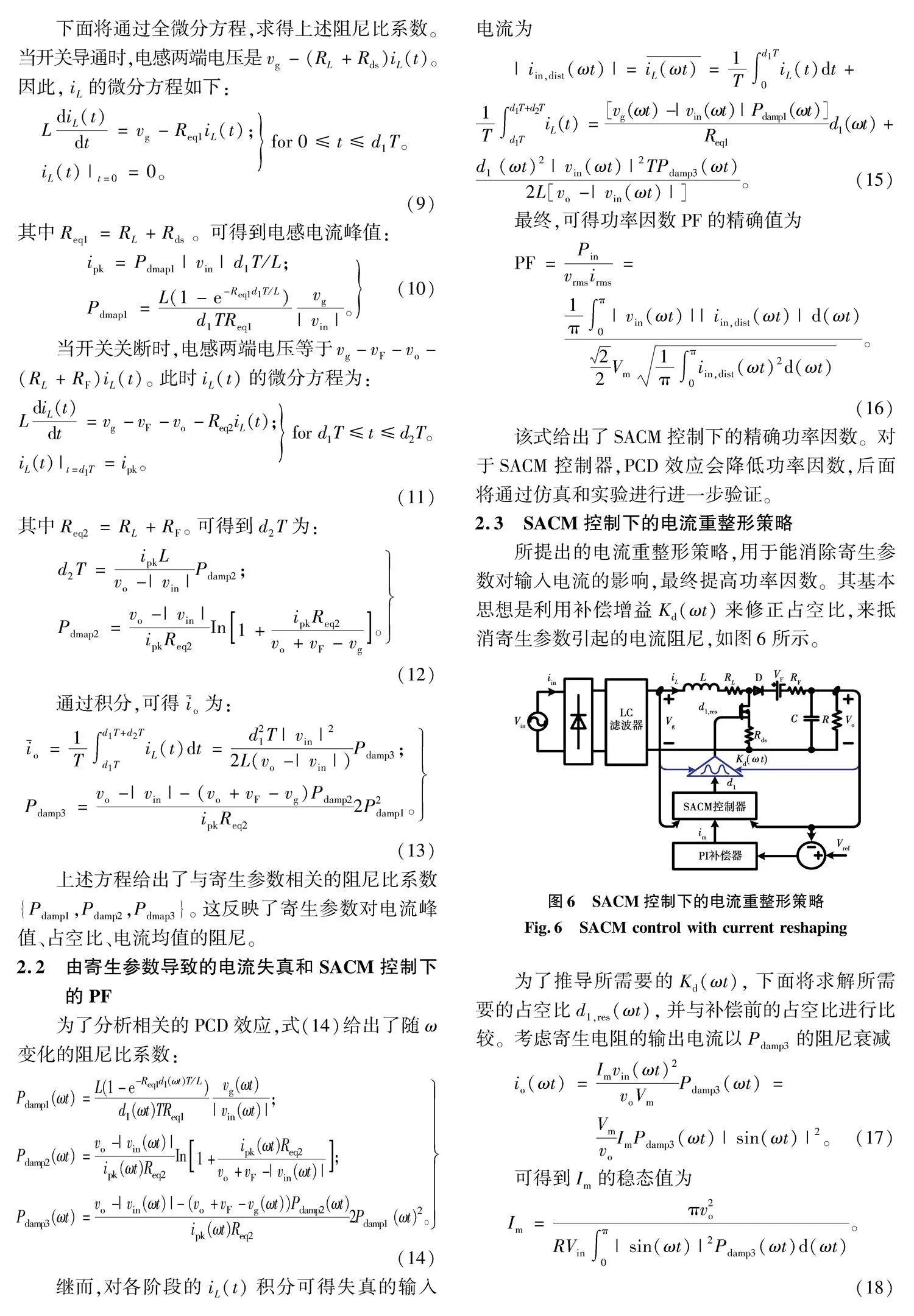
下面将通过全微分方程，求得上述阻尼比系数。当开关导通时，电感两端电压是vg－（RL+Rds）iL（t）。因此，iL的微分方程如下：

LdiL（t）dt=vg－Req1iL（t）；

iL（t）|t=0=0。 for 0≤t≤d1T。（9）

其中Req1=RL+Rds。可得到电感电流峰值：

ipk=Pdmap1|vin|d1T/L；

Pdmap1=L（1－e－Req1d1T/L）d1TReq1vg|vin|。（10）

当开关关断时，电感两端电压等于vg－vF－vo－（RL+RF）iL（t）。此时iL（t）的微分方程为：

LdiL（t）dt=vg－vF－vo－Req2iL（t）；

iL（t）|t=d1T=ipk。 for d1T≤t≤d2T。（11）

其中Req2=RL+RF。可得到d2T为：

d2T=ipkLvo－|vin|Pdamp2；

Pdmap2=vo－|vin|ipkReq2In1+ipkReq2vo+vF－vg。（12）

通过积分，可得i-o为：

i-o=1T∫d1T+d2Td1TiL（t）dt=d21T|vin|22L（vo－|vin|）Pdamp3；

Pdamp3=vo－|vin|－（vo+vF－vg）Pdamp2ipkReq22P2damp1。（13）

上述方程给出了与寄生参数相关的阻尼比系数{Pdamp1，Pdamp2，Pdmap3}。这反映了寄生参数对电流峰值、占空比、电流均值的阻尼。

2.2" 由寄生参数导致的电流失真和SACM控制下的PF

为了分析相关的PCD效应，式（14）给出了随ω变化的阻尼比系数：

Pdamp1（ωt）=L（1－e－Req1d1（ωt）T/L）d1（ωt）TReq1vg（ωt）|vin（ωt）|；

Pdamp2（ωt）=vo－|vin（ωt）|ipk（ωt）Req2In1+ipk（ωt）Req2vo+vF－|vin（ωt）|；

Pdamp3（ωt）=vo－|vin（ωt）|－（vo+vF－vg（ωt））Pdamp2（ωt）ipk（ωt）Req22Pdamp1（ωt）2。（14）

继而，对各阶段的iL（t）积分可得失真的输入电流为

|iin，dist（ωt）|=iL（ωt）=1T∫d1T0iL（t）dt+

1T∫d1T+d2Td1TiL（t）=［vg（ωt）－|vin（ωt）|Pdamp1（ωt）］Req1d1（ωt）+

d1（ωt）2|vin（ωt）|2TPdamp3（ωt）2L［vo－|vin（ωt）|］。（15）

最终，可得功率因数PF的精确值为

PF=Pinvrmsirms=

1π∫π0|vin（ωt）||iin，dist（ωt）|d（ωt）22Vm1π∫π0iin，dist（ωt）2d（ωt）。（16）

该式给出了SACM控制下的精确功率因数。对于SACM控制器，PCD效应会降低功率因数，后面将通过仿真和实验进行进一步验证。

2.3" SACM控制下的电流重整形策略

所提出的电流重整形策略，用于能消除寄生参数对输入电流的影响，最终提高功率因数。其基本思想是利用补偿增益Kd（ωt）来修正占空比，来抵消寄生参数引起的电流阻尼，如图6所示。

为了推导所需要的Kd（ωt），下面将求解所需要的占空比d1，res（ωt），并与补偿前的占空比进行比较。考虑寄生电阻的输出电流以Pdamp3的阻尼衰减

io（ωt）=Imvin（ωt）2voVmPdamp3（ωt）=

VmvoImPdamp3（ωt）|sin（ωt）|2。（17）

可得到Im的稳态值为

Im=πv2oRVin∫π0|sin（ωt）|2Pdamp3（ωt）d（ωt）。（18）

假设d1，res（ωt）可以将|iin，dist（ωt）|调整为Im|sin（ωt）|，则基于式（15）和式（18），可以得到如下形式：

d1，res（ωt）=2ImVmb（ωt）［a（ωt）2+b（ωt）－a（ωt）］；

a（ωt）=［vg（ωt）/Vm|sin（ωt）|－Pdamp1（ωt）/Req1］；

b（ωt）=2TPdamp3（ωt）Im|sin（ωt）|L［vo－Vm|sin（ωt）|］。（19）

最后，将式（19）除以式（5），即可得所需的增益补偿

Kd（ωt）=d1，res（ωt）d1，SS（ωt）。（20）

该增益是随ωt变化的序列，通过微调占空比来抵消PCD效应，将输入电流重整形为正弦波，最终提高功率因数。

3" 仿真

为了验证电流重整形补偿方法的有效性，下面基于MATLAB/Simulink搭建了DCM升压型PFC变换器模型。变换器的主要参数如表2所示。下面将基于这些参数，分别验证考虑寄生电阻和不考虑寄生电阻的2种情况。

3.1" 考虑PCD效应的SACM控制下的输出电流和PF

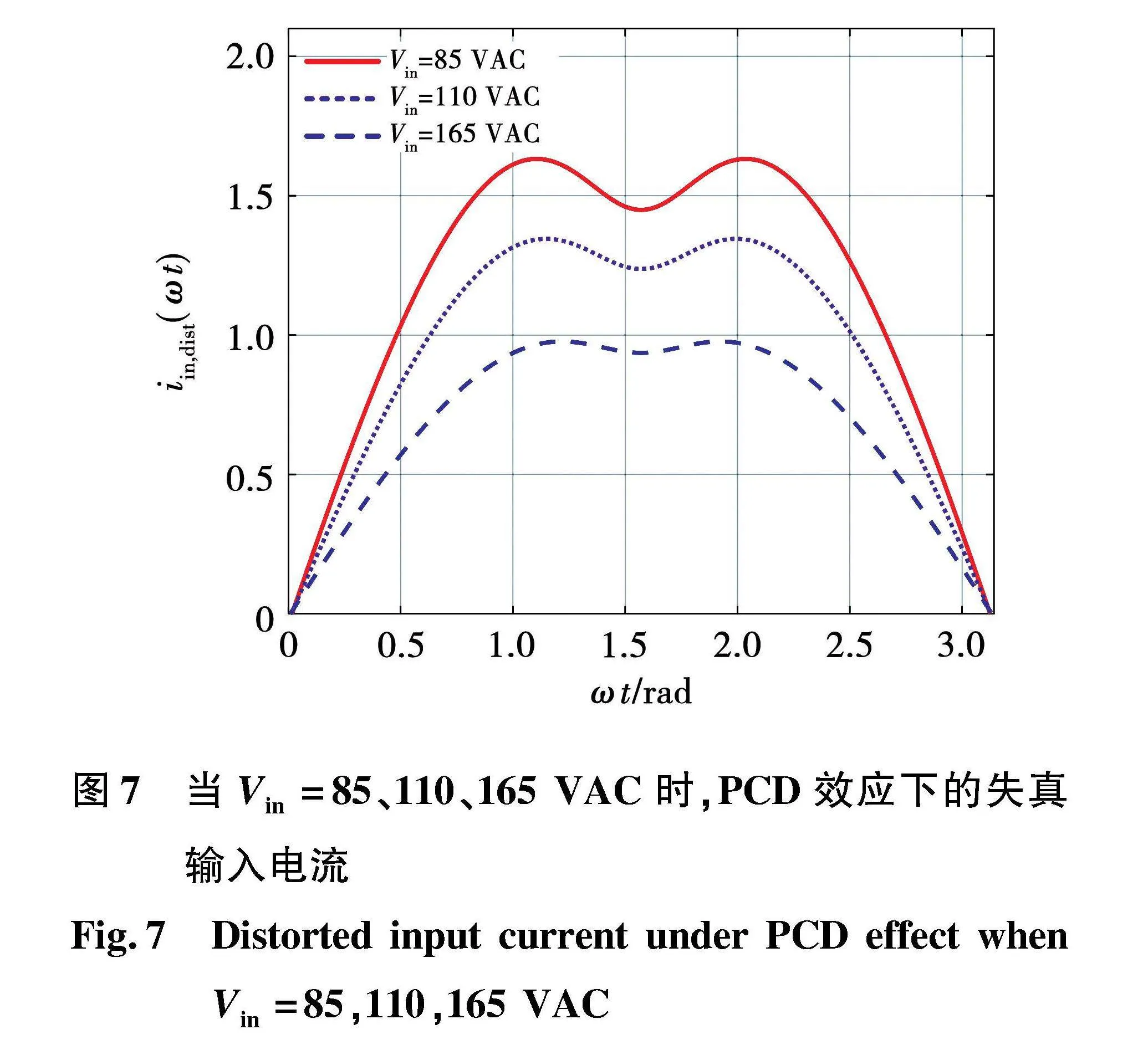
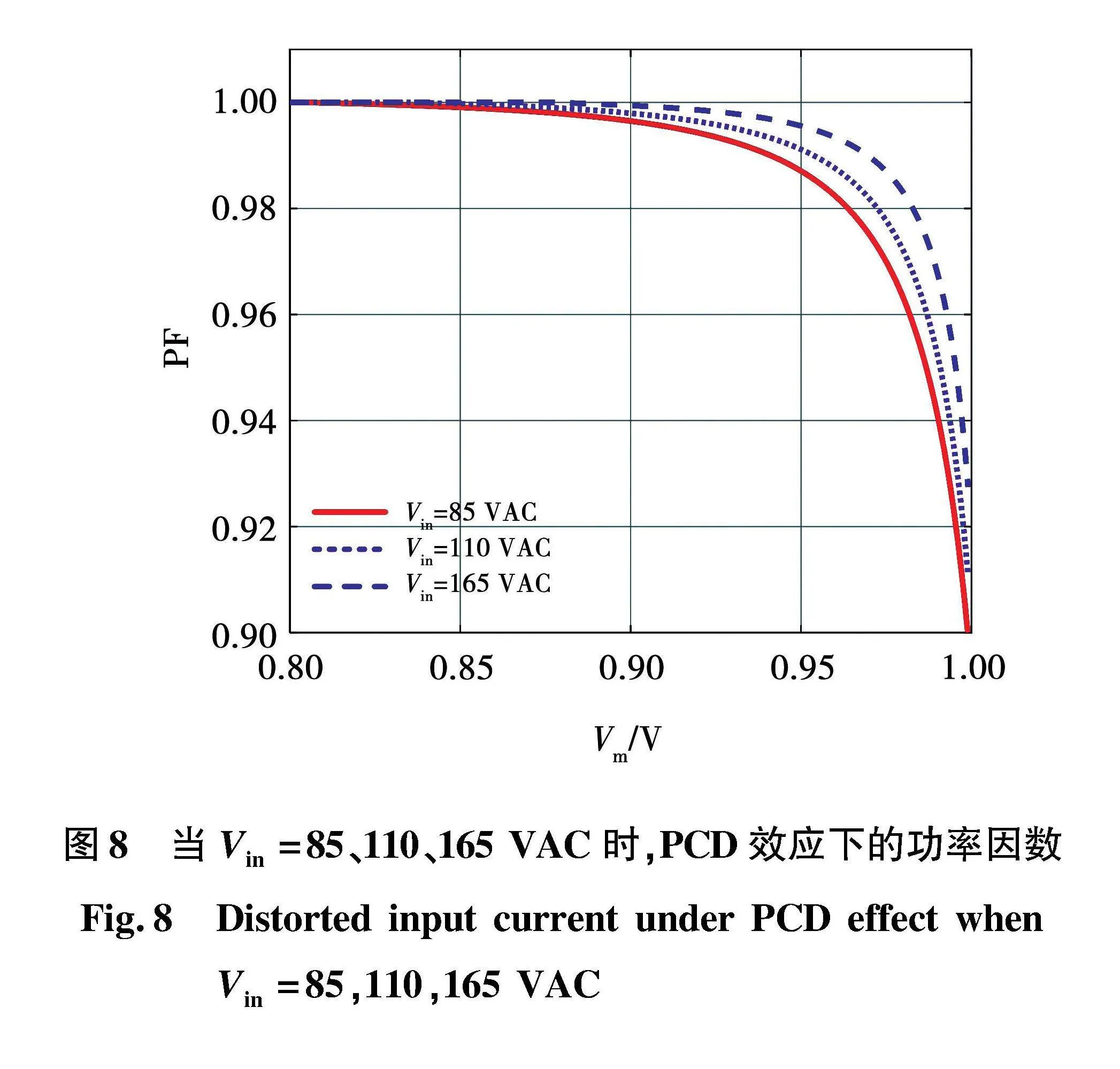
根据第1～2节的分析可知，各类寄生电阻会导致输入电流的失真，从而降低SACM控制下的功率因数。当不考虑寄生电阻时，SACM控制下的PF等于单位1，输入电流是标准正弦波形。若考虑寄生电阻，则输入电流会失真。式（15）给出失真输入电流的表达式，其仿真结果如图7所示。显然，输入电流波形在不同输入电压的情况下都呈现凹形。这表明降低了功率因数PF。

此外，式（16）给出了考虑PCD效应情况下的PF，其值跟随输入、输出电压变化。当输入电压从85到165 VAC变化时。PF随Vm/vo的波动情况如图8所示。

3.2" 基于补偿增益的电流重整形策略

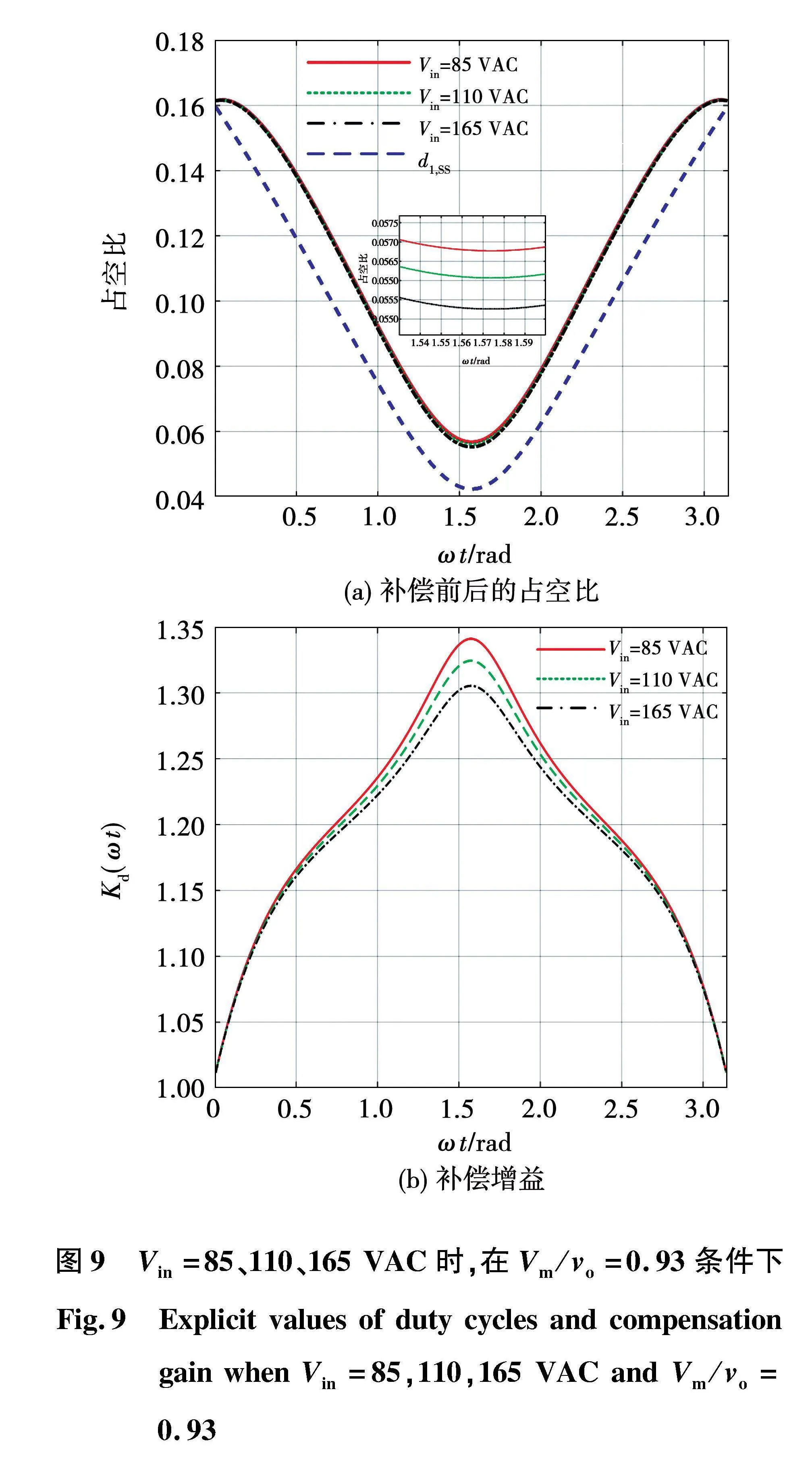
补偿增益Kd（ωt）具体体现在传统SACM控制器的输出上。在Vm/vo=0.93条件下，当Vin=85、110、165 VAC时的补偿前后的占空比及补偿增益如图9所示。

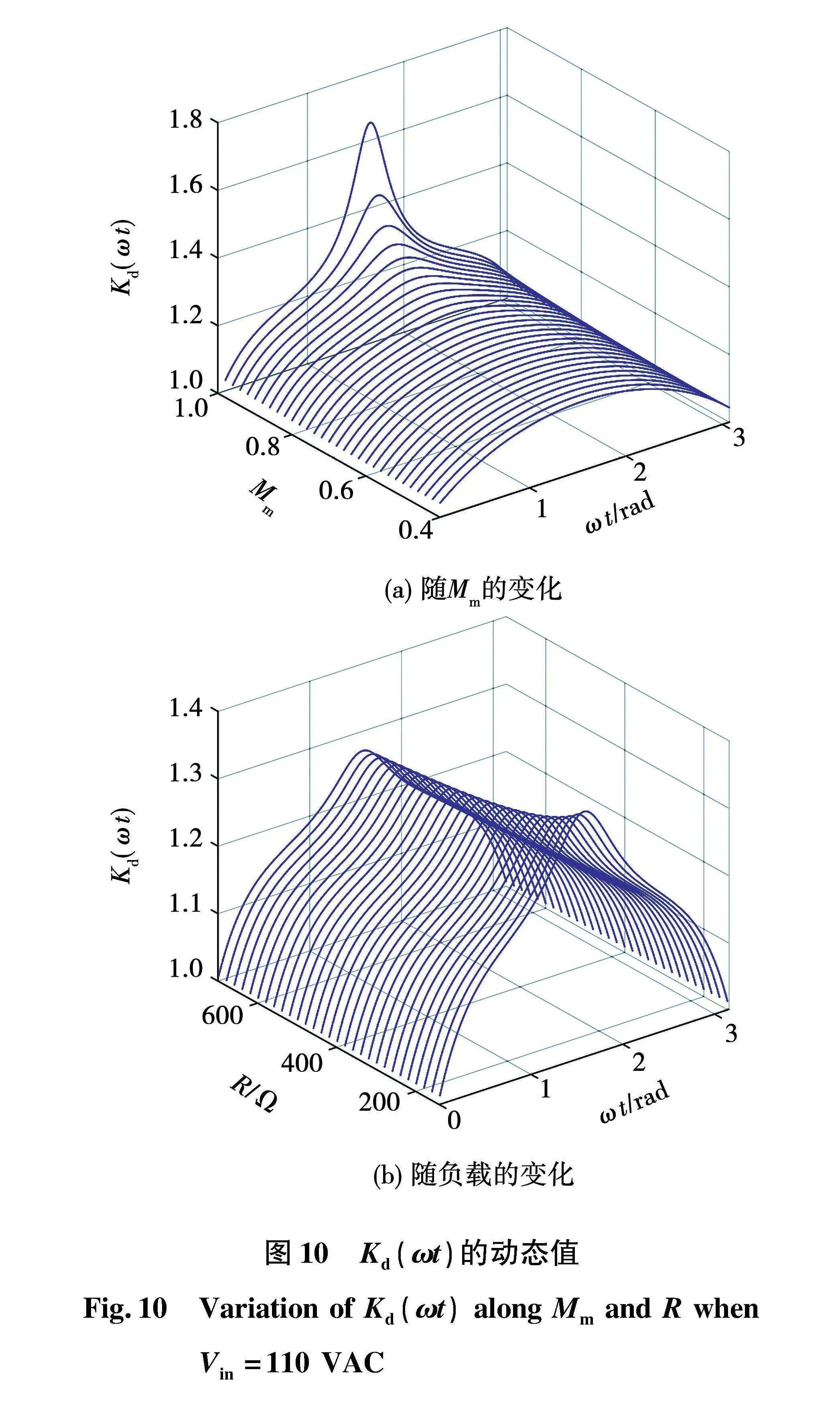
仿真结果表明：补偿后的占空比d1，res（ωt）通常比d1，SS（ωt）大。因此，可通过提高输入电流来消除PCD效应。此外，补偿增益随相位线性变化的波形呈现凸形。这说明当vm很高时，阻尼效应更加明显。

图10给出了补偿增益Kd（ωt）随Mm和R的变化趋势。显然，Kd（ωt）随Mm的增加，波形越来越凸。这是因为当Mm很大时，电流失真更加明显。此外，Kd（ωt）几乎不随负载电阻变化。因此，负载的变化对补偿策略的影响很小。

4" 实验

为了验证电流重整形策略的有效性，搭建了DCM升压型PFC变换器的样机如图11所示。

系统硬件包括一个控制模块和一个电源模块。控制模块是用Altera Cyclone IV FPGA来实现的，电源模块包括主功率级电路和信号采样电路。功率级设备的主要类型和重要参数如下：输入整流桥GBU6J;电源开关IPW65R150CFD;升压电感NPH107060（15.5 μH）;输出电容LGM2W471MELB40（470 μF）;整流二极管VS-6EVL06HM3;输入滤波电感230 μH;输入滤波电容470 nF。

通过两个单通道15位A/D转换芯片（ADS8318），实现了对线路电压与输出电压采样。同时也通过一种分辨率为1 V/A的电流探头放大器（TCP312 A）实现了将输入电流同步输出的功能。

接下来的实验均在SACM和电流重整形的控制条件下进行的，实现了对输入电流、PF和全谐波失真在不同条件下的测量。

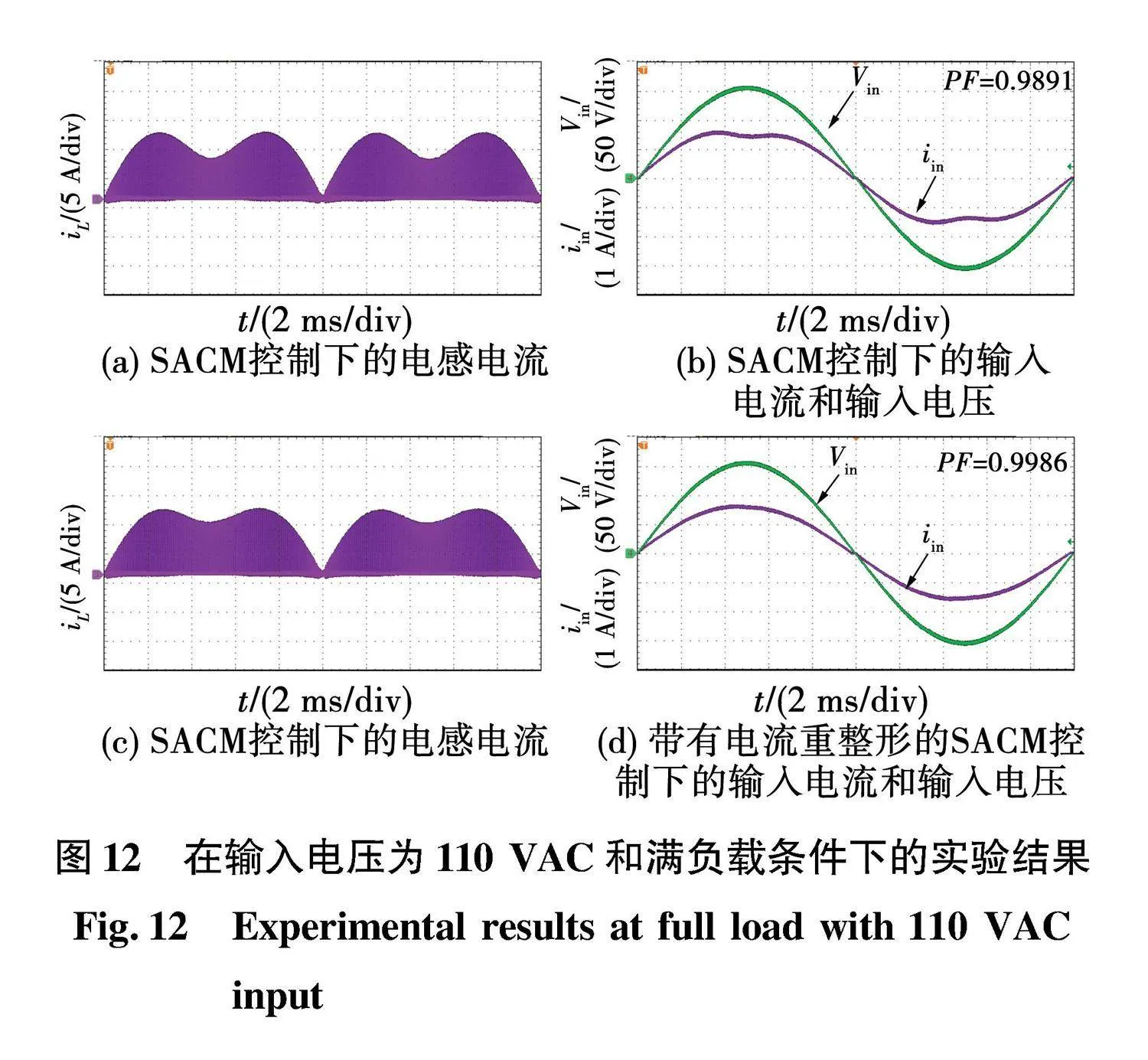
根据第3节的分析可知，由于寄生电阻的存在，电感电流具有阻尼特性，能导致输入电流失真，并降低功率因数PF。图12表示输入电流在输入电压110 VAC和满负载条件下的实验结果。

图12（a）和图12（b）表示了在传统SACM控制条件下的实验结果，其中Vm/vo设为0.93。输入电流的测量匹配于相应的仿真。相对于正弦波，输入电流的波形呈现凹形，而且PF值为0.989 1，为了减小输入电流的失真，电流重整形下的SACM控制通过采用Kd（ωt）补偿，增加了它的占空比，如图12（c）和图12（d）所示，这种控制策略将输入电流重整为正弦波。在输入电压为110 VAC时，功率因数提高到了0.998 6。

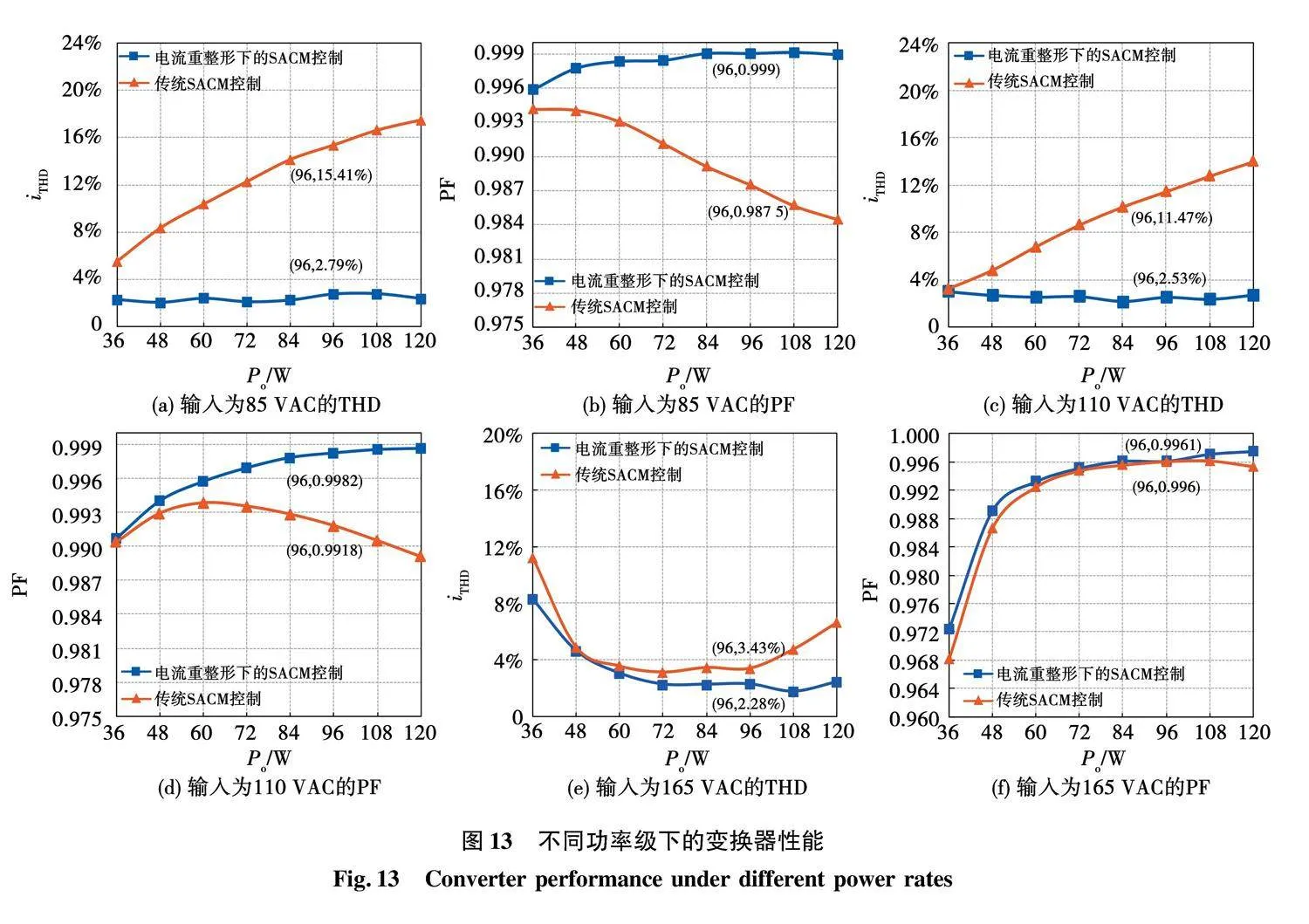
此外，图13给出了功率级在36～120 W的范围对变换器系统相关参数的测量。实验结果表明，与传统SACM控制相比，电流重整形策略能实现更高PF和更低THD。

5" 结" 论

本文重点研究了在考虑寄生电阻存在的情况下的PCD效应以及DCM升压型PFC变换器的PF。基于阻尼电感电流模型的分析，研究发现，PCD效应能导致很大的电流失真。降低了SACM控制下的PF。为了减少PCD效应，通过在不同条件下推导得到的补偿增益，能将输入电流重整为正弦波。并且通过实验证明了补偿增益几乎不随负载电阻变化。此外，这种电流重整形补偿方法能提高变换器在大功率范围内的PF。并通过仿真与实验。验证了这种控制方法的有效性。

参 考 文 献：

［1］" 姚嵩， 侯俊芳. 升压型PFC调制器的低谐波失真设计 ［J］. 电子器件， 2021， 44（6）： 1469.

YAO Song， HOU Junfang. Low harmonic distortion design of Boost PFC modulator［J］. Journal of Electronic Devices， 2021， 44（6）： 1469.

［2］" OKILLY A H， JEONG H， BAEK J. Optimal IP current controller design based on small signal stability for THD reduction of a high-power-density PFC boost converter［J］. Applied Sciences， 2021， 1（2）： 539.

［3］" 李刚， 邱伟， 李舒维. 基于反馈线性化的Boost PFC控制策略研究［J］. 现代电子技术， 2021， 44（15）： 115.

LI Gang， QIU Wei， LI Shuwei. Research on Boost PFC control strategy based on feedback linearization［J］. Modern Electronic Techniques， 2021， 44（15）： 115.

［4］" 曾燊杰， 李红梅， 张恒果， 等. Boost PFC变换器的无模型预测电流控制［J］. 电力自动化设备， 2020， 40（1）： 106.

ZENG Shenjie， LI Hongmei， ZHANG Hengguo， et al. Model-free predictive current control of Boost PFC converter［J］. Electric Power Automation Equipment， 2020， 40（1）： 106.

［5］" KIM J， CHOL H， WON C Y. New modulated carrier controlled PFC boost converter［J］. IEEE Transactions on Power Electronics， 2019， 33（6）： 1.

［6］" 林维明， 肖健， 张亮亮. 升压型Boost-PFC电路的频率反走临界电流控制［J］. 电机与控制学报， 2022， 26（4）： 66.

LIN Weiming， XIAO Jian， ZHANG Liangliang. Frequency backwalking critical current control of Boost-PFC circuit［J］. Electeric Machines and Control， 2022， 26（4）： 66.

［7］" KIM J，WON C Y. Improved modulated carrier controlled PFC boost converter using charge current sensing method ［J］. Energy Weekly News， 2018， 11（4）： 717.

［8］" 周国华， 田庆新， 冷敏瑞，等. 具有低输出电流纹波的高功率因数Cuk PFC变换器［J］. 电机与控制学报， 2019， 23（12）：32.

ZHOU Guohua， TIAN Qingxin， LENG Minrui， et al. Cuk PFC converter with high power factor with low output current ripple［J］. Electric Machines and Control， 2019， 23（12）：32.

［9］" ZHU Haoqi， LIU Dongliang， ZHANG Xu， et al. Reliability of boost PFC converters with improved EMI filters［J］. Electronics， 2018， 7（12）： 413.

［10］" 刘斌， 李伦全， 叶昌， 等. 一种新型高效的多功能Buck/Boost/Buckboost型功率因数校正电路［J］. 电网技术， 2021， 45（3）： 1142.

LIU Bin， LI Lunquan， YE Chang， et al. A new high-efficiency multi-function Buck/Boost/Buckboost power factor correction circuit［J］. Power System Technology， 2021， 45（3）： 1142.

［11］" 杨平， 范文， 胡富平， 等. 三态Boost PFC变换器的高功率因数和轻载效率提升方法研究［J/OL］. 中国电机工程学报： 1-12［2022-10-18］. http：//kns.cnki.net/kcms/detail/11.2107.tm.20220307.1749.010.html．

YANG Ping， FAN Wen， HU Fuping， et al. Study on high power factor and light load efficiency improvement method of three-state Boost PFC converter［J/OL］. Proceedings of the CSEE：1-12［2022-10-18］. http：//kns.cnki.net/kcms/detail/11.2107.tm.20220307.1749.010.html．

［12］" 曾燊杰， 李红梅， 张恒果， 等. Boost PFC变换器的无模型预测电流控制［J］. 电力自动化设备， 2020， 40（1）： 106.

ZENG Shenjie， LI Hongmei， ZHANG Hengguo， et al. Model-free predictive current control of Boost PFC converter［J］. Electric Power Automation Equipment， 2020， 40（1）： 106.

［13］" 罗欢， 许建平， 罗艺文， 等. 全输入电压范围高功率因数脉冲序列控制DCM Boost PFC变换器［J］. 中国电机工程学报， 2019， 39（6）： 1758.

LUO Huan， XU Jianping， LUO Yiwen， et al. Full input voltage range high power factor pulse train control DCM Boost PFC converter［J］. Proceedings of the CSEE， 2019， 39（6）： 1758.

［14］" 赵晨光， 冯全源， 王丹. 一种DCM峰值电流控制模式AC/DC反激转换器环路的设计［J］.微电子学，2015，45（3）：345.

ZHAO Chenguang， FENG Quanyuan， WANG Dan. Design of a DCM peak current control mode AC/DC flyback converter loop［J］. Microelectronics， 2015， 45（3）： 345.

［15］" GENC N， UZMUS H. Digital control of bridgeless interleaved PFC boost converter based on predicted input current ［J］. IETE Journal of Research， 2019， 68（3）：1914.

（编辑：刘素菊）