基于分形原理的球形静电纺丝头建模及其电场仿真

摘 " "要： 为了提高球形纺丝头表面场强，精确控制射流的发射位点，基于分数维原理发明了一种球分形静电纺丝头，其结构通过在大球表面多次阵列一定数量小球获得，极大提高了小球表面的电荷密度，增大电场强度，在可控发射纺丝流体的同时有效降低纺丝电压，既节省能源又提高纺丝过程安全性。利用有限元软件COMSOL对球分形纺丝头进行了场强数值模拟分析，研究了小球数量（排列方式）和结构尺寸对电场强度及分布的影响，确定了小球数量和半径。结果表明：当大球半径为60 mm、小球半径为2.0 mm时，大球表面可等间距排列49个小球，该球分形纺丝头的场强比球状纺丝头提高了4倍，可在49个小球表面发射至少49个射流，小球间场强干扰低，射流位置固定，可增加电纺膜的均匀性。

关键词： 静电纺丝；球分形结构；电场分布；有限元分析

中图分类号： TS103.7；TQ340.5 " " " " " " 文献标志码： A " " " " " " " "文章编号： "１６７１－０２４Ｘ（２０24）０2－００43－06

Design of spherical spinneret based on fractal principle and its electric field simulation

LIU Yanbo1，2， HU Kai1， HAO Ming1，2， HU Xiaodong1，2， YANG Bo1

（1. School of Textile Science and Engineering， Wuhan Textile University， Wuhan 430200， China； 2. School of Textile Science and Engineering， Tiangong University， Tianjin 300387， China）

Abstract： In order to improve the surface field intensity of the spherical spinneret and precisely control the jet emission， a spherical fractal electrostatic spinneret was invented based on the fractal dimension principle， whose structure is obtained by repeatedly arraying a certain number of small balls on the surface of a large ball， and the charge density on the surface of the small balls is greatly increased， and the electric field intensity is increased， which effectively reduces the spinning voltage while controlling the emission of the spinning fluid， saving energy and improving the safety of the spinning process. A numerical simulation of the field intensity of the spherical fractal spinneret was carried out using the finite element software COMSOL to study the effect of the number （arrangement） ， size and structure of spheres on the electric field intensity and distribution， and to determine the number and radius of the spheres. The results show that when the large sphere radius is 60 mm and the small sphere radius is 2.0 mm， the surface of the large sphere can be equally spaced 49 small spheres， the field intensity of this spherical fractal spinneret is 4 times higher than that of the spherical spinneret， and at least 49 jets can be emitted on the surface of the 49 small spheres， with low field interference between the small spheres and fixed jet position， which can increase the uniformity of the electrospun film.

Key words： electrospinning； spherical fractal structure； electric field distribution； finite element analysis

静电纺丝制备的纳米纤维所表现的独特性能使其在过滤[1-3]、传感器[4-6]、组织工程[7]、生物医学[8]等领域有着广泛的应用。对于针头式静电纺丝装置，近年来，研究人员开发了多种多针头[9-10]和无针[11-16] 静电纺丝设备来提高纤维产量。对于多针头静电纺，针头间的电场干扰会使射流发生偏离[17-18]，通过改变多针头的结构和排列 [19-20]可以减少场强干扰，但针头易堵也会影响纤维的产量和纺丝过程的稳定性。

无针静电纺丝技术大幅度提高了生产效率，无针头堵塞问题，且易清理。捷克Elmarco公司[21]开发出转辊式无针头静电纺丝头（纳米蜘蛛一代），然后又开发了金属线形纺丝头（纳米蜘蛛二代），大幅度降低了纺丝电压。Niu等[22]研究表明，在螺旋线喷丝板上加装二次线圈增强了纤维发生区的电场，降低了射流起始电压，大大提高了静电纺丝性能。Yang等 [23-24]研究表明，基于Von Koch曲线设计的分形无针纺丝头，能够增加射流发射点、场强更大更均匀。熊健[25]研究表明，球形纺丝头具有表面电场均匀且集中、自由液面电荷分布均匀且密度高等特点，可以在整个球形曲率液面上激发多射流，提升射流数量。但普通球形纺丝头需要较高的纺丝电压，开放式供液使溶剂易挥发，未完全纺丝的溶液沉积在纺丝头表面，使纺丝头场强分布不均匀，影响纺丝过程的稳定性。

自相似原则和迭代生成原则是分形理论[26]最重要的原则，自相似和迭代生成使分形的形态具有标度不变性，可无限生成更精细的结构。为了能够连续稳定地制备纳米纤维，受球形静电纺丝装置和分形原理的启发，本课题组发明了一种球分形纺丝头。利用分形原理的自相似原则在大球表面阵列多个小球得到球分形结构纺丝头。使用COMSOL软件研究了纺丝头的结构参数包括小球的半径、阵列个数对电场分布的影响，选择合适的小球半径和阵列数量，得到场强高且均匀的工作电场，以期为无针静电纺丝制备纳米纤维提供理论基础，同时实现降低能耗、节约能源的目的。

1 电场模拟与装置设计

1.1 COMSOL模拟原理及参数

COMSOL 作为一款以有限元分析为基础的模拟仿真软件，通过以下流程进行模拟分析，即确定模拟内容→建立模型→设定求解域和边界条件→进行网格划分→求解器求解→对模拟结果进行后处理。使用 AC/DC模块中的静电物理场对静电场进行模拟，其中静电场强遵循泊松方程[20]

式中：ε0为真空相对介电常数；εγ为介质相对介电常数；V为电势能；ρ为空间电荷密度。根据相关的等式 E = -V可得到对应的场强值。

1.2 模型建立与纺丝头结构

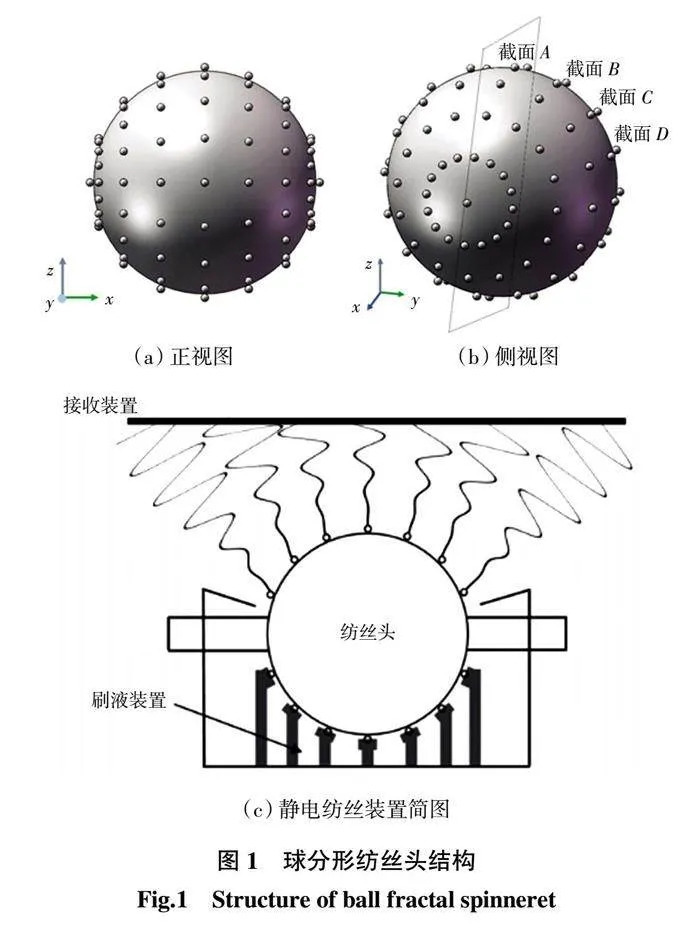
图1 所示为球分形纺丝头机构。首先采用圆周阵列的方法使小球均匀地分布在大球正面圆周上，单次阵列个数为n，每个小球的间距相等；再以该圆周上的小球为阵列实体沿大球侧面进行相同数量的圆周阵列，使小球均匀地分布在大球表面，大球半径为60 mm，小球半径r为1.5～3.0 mm。以r = 2.0 mm小球单次阵列数量n=16为例，球分形纺丝头正视图如图1（a）所示，侧视图如1（b）所示，令xz（y = 0）截面为截面A，纺丝头的结构关于截面A对称，截面B与截面A的夹角度数为2π/n，从侧视图可以看出各截面上的小球都呈圆周分布，除了旋转轴上的小球外，都能供液进行纺丝。球分形静电纺丝装置如图1（c）所示，纺丝头通过旋转带液进行纺丝。

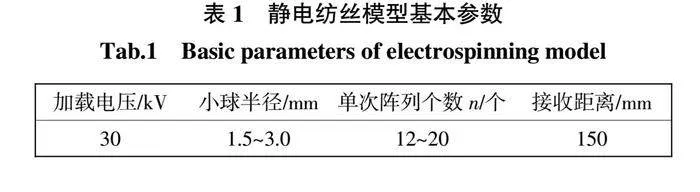
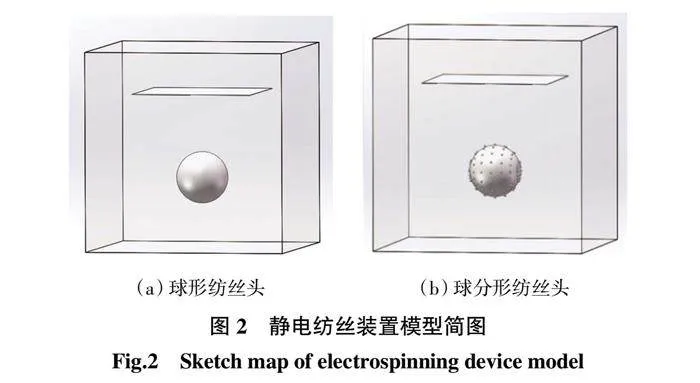
为简化计算，模型只含球形/球分形纺丝头、接收板和空气。静电纺丝装置模型简图如图2所示，图2（a）为半径64 mm的球形纺丝头装置模型，图2（b）为大球半径为60 mm、小球半径r = 2.0 mm的球分形纺丝装置模型。正方形空气域边长为500 mm，矩形收集薄板尺寸为300 mm × 300 mm × 1 mm。为了使模拟结果能够有效的反映实际状况，需要对模型中涉及的关键参数进行设置：空气的相对介电常数为1.0，纺丝头和接收板材料属性为金属钢，其相对介电常数为1.5。模拟过程中，空气场的边界设定为零电荷，以实现有限范围内静电纺丝周围环境为无限远，模拟结果为纺丝头表面附近电场的场强。其他模型参数如表1所示。

2 电场仿真结果分析

2.1 小球对纺丝头电场的影响

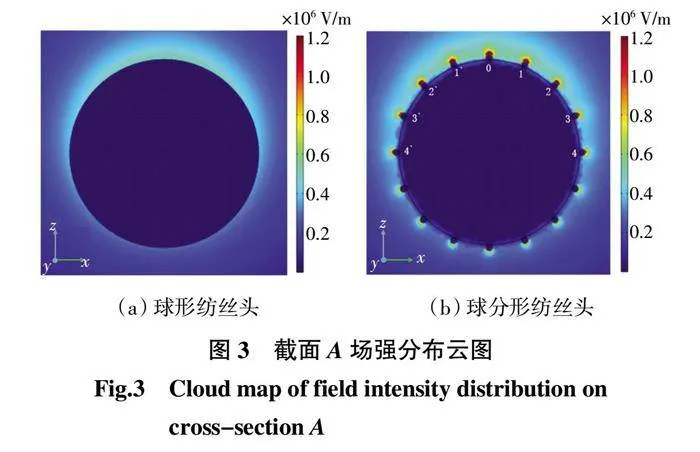
为探究小球对纺丝头电场的影响，对球形和球分形纺丝头进行仿真，纺丝头截面A场强分布如图3所示。

由图3可以看出，纺丝模型中各部分颜色呈一定规律分布，从纺丝头表面向外逐渐由红色变为蓝色，根据颜色图例表示的含义，颜色越靠近红色场强越高，可以看出球分形纺丝头表面的小球场强更高，静电纺丝过程中射流更容易在这些区域形成。纺丝头上表面距离接收板更近，场强更高，对球分形纺丝头上各截面上的小球进行编号，后续电场模拟结果皆为A-D截面（截面数量由n决定）x轴上方各小球的场强峰值。2种纺丝头截面A场强分布如图4所示。

由图4可以看出，球形纺丝头截面A场强大小呈曲线分布，尽管三维球面不同位置到达接收装置距离不同，其场强值稳定分布在0.37 × 105 ～ 0.52 × 105 V/m之间，在纺丝头截面A上场强分布均匀。r = 2.0 mm时球分形纺丝头截面A上场强分布在1.44 × 106 ～ 2.03 × 106 V/m之间，场强远高于球形纺丝头表面的场强，这是因为纺丝头表面的小球有更高的曲率，表面电荷更加密集，电场强度更高。对2种纺丝头表面相同位点的场强进行计算，可知：球形纺丝头表面场强均值为0.44 × 105 V/m，场强CV值为10.55%；球分形纺丝头场强均值为1.71 × 105 V/m，场强CV值为10.10%，场强提升了4倍，场强CV值降低了0.45%。这是由于球形纺丝头表面光滑无尖端电场干扰，场强不均率由表面各位点与接收装置距离不同所导致；而球分形纺丝头具有多个高场强区域，能在改善电场的同时仍然保持与球形纺丝一样略窄的场强分布，说明该结构的纺丝头表面各小球间电场干扰极小，有利于纺丝过程的稳定。

2.2 小球半径对纺丝头场强的影响

对不同r值的球分形纺丝头进行仿真，分析小球半径对场强的影响，小球半径取值1.5～3.0 mm，步长为0.5 mm，纺丝头表面场强分布云图如图5所示。

由图5中场强云图颜色变化可以看出，随着r的增大，大球表面的颜色逐渐趋近于蓝色，说明大球场强降低，表面电荷向小球迁移的数量变多，高场强区域更多地集中在小球表面。与此同时，增大r会导致表面各小球红色区域逐渐分散，表面电荷密度下降，场强降低。所以，适当地增大小球的半径，有助于电荷向小球表面迁移，形成更大的高场强区域，提高电能利用率。不同r的球分形纺丝头的各截面上小球场强分布如图6所示。

由图6可知，纺丝头表面小球的场强随着半径的增大逐渐降低。r = 1.5 mm时，各截面小球场强在1.54×106 ～ 2.1×106 V/m之间；r = 3.0 mm时，各截面小球场强在1.28×106 ～ 1.93×106 V/m之间，这主要是由于小球半径的增大使得单个小球表面电荷密度和场强降低所导致的。随着各截面与截面A夹角度数的增加，0-3号小球的场强分布变窄。以r = 3.0 mm时的纺丝头为例，截面A上0到3号小球间场强差值最大为0.55×106 V/m，截面D上0到3号小球间场强差值最大为0.30×106 V/m，场强分布变窄，这是因为截面上各小球接收距离的差异变小所导致的。当与截面A垂直时（夹角为90°），各小球与接收板的距离相等，场强最低且趋于相等。各截面间场强的分布范围将会影响纺丝头的整体场强均匀性，不同r值纺丝头各截面上的小球场强均值与纺丝头的整体场强分布如图7所示。

由图7可知，r相同时从截面A到截面D上小球的场强均值逐渐变小；随着r增大，纺丝头的整体场强（7个截面上的49个小球）CV值逐渐变大。这主要是由于随着球分形纺丝头的半径增大，各截面上小球与接收板的距离差异和电场干扰变大，小球场强分布变宽所导致的。r = 1.5 mm时，场强CV值为9.80%；当r增大到2.0 mm，小球表面高场强区域增大，而场强CV值仅增大0.3%；进一步增大r，小球表面电荷密度下降，场强CV值明显增大，不利于高场强区域的集中和均匀分布。所以，本文选择小球半径为2.0 mm的纺丝头进行下一步研究。

2.3 小球数量对球分形纺丝头场强的影响

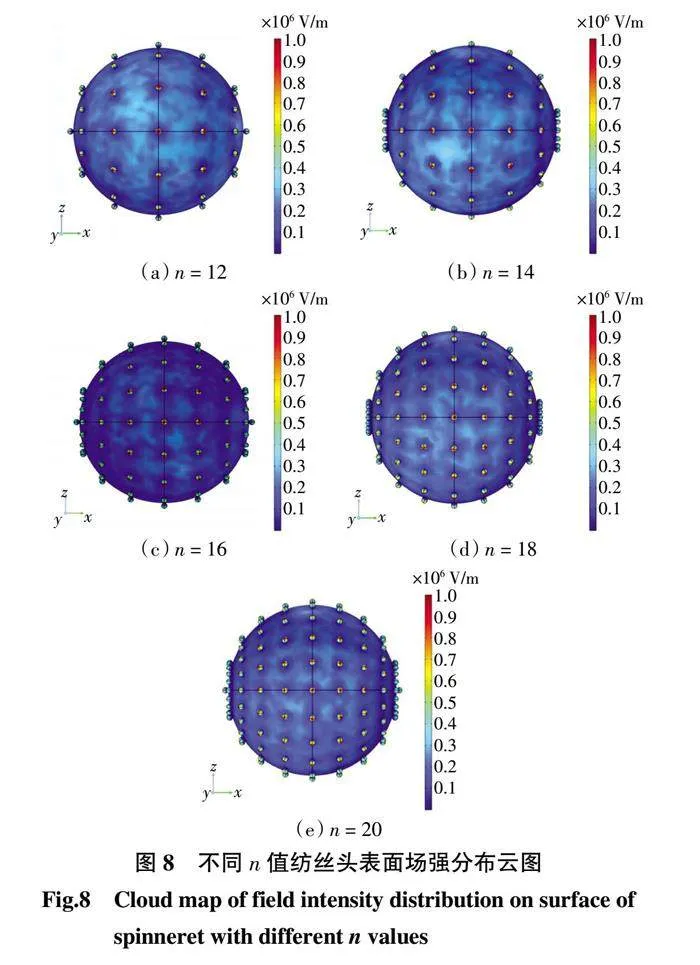
为探究小球数量对电场的影响，对不同n值的球分形纺丝头进行模拟，n取值范围为12～20，步长为2 mm，纺丝头表面场强分布如图8所示。

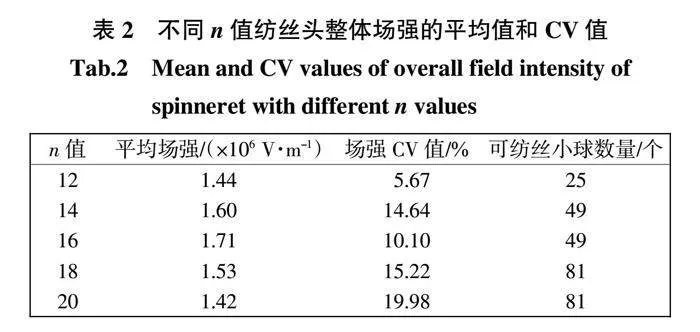
由图8可以看出，随着n值的增大，纺丝头表面小球的数量变多，小球间的距离变小，大球表面电荷向小球迁移的数量变多，场强颜色越趋近于蓝色，这有利于在小球表面形成更多高场强区域激发更多的射流。不同n值的纺丝头场强分布如表2所示。

由表2可知，随着n值增大，纺丝头的整体场强平均值呈现出先增大后减小的趋势。小球数量越多，有利于电荷向小球表面迁移，增加可纺丝区域，但是小球数量过多会导致小球表面电荷密度下降，同时过小的球间距会产生电场干扰。n = 12时，最多有25个小球进行纺丝，虽然该结构纺丝头小球间距离最远，无电场干扰，场强CV值为5.67%，但是可纺丝小球的数量太少，不利于提高纺丝效率。当n = 14、18时，纺丝头左右两端的小球距离接受板较远，各截面上的小球与接收板的距离差异较大，影响了纺丝头整体场强的均匀性。n值增大到20时，该结构纺丝头的整体平均场强降低至1.42 × 106 V/m，场强CV值增大到19.98%。这主要是由于小球间的距离以及表面电荷密度减小，各截面上的小球与接收板的距离差异增大，截面间场强差异增大所导致的。当n = 16时，通过对比球形纺丝头相同位点的场强分布可知，该结构的纺丝头小球间无电场干扰，纺丝头的平均场强达到最大为1.71 × 106 V/m，场强CV值为10.10%，可纺丝小球数量多，有利于纳米纤维的制备。

3 结 论

本文以球形纺丝头为研究对象，设计了不同结构的球分形纺丝头，保持大球半径不变，改变表面小球的半径和阵列数量，研究了场强分布规律，得出以下结论：

（1） 相比于普通的球形纺丝头，球分形纺丝头的纺丝位点位于小球表面，纺丝位点相互独立，互不干扰。

（2） 球分形纺丝头表面小球具有较高的曲率，场强为球形纺丝头的4倍，场强有了极大的提高，可降低纺丝过程中的施加电压，节省能源。

（3） 小球数量一定时，适当增大小球半径有利于电荷向小球表面迁移，可提高电能利用率。半径过大，各截面上小球与接收板的距离差异和电场干扰变大，影响场强均匀性。当小球半径为2.0 mm时，纺丝头场强最高且分布较窄，所以小球的最佳半径为2.0 mm。

（4） 增加小球的数量，可增加纺丝位点，提高产量。但是数量过多，会降低纺丝头表面场强，同时过小的球间距会产生电场干扰。纺丝小球单次阵列的数量为16时，场强均值最高且分布较窄，表面49个小球最低可产生49个射流进行纺丝，有利于提高产量。

参考文献：

[1] " "SUNDARRAJAN S， TAN K L， LIM S H， et al. Electrospun nanofibers for air filtration applications[J]. Procedia Engineering， 2014， 75： 159-163.

[2] " "BAHK Y K， WANG J. Filtration and length determination of airborne carbon nanotubes in the submicrometer range using nanofiber filters[J]. Aerosol and Air Quality Research， 2014， 14（5）： 1352-1359.

[3] " "姚金波，刘 垚，田文军，等. 静电驻极PVDF-TiO2 /Si3N4纳米纤维膜的制备及其空气过滤性能[J]. 天津工业大学学报， 2022， 41（2）： 20-24，48.

YAO J B， LIU Y， TIAN W J， et al. Preparation of electrostatic charging PVDF-TiO2 /Si3N4 nanofiber membrane and its air fil-tration performance[J]. Journal of Tiangong University， 2022， 41（2）： 20-24，48（in Chinese）.

[4] " "GUAN X Y， XU B G， GONG J L. Hierarchically architected polydopamine modified BaTiO3@P（VDF-TrFE） nanocomposite fiber mats for flexible piezoelectric nanogenerators and self-powered sensors[J]. Nano Energy， 2020， 70： 104516.

[5] " "WU S D， DONG P H， CUI X， et al. The strategy of circuit design for high performance nanogenerator based self-powered heart rate monitor system[J]. Nano Energy， 2022， 96： 107136.

[6] " "CHEN Y X， DENG Z R， OUYANG R， et al. 3D printed stre-tchable smart fibers and textiles for self-powered e-skin[J]. Nano Energy， 2021， 84： 105866.

[7] " "CHEN M X， GAO S A， WANG P， et al. The application of electrospinning used in meniscus tissue engineering[J]. Journal of Biomaterials Science， Polymer Edition， 2018， 29（5）： 461-475.

[8] " "AL-ENIZI A， ZAGHO M， ELZATAHRY A. Polymer-based electrospun nanofibers for biomedical applications[J]. Nanomaterials， 2018， 8（4）： 259.

[9] " "SALEHHUDIN H S， MOHAMAD E N， MAHADI W N L， et al. Simulation and experimental study of parameters in multiple-nozzle electrospinning： Effects of nozzle arrangement on jet paths and fiber formation[J]. Journal of Manufacturing Processes， 2021， 62： 440-449.

[10] "YANG Y， JIA Z D， LI Q， et al. A shield ring enhanced equilateral hexagon distributed multi-needle electrospinning spinneret[J]. IEEE Transactions on Dielectrics and Electrical Insulation， 2010， 17（5）： 1592-1601.

[11] "HOLOPAINEN J， PENTTINEN T， SANTALA E， et al. Needleless electrospinning with twisted wire spinneret[J]. Nanotechnology， 2015， 26（2）： 025301.

[12] "MOLNAR K， NAGY Z K. Corona-electrospinning： Needleless method for high-throughput continuous nanofiber production[J]. European Polymer Journal， 2016， 74： 279-286.

[13] "LIU Z， ANG K K J， HE J H. Needle-disk electrospinning inspired by natural point discharge[J]. Journal of Materials Science， 2017， 52（4）： 1823-1830.

[14] "ALI U， NIU H T， KHURSHID M F， et al. Electrospinning behavior of needleless spinneret with a popular mace shape[J]. The Journal of the Textile Institute， 2019， 110（3）： 349-357.

[15] "ALI U， ABBASS A， KHURSHID F， et al. Needleless electrospinning using a flat wheel spinneret[J]. Journal of Engineered Fibers and Fabrics， 2017， 12（3）： 155892501701200.

[16] "AHMAD A， ALI U， NAZIR A， et al. Toothed wheel needleless electrospinning： A versatile way to fabricate uniform and finer nanomembrane[J]. Journal of Materials Science， 2019， 54（21）： 13834-13847.

[17] "THERON S A， YARIN A L， ZUSSMAN E， et al. Multiple jets in electrospinning： Experiment and modeling[J]. Polymer， 2005， 46（9）： 2889-2899.

[18] "VARESANO A， CARLETTO R A， MAZZUCHETTI G. Experimental investigations on the multi-jet electrospinning proc-ess[J]. Journal of Materials Processing Technology， 2009， 209（11）： 5178-5185.

[19] "YANG Y， JIA Z D， LI Q， et al. Multiple jets in electrospinning[C]//2006 IEEE 8th International Conference on Properties amp; applications of Dielectric Materials. Bali， Indonesia：IEEE， 2007： 940-943.

[20] "刘延波， 曹红， 张立改， 等. 多针头静电纺丝过程中场强的改善[J]. 成都纺织高等专科学校学报， 2017， 34（2）： 30-36.

LIU Y B， CAO H， ZHANG L G， et al. Improvement of field strength in multi-needle electrostatic spinning process[J]. Journal of Chengdu Textile College， 2017， 34（2）： 30-36（in Chinese）.

[21] "张艳萍， 张莉彦， 马小路， 等. 无针静电纺丝技术工业化进展[J]. 塑料， 2017， 46（2）： 1-4， 12.

ZHANG Y P， ZHANG L Y， MA X L， et al. Recent development of industrialized needleless electrospinning technology[J]. Plastics， 2017， 46（2）： 1-4， 12（in Chinese）.

[22] "NIU H T， ZHOU H A， YAN G L， et al. Enhancement of coil electrospinning using two-level coil structure[J]. Industrial amp; Engineering Chemistry Research，2018：57（45）：15473-15478.

[23] "YANG W X， LIU Y B， ZHANG L G， et al. Optimal spinneret layout in Von Koch curves of fractal theory based needleless electrospinning process[J]. AIP Advances，2016，6（6）： 065223.

[24] "杨文秀. 基于分形原理的静电纺丝技术研究和锂电池隔膜研发[D]. 天津： 天津工业大学， 2016.

YANG W X. Research on electrostatic spinning technology based on fractal principle and development of lithium battery separator[D]. Tianjin： Tianjin Polytechnic University， 2016（in Chinese）.

[25] "熊健. 曲率液面静电纺丝机理及在净化领域的应用[D]. 上海： 东华大学， 2022.

XIONG J. Curvature-surface electrospinning and its applications in purification[D]. Shanghai： Donghua University， 2022 （in Chinese）.

[26] "MANDELBROT B B. Stochastic models for the Earth′s relief， the shape and the fractal dimension of the coastlines， and the number-area rule for islands[J]. Proceedings of the National Academy of Sciences of the United States of America， 1975， 72（10）： 3825-3828.

本文引文格式：

刘延波， 胡楷， 郝铭， 等. 基于分形原理的球形静电纺丝头建模及其电场仿真[J]. 天津工业大学学报，2024， 43（2）： 43-48.

LIU Y B， HU K， HAO M， et al. Design of spherical spinneret based on fractal principle and its electric field simulation[J]. Journal of Tiangong University， 2024， 43（2）： 43-48（in Chi-nese）.