基于优化动力学模型的路径跟踪控制研究

何智成 王煜凡 韦宝侣 李智 卜腾辰

摘要：

针对一般路径跟踪模型预测控制器在高速大曲率工况下适应性差的问题，提出了一种基于优化动力学模型的自适应预测时域控制策略。首先，为解决经典动力学模型在较高侧向加速度工况下精度不足的问题，建立了包含侧倾转向和变形转向特性的优化模型，实现了车辆状态的较高精度预测；其次，为解决高速大曲率工况下固定预测时域控制效果不佳的问题，提出了基于二维高斯函数的自适应预测时域策略，以低算法复杂度实现了预瞄距离的实时调整；最后，通过CarSim/Simulink联合仿真实验验证了控制器在双移线道路上的控制效果，结果表明，横向位置峰值误差降低45.1%，横摆角峰值误差降低72.4%，设计的控制器对极限工况有更好的适应性。

关键词：智能网联汽车；横向动力学优化；路径跟踪；模型预测控制；自适应预测时域

中图分类号：U467

DOI：10.3969/j.issn.1004132X.2024.06.006

开放科学（资源服务）标识码（OSID）：

Research on Path Tracking Control Based on Optimized Dynamics Model

HE Zhicheng1  WANG Yufan1  WEI Baolv1，2  LI Zhi1  BU Tengchen1

1.State Key Laboratory of Advanced Design and Manufacturing Technology for Vehicle，

Hunan University，Changsha，410082

2.SAIC GM Wuling Automobile Co.，Ltd.，Liuzhou，Guangxi，545007

Abstract： In response to the poor adaptability of conventional path tracking model predictive controllers under high-speed and large-curvature conditions， an adaptive prediction horizon control strategy was proposed based on optimized dynamic models. Firstly， to address the issues of insufficient accuracy of classical dynamics models under high lateral acceleration conditions， an optimized model including roll steer and compliance steer was established， achieving higher precision prediction of vehicle states. Secondly， to address the issues of fixed prediction horizon control under high-speed and large-curvature conditions， an adaptive prediction horizon strategy was proposed based on two-dimensional Gaussian function， achieving real-time adjustment of preview distances with low algorithm complexity. Finally， the effectiveness of the controller on double-lane-change roads was verified throught CarSim/Simulink joint simulation. Results show that a reduction of 45.1% in lateral position peak errors and 72.4% in yaw angle peak errors indicate better adaptability of the designed controller to extreme conditions.

Key words： intelligent connected vehicle； lateral dynamics optimization； path tracking； model predictive control； adaptive prediction horizon

收稿日期：20231002

基金项目：湖南省杰出青年基金（2021JJ10016）；广西科技重大专项（2021AA04004）；柳州市科技计划（2022AAA0101）

0  引言

随着移动互联网、大数据和云计算等新一代信息技术的革命性突破，智能交通系统蓬勃发展［1］，其中自动驾驶技术是其关键推动力之一［2］。车辆在高速大曲率工况下产生较大的侧向加速度容易发生侧滑失稳现象，威胁驾乘人员的安全［3］，因此，智能汽车在此类工况下实现稳定准确的路径跟踪是自动驾驶运动控制的重要挑战。

国内外学者在路径跟踪控制研究中采用了多种控制算法，包括PID控制［4-5］、滑模控制［6-7］、鲁棒控制［8］、模型预测控制（model predictive control， MPC）［9］和模糊控制［10］等。近年来，由于MPC算法能够系统地处理车辆动力学约束，逐渐成为了研究热点。然而，在高速大曲率工况下，固定预测时域可能会影响路径跟踪的精度和车辆稳定性［11］，为此，一些学者提出了一系列改进措施。LIU等［12］提出了一种变步长的模型离散化方法，该方法在满足计算实时性的同时拥有更长的预测时域。白国星等［13］基于非线性模型预测控制算法，将预测时域同车辆速度和稳态转向角结合起来以设计控制器。CHEN等［14］提出了一种基于路径的自适应预测时域路径跟踪转向控制器。预测时域的变化策略应综合考虑车辆状态和道路信息，而且要以较低的算法复杂度满足实时性要求。

基于优化动力学模型的路径跟踪控制研究——何智成  王煜凡  韦宝侣等

中国机械工程 第35卷 第6期 2024年6月

另外，针对侧向加速度较大时经典动力学模型［15］精度不足的问题，刘文营等［16］根据纵向车速、等效侧偏刚度的变化规律，对线性二自由度模型进行了扩展。陈炎［17］在二自由度模型的基础上加入了侧倾运动修正，可以在仿真和参数辨识时简化运算。关龙新等［18］基于MPC算法提出了一种前馈双补偿抗扰动机制，然后通过扩张状态观测器实时估计车辆未知扰动量用于前馈补偿。然而，路径跟踪控制高度依赖于车辆动力学模型，因此如何建立更高精度的动力学模型，并运用于控制器设计仍需要开展进一步研究。

本文针对智能车辆路径跟踪控制器在高速大曲率工况下适应能力不足的问题展开研究。首先，引入悬架和转向系统的动态特性来修正横向动力学方程，建立车辆优化动力学模型；其次，推导了优化的预测模型，并设计了关于车辆速度与道路曲率的自适应预测时域策略，实现了预瞄距离实时调整的MPC控制；最后，通过CarSim/Simulink联合仿真验证设计控制器的有效性。

1  优化车辆动力学模型

1.1  经典动力学建模与静态稳定性因数分析

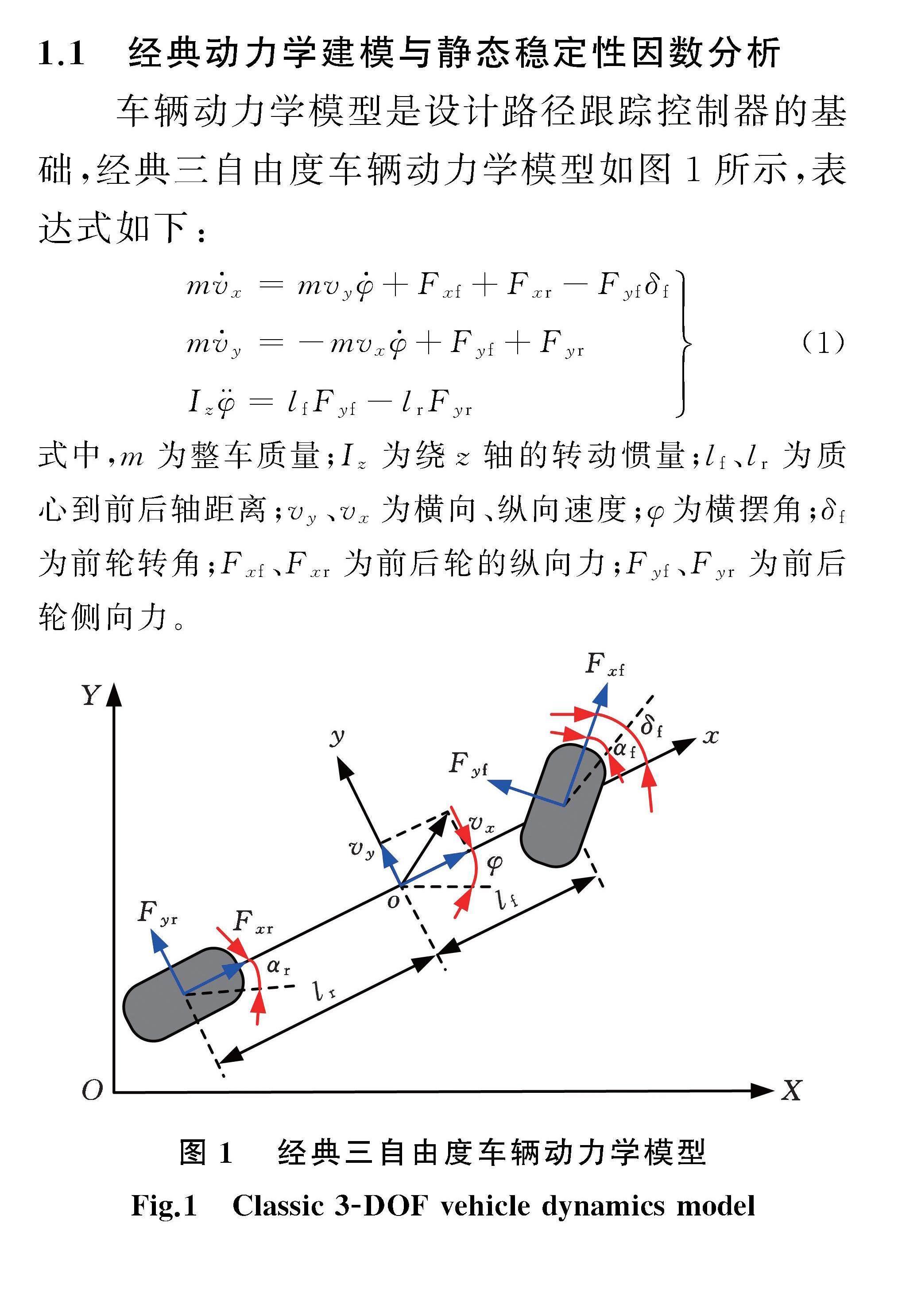
车辆动力学模型是设计路径跟踪控制器的基础，经典三自由度车辆动力学模型如图1所示，表达式如下：

mv·x=mvyφ·+Fxf+Fxr－Fyfδf

mv·y=－mvxφ·+Fyf+Fyr

Izφ¨=lfFyf－lrFyr（1）

式中，m为整车质量；Iz为绕z轴的转动惯量；lf、lr为质心到前后轴距离；vy、vx为横向、纵向速度；φ为横摆角；δf为前轮转角；Fxf、Fxr为前后轮的纵向力；Fyf、Fyr为前后轮侧向力。

前后车轮侧偏角分别为

αf=arctan（vy+lfφ·vx）－δf≈vy+lfφ·vx－δf（2）

αr=arctan（vy－lrφ·vx）≈vy－lrφ·vx （3）

稳态横摆角速度增益和静态稳定性因数分别为

φ·δf=vxL1+mL2（lfCαr－lrCαf）v2x  （4）

Ks=mL2（lfCαr－lrCαf） （5）

式中，L为轴距；Cαf、Cαr为前后轮侧偏刚度。

由式（2）～式（5）推导侧偏角与静态稳定性因数的关系为

δf=αf－αr+L/R=（1+Ksv2）L/R（6）

式中，v为车辆速度；R为行驶半径。

由式（6）可知，静态稳定性因数仅由车辆基础参数组成，忽略了悬架与转向系统的影响，而车辆在高速大曲率工况下会产生较大的载荷转移，悬架和转向系统结构会发生较大变形，静态稳定性因数精度会下降，经典动力学模型不能较好地体现车辆操控特性。

1.2  横向动力学优化及模型建立

在侧向加速度较大时，车辆悬架和转向系统变形会导致四轮定位参数变化，对车辆横向动力学产生较大的影响。目前的研究主要是通过算法的鲁棒性解决建模过程中产生的误差，但复杂的算法对控制系统的实时性要求提出挑战。本文将侧倾转向、侧倾外倾、变形转向和变形外倾产生的四轮定位参数变化补偿到动力学方程中，将试验数据和动力学机理融合进行建模，优化车辆的横向动力学。

在悬架K（kinematic）特性研究中，车辆侧倾会引起前转向轮绕主销的转动和后轮绕垂直于地面轴线的转动，即车轮束角会产生一个侧倾转向角的变化，如图2a所示。同时，车辆侧倾会引起车轮绕x轴的转动，即车轮外倾角会产生一个侧倾外倾角的变化，如图2b所示。在悬架C（compliance）特性研究中，悬架导向杆系元件在侧向力或回正力矩作用下发生变形，引起前轮绕主销的转动和后轮绕垂直于地面轴线的转动，即车轮束角会产生一个变形转向角的变化，如图2c、图2d所示。同时，变形也会引起车轮绕x轴的转动，即车轮外倾角会产生变形外倾角的变化，如图2e、图2f所示。

四轮定位参数变化系数如表1所示。一般假

设侧向力作用在轮胎的几何中心，但车辆实际在转弯中会产生轮胎拖矩TPF、TPR，影响质心到前后轴的距离。载荷转移（LLT）、车辆的驱动力或制动力和车身变形都会影响到稳定性因数。侧倾转向和变形转向产生的车轮束角变化可以等效为车轮转向角的几何修正，优化后的前后轮侧偏角分别为

αfo=vy+lfoφ·vx－（δf+kf1r+kf3Fyfo－kf5Mzfo）（7）

αro=vy－lroφ·vx－（kr1r+kr3Fyro－kr5Mzro）（8）

式中，Fyfo、Fyro为优化后的前后轮侧向力；Mzfo、Mzro为优化后的前后轮回正力矩；lfo、lro为优化后的质心到前后轴距离；r为车辆侧倾角。

车辆侧倾角与侧向加速度存在滞后的线性关系，于是可将车辆侧倾角转化为

φr=kay=k（v·y+vxφ·） （9）

式中，k为转换系数；ay为侧向加速度。

外倾角会让车轮具有绕旋转轴线与地面交点方向滚动的趋势，由于受车轴的约束两车轮一起前行，而轮胎在接地点会产生外倾力，于是车辆侧倾外倾和变形外倾产生的车轮外倾角变化可以等效为侧向力的力修正，前后轮的外倾力分别为

Fyfγ=Cγf（kf2r+kf4Fyfo－kf6Mzfo） （10）

Fyrγ=Cγr（kr2r+kr4Fyro－kr6Mzro） （11）

式中，Cγf、Cγr分别为前后轮外倾刚度；Fyfγ、Fyrγ分别为前后轮外倾侧向力。

联立式（7）～式（11），可得到优化后的前后轮侧向力Fyfo和Fyro，实现横向动力学的优化。

综上所述，融入车辆侧倾与悬架变形特性的优化动力学模型为

v·x=vyφ·+（Fxf+Fxr－Fyfoδfo）/m

v·y=－vxφ·+（Fyfo+Fyro）/m

φ¨=［（lf－TPF）Fyfo－（lr+TPR）Fyro］/Iz

X·=vxcos φ－vysin φ

Y·=vxsin φ+vycos φ（12）

式中，X·、Y·分别为车辆X、Y方向的速度。

1.3  优化动力学模型实车验证

本文目标车辆为某款畅销的纯电动微型汽车，车辆基础参数如表2所示。车辆满载工况下的悬架KC特性试验现场如图3所示。

表1中的优化系数通过加权最小二乘（WLS）法［19］估算，以侧倾转向系数为例，假设车辆侧倾角与车轮束角的关系函数为Ytoe=Xrollθ，则

Tj=1r11r21riτjkj（13）

i=1，2，…，n  j=fl，fr，rl，rr

式中，Ytoe为车轮束角；θ为待定系数；Xroll为车辆侧倾角；Tj为各车轮侧倾转向束角；τj为各车轮初始束角；kj为各车轮优化系数。

定义损失函数并求解系数矩阵如下：

J（θ）=12（XrollGθ－Ytoe）T（XrollGθ－Ytoe） （14）

θ=（XTrollGTRXroll）－1XTrollGTGYtoe （15）

式中，G为对角权重矩阵。

悬架KC试验数据与估计的优化系数如图4所示。车辆左转时，会压缩右前轮减小束角，伸长左前轮增加束角，从而增加不足转向；车辆右转时，会压缩右后轮增加束角，伸长左后轮减小束角，从而增加不足转向。转化为两轮模型的前轴侧倾转向系数kf1为0.1067，

后轴侧倾转向系数kr1为0.1617。同理可得其余优化系数。

基于式（6）～式（8）修正侧倾转向角，推导出由侧倾转向影响产生的扩展稳定性因数为

K1=－kf1r－kr1rLay （16）

基于式（6）～式（11），将车轮束角和外倾角变化依次转换为车轮转角修正，整理出动态稳定性因数Kd表达式为

δf+∑6i=1Δδfi－Δδri=LR（1+Ksv2） （17）

δf=LR［1+（Ks+∑6i=1Ki）v2］=LR（1+Kdv2） （18）

式中，Δδfi、Δδri分别为前后轮修正转向角；Ki为扩展稳定性因数。

该款微型电动车性能有限，进行侧向加速度为0.4g的定半径稳态回转试验如图5所示，根据试验数据计算得到扩展稳定性因数如图6所示。各扩展稳定性因数在动态稳定性因数中占比较大，侧倾与变形转向特性对车辆操纵稳定性影响显著，验证了建立优化动力学模型的必要性。

在操控稳定性试验中，车辆进行75 km/h的蛇形绕桩试验，采集的横摆角速度和侧向加速度数据与模型仿真数据比较如图7、图8所示，模型误差如图9、图10所示。车辆进行100 km/h的0.4g角阶跃输入瞬态试验，试验数据与模型仿真数据比较如图11、图12所示。数据表明，在蛇形绕桩试验中，与经典模型相比，优化模型的侧向加速度均方根误差下降40.2%，横摆角速度均方根误差下降48.8%，并且峰值误差大幅降低，误差统计如表3所示。在0.4g角阶跃输入试验中，优化模型的稳态侧向加速度误差下降59.4%，稳态横摆角速度误差下降66.7%，CarSim模型与实车试验数据吻合，可作为后续设计控制器的控制对象，优化动力学模型精度显著提高。

2  模型预测控制器（MPC）设计

2.1  基于优化动力学模型的MPC设计

基于前文的优化动力学模型设计路径跟踪控制器能够提高MPC精度，进一步设计自适应预测时域策略可提高控制器的鲁棒性，控制原理如图13所示。本文针对高速大曲率工况下路径跟踪问题，假设车辆纵向保持高速，仅控制前轮转角。选取式（12）的状态向量ξ=（vy，vx，φ，φ·，Y，X）T，控制量u=（δf），输出量η=（φ，Y，X）T。将模型线性化，将ξ·=f（ξ，u）在工作点（ξr，ur）一阶泰勒展开并忽略高阶项，得

ξ·=f（ξr，ur）+fξ（ξ－ξr）+fu（u－ur）（19）

联立式（12）与式（19），通过一阶差商法得到离散系统模型：

ξ（k+1）=Akξ（k）+Bku（k）+dk（20）

η（k）=Ckξ（k）（21）

式中，Ak为状态矩阵；Bk为输入矩阵；dk为模型误差补偿;Ck为输出矩阵。

将式（20）、式（21）中对前轮转角的控制转变

为对转角增量的控制，扩展状态量得到新的状态空间为

ξ～（k+1|t）=A～kξ～（k|t）+B～kΔu（k|t）+d～k

η（k|t）=C～kξ～（k|t）

ξ～（k|t）=（ξ（k|t），u（k－1|t））T（22）

MPC通过预测模型计算系统预测时域Np内的输出，通过求解满足目标函数及各种约束的优化问题，得到控制时域Nc内的控制序列。基于优化动力学模型推导的优化预测矩阵为

H（t）=Ψξ（t）+ΘΔU（t）+ΓΦ（t）（23）

H（t）=η（k+1）η（k+2）η（k+Nc）η（k+Np）ΔU（t）=Δu（k）Δu（k+1）Δu（k+Nc－1）

式中，H（t）为预测输出序列；ΔU（t）为控制输入序列；Ф（t）为测量误差序列；Ψ、Θ和Γ为状态空间递推矩阵。

设计目标函数和约束条件如下：

J=min∑Npi=1‖η（k+i|t）－ηref（k+i|t）‖2Q+

∑Nc－1i=0‖Δu（k+i|t）‖2R+ρε2（24）

－δf，lim≤δf≤δf，lim

－Δδlim≤Δδ≤Δδlim

－βlim≤β≤βlim

－ay，min－ε≤ay≤ay，max+ε

－αlim≤αf，r≤αlim（25）

式中，Q、R为权重矩阵；ρ为松弛因子权重系数；ε为松弛因子。

目标函数优化求解问题可以转化为标准二次型规划问题，求解得到控制增量序列和松弛因子。选择控制增量序列第一个元素反馈给系统并重复上述过程，实现滚动优化控制。

2.2  自适应预测时域策略

MPC算法中的预测时域参数对智能车辆路径跟踪效果影响显著。不同车速下对控制器预测时域的选择有不同的要求［11］。在低速工况下，对车辆操控稳定性要求不高，偏小的预测时域有更好的控制效果，增大预测时域可能会降低跟踪精度。反之，在高速工况下，对车辆操控稳定性要求较高，增大预测时域能获取更远的道路信息以保证车辆的稳定性，减小预测时域可能会导致转向抖动。同时，预测时域的选择还需考虑前方道路的曲率信息，特别是在高速大曲率极限工况下，应根据预瞄距离内的道路曲率实时调整预测时域，以避免过多的车道偏离。综上所述，极限工况下预测时域需要依据车速及道路曲率实时调整。

本文通过测试智能汽车在双移线路径上的跟踪能力验证控制器的优化效果。参考路径如图14所示［20］，期望横摆角如图15所示，表达式为

Yref=dy1（1+tanh（z1））－dy2（1+tanh（z2））

z1=shdx1（X－x1）－sh2

z2=shdx2（X－x2）－sh2（26）

φref=arctan（dy1shdx1cosh2（z1）－dy2shdx2cosh2（z2）） （27）

式中，Yref为期望横向位置；φref为期望横摆角；dx1、dx2、dy1、dy2和sh为双移线调整参数。

基于曲率公式定义预瞄距离内的道路弯曲度（mean road curvature， MRC）：

ρMRC=1Np∑Npi=1|Y¨ref（Xi）|（1+Y·ref（Xi）2）32（28）

式中，Y·ref（Xi）、Y¨ref（Xi）分别为预瞄点的一阶、二阶导数。

高速工况下需要考虑控制器的实时性，自适应预测时域策略应避免复杂计算。基于二维高斯函数的集中性和均匀变动性，设计预测时域关于车速与道路弯曲度的函数：

Np=round（Aexp（（v－vmax）2σ21+ρ2MRCσ22）） （29）

式中，A为预测时域上限；vmax为车速上限；σ1为车速影响因子；σ2为道路弯曲度影响因子。

根据车辆特性标定参数得到预测时域离线数据库，其三维分布如图16所示。

3  试验仿真分析

3.1  仿真环境

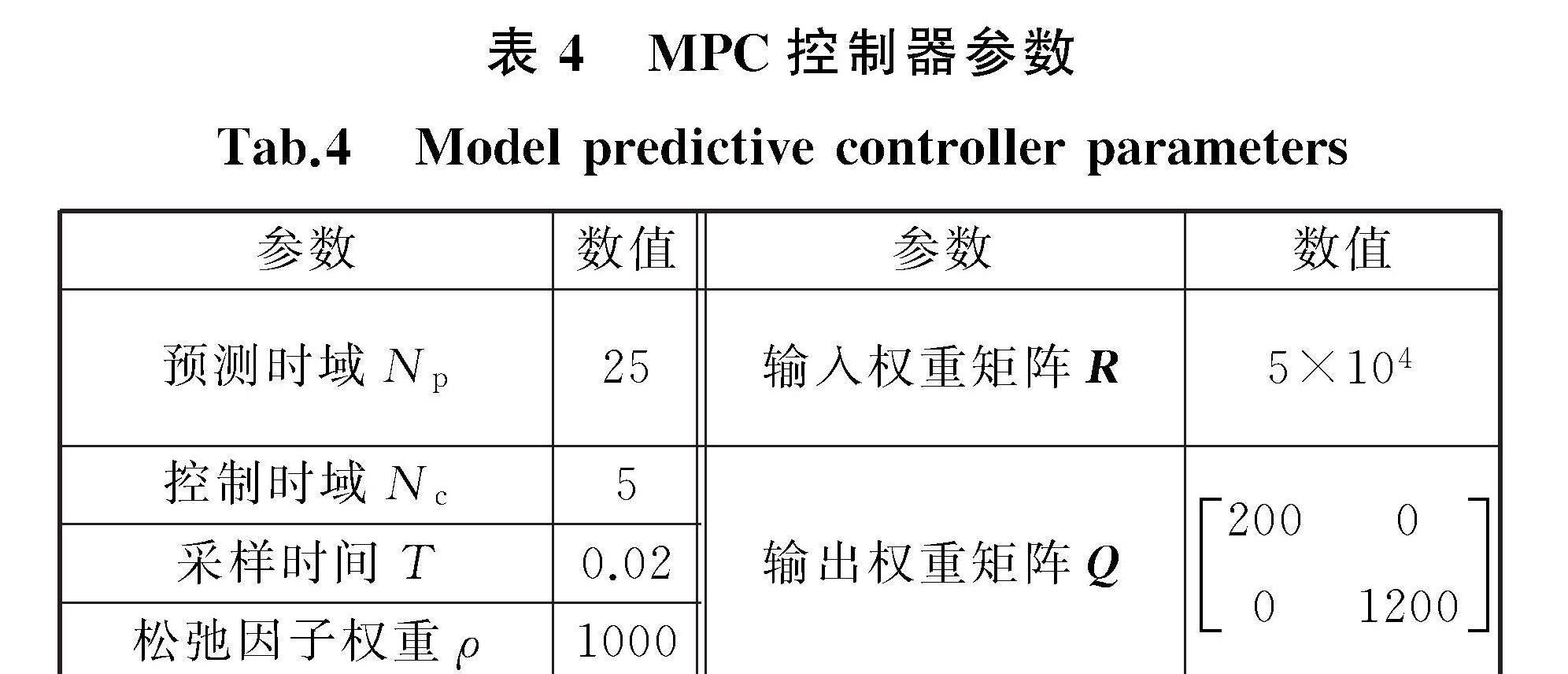
基于CarSim/Simulink搭建联合仿真平台，验证本文提出的优化控制策略。对比分析基于经典动力学模型的MPC控制（traditional dynamic model-MPC， TR-MPC）、基于优化动力学模型的MPC控制（optimizing dynamics model-MPC， OM-MPC）和基于优化动力学模型的自适应预测时域MPC控制（optimizing dynamics model-adaptive prediction horizon-MPC，OM-AP-MPC）在双移线道路上的跟踪精度和车辆稳定性。该微型电动车最高时速为100 km/h，本文高速工况选取72 km/h，中低速工况选取54 km/h。假定路面高附着系数为0.85，低附着系数为0.45。MPC控制器初始参数如表4所示。

3.2  结果分析

车速v=72 km/h且附着系数μ=0.85的高速工况下，跟踪误差曲线如图17、图18所示。车速为v=54 km/h且附着系数μ=0.45的低附工况下，跟踪误差曲线如图19、图20所示。高速或低附着工况下，车辆过弯时呈现明显的侧倾和变形转向特性，OM-MPC控制器输出更加精确的控制量，有效降低了路径跟踪横向误差和横摆角误差。

高速大曲率工况下，图18中OM-MPC控制器在50～100 m的出弯处车辆横摆角波动依旧较大。引入OM-AP-MPC控制器，各控制器期望路径和期望横摆角跟踪曲线如图21、图22所示。图23、图24中，OM-MPC和OM-AP-MPC控制器能有效减小横向误差、横摆角误差的峰值。自适应预测时域策略提高了路径跟踪精度和车辆稳定性，使车辆在75～100 m处快速收敛至直道。

本文设计的三种控制器误差统计如表5所示。相比于TR-MPC控制，本文提出的OM-AP-MPC控制器路径跟踪误差的平均值降低37.8%，横摆角误差的平均值降低60.3%，控制效果得到了显著提升。

图25为横摆角速度质心侧偏角相位图，由图可见，OM-AP-MPC控制器相图所占面积最小，表明车辆的质心侧偏角在相同横摆角速度下被控制在更小的范围内，操控稳定性得到了提升。图26为道路弯曲度及预测时域变化曲线，随着道路弯曲度的变化，预测时域能够实时计算调整，提高了跟踪精度并加快了误差收敛速度。

4  结论

（1）针对一般路径跟踪控制器在高速大曲率工况下适应性不足的问题，本文提出了一种基于优化动力学模型的自适应预测时域模型预测控制策略。

（2）通过蛇形绕桩和0.4g角阶跃实车操稳性实验验证，优化动力学模型能更精确地体现车辆状态。通过双移线道路仿真实验验证，基于优化动力学模型的模型预测控制效果显著优于一般模型预测控制器，进一步引入自适应预测时域策略，可提高车辆的跟踪精度和稳定性。

（3）本文在仿真环境下初步验证了基于优化动力学模型的自适应预测时域MPC控制（OM-AP-MPC）的效果，为解决高速大曲率等极限工况下的路径跟踪问题提供了新的思路。

参考文献：

［1］  边明远， 李克强. 以智能网联汽车为载体的汽车强国战略顶层设计［J］. 中国工程科学， 2018， 20（1）：52-58.

BIAN Mingyuan， LI Keqiang. Strategic Analysis on Establishing an Automobile Power in China Based on Intelligent & Connected Vehicles［J］. Strategic Study of Chinese Academy of Engineering， 2018， 20（1）：52-58.

［2］  熊璐， 杨兴， 卓桂荣， 等. 无人驾驶车辆的运动控制发展现状综述［J］. 机械工程学报， 2020， 56（10）：127-143.

XIONG Lu， YANG Xing， ZHUO Guirong， et al. Review on Motion Control of Autonomous Vehicles［J］. Journal of Mechanical Engineering， 2020， 56（10）：127-143.

［3］  金辉， 李世杰. 基于极限车速的车辆稳定性控制研究［J］. 汽车工程， 2018， 40（1）：48-56.

JIN Hui， LI Shijie. A Research on Vehicle Stability Control Based on Limited Speed［J］. Automotive Engineering， 2018， 40（1）：48-56.

［4］  王京起， 陈慧岩， 郑培. 应用模糊自适应PID和预瞄策略的自主车辆转向控制［J］. 汽车工程， 2003， 35（4）：367-371.

WANG Jingqi， CHEN Huiyan， ZHENG Pei. Application of Fuzzy Adaptive PID and Previewing Algorithm in Steering Control of Autonomous Land Vehicle［J］. Automotive Engineering， 2003， 35（4）：367-371.

［5］  ZHAO Pan， CHEN Jiajia， SONG Yan， et al. Design of a Control System for an Autonomous Vehicle Based on Adaptive-PID［J］. International Journal of Advanced Robotic Systems， 2012， 9（2）：51314.

［6］  郭景华， 李琳辉， 胡平， 等. 基于模糊逻辑的无人驾驶车纵向多滑模控制［J］. 中国公路学报， 2013， 26（1）：170-176.

GUO Jinghua， LI Linhui， HU Ping， et al. Longitudinal Multiple Sliding-mode Control of Unmanned Vehicle via Fuzzy Logic［J］. China Journal of Highway and Transport， 2013， 26（1）：170-176.

［7］  丛森森， 高峰， 许述财. 基于动态稳定域的车辆横纵向稳定性协同控制［J］. 汽车工程， 2022， 44（6）：900-908.

CONG Sensen， GAO Feng， XU Shucai. Cooperative Control of Vehicle Lateral and Longitudinal Stability Based on Dynamic Stability Region［J］. Automotive Engineering， 2022， 44（6）：900-908.

［8］  WANG Rongrong， JING Hui， HU Chuan， et al. Robust H∞ Path Following Control for Autonomous Ground Vehicles with Delay and Data Dropout［J］. IEEE Transactions on Intelligent Transportation Systems， 2016， 17（7）：2042-2050.

［9］  龚建伟， 姜岩， 徐威. 无人驾驶车辆模型预测控制［M］. 北京：北京理工大学出版社，2014：57-59.

GONG Jianwei， JIANG Yan， XU Wei. Model Predictive Control of Self-driving Vehicles［M］. Beijing：Beijing Institute of Technology Press， 2014：57-59.

［10］  ONIEVA E， NARANJO J E， MILANS V， et al. Automatic Lateral Control for Unmanned Vehicles via Genetic Algorithms［J］. Applied Soft Computing， 2011， 11（1）：1303-1309.

［11］  张世义， 顾小川， 唐爽， 等. 采用变时域模型预测的车辆路径跟踪控制方法［J］. 华侨大学学报（自然科学版）， 2021， 42（2）：141-149.

ZHANG Shiyi， GU Xiaochuan， TANG Shuang， et al. Vehicle Path Tracking Control Method Using Varying Horizon of Model Predictive Control［J］. Journal of Huaqiao University（Natural Science）， 2021， 42（2）：141-149.

［12］  LIU Kai， GONG Jianwei， CHEN Shuping， et al. Model Predictive Stabilization Control of High-speed Autonomous Ground Vehicles Considering the Effect of Road Topography［J］. Applied Sciences， 2018， 8（5）：822.

［13］  白国星， 孟宇， 刘立， 等. 基于可变预测时域及速度的车辆路径跟踪控制［J］. 中国机械工程， 2020， 31（11）：1277-1284.

BAI Guoxing， MENG Yu， LIU Li， et al. Path Tracking Control of Vehicles Based on Variable Prediction Horizon and Velocity［J］. China Mechanical Engineering， 2020， 31（11）：1277-1284.

［14］  CHEN B C， TSAI C T， LEE K. Path-following Steering Controller of Automated Lane Change System with Adaptive Preview Time［C］∥2015 IEEE International Conference on Systems， Man， and Cybernetics. Hong Kong， 2015：2522-2526.

［15］  余志生. 汽车理论［M］. 北京：机械工业出版社，2008：144-146.

YU Zhisheng. Automobile Theory［M］. Beijing：China Machine Press， 2018：144-146.

［16］  刘文营， 刘伟， 崔晓川. 二自由度车辆动力学模型的扩展研究［J］. 中国测试， 2016， 42（增刊2）：76-79.

LIU Wenying， LIU Wei， CUI Xiaochuan. Research on Extension of Two Degree of Freedom Vehicle Dynamics Model［J］. China Measurement & Test， 2016， 42（S2）：76-79.

［17］  陈炎. 汽车转向动力学的改进的二自由度数学模型及其参数辨识［J］. 车辆与动力技术， 1990， 12（2）：45-52.

CHEN Yan. Improved Two-degree-of-freedom Mathematical Model and Parameter Identification of Vehicle Steering Dynamics［J］. Vehicle & Power Technology， 1990， 12（2）：45-52.

［18］  关龙新， 顾祖飞， 张超， 等. 考虑系统复杂扰动的智能车模型预测路径跟踪控制［J］. 汽车工程， 2022， 44（12）：1844-1855.

GUAN Longxin， GU Zufei， ZHANG Chao， et al. Model Predictive Path Following Control of Intelligent Vehicles Considering System Complex Disturbances［J］. Automotive Engineering， 2022， 44（12）：1844-1855.

［19］  麦尔斯. 经典和现代回归分析及其应用［M］. 北京： 高等教育出版社，2015.

MYERS R H. Classical and Modern Regression with Applications［M］. Beijing：Higher Education Press， 2015.

［20］  FALCONE P， ERIC TSENG H， BORRELLI F， et al. MPC-based Yaw and Lateral Stabilisation via Active Front Steering and Braking［J］. Vehicle System Dynamics， 2009， 46（1）：611-628.

（编辑  王艳丽）

作者简介：

何智成，男，1983年生，教授、博士研究生导师。研究方向为智能汽车与智能控制、先进结构与智能设计。E-mail：hezhicheng815@163.com。

韦宝侣（通信作者），男，1978年生，博士研究生。研究方向为智能底盘与转向系统。E-mail：Baolv.wei@sgmw.com.cn。