多元拓展变式教学 有效落实核心素养

李杉

摘要：多元变式教学在初中数学日常教学实践中的应用，不仅能够有效增强学生举一反三的能力，自然推动学生发散思维和创新思维的萌发与发展，还可以有效锻炼其解题技巧与能力，提高解题效率.文章提出多元变式教学需关注基础性、思维性、开放性及层次性，这样方能有效落实数学核心素养.

关键词：变式教学；核心素养；数学思维

伴随着教育领域课程改革的持续推进和深入开展，一线教师已经能够针对多元变式教学在初中数学课堂教学中的关键教学价值和重要意义进行深入研究，且形成了深刻的认识.从实践过程来看，多元变式教学在初中数学日常教学实践中的应用，不仅能够有效增强学生举一反三的能力，自然推动学生发散思维和创新思维的萌发与发展，还可以有效锻炼其解题技巧与能力，提高解题效率.下面结合具体教学实践进行分析与阐述.

1 关注基础性：聚焦基础，有效提升

基础知识和基本概念是引领问题解决、生成新问题的起点.基于知识发生的过程设计问题，用凸显知识形成过程与来龙去脉的基础性变式，引领学生自主归纳得出知识间最本质的内涵，从而在夯实基础的同时促进思维的有效提升.当然，教育是慢的艺术，在变式教学中，教师在关注基础性的同时还需注重适度性，以适量的题目设计和适中的讲解速度相结合，并给予学生充足的探究时空，让低起点的变式达到较高立意，促进学生的有效发展.

例1 试求出16的算术平方根.

变式1 试求出16的平方根.

变式2 试求81的平方根.

变式3 已知a的算术平方根为2，试求a.

问题是启迪思维的载体，可以激发想象力，引领思维的深入与发散.以上例题通过借题发挥，不断变化问题的角度，或变结论、或变条件、或变问法，引领学生拾级而上地解决问题，在有效夯实数学基础的同时打破思维定势，拓宽解题视野，最终在实现知识进阶的过程中达到思维的拔节.

2 关注思维性：深度思考，形成创新

创新思维需要在直观操作、猜测联想、渐深探索等过程中加以培养，而发展学生的创新思维可助力学生独到见解的形成，使数学学习逐步深入.用变式教学引领学生创新思维的发展是每个教师的致力追求.这就需要教师在实际教学的过程中，注重变式的思维性，通过一般性的变式设计方式，如变问法、变位置等，呈现变式的思维性和多元化，助力学生建模思维的培养，从而发挥变式教学的价值与意义，让学生把握变中不变的本质，探寻出变的规律，继而提升解题能力，完善认知结构，促进创新意识的发展.

例2 已知一次函数与反比例函数图象相交于点M（－3，2），N（2，n）.

（1）分别求出上述两个函数关系式；

（2）将（1）的图象画在同一平面直角坐标系中，并据此阐述使一次函数值大于反比例函数值的x的取值范围.

变式1 不改变例2的题设以及第（1）问，并在画出图象后阐述使得一次函数值小于反比例函数值的x的取值范围.

变式2 已知一次函数与反比例函数的图相交于点M（－3，2），N（2，n），试判断∠MON的取值范围，并求出△MON的面积.

变式3 已知一次函数与反比例函数的图象相交于点P（－2，1），Q（－1，m）.

（1）将它们的图象画在同一平面直角坐标系中，并据此分别阐述使得一次函数值小于和大于反比例函数值的x的取值范围；

（2）判断∠POQ的取值范围，并求出△POQ的面积.

例3 分解因式：a2+5ab+6b2.

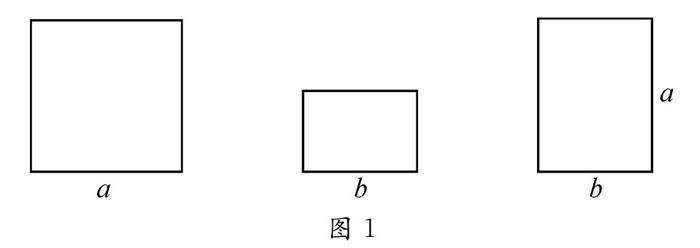
变式 如图1，已知一正方形的边长是a，另一正方形边长是b，若想拼出一个面积是a2+5ab+6b2的长方形，还需几个长和宽分别是a和b的长方形？

题海战术只会让学生在盲目练习中迷失方向，让学生有限的学习时空得不到保障.创新是引领发展的动力，有效激发和善于运用创新思维，可以将创新思维转化为促进数学核心素养发展的强大动力.以上思维性变式题组中，例2通过变结论、延伸结论及改变条件位置，拾级而上地引领学生多角度地思考和探究问题，在公式的灵活运用与拓展中极好地激发了创新思维的火花，让数学学习更高效；例3则是极好地渗透数形结合的思想，让学生在数与形的沟通中发展个性，深化认知，发展创新思维能力.

3 关注开放性：突破难点，体味价值

我们的课堂教学应善于变化，深度挖掘例习题的教育功能，通过变新、变深来引领学生突破难点，体味数学学习的乐趣与价值.这就需要教师在变式教学中注重变式的开放性，引导学生从各种途径解决问题，并探寻解决问题的通性通法.当然，在解决问题的过程中，教师也可以增强教学的透明度来暴露学生的思维过程，这样一来，则可以让学生的思路更开阔，并能熟练掌握知识间的内在联系，培养思维的灵活性和开放性.

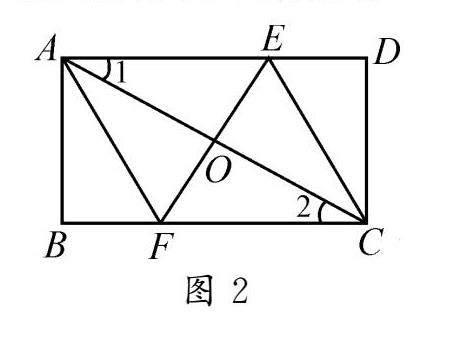
例4 如图2，已知矩形ABCD的对角线AC的垂直平分线分别交边AD，BC于点E，F.证明：四边形AFCE为菱形.

变式1 将例4题设中的矩形改为“梯形”，其余条件均不改变，同样证明：四边形AFCE为菱形.

变式2 折叠矩形ABCD使得A，C两点重合，得到折痕EF.证明：四边形AFCE为菱形.

变式3 在不改变例4题设的情况下，添加题设“且AB=6，AD=8”.试求出四边形AFCE的面积.

变式4 在不改变例4题设的情况下，添加题设“且AE=10，△ABF的面积为24”，试求△ABF的周长.

学生的数学学习需要丰富的营养，这些营养蕴藏在问题之中，需要教师在理解数学、理解教学、理解学生的基础上加以挖掘和运用.此处，在习题练习之后教师采用变图形、变条件、延伸结论等方式设计开放性变式，引领学生深度思考、联想和探究.这样的变式训练有着丰富的内涵，不仅极好地夯实了双基，还有效突破了难点，增强了学生的解题能力，更在知识的横向联系与纵向延伸下有效地提升了学习质效，形成理性思维［1］.

4 关注层次性：层层递进，深化理解

同一题型的反复练习易让学生产生思维惰性，长此以往常常使得学生的思维无法得到更深、更广的发展，造成课堂教学低效的不良后果.因此，在变式教学中，教师需关注到层次性，让学生在层层递进的问题引领下踏梯而上，深化理解知识的同时提高分析和解决问题的能力，发展学生的智力和学科素养［2］.

例5 已知a+b=3，ab=2，试求a2+b2.

变式1 已知a－b=1，a2+b2=25，试求ab.

变式2 已知a+b=3，ab=2，试求a4+b4.

变式3 已知（a+b）2=1，（a－b）2=49，试求a2+b2及ab的值.

变式4 已知长方形ABCD的周长为40，面积为75，若以长方形ABCD的长和宽分别为边长构造正方形，试求构造得到的两个正方形的面积之和.

变式5 已知长方形ABCD面积为12，且两边之差为4，若以长方形ABCD的长和宽之和为边长构造正方形，试求构造得到的正方形的面积.

变式6 已知一直角三角形的斜边长是13，两条直角边之和是17，，试求该直角三角形的面积.

变式7 已知菱形ABCD的周长是2a，对角线AC，BD相交于点O，且有AC+BD=b，试求菱形ABCD的面积.

关注变式的层次性可以让学生在低起点、高立意的数学探究中深化理解，建立信心.这里也正是因为这样的层次性变式，让学生试着“跳一跳、摘果子”，使其在深度探究中体验成功的乐趣和喜悦，继而逐步树立学习的信心，促进良性循环，无痕发展数学核心素养［3］.

总之，运用好借题发挥这种灵活而创新的教学策略，采用多元拓展变式教学，可以拓宽学生的视野，开拓创新思维，发展数学核心素养.

参考文献：

［1］徐军.初中数学教学中理性思维能力的培养［J］.数理化解题研究，2022（23）：2-4.

［2］温河山.初中数学变式教学的方法探析［J］.课程教学研究，2012（10）：48-50，54.

［3］尤善培.围绕核心 主动变式——数学“变式教学”的实践与思考［J］.数学通报，2016，55（2）：17-19，24.