例谈用一元二次方程求根公式解难题

袁祖军

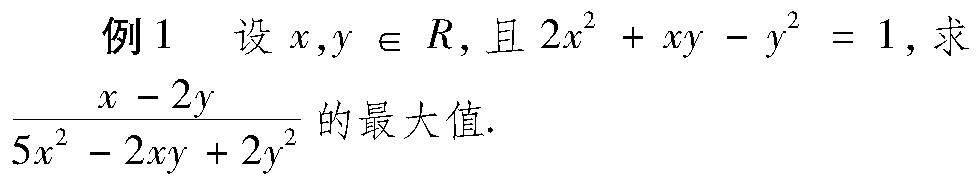
求根公式解含参一元二次方程，结果一般都比较繁（两个根都是二次根式代数式），用于计算会更繁，往往被认为是笨拙的解法而不被看好，特别是难题，一般都不考虑用求根公式解决，其实，有些难题用求根公式解并不难，本文通過两个例说明.

本题是一类常见的二元函数t=G（x，y）（F（x，y）=0）最值问题，通常的解法是技巧性很强的基本不等式法，即下面的解法1和解法2.

评注：上述解法1既有不好想的平方齐次化和“1”的巧代换，还有不好想的配凑均值不等式，更有取等条件的艰难确定，运算也未见简单；解法2直接换元，消元化为一元显函数，再换元化为简单函数求最值，思路自然，但也不简单.本题的自然直接的解法是用求根公式在约束条件方程中解出一元代入目标消元化为一元显函数求最值，即下面的解法3.

评注：解法3是最自然（好想）的方法（直接在约束条件方程中用一元二次方程求根公式解出一元代入目标消元化为一元显函数求最值，只要约束条件方程是可化为可解的二次方程（一次方程更不必说），在有导数知识下就总是可行的解法），且是本文三种方法中最简单的.

例2 已知实数x，y满足x2+2y2－xy=8，求x2+y2+xy的最大值.

用一元二次方程求根公式自然，简单.

总之，二次方程总是可用求根公式（配方法结果）解的，判别式和基本不等式（均值不等式，柯西不等式，权方和不等式）都是x2≥0（x∈R）产生的（文［1］），所以，用求根公式解决二次方程问题是自然的，不一定是很繁的 ，有时还是最简单的（文［2］），当技巧性的方法难想时，不妨先试试这个自然的方法.

参考文献

［1］熊福州.再探一新母不等式的普遍意义与应用［J］，河北理科教学研究，2020（04）10-11.

［2］熊福州.也谈解题应追求简单、自然［J］，河北理科教学研究，2005（03）3-5.