一次“说题”活动的实录与思考

谷红霞 谢辉

【摘  要】  针对教育教学研讨中的“说题”活动进行了研究，以实录的形式对“说题”这类活动涉及的关键环节展开分析，结合教育教学实践深入探讨：题目命制的来源、析题过程中的问题设置、反思过程中的联系性，基于整体观下将微专题意识贯穿说题活动始终.

【关键词】  说题；立体几何；动点；微专题

当前，教研活动中有一类“说题活动”受到广泛关注，旨在将“命题”“解题”“教题”“教学反思”融为一体，是一种反思性的教学活动［1］.由于题目本身既要讲给学生又要说给同行，因此，既要考虑学生的认知规律和教学的实际情况，又要从高等数学的视角下揭示题目背后数学知识的本质，非常利于促进教师的专业成长.

说题一般包括如下环节：说背景分析、说题目来源、说思路分析、说教学启示.目前，对于说题的一般流程，还没有公认的模式，因此说题的具体过程往往含有教师的个人色彩，是一种再创造的过程.因此“说题”这一教研活动能够引领教师更好地思考“如何命题能够考查学生对数学知识本质的理解”.长此以往，可以间接促进教师对教、学、评一体化的思考.

下面以“立体几何中的一类动点问题”为例，从“背景分析与教学体会、思路分析与教学联想、拓展分析与教学启示”三个方面对一道题目展开说明.其中，背景分析与教学体会中包含题目所涉及的教学内容和考试方向的分析，也含有教师在教学实践中了解到的学情、及根据学情应如何析题.思路分析与教学联想中包含试题编制的始末，以命题立意为主要脉络、一般方法为抓手，不同的解决思路与方法层层递进，从“好想”（直观）到“好算”（抽象），逐渐明晰“利用投影向量的模求距离”这一通法，实现“陌生问题熟悉化”及“琐碎知识系统化”.拓展分析与教学启示中包含问题变式和教学启示，既能突出对所讨论问题的强化、引申双重功能，又可凸显教师对析题教学的认识.

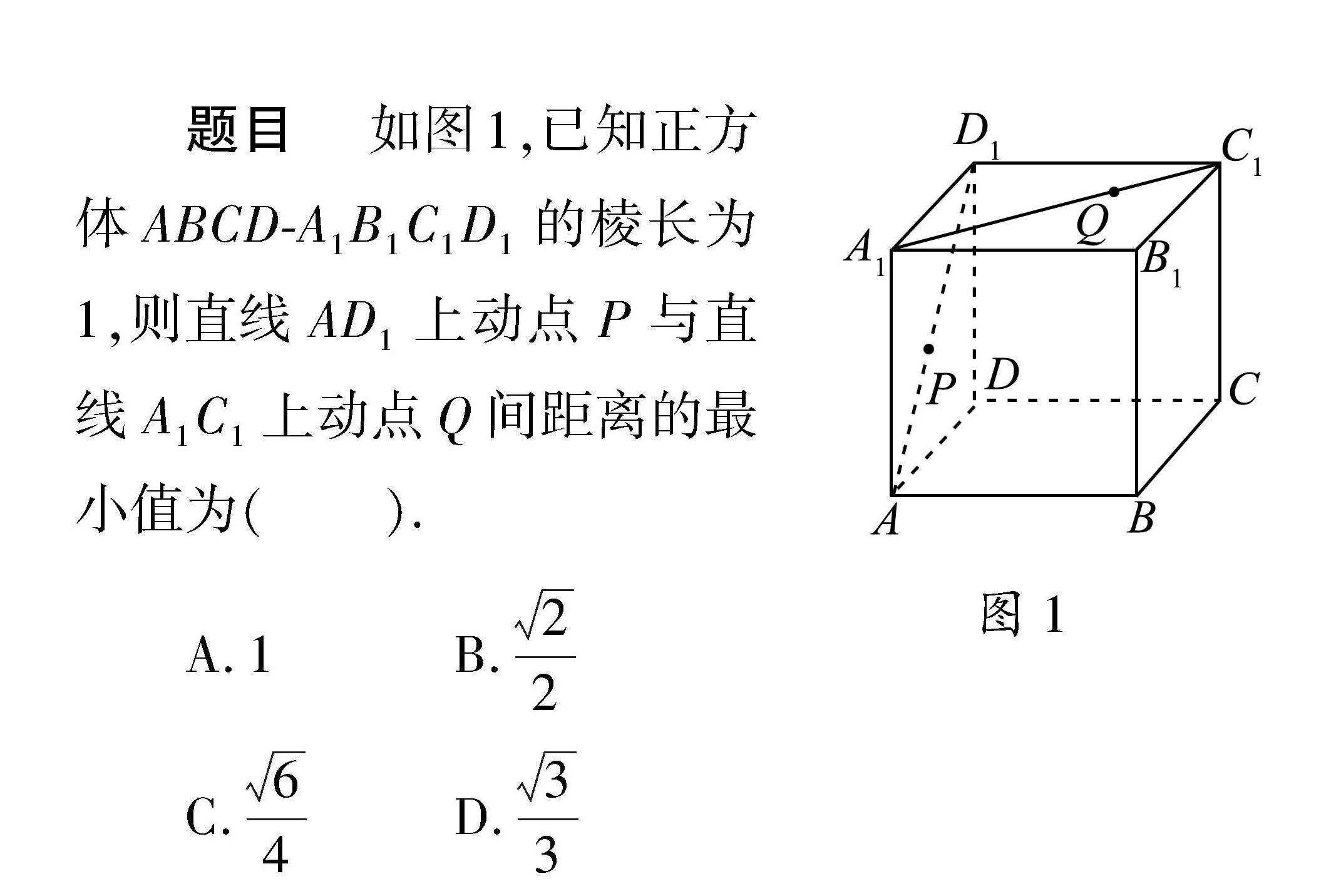
图1题目  如图1，已知正方体ABCD-A1B1C1D1的棱长为1，则直线AD1上动点P与直线A1C1上动点Q间距离的最小值为（  ）.

A.1    B.22

C.64

D.33

1  背景分析与教学体会

1.1  内容分析

从知识体系上看，“几何与代数”是高中数学的主线之一.

必修课程中“几何与代数”包括平面向量及其应用、复数、立体几何初步三部分.其中立体几何初步要求学生：能够运用图形的概念描述图形的基本关系和基本结果，能够证明简单的几何命题，并会进行简单应用.选择性必修课程中“几何与代数”包括空间向量与立体几何、平面解析几何两部分.其中空间向量与立体几何部分要帮助学生：运用空间向量研究立体几何中图形的位置关系和度量关系，体会向量方法和综合几何方法的共性和差异，运用向量方法解决简单的数学问题和实际问题［2］.

因此，在命题中应突出几何直观与代数运算之间的融合，即通过形与数的结合，凸显数学知识之间的关联，引导学生加强对数学整体性的理解.

1.2  考试分析

《高中数学课程标准（2017年版2020修订）》明确指出：这一主线的教学重点是要提升直观想象、逻辑推理、数学运算和数学抽象的素养.

从近三年高考试题和模拟试题的选填题看，命题都突出对“灵活选择运用向量方法与综合几何方法”的考查（具体题目略）.

1.3  学情分析

在教学实践中发现：学生面对立体几何中的動点问题，常望而生畏.一方面，运用综合法解决立体几何问题，往往需要挖掘位置关系，而学生却经常想不到；另一方面，运用向量法解决立体几何问题，则需要恰当地借助向量将几何问题转化为代数运算，而运动变化使得运算过程中含有一个或多个变量，这也是一些同学感到棘手之处.

1.4  教学体会

在析题过程中，要注重引导学生用自然语言描述运动变化的过程、分析引起变化的关键对象、用符号表示几何对象、抓住特殊位置与特殊关系、探索运动变化中的不变性，通过几何综合法或代数运算法解决问题.

2  思路分析与教学联想

2.1  试题来源

《人教A版高中数学第二册》拓广探索［3］中：启发学生在运动变化中思考位置关系的不变性（如图2），这使笔者联想到是否可以创编试题：启发学生在运动变化中思考度量关系的变化规律.

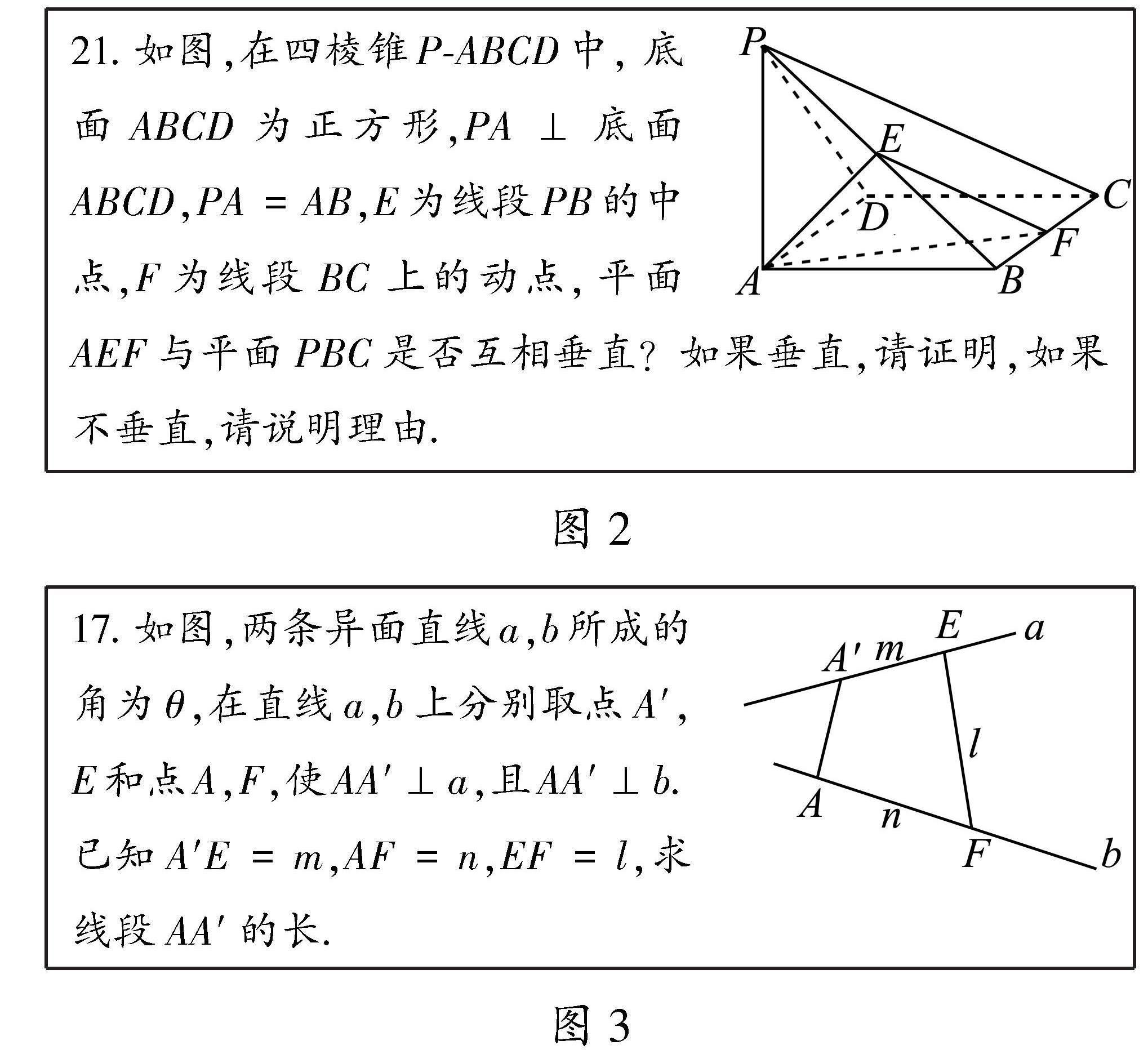
21.如图，在四棱锥P-ABCD中， 底面ABCD为正方形，PA⊥底面ABCD，PA=AB，E为线段PB的中点，F为线段BC上的动点，平面AEF与平面PBC是否互相垂直？如果垂直，请证明，如果不垂直，请说明理由.

17.如图，两条异面直线a，b所成的角为θ，在直线a，b上分别取点A′，E和点A，F，使AA′⊥a，且AA′⊥b.已知A′E=m，AF=n，EF=l，求线段AA′的长.

图3

《人教A版高中数学选择性必修第一册》拓广探索［4］中：启发学生用综合几何法求两异面直线间公垂线段的长（如图3），这使我联想到是否可以创编试题：启发学生在运动变化中探求两动点间距离变化规律.

一方面，正方体是研究空间位置关系的重要模型，以其为载体考查位置关系和度量关系，利于学生灵活运用多种方法解决问题，发展几何直观素养.另一方面，借助其各条面对角线，可讨论线与线间的平行、相交、异面三种位置关系.而本题目正是以异面直线为依托引出的动点问题，考查灵活运用向量法与综合几何法解决问题的能力.

2.2  思路分析

针对这一问题，首先，要利用图形描述、分析问题，建立起形与数的联系，探索解决问题的思路.

问题1  你能建立坐标系，利用两点间的距离公式求出两动点间距离的最小值吗？

思路与方法1   直接用两点间的距离公式.

图4分析  如图4，建立空间直角坐标系D-xyz.

设AP=λAD1=λ（－1，0，1）=（－λ，0，λ），λ∈R，则DP=DA+AP=（1－λ，0，λ）.

设A1Q=μA1C1=μAC=μ（－1，1，0）=（－μ，μ，0），μ∈R，则DQ=DA1+A1Q=（1，0，1）+（－μ，μ，0）=（1－μ，μ，1），

那么QP=DP－DQ=（μ－λ，－μ，λ－1），QP 2=（μ－λ）2+μ2+（λ－1）2=2μ2－2λμ+2λ2－2λ+1.

这里，先将μ看作主元，将上述二元二次函数看作关于μ的一元二次函数，配方：

QP 2=2（μ－12λ）2+（32λ2－2λ+1）.

当μ=12λ时，QP 2=32λ2－2λ+1，此时，当λ=23时，函数取得最小值.

故λ=23，μ=13时，QP 2=13，即动点P与动点Q的距离的最小值为33.

此题中有两个动点，于是距离的函数中含两个变量，可以将其中一个看作主元，再进行配方等代数运算.

当构建了这一解决问题的思路后，就加深了对异面直线这一类位置关系的认识.而这种直观想象会促进我们发现和提出问题，是进一步分析和解决问题的重要手段.

将μ看作主元就是点Q动，将λ看作常数就是将动点P看作定点，将两个动点的问题化归为一个动点，将几何中动中觅静的策略与代数运算中确定主元的方法相联系，从而引发进一步思考.

问题2  当点Q运动时，定点P与动点Q的最小距离是什么呢？

思路与方法2  利用点到直线的距离公式.

分析  建系同法一，A1C1=（－1，1，0），AP=（－λ，0，λ），AA1=（0，0，1）.

A1P=AP－AA1=（－λ，0，λ－1）.

与A1C1共线的单位向量e=A1C1A1C1=12（－1，1，0）=（－12，12，0）.

点P到直线A1C1的距离：

d=A1P 2－（A1P·e）2=λ2+（λ－1）2－λ22=32λ2－2λ+1.

问题3  而点P实际上是动点，每当点P变化时，它与动点Q的最小距离都会随之变化，这个变化过程中，动点P与动点Q距离的最小值是多少？

当λ=23时，点P到直线A1C1的距离d取最小值33.

这样，以代数运算为依托，借助几何直观和空间想象感知运动过程中两点间距离的变化，体会运动变化中的对称美，在运算中深入理解空间中的两条直线异面这种位置关系.通过体会几何图形与代数运算间的紧密联系，感受代数与几何之间的和谐关系，发展学生几何直观素养、空间想象能力.直观想象也是探索、构建抽象结构的思维基础.

基于上述分析启发学生进一步思考：

问题4  直线AD1与直线A1C1是异面直线，要求两个动点P与Q间距离的最小值.是不是对于任意两条异面直线，都存在类似距离问题呢？你能结合图形说一说吗？

这个问题就是要启发学生再次展开空间想象、作图并深度思考.实质上就是考查两条异面直线间的距离的概念.什么是两条异面直线间的距离呢？这里可以利用高中数学知识结合几何图形来说明两异面直线之间存在公垂线段，且公垂线段唯一.

图5存在性：如图5，设l1，l2是異面直线，我们在l1上任取一点M，过点M作l′2∥l2，那么l′2与l1确定平面α.过l2向平面α作垂面γ，γ∩α=l，l∩l1=A，在面γ内过A向l2作垂线，垂足为B，易知AB⊥α，所以AB⊥l1且AB⊥l2.

唯一性：因为过l2向平面α所作垂面γ唯一确定，γ与α的交线l唯一确定，那么l与l1交点A也唯一确定，所以面γ内过A向l2作垂线得到的垂足B唯一确定.因此两异面直线之间的垂线段AB唯一确定.

通过上述分析，可知线段AB的长就是直线l2与平面α之间的距离，即：线l2到面α的距离就是公垂线段的长度.因此，直线l2上任意一点到平面α的距离就是两异面直线l1与l2间的距离.

于是有如下两个定义［5］：

定义1  两条直线上的点之间的最短距离称为这两条直线间的距离.

定义2  分别与两条异面直线垂直相交的直线称为两条直线的公垂线，两垂足的连线段称为公垂线段.

这样，引导学生聚焦重要数学概念、定理、方法、思想的理解和应用，强调基础性与综合性，注重对数学本质的认识，加强对通性通法的概括总结.

问题5  过l2也能作出与l1平行的平面β，记平面α与平面β间的距离d′，那么d′与公垂线段AB的长度有什么关系？

图6如图6，设l1，l2是异面直线，两异面直线l1与l2间的距离就是公垂线段AB的长.下面，我们在l1上任取一点M，过点M作l2′∥l2，那么l2′与l1确定平面α.在l2上任取一点N，过点N作l1′∥l1，那么l1′与l2确定平面β.那么两平面间的距离就是公垂线段的长度.也就是平面β上任意一点到平面α的距离就是两异面直线l1与l2间的距离.

基于以上分析可知，两异面直线间的距离既能转化为直线与平面间的距离，也能转化为两平行平面间的距离.

思路与方法3  借助点到平面的距离公式.

分析  在图4中，连接C1B，有AD1∥C1B，那么AD1∥面A1C1B，面A1C1B的一个法向量为n=（1，1，1），AA1=（0，0，1），点A到平面A1C1B的距离为d=AA1·nn=33.

与方法一和方法二相比较，方法三将异面直线间的距离转化为点到平面的距离，使得运算得到了简化.但其弊端也较明显，那就是：需要我们过其中一条直线A1C1作出与另一条直线AD1平行的平面A1C1B.

思路与方法4  求出两平行平面间的距离.

面ACD1∥面A1C1B，两平面三等分体对角线B1D，而B1D=3，所以两平行平面间的距离是33.

问题6  不画出平面α，能求出l2上任意点到平面的距离吗？你有什么办法？

实际上，我们并不需要作出上述平面A1C1B.在运算中，由于我们只需面A1C1B的法向量，而空间中向量是自由向量，所以只需求与两条异面直线的方向向量C1A1和AD1都垂直的向量，就是所需的面A1C1B的法向量.这样，不用做出平面，也可以利用点到平面的公式来求出异面直线间的距离.

问题7  在立体几何中，点到直线的距离和点到平面的距离都可以利用投影向量的模推出公式.我们能否也从投影向量的角度来思考两异面直线间的距离呢？

思路与方法5  巧用投影向量的模.

分析  如图7，l1，l2是两异面直线，n是l1，l2的公垂线段AB的方向向量.C，D分别是l1，l2上的任意两点，则CD在n上投影向量的模即为l1与l2之间的距离.

图7           图8

结合图8，具体运算过程如下：

AD1=（－1，0，1），A1C1=（－1，1，0），设n=（x，y，z），

令AD1·n=0，A1C1·n=0，即－x+z=0，－x+y=0，取n=（1，1，1）.

AA1=（0，0，1），则d=AA1·nn=33.

问题8  结合这个具体问题的解决过程，你能总结求异面直线间距离的具体步骤吗？

①在直线l1上取点A和C，在直线l2上取点B和D；

②通过AC和BD计算公垂线段的方向向量n；

③计算CD在n上的投影向量的模d=CD·nn.

3  拓展分析与教学启示

3.1  问题变式与拓展

图9如图9，在棱长为2的正方体ABCD-A1B1C1D1中，点M，N分别在线段AD1和B1C1上．给出下列四个结论：

①MN的最小值为2；

②有且仅有一条直线MN与AD1垂直；

③四面体NMBC的体积为83；

④存在点M，N，使△MBN为等边三角形．

其中所有正确结论的序号是    ．

一方面以面对角线和棱为背景，考查度量和位置关系；另一方面以正方体为依托讨论动线段相等的问题.突出对“灵活选择运用向量方法与综合几何方法”的考查.

3.2  教学启示

第一，试题设计要低起点以突出基础知识，问题设置要有层次以凸显知识联系.本题在正方体中，循序渐进地分析两动点在运动变化过程中，所对应线段长度的变化规律，体现了知识间的联系性，利于深入理解异面直线的位置关系，对于研究其它空间位置关系具有启发性.

第二，思路与方法的分析过程要具有微专题意识，求实、求透、求通.立体几何中常计算点到面的距离、线与面的距离、两平行平面间的距离，都可以用一个公式d=MN·nn，其中M与N两点分别在两个对象上，而n是平面的法向量.对于异面直线间的距离，也具有相通的方法，而n是与两异面直线的方向向量都垂直的向量.这体现了数学的整体性和统一美.

第三，反思要有整体意识，挖掘问题背后的本质和研究对象间的联系.本题中，引导学生建立形与数的联系，利用几何图形描述问题，借助几何直观理解问题，运用空间想象认识对象间的联系.帮助学生提升数形结合分析问题的能力，养成勤于反思的数学学习习惯，在立体几何这一具体的情境中感悟问题背后的本质.

参考文献

［1］  洪梦，吴立宝，王富英.数学说题的内涵与结构［J］.数学通报，2020，59（11）：58-63.

［2］  中华人民共和国教育部.普通高中数学课程标准：2017年版2020年修订［M］.北京，人民教育出版社，2020：29-42.

［3］  人民教育出版社  课程教材研究所  中学数学课程教材研究开发中心.普通高中教科书·数学·必修：第二册［M］.北京：人民教育出版社，2019：163-164.

［4］  人民教育出版社  课程教材研究所  中学数学课程教材研究开发中心.普通高中教科书·数学·选择性必修：第一册［M］.北京：人民教育出版社，2019：48-49.

［5］  丘维声.解析几何［M］.北京：北京大学出版社，1996：68-71.

作者简介  谷红霞（1984—）女，中学一级教师，曾获顺义区优秀教育工作者、朝阳区骨干教师、朝阳区骨干班主任等称号；荣获第八届高中青年数学教师优秀课展示与培训活动一等奖、北京市第二届京教杯青年教师教学基本功培训与展示活动一等奖、北京市示范性教研活动一等奖；主持并参与多项课题，发表文章10余篇.

谢辉（1974—）女，中学高级教师，任高中数学备课组长，朝阳区资源课程评审专家组成员；曾获朝阳区师德先進个人、朝阳区骨干教师、阳光杯班主任等称号；多次参与市、区级课程展示活动，参与朝阳区《高三目标检测》的编写.