永磁直线同步电机改进预测电流控制

摘"要：

永磁直线同步电机（PMLSM）预测电流控制（PCC）时存在易受参数变化和延迟以及负载扰动影响，为此提出基于二阶超螺旋滑模观测器（STSMO）的改进型PCC。首先，建立包含不确定性的PMLSM动态数学模型。然后，为了补偿参数变化以及延迟的影响，采用二阶STSMO估计下一周期的电流和参数变化造成的扰动电压，估计值用以计算下一周期的给定电压，以提高电流跟踪精确度，通过李雅普诺夫函数证明观测器的稳定性。同时，采用基于改进指数趋近律的自适应滑模控制器（ASMC）对速度进行跟踪，将状态变量和滑模面加入到指数趋近律中，不仅削弱了电流抖振，且进一步提升了系统的鲁棒性。半实物仿真实验结果表明，与传统PCC相比，提出方法能有效地抑制不确定性对系统影响，使系统具有更好的跟踪性能和鲁棒性。

关键词：永磁直线同步电机；预测电流控制；超螺旋滑模观测器；自适应滑模控制；鲁棒性

DOI：10.15938/j.emc.2024.01.008

中图分类号：TM351

文献标志码：A

文章编号：1007-449X（2024）01-0078-09

Improved predictive current control for permanent magnet linear synchronous motor

ZHAO Ximei，"YANG Mingdong，"JIN Hongyan

（School of Electric and Engineering， Shenyang University of Technology， Shenyang 110870， China）

Abstract：

Aiming at the problem that predictive current control （PCC） of permanent magnet linear synchronous motor （PMLSM） is susceptible to parameter change， delay and load disturbance， an improved PCC based on secondorder super twisting sliding mode observer （STSMO） was proposed. Firstly， a dynamic mathematical model of PMLSM with uncertainty was established. Then， in order to compensate for the influence of parameter change and delay， STSMO was used to estimate the current in the next cycle and the disturbance voltage caused by parameter changes. The estimated value was used to calculate the reference voltage in the next cycle to improve the current tracking accuracy， the stability of the observer was proved by Lyapunov function. At the same time， the adaptive sliding mode controller （ASMC） based on the improved exponential reaching law was used to track the speed. By adding the state variables and sliding mode surface to the exponential reaching law， the current chattering is not only weakened， but also the robustness of the system is further improved. The results of hardware in the loop simulation experiment show that， compared with traditional PCC， the proposed method can effectively suppress the influence of uncertainty on the system， and make the system have better tracking performance and robustness.

Keywords：permanent magnet linear synchronous motor; predictive current control; supertwisting sliding mode observer; adaptive sliding mode control; robustness

0"引"言

永磁直线同步电机（permanent magnet linear synchronous motor，PMLSM）因具有动态响应快、高效率、高推力密度等优点而广泛应用于各种高端制造装备中[1]。电流内环作为连接电机运动单元和控制单元的枢纽，在电机控制中起着关键作用，电流内环的性能直接影响着外环的性能，性能优良的电流控制方法在电机控制中起着至关重要的作用。

预测电流控制（predictive current control，PCC）因其高带宽、高跟踪精确度、能够解除耦合关系等优点而引起了广泛关注[2-4]。采用PCC时，实际电流可以在一个开关周期内精确跟踪给定电流。因此，PCC非常适合应用于高性能的电机控制[5]。然而，延迟和参数变化2个问题会严重影响PCC的性能。

为了解决延迟问题，文献[6]采用硬件设计技术实现预测控制，但是基于硬件语言的编程方法不便于开发算法，具有大量的工程工作。文献[7]通过估算下一采样周期给定电压可以解决延迟问题，但该方法忽略了电机参数变化对控制方法的影响。文献[8]设计了1.5拍相角补偿环节，仅可抵消延迟模型的复常数部分，不能完全抵消延时影响。为了解决参数变化问题，文献[9]采用时延控制技术补偿参数扰动，然而由于这种方法在对电流进行微分计算时带来大量噪声，需要进行复杂的滤波器设计。文献[10]设计了离散的扩张状态观测器（extended state observer，ESO）来估计系统扰动，此方法降低了对电机模型参数的依赖，但参数估计精确度受到制约。文献[11]设计了变增益龙伯格观测器，虽能消除模型参数不准确带来的电流静差，但需要调节的参数较多。

滑模观测器（sliding mode observer，SMO）对外界干扰鲁棒性强，但存在抖振和观测精确度低等问题[12]。文献[13]将二阶滑模算法代替传统开关函数从而抑制转速抖振，但未对观测器进行稳定性分析。文献[14]针对观测器对参数变化鲁棒性差的问题研究了一种自适应滑模观测器实现对转速与磁链的估计，但所用开关函数会增大抖振，系统未知参数过多且难以调节。滑模控制（sliding mode control，SMC）虽然响应快、鲁棒性强，但也存在抖振问题。对此，文献[15]提出一种自适应滑模控制对抖振进行抑制，但该系统控制结构单一，且当电机受到外部扰动时，电机会出现一定的超调和抖振。

基于上述分析，本文提出基于二阶超螺旋滑模观测器（super twisting sliding mode observer，STSMO）的改进型PCC与自适应滑模控制器（adaptive sliding mode controller，ASMC）相结合的控制方法，应用于PMLSM伺服系统中，确保高精确度的电流跟踪。改进PCC作为内环，确保了电流环响应的快速性，同时以二阶STSMO估计下一周期参数变化造成的扰动电压和下一周期电流，抑制参数变化和延迟带来的影响；ASMC通过将状态变量和滑模面加入到改进指数趋近律中，削弱电流的抖振，提高系统鲁棒性。最后通过半实物仿真实验验证方法的有效性。

1"PMLSM数学模型

PMLSM的电压方程可以表示为：

其中m为电机质量。

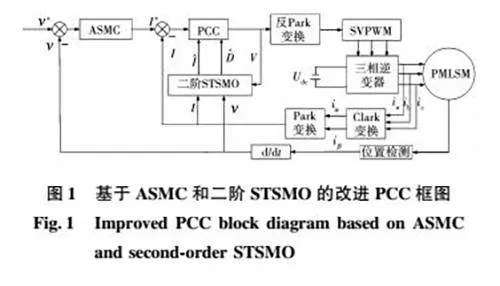
针对上述的不确定性，为确保实际速度跟踪给定速度，本文设计了基于二阶STSMO的改进型PCC和ASMC相结合的控制方法。系统框图如图1所示。

1.1"延迟问题分析与改进

根据式（1）的电压方程，其离散时间方程可以表示为一阶泰勒级数的形式，如果采样周期足够短，则表示为：

其中矩阵G和H是由电机电阻、电感、极距和速度等决定的矩阵。

便于后续分析，将式（9）中第（k+1）个周期开始时的电流矢量移到等式左侧，可以表示为

若不考虑数字控制的延迟，给定电压V*（k）根据式（9）推导出：

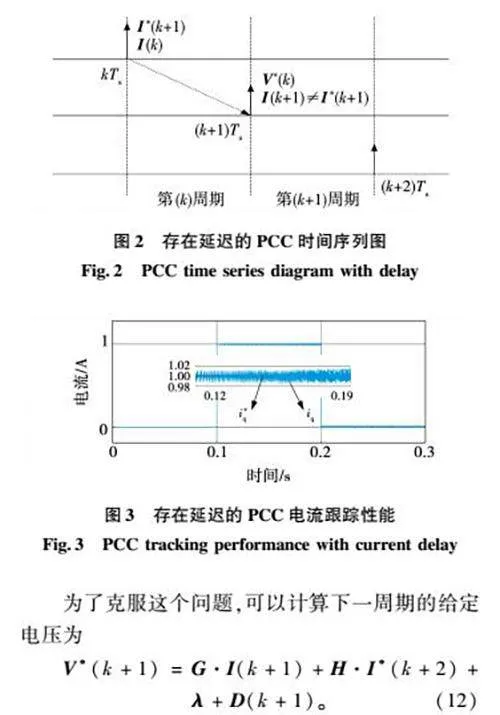
如果忽略扰动D（k），理论上实际电流可以在一个采样周期后跟踪上给定电流。然而，由于数字控制中的一步延迟，V*（k）在一个周期后才施加到逆变器上。因此，实际电流的稳定性较差。存在延迟问题的PCC时序图和电流跟踪效果如图2和图3所示。

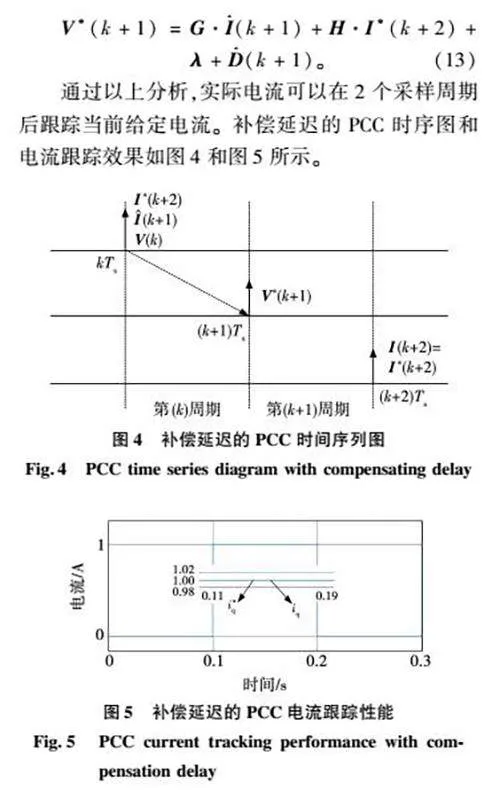
通过以上分析，实际电流可以在2个采样周期后跟踪当前给定电流。补偿延迟的PCC时序图和电流跟踪效果如图4和图5所示。

1.2"参数敏感性分析

在理想情况下，实际电压等于给定电压，即V*（k+1）=V（k+1），由式（9）可知，V（k+1）满足下面关系：

当电阻发生变化（扰动值为ΔR），其他参数不变时，根据式（3）和式（16），将跟踪误差简化为：

由式（17）可知，电流达到稳态后存在恒定误差，且与扰动值ΔR成正比。

当电感发生变化（扰动值为ΔL），其余参数不变，则误差表示为：

从式（18）等式右侧可以看出，第一项与实际电流有关，即电感的变化会影响电流控制器的动态特性。此外，第二项的值与速度和d轴或q轴电流成正比。由于本文采用id=0的磁场定向控制方法，所以第二项主要带来d轴电流跟踪误差。

当只有磁链变化（扰动值为Δλf）时，误差为：

由式（19）得，d轴电流不受磁链变化的影响，但q轴电流的跟踪误差随实际速度的变化而变化，误差与速度成正比。

2"二阶超螺旋滑模观测器

2.1"观测器设计

根据上节的分析，I（k+1）和D（k+1）的准确估计在获得高性能PCC中起着至关重要的作用。因此，本节通过设计二阶STSMO估计I（k+1）和D（k+1）。

以q轴电流iq为例设计观测器，根据式（10）考虑参数变化时，状态方程为：

3"自适应滑模控制器

本文在传统的指数趋近律滑模控制器上进行改进，提出一种新的自适应指数趋近律：

其中：K＞0；δ＞0；0＜ε＜1；K1＞0；0＜b＜1；s为滑模面。

由式（41）可知，当s增大时，第一项趋近于K/ε，K/ε大于传统指数趋近律中的K，第二项趋近于K1|s|bs；当s减小时，第一项趋近于K|x|/（1+|x|），其中|x|随着系统逐渐稳定而减小到0，这意味当系统轨迹接近滑模面时，变量M逐渐减小到0，第二项逐渐收敛到K1，2个参数逐渐变化，不仅增加了控制器的鲁棒性而且削弱了抖振。

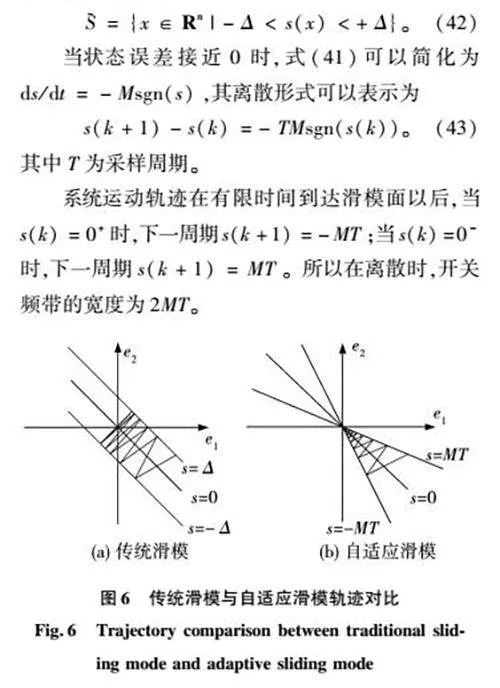
SMC在实际的数字离散系统中，与连续系统有着较大区别，其轨迹如图6所示。从离散的角度比较了改进趋近律与传统指数趋近律。围绕滑模面的开关频带可以表示为

当状态误差接近0时，式（41）可以简化为ds/dt=－Msgn（s），其离散形式可以表示为

其中T为采样周期。

系统运动轨迹在有限时间到达滑模面以后，当s（k）=0+时，下一周期s（k+1）=－MT；当s（k）=0－时，下一周期s（k+1）=MT。所以在离散时，开关频带的宽度为2MT。

如图6所示，在从初始状态到滑模面的整个过程中，新趋近律不仅速度更快而且削弱了抖振。

4"仿真实验结果

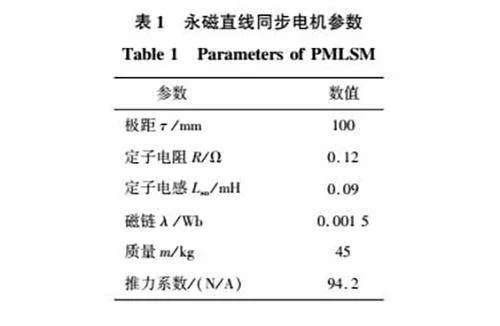
为了进一步验证所提出的控制方法的有效性，对其进行仿真实验分析。实验平台主要包括伺服驱动器、运动控制试验箱、上位机和PMLSM，如图7所示。仿真实验中采用的电机参数如表1所示。

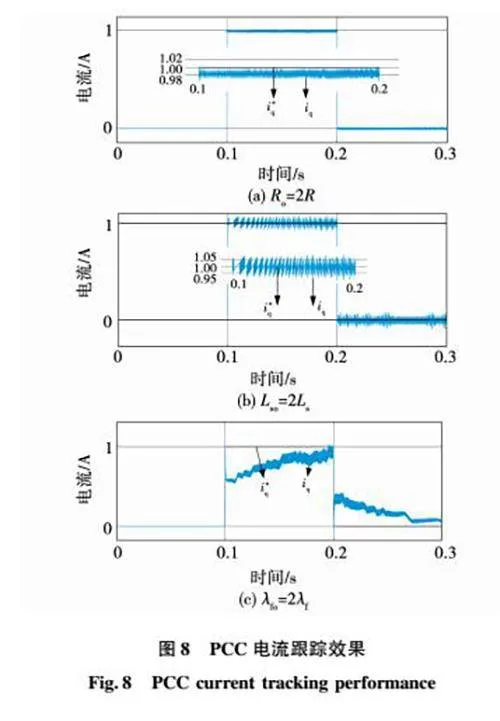
传统PCC在参数匹配时具有优良的静动态性能，如图5所示。但在电机参数变化时会对系统稳定性造成较大的误差，而且不同的参数变化会对电流跟踪性能造成不同的影响，如图8所示。

由图8可知，当电阻变化时，电流会存在稳态误差，低于给定电流0.02 A；当电感变化时，电流以0.1 A的幅值在给定电流附近振荡；当磁链变化时，电流误差与实际速度有关。与参数匹配时（图5）相比，电流跟踪性能显著下降。

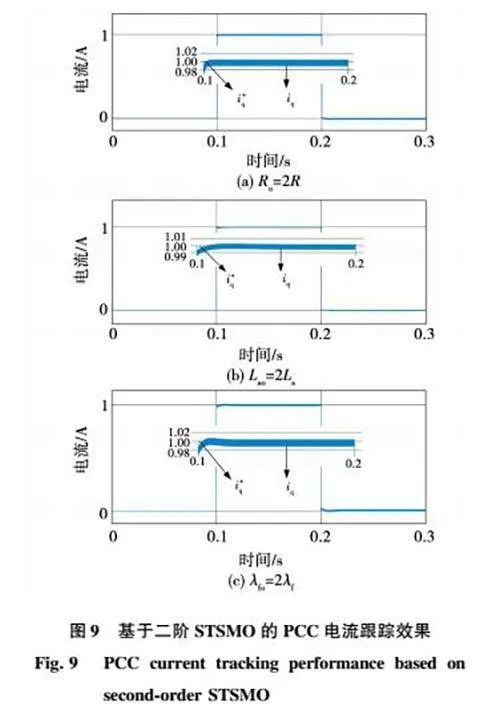
将二阶STSMO参数设置为k1=1 500、k2=2 500，电流跟踪效果如图9所示。

由图9可知，引入观测器后与无观测器相比，在电阻变化时，电流稳态误差降低0.01 A；在电感变化时，振荡幅值降低了0.045 A，电流由与速度有关变为精确跟踪给定电流，有效提高了电流跟踪精确度。在保证PCC优良静动态性能的同时，有效地提高了电流的跟踪精确度。

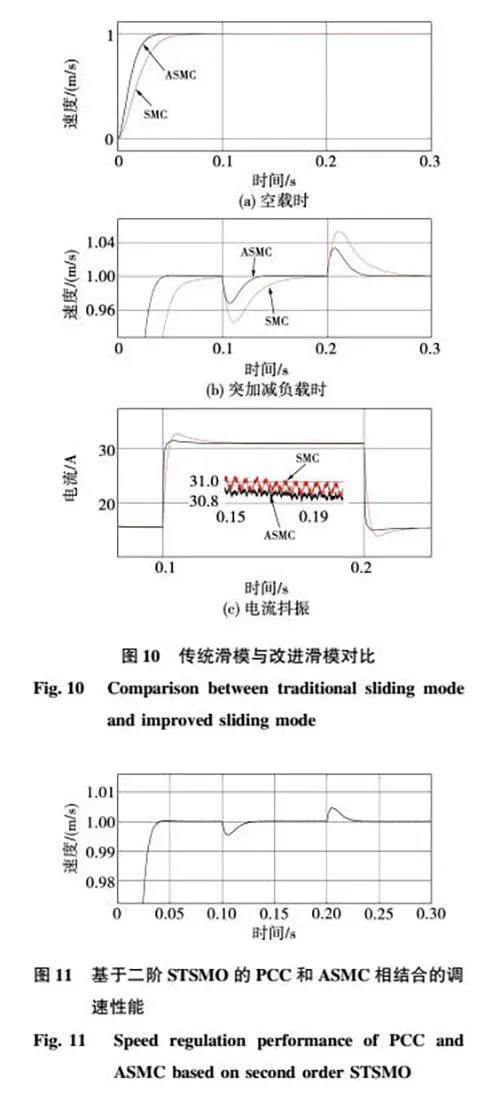
ASMC参数取K=50、ε=0.1、δ=2、K1=350、b=0.01，空载时和0.1 s、0.2 s分别对电机突加200 N负载和突减200 N负载，传统SMC和改进的ASMC调速效果如图10所示。

图10中，改进ASMC与传统SMC相比，到达稳态的时间快了约0.04 s。突加负载后改进型ASMC比传统SMC速度下降0.03 m/s。改进型ASMC比传统SMC电流抖振幅值低0.05 A。通过将状态误差和滑模面引入指数趋近律系数中，不仅改善了系统的响应速度和抗扰能力而且削弱了电流的抖振。引入二阶STSMO和ASMC后，在0.1 s和0.2 s分别对电机突加和突减200N负载，电机的调速性能如图11所示。

由图11可知，所提出的控制方法具有优良的静动态性能，与改进ASMC相比，到达稳态的时间降低约0.02 s，突加负载时，速度下降低于改进ASMC约0.005 m/s。表明该方法有效提高了系统的鲁棒性和跟踪性。

5"结"论

针对传统PCC存在延迟和易受参数变化影响等问题，本文通过提前计算下一周期给定电压和引入二阶STSMO估计下一周期参数变化造成的扰动电压和电流，在保证PCC优良静动态性能的同时，提高了PCC的电流跟踪精确度和鲁棒性。为进一步提高改进PCC下PMLSM系统的调速性能，设计了ASMC，通过在趋近律系数中加入状态误差和在指数项中加入滑模面，不仅削弱了电流抖振，而且增加了电流的跟踪精确度和系统的抗扰性能。半实物仿真实验结果验证了所提出控制方法的有效性。

参 考 文 献：

［1］"王明义.精密永磁直线同步电机电流闭环控制关键技术研究[D].哈尔滨： 哈尔滨工业大学，2016.

［2］"SUN Xiaodong， CAO Junhao. A robust deadbeat predictive controller with delay compensation based on composite slidingmode observer for PMSM[J]. IEEE Transactions on Industrial Electronics，2021，36（9）：10742.

［3］"JIANG Yajie， WEI Xu， CHAO Xumu. Improved deadbeat predictive current control combined sliding mode strategy for PMSM drive system[J]. IEEE Transactions on Vehicular Technology，2018，67（1）：251.

［4］"WANG Bo， ZHEN Dong， YU Yong. Static errorless deadbeat predictive current control using secondorder slidingmode disturbance observer for induction machine drives[J]. IEEE Transactions on Power Electronics，2018，33（3）：2395.

［5］"卜飞飞，罗捷，刘皓喆，等.双绕组感应发电机系统无差拍电流预测[J].电工技术学报，2021，36（24）：5213.

BU Feifei， LUO Jie， LIU Haozhe， et al. Deadbeat predictive current control strategy of dual winding induction generator system[J]. Transactions of China Electrotechnical Society，2021，36（24）：5213.

［6］"TU Wencong， LUO Guangzhao， CHEN Zhe. FPGA implementation of predictive cascaded speed and current control of PMSM drives with twotimescale optimization[J]. IEEE Transactions on Industrial Informatics，2019，15（9）：5276.

［7］"ZHANG Xiahe， HUANG Xiaoyan. An incremental deadbeat predictive current control method for PMSM with low sensitivity to parameter variation[C]//2020 International Conference on Electrical Machine， August 23-26，2020， Gothenburg， Sweden. 2020： 1060-1066.

［8］"国敬，范涛，章回炫，等.高速低载波比下永磁同步电机电流环稳定性分析[J].中国电机工程学报，2019，39（24）：7336.

GUO Jing， FAN Tao， ZAHNG Huixuan， et al. Stability analysis of permanent magnet synchronous motor current loop control at high speed and low carrier ratio[J]. Proceedings of the CSEE，2019，39（24）：7336.

［9］"GAO Jinqiu， GONG Chao， LI Wenzhen， et al. Novel compensation strategy for calculation delay of finite control set model predictive current control in PMSM[J]. IEEE Transactions on Industrial Electronics，2020，76（7）：5816.

［10］"KE Dongliang， WANG Fengxiang， HE Long. Predictive current control for PMSM system using extended sliding mode observer with hurwitzbased power reaching law[J]. IEEE Transactions on Power Electronics，2021，36（6）：7223.

［11］"YAN Liming， WANG Fengxiang， RODRIGUEZ J. Luenberger prediction modelbased robust predictive current control of induction machine drives[C]//2020 IEEE 9th International Power Electronics and Motion Control Conference， November 28-30， 2020， Nanjing， China. 2020： 1006-1010.

［12］"孙宜标，仲原，刘春芳.基于LMI的直线伺服滑模位移跟踪控制[J].电工技术学报，2019，34（1）：33.

SUN Yibiao， ZHONG Yuan， LIU Chunfang. LMIbased sliding mode displacement tracking control for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society，2019，34（1）：33.

［13］"OLIVEIRA C M R， AGUIAR M L， MONTEIRO J R B A，et al. Vector control of induction motor using an integral sliding mode controller with antiwindup[J]. Journal of Control Automation and Electrical Systems，2016，27（21）：169.

［14］"高艳霞，陈静，范应鹏，等 .一种用于异步电机无速度传感器控制的自适应滑模观测器[J]. 电机与控制学报， 2017，21（4）：8.

GAO Yanxia， CHEN Jing， FAN Yingpeng， et al. An adaptive sliding mode observer based sensorless control of induction motors[J]. Electric Machines and Control， 2017，21（4）：8.

［15］"LENG Jianwei， MA Chang. Sliding mode control for PMSM based on a novel hybrid reaching law[C]//2018 37th Chinese Control Conference （CCC）， July 25-27，2018， Wuhan， China. 2018： 3006-3011.

（编辑：邱赫男）

收稿日期： 2022-06-16

基金项目：辽宁省自然科学基金计划项目（2022-BS-177）

作者简介：赵希梅（1979—），女，博士，教授，研究方向为直线伺服、数控、鲁棒控制等；

杨名冬（1996—），男，硕士研究生，研究方向为直线电机及其控制；

金鸿雁（1993—），女，博士，讲师，研究方向为电机控制、鲁棒控制等。

通信作者：赵希梅