温度影响下的开槽盘式磁力耦合器调速特性

摘"要：

针对温度影响下盘式磁力耦合器调速问题，以一台6对极16槽的开槽盘式磁力耦合器为研究对象，基于矢量磁位法，结合修正三维端部效应的卡特系数并考虑温度对永磁体剩磁的影响，依据磁力耦合器轴向介质不同与导体盘轭铁和铜导体交替排列的结构， 推导出其整体的电磁转矩公式。再分别建立恒转矩负载、二次方率负载和恒功率负载工况下的调速关系解析模型。通过有限元模拟分析，确定了不同温度、不同气隙下的开槽盘式磁力耦合器在3种不同负载工况下的调速范围与调速特性。最后，搭建试验平台进行调速性能试验，将不同负载工况下磁力耦合器电磁转矩与输出转速的理论、仿真、实验值三者进行对比，结果表明理论模型有较高的准确性，为开槽型磁力耦合器在调速系统中的智能调控提供了理论依据。

关键词：盘式磁力耦合器；开槽型；矢量磁位；温升影响；电磁转矩；调速性能

DOI：10.15938/j.emc.2024.01.007

中图分类号：TH133.4

文献标志码：A

文章编号：1007-449X（2024）01-0069-09

Speed regulation performance of slottedtype axialflux magnetic couplers under temperature influence

YANG Chaojun，"QI Yutang，"DING Yifei，"ZHANG Yiwen

（School of Mechanical Engineering， Jiangsu University， Zhenjiang 212013， China）

Abstract：

In order to solve the speed regulation problem of the axialflux magnetic coupler affected by temperature， a slottedtype magnetic coupler with 6 pairs of poles and 16 slots was taken as the research object. Based on the axial media of the magnetic coupler and the structure of the conductor disk yoke with alternating arrangement of iron and copper conductors， using the vector magnetic potential method， combined with the Carter coefficient of correcting the threedimensional end effect，taking the influence of temperature on the remanence of permanent magnets into consideration， the whole electromagnetic torque formula was derived. Then， the analytical models of speed regulation relationship under constant torque load， quadratic rate load and constant power load were established respectively. By using finite element simulation， the speed range and characteristics of the slottedtype magnetic coupler under different temperature and air gap were determined under three different load conditions. Finally， a test platform was built for speed regulation performance test， and the theoretical， simulation and experimental values of electromagnetic torque and output speed of magnetic coupler under different load conditions were compared. It is found that the theoretical model has high accuracy， and these studies provide a theoretical basis for intelligent control of slotted magnetic coupler in speed control system.

Keywords：axialflux magnetic coupler; slottedtype; vector magnetic potential; influence of temperature rise; electromagnetic torque; speed regulation performance

0"引"言

磁力耦合器是一种由电磁力驱动，主从动盘无需机械连接的传动装置，相对于传统的机械连接方式，其具有节能环保、软启动、耐腐蚀、无谐波污染等多种优势，因此在农业、矿业、船舶业等都有着较为广泛的应用[1-5]。

由于磁力耦合器的诸多优点和广泛应用，许多国内外学者进行了相关研究。2015年KyoungChul Min等[6]运用二维极坐标下的矢量磁位法，研究了不同充磁角度下的双层Halbach磁力耦合器，通过分析其涡流损耗情况，为Halbach型磁力耦合器的设计提供了理论依据。2017年Thierry Lubin等[7]运用了三维极坐标下的标量磁位法，对盘式磁力耦合器的机械特性及导体盘温度对输出转矩的影响进行了研究， 通过有限元及理论计算结果的对比分析，验证了该理论，有效地简化磁力耦合器参数设计及优化。2016年上海交通大学的代欣[8]运用了柱坐标系下的矢量磁位法分析了开槽盘式磁力耦合器，通过在铜导体盘的轭齿及铜导体的边界上添加沿周向的边界条件，使得理论与仿真结果得到了较高的一致性。2021年，江苏大学杨超君等[9]针对盘式异步磁力耦合器的转速调控问题，建立磁路计算模型，推导出电磁转矩公式，分别建立恒转矩负载、二次方率负载和恒功率负载工况下的调速关系解析模型，并结合有限元仿真及实验进行了验证。但上述文献对磁力耦合器的研究通常忽略了永磁体在温升后磁性下降的影响，实际上因工作温度上升，永磁体磁性下降对耦合器转矩的削弱是不可避免的，研究永磁体温升的影响对实际生产有着较大的指导作用。

本文以6对极开槽盘式磁力耦合器为研究对象，通过二维矢量磁位法并结合温度对永磁体性能影响的关系式，推导考虑导体盘轭铁的电磁转矩表达式。并建立恒转矩负载、二次方率负载和恒功率负载工况下的计算模型，再通过有限元模拟得到不同温度、不同负载工况下磁力耦合器的调速范围，最后通过实验验证理论模型的准确性。

1"电磁转矩及调速关系

1.1"开槽盘式磁力耦合器结构与调速机理

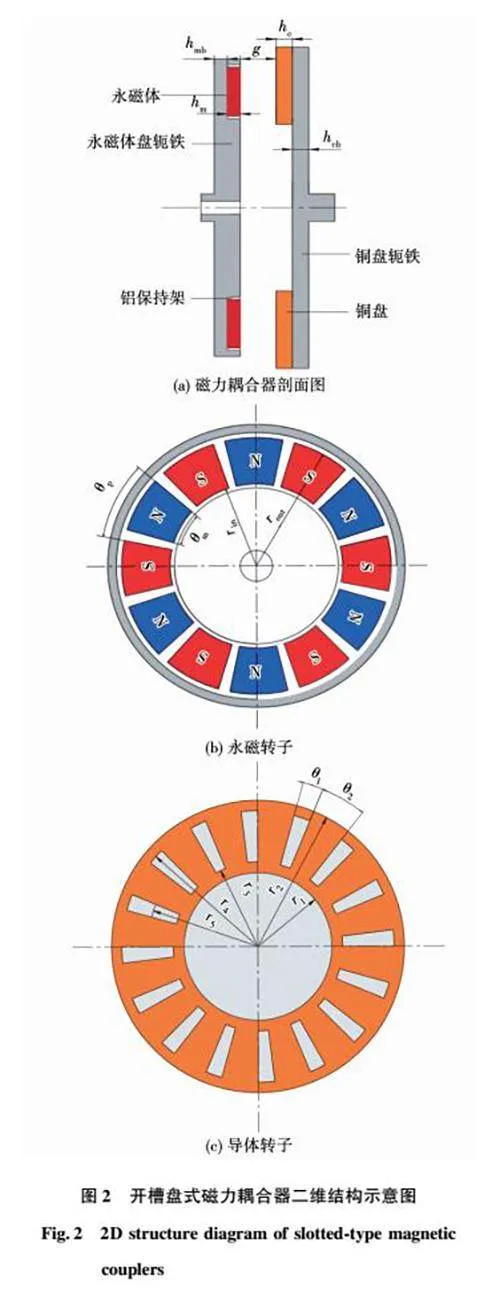
图1为开槽盘式磁力耦合器的三维结构示意图，其由永磁体、铝合金保持架、永磁体轭铁盘、铜导体盘、铜导体轭铁盘5部分组成，永磁体嵌于铝合金保持架中并整体包络在永磁体轭铁内构成永磁转子，铜导体盘上开槽并与铜导体轭铁盘上的轭齿相结合构成导体转子。图2为该耦合器的二维结构示意图，永磁转子沿周向N、S极永磁体交替排布，相邻磁极由铝合金保持架隔开，导体转子沿周向铜导体及轭齿交替排布，两转子轴向由气隙隔开。

图3为开槽盘式磁力耦合器工作原理图，其工作原理为[10-11]：主动转子由电机拖动，相对从动转子形成转速差，磁场磁力线由永磁体垂直穿入导体转子内，基于电磁感应原理在导体盘中形成感应电流进而产生电磁转矩。

通过调整气隙厚度可以对输出转速及输出转矩进行无级调节，当主动转子与从动转子靠近而之间的气隙变小时，铜盘由于切割磁力线增加而使气隙磁密随之增加，相应的磁力耦合器所传递的转矩增大，导致无法实现输出转矩与负载转矩的平衡，这时就需要降低转差率来提高输出转速以降低输出转矩，进而达到转矩的平衡。当主动转子与从动转子远离而之间的气隙变大时，则情况相反。另外，在温度升高的影响下，输出转矩也会有所降低，故研究温度影响下磁力耦合器的调速特性是有必要的。磁力耦合器的相关参数见表1和表2。

1.2"理论推导

为简化理论分析模型，依据磁力耦合器平均半径处沿周向展开为二维层分析模型。运用矢量磁位法进行求解时，忽略磁力耦合器导体盘轭齿聚磁性所产生的影响，仅依据轴向介质不同设立边界方程。通过对1、3、5次谐波求和计算轴向磁通密度及电磁转矩[12-14]。为便于计算，同时保证理论的准确性做出如下假设：

1）耦合器的气隙磁场仅由永磁体产生，忽略铜导体内感应涡流形成的感应磁场对原磁场的削弱作用。

2）耦合器内的永磁体沿轴向充磁且各区域介质为线性介质，不随外部条件改变而改变。

3）耦合器内各导磁材料无磁饱和效应。

图4为开槽盘式磁力耦合器的二维层分析模型图，其中原点设在某一铜导体区的右下角，x轴指向导体盘周向方向，y轴指向导体盘轴向方向，z轴指向导体盘径向方向。除永磁体轭铁盘及铜盘轭铁盘外的真空区外，依据轴向介质的不同将耦合器划分为区域1～区域5，藉此沿轴向区域划分可得到边界1～边界6，进而设立边界方程并求解矢量磁位[15-18]。其中区域2沿周向可分为轭齿区及铜导体区，区域4沿周向可分为永磁体区及铝合金保持架区。

在任一磁场空间中的磁感应强度可表示为[15]

式中：αBr为永磁体的剩磁温度系数，钕铁硼材料系数为-0.126%℃k-1；Br0为永磁体在常温下的剩磁；t为永磁体温度；t0为室温。

依据各区域中磁化强度与感应电流的存在情况，结合式（17）得到各区域的矢量磁位方程。再依据二维层模型除气隙外的各区域的分界面，即边界2～边界5处磁通密度满足法向分量连续，磁场强度满足切向分量连续，边界1及边界6满足轴向磁场强度为0，则可确定边界条件[20]：

式中：A～1zn为区域1轭铁的矢量磁位复振幅；A～2zn（Cu）为区域2铜导体的矢量磁位复振幅；A～2zn（cog）为区域2轭齿的矢量磁位复振幅；A～3zn为区域3气隙的矢量磁位复振幅；A～4zn为区域4永磁体的矢量磁位复振幅；A～5zn为区域5轭铁的矢量磁位复振幅；μyoke为轭铁磁导率；σyoke为轭铁的电导率；σCu为铜的电导率；μ4x为永磁体等效磁导率；μ4r为永磁体相对磁导率。

运用MATLAB求解则可求出各区域的矢量磁位。本文研究的磁力耦合器导体转子为16开槽鼠笼盘，永磁转子为6对极永磁体，由于转矩来源于铜导体及其轭铁两部分，依据导体转子沿轴向轭齿区与铜导体区交替排布的性质，可以将电磁转矩分为两部分计算。

1）对于单个轭齿区所对应的轴向区域产生的电磁转矩为

式中：q∈[1，2，…，k]为耦合器二维展开模型中从左至右第q个轭齿；θ1为轭齿区对应的圆周角度；θ2为铜导体区对应的圆周角度；wcog为轭齿的径向厚度；y1为边界1处的纵坐标值；y3为边界3处的纵坐标值。

由此，所有轭齿区所对应的轴向区域产生的电磁转矩为

2）对于单个导体区所对应的轴向区域产生的电磁转矩为

故所有铜导体区所对应的轴向区域产生的电磁转矩为

2"调速特性仿真分析

2.1"有限元模型建立

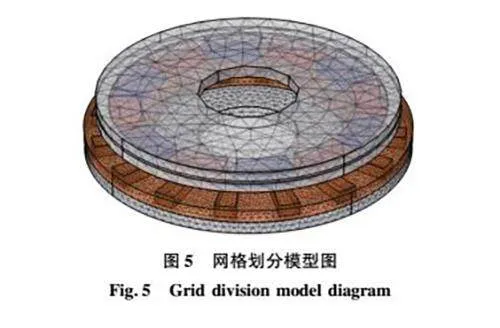
为了得到开槽盘式磁力耦合器的电磁转矩及调速关系的数学模型，在有限元软件的电磁学模块中建立三维模型，其中永磁体为6对极且沿轴向充磁，其相关材料及结构参数如表1与表2所示。模型建立后，对其进行网格划分及求解设置，如图5所示。

2.2"调速特性仿真分析

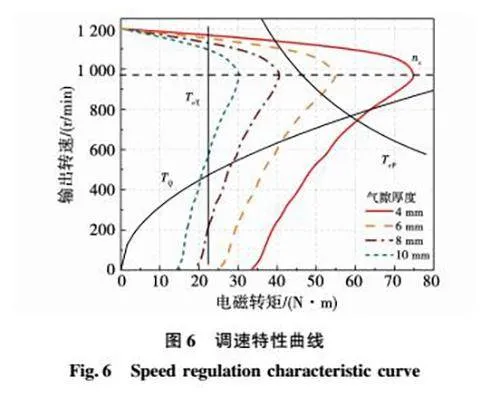
将式（33）～式（35）中负载转矩方程所对应的函数曲线结合仿真所得的机械特性曲线可得到如图6所示的调速特性图，其中nc为磁力耦合器最大输出转矩时的输出转速，即临界转速，依照n=nc可将该图分为上下两部分。n=nc以下为启动过程，n=nc以上为稳定运行过程，且负载转矩曲线与机械特性曲线的交点为该负载工况下的稳定运行点。

为使耦合器能够稳定运行，需满足机械特性曲线的斜率小于负载曲线在该点的斜率，故进行恒转矩与恒功率负载调速范围分析时，仅取n=nc以上部分；而进行二次方率负载调速分析时，则可取全部的调速范围。将耦合器在3种负载下所能取得最大调速范围的值称为临界转矩（Tc）、临界系数（kc）与临界功率（Pc），则Tc、Pc分别为耦合器大气隙取临界转速时的输出转矩与输出功率，kc为耦合器小气隙取临界转速时的二次方率系数，类似地将耦合器在调速范围内可取得的最大值称为最大转矩（Tmax）与最大功率（Pmax）。

为研究永磁体温度上升对耦合器性能的影响，结合式（15）及式（16）与表1中相关永磁体温度参数可得到不同温度下耦合器的调速范围。由于在磁力耦合器实际应用中，一方面出于安全因素和制造与安装要求，气隙厚度不宜过小，且当气隙厚度过大时输出转矩过小无实际应用价值。另一方面当永磁体温度高于最高工作温度时会急剧退磁，故做出以下两点假设：

1）磁力耦合器的工作气隙厚度为4～10 mm；

2）磁力耦合器的最高工作温度为100 ℃，且在该工作温度内，永磁体均匀退磁。

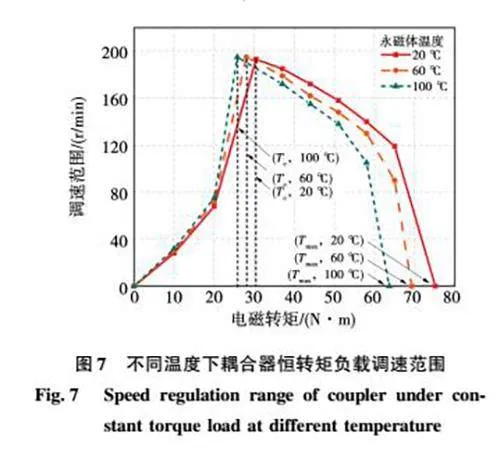
2.2.1"恒转矩负载下的调速性能分析

以调速特性的外侧曲线为基准，可得到不同温度时恒转矩负载下耦合器的调速范围曲线如图7所示。可知，随着温度的增加，永磁体磁性下降，但磁力耦合器的调速范围变化均呈现先变大后逐渐变小的趋势，且下降区间约为上升区间的两倍。由于温度的升高，耦合器所能承载的恒转矩负载范围由75.14 N·m下降至63.65 N·m，且在相同的转速差下耦合器的转矩逐渐下降，故而耦合器的调速范围曲线呈现近似整体偏移的趋势。但不同温度下磁力耦合器最大调速范围近似不变，约为0～195 r/min。此外在临界转矩与最大转矩附近，相同的温度差下，随着温度的升高，耦合器调速范围的差值随着恒转矩负载的增大而增大。由此可知，随着工作转矩逐渐逼近临界转矩与最大转矩，永磁体温升对耦合器的调速范围影响越来越大。

2.2.2"二次方率负载下的调速性能分析

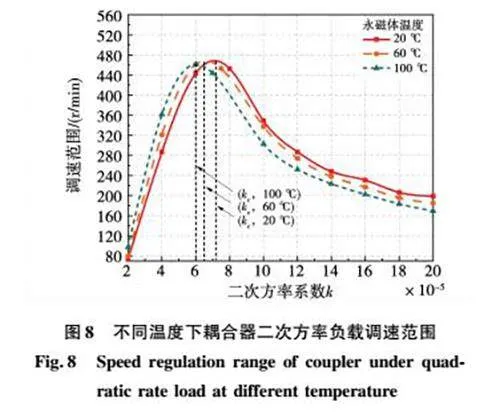
图8为不同温度时二次方率负载下耦合器的调速范围曲线，不同温度时二次方率负载下的调速曲线均呈现先迅速增大后缓慢减小的趋势。不同温度下临界系数kc不同，且温度越高，该系数越小。当永磁体温度由20 ℃上升至100 ℃时，临界系数则从7×10-5下降至6×10-5附近。当二次方率系数小于临界系数时，温度越高则调速范围越大，反之则调速范围越小，且在临界系数附近时，温度对调速范围的影响越大。此外，当二次方率系数大到一定值时，继续增大系数对耦合器的调速范围影响较小。

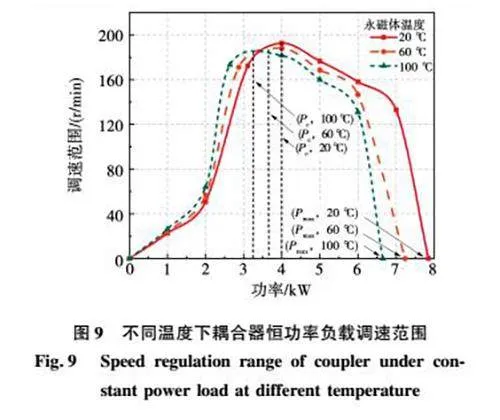
2.2.3"恒功率负载下的调速性能分析

图9为不同温度时二次方率负载下耦合器的调速范围曲线，在恒功率负载下，不同永磁体温度的耦合器调速曲线近似相同，随着永磁体的温度从20 ℃上升至100 ℃，恒功率负载下耦合器的最大调速范围从0～193 r/min下降至0～180 r/min。此外，温度越高，则耦合器的临界功率越低。据此可近似认为，在小于临界功率时，温度越高调速范围越大；而大于临界功率时，温度越低则调速范围越大。进一步观察可知，当耦合器的功率靠近临界点与最大点时，耦合器调速范围的变化越大。

3"实验验证

3.1"试验装置

图10为磁力耦合器实验平台，其主要由控制平台和实验平台构成，控制平台可通过PID对实验平台远程控制，设定输入转速为1 200 r/min，气隙厚度为4～10 mm，调节转速差、输入转矩等值，并可实时接收数据反馈。实验平台由三相异步驱动电机、三相异步负载电机、导体转子、永磁体转子及转速转矩传感器组成。

3.2"实验结果及分析

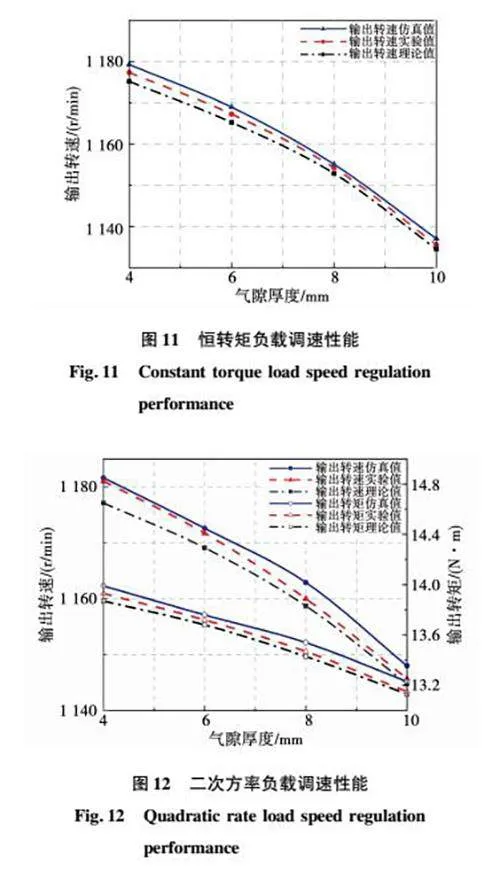
图11为恒转矩负载15 N·m时输出转速随气隙变化的曲线。实验中，当气隙厚度由4 mm增加到10 mm时，输入转速一定时，输出转速由1 177.3 r/min下降至1 135.5 r/min。此外，随着气隙厚度的增大，当气隙厚度的增量一定时，若要达到相同的输出转矩，则需要的转速差增量越大，且当恒转矩负载较小时，仿真、实验、理论值三者之间误差较小。

图12为输出转速与输出转矩随气隙变化的曲线。当输入转速一定时，当气隙厚度由4 mm增加到10 mm时，仿真、实验、理论值三者的变化趋势近似一致，输出转速与输出转矩皆近似呈线性变化，输出转速的降幅为35.7 r/min，输出转矩的降幅为0.78 N·m，可见相同二次方率系数下，随着气隙厚度的增加，输出转速较输出转矩的降幅更大，且实测的二次方率系数均在目标系数较小范围内上下波动。可见在二次方率负载系数较小时，理论计算的结果较为准确。

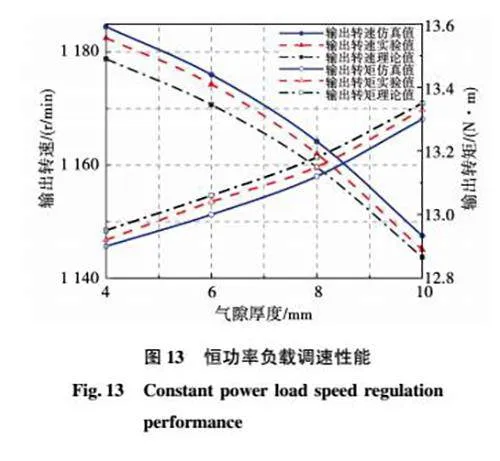
图13为输出转速与输出转矩随气隙变化的曲线。当输入转速保持1 200 r/min，气隙厚度由4 mm增加到10 mm时，输出转速由1 184.1 r/min下降至1 145.2 r/min，与二次方率负载不同，随着气隙厚度的增大，输出转矩由12.92 N·m上升至13.33 N·m。由此，耦合器在恒功率负载下且功率较小时，输出转速较输出转矩受气隙厚度影响更大。该理论在恒功率负载较小的情况适用性较好。

4"结"论

1）通过将开槽盘式磁力耦合器沿周向展开建立二维层分析模型，考虑了温度对永磁体剩磁变化的影响，依据磁力耦合器轴向介质不同与导体盘轭铁和铜导体交替排列的结构，推导出其整体的转矩公式。

2）在正常工作温度范围内，永磁体温度升高对耦合器调速曲线的临界值和最大值附近影响最大；恒转矩、恒功率、二次方率负载下耦合器的调速特性曲线中，调速范围均呈现先变大后减小，其中恒转矩与恒功率负载的调速曲线较为相似，二次方率负载所能取得的调速范围最大，且调速范围随系数的变大其调速范围逐渐平稳。

3）在实际应用实践中，温度对磁力耦合器性能的影响是由导体盘和永磁体盘复合作用导致的复杂情况，为简化分析，本文仅考虑温度对永磁体磁性能这一单值的影响，为贴合实际，后续可结合导热方程对耦合器的主从动盘的温度传导进一步完善理论。

4）试验测得磁力耦合器不同负载工况下，输出转矩和输出转速的试验值与模拟值、计算值在较大气隙与较小转速差下具有很好的一致性，为进一步完善磁力耦合器传动性能研究提供新的参考。

参 考 文 献：

［1］"KONG D， WANG D， LI W， et al. Analysis of a novel flux adjustable axial flux permanent magnet eddy current coupler[J].IET Electric Power Applications（WileyBlackwell），2023，17（2）：181.

［2］"吴俊. 磁体旋转型盘式磁力耦合器的电磁场特性及调速性能研究[D]. 镇江： 江苏大学， 2020.

［3］"YANG X， LIU Y， WANG L. An improved analytical model of permanent magnet eddy current magnetic coupler based on electromagneticthermal coupling[J]. IEEE Access， 2020， 8： 95235.

［4］"FU C， WANG D， ZHAO Q. A compact and couplingsmooth magnetic coupler design for AGV wireless charging application[J]. IEEE Access， 2023， 11： 11288.

［5］"杨超君，吉城龙，张秀文，等.筒式异步磁力耦合器的转矩与调速关系研究[J].电机与控制学报，2019，23（1）：108.

YANG Chaojun，JI Chenglong，ZHANG Xiuwen，et al.Torque and adjustablespeed relation for drumtype asynchronous magnetic couplers[J]. Electric Machines and Control，2019，23（1）：108.

［6］"MIN KC， CHOI JY. Eddycurrent loss analysis of noncontact magnetic device with permanent magnets based on analytical field calculations[J].IEEE Transactions on Magnetics，2015，51（11）：1.

［7］"LUBIN T， REZZOUG A. Improved 3D analytical model for axialflux eddycurrent couplings with curvature effects[J]. IEEE Transactions on Magnetics， 2017， 53（9）： 1.

［8］"DAI X， LIANG Q， CAO J， et al. Analytical modeling of axialflux permanent magnet eddy current couplings with a slotted conductor topology[J]. IEEE Transactions on Magnetics， 2016， 52（2）： 1.

［9］"杨超君，朱莉，吴盈志，等.开槽型盘式异步磁力耦合器调速特性[J].电机与控制学报，2021，25（11）：130.

YANG Chaojun，ZHU Li，WU Yingzhi，et al.Speedcontrol characteristics of slottedtype axialflux asynchronous magnetic couplers[J]. Electric Machines and Control，2021，25（11）：130.

［10］"杨超君，袁爱仁，陈子清，等.盘式实心异步磁力耦合器的机械特性与调速特性[J].电机与控制学报，2019，23（5）：110.

YANG Chaojun，YUAN Airen，CHEN Ziqing，et al.Mechanical properties and adjustablespeed characteristics of axialfluxsolidtype asynchronous magnetic couplers[J].Electric Machines and Control，2019，23（5）：110.

［11］"陈子清. 机电磁耦合系统中磁体旋转调速型磁力耦合器的工作性能研究[D]. 镇江： 江苏大学， 2020.

［12］"ZHANG H， WANG D， NING Y， et al. Performance study of axialflux eddy currentcoupler based on the equivalent circuit model[J]. IEEE Access， 2018， 6： 65679.

［13］"TIAN M， ZHAO W， WANG X， et al. Analysis on a novel flux adjustable permanent magnet coupler with a doublelayer permanent magnet rotor[J]. IEEE Transactions on Magnetics， 2018， 54（11）： 1.

［14］"ZHENG D， WANG D， LI S， et al. Electromagneticthermal model for improved axialflux eddy current couplings with combine rectangleshaped magnets[J].IEEE Access，2018，6：26383.

［15］"章友京. 盘式异步磁力耦合器变负载调速系统的工作性能研究[D]. 镇江： 江苏大学， 2016.

［16］"柳康. 磁体旋转型盘式调速异步磁力耦合器的传动性能与调速节能研究[D]. 镇江： 江苏大学， 2018.

［17］"WANG J. A generic 3D analytical model of permanent magnet eddycurrent couplings using a magnetic vector potential formulation[J]. IEEE Transactions on Industrial Electronics， 2022， 69（1）： 663.

［18］"邰蒋西. 磁体旋转型鼠笼盘式磁力耦合器机械特性预测及调速性能分析[D]. 镇江： 江苏大学， 2021.

［19］"王秀和.永磁电机[M].北京：中国电力出版社，2011.

［20］"谢德馨， 杨仕友. 工程电磁场数值分析与综合[M]. 北京： 机械工业出版社， 2009.

［21］"卢晓慧， 梁加红. 表面式永磁电机气隙磁场分析[J]. 电机与控制学报， 2011， 15（7）： 14.

LU Xiaohui，LIANG Jiahong.Air gap magnetic field analysis of surfacemounted permanent magnet motors[J].Electric Machines and Control，2011， 15（7）： 14.

［22］"RUSSELL R L， NORSWORTHY K H. Eddy currents and wall losses in screenedrotor induction motors［J］. Proceedings of the IEEPart A： Power Engineering， 1958， 105（20）： 163.

（编辑：邱赫男）

收稿日期： 2023-05-15

基金项目：国家自然科学基金（51875254）

作者简介：杨超君（1965—），女，博士，教授，博士生导师，研究方向为磁力机械及激光加工技术；

戚玉堂（2000—），男，硕士研究生，研究方向为磁力传动；

丁逸飞（1997—），男，硕士研究生，研究方向为磁力传动；

张意雯（1999—），女，硕士研究生，研究方向为磁力传动。

通信作者：杨超君