不平衡电网下双dq坐标变换的M3C微分平坦控制策略

摘 要：

针对目前模块化多电平矩阵变换器（M3C）研究中常用的双αβ 坐标变换解耦不彻底、传统PID控制方法效果差、不平衡工况研究少等问题，在分析拓扑结构和数学模型的基础上，采用双dq坐标变换对电气量进行解耦，建立了M3C的输入输出侧数学模型，分别对电压、电流进行正负序分离，并结合微分平坦理论，推导了输入侧、输出侧的微分平坦控制（DFC），最后模拟了两种不平衡工况下的运行情况。仿真结果表明，与线性PID控制相比，非线性的微分平坦控制提高了内环电流的跟踪速度和精度，更适用于非线性的M3C系统。在电网平衡或电网出现不对称故障时，微分平坦控制下M3C系统的动态稳定性与快速性更好，电能质量更高，电流谐波含量最多可以降低142%，能够更有效地抑制负序电流。

关键词：海上风力发电；模块化多电平矩阵变换器；不平衡电网；双dq坐标变换；微分平坦控制；PID控制

DOI：10.15938/j.emc.2024.01.005

中图分类号：TM762

文献标志码：A

文章编号：1007-449X（2024）01-0049-12

Differential flatness control strategy of modular multilevel matrix converter based on double dq coordinate transformation under unbalanced grid conditions

CHENG Qiming，"DU Tingwei，"LAI Yusheng

（College of Automation Engineering， Shanghai University of Electric Power， Shanghai 200090， China）

Abstract：

Aiming at the problems of incomplete decoupling of double αβ coordinate transformation commonly used in modular multilevel matrix converter （M3C） research， on the basis of the analysis of topological structure and mathematical model， poor effect of traditional PID control method， and little research on unbalanced working conditions， etc.， double dq coordinate transformation was adopted to decouple the electrical quantity. The mathematical model of M3C’s input and output side was established， the voltage and current were separated in positive and negative order， and the differential flatness control （DFC） of the input side and the output side was derived by combining the differential flatness theory. Finally， the operation under two unbalanced conditions was simulated. Compared with linear PID control， the simulation results show that nonlinear differential flat control improves the tracking speed and accuracy of inner loop current， and is more suitable for nonlinear M3C system. When the power grid balance or asymmetric fault occurs， M3C system under differential flat control has better dynamic stability and rapidity， higher power quality， and can suppress negative sequence current more effectively. The current THD can be reduced by up to 1.42%.

Keywords：offshore wind power; modular multilevel matrix converter; unbalanced grid; double dq coordinate transformation; differential flatness control； PID control

0 引 言

随着气候变暖、环境恶化等导致能源危机，新型清洁能源已成为了国家经济发展的方向之一[1-2]。其中海上风电由于具备稳定性强、可再生、受环境影响小等优势，极具开发前景。但如何将海上发电厂并入主电网正成为国内外海上风电领域的研究重点[3-4]。与常规的50 Hz的高压交流输电[5]和高压直流输电[6]相比，50/3 Hz的低频交流输电，又称分频传输系统，具有显著优势：可以提高交流海缆输电能力，只需一个AC/AC换流站，且设备投资成本少[7-9]。

在现有的AC/AC变换设备中，模块化多电平矩阵变换器（modular multilevel matrix converter，M3C）[10]由Erickson R和AI"Naseem O于2001年提出，作为直接AC/AC变换器具有高电压、大容量的优点。M3C拓扑由9条桥臂构成，以3×3矩阵形式排布，每条桥臂的电压、电流分量均包含两种不同频率的交流分量，存在强耦合现象，控制难度大。目前国内外学者已经对M3C的控制策略开展了一些研究，最为普遍应用的是基于双αβ0坐标变换的解耦控制方法。文献[11]的αβ0变换方法仅能将M3C的输入电流和输出电流解耦。文献[12-14]提出双αβ0变换，能将桥臂电流中的输入电流、输出电流和环流完全解耦，同时增加了两个对角维度的平衡控制，控制桥臂能量均衡分布。文献[15]将预测控制用于M3C中，然而M3C包含大量的状态变量，导致参数复杂、计算量庞大不具有实用性。文献[16-17]研究了双αβ0变换的非线性无源控制和微分平坦控制，系统跟踪速度有很大提升。尽管双αβ0变换被广泛采纳，但是这种控制方案也存在缺点，其被控量都是交流量，物理概念易混淆，且功率分量计算复杂。文献[18]提出了双dq坐标变换的方法，采用直流量作为内环被控量，但其采用的PID控制不仅调参复杂，而且是线性控制方法，作用在非线性的M3C上并不能使系统迅速稳定。到目前为止，采用双dq解耦方法的研究较少，并且其中未有文献考虑在发生不平衡故障时的非线性控制方案。非线性的微分平坦控制（differential flatness control，DFC）对系统稳定性的提升，超调量的降低等方面颇具优势，在电力电子领域和清洁能源领域已成为了研究热点[19-20]。与线性PID控制相比，DFC控制能使M3C系统稳定运行，避免因内外部扰动而发生动态特性变差的现象，提高内环电流的跟踪速度和精度。

本文首次提出在不平衡电网下将微分平坦控制策略应用到基于双dq坐标变换的M3C控制中。首先给出M3C的拓扑结构与工作原理，建立M3C在双dq坐标变换下的数学模型，然后在输入侧与输出侧出现不对称故障时，将电压电流正负序分离，进一步运用微分平坦理论，设计输入侧、输出侧的DFC控制器。最后，在MATLAB/Simulink平台上建立两种不平衡工况，分别模拟DFC控制和传统PID控制，通过仿真验证在电网电压不平衡条件下，采用DFC控制能使系统稳定运行，且效果优于传统PID控制。

1 M3C的电路结构及数学模型

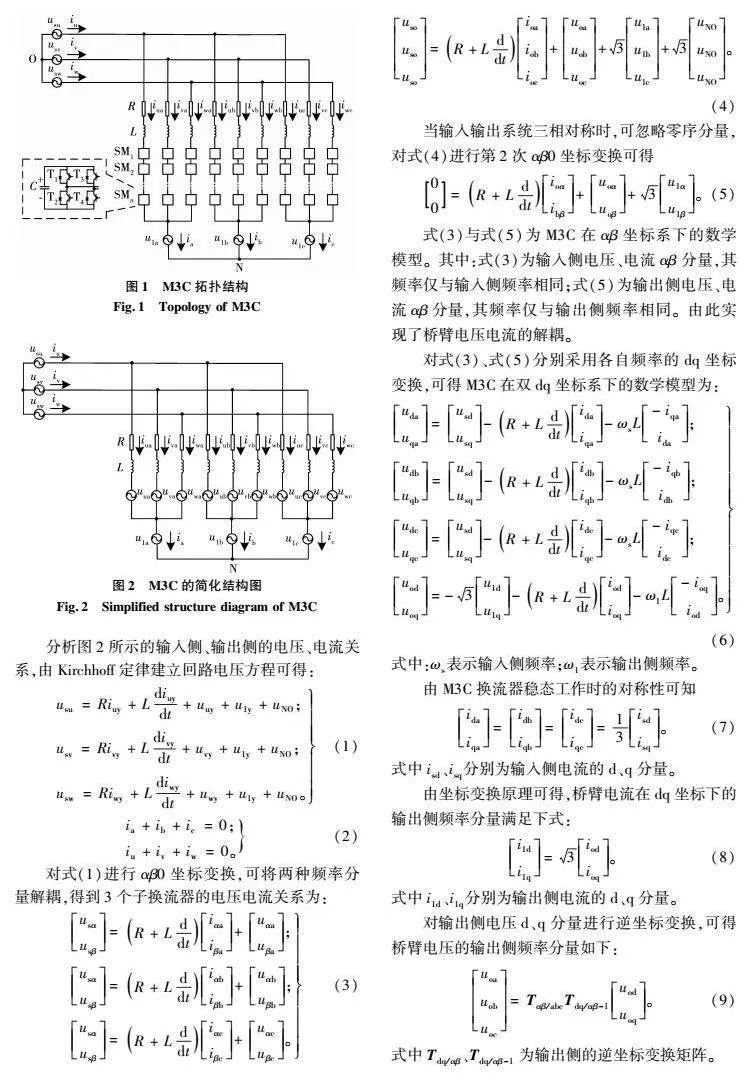
M3C变换器的主电结构如图1所示。M3C以H全桥子模块（用SM表示，由T1～T4 4个IGBT和1个电容组成）为基本单元，等效电阻R、电感L以及n个子模块级联构成1个换流桥臂，共有9个桥臂，可分为3个子换流器。M3C的输入侧是低频三相交流电源，输出侧是工频三相交流电源。

图1中：输入侧交流电压为usu、usv、usw，电流为iu、iv、iw；输出侧交流电压为u1a、u1b、u1c，电流为ia、ib、ic；桥臂电流为ixy，桥臂总电容电压为ucxy（x=u、v、w，y=a、b、c），uNO为共模电压。可以将每个桥臂的子模块视为受控电压源，得到图2所示的简化结构图。

分析图2所示的输入侧、输出侧的电压、电流关系，由Kirchhoff定律建立回路电压方程可得：

对式（1）进行αβ0坐标变换，可将两种频率分量解耦，得到3个子换流器的电压电流关系为：

当输入输出系统三相对称时，可忽略零序分量，对式（4）进行第2次αβ0坐标变换可得

式（3）与式（5）为M3C在αβ坐标系下的数学模型。其中：式（3）为输入侧电压、电流αβ分量，其频率仅与输入侧频率相同；式（5）为输出侧电压、电流αβ分量，其频率仅与输出侧频率相同。由此实现了桥臂电压电流的解耦。

对式（3）、式（5）分别采用各自频率的dq坐标变换，可得M3C在双dq坐标系下的数学模型为：

式中：ωs表示输入侧频率；ω1表示输出侧频率。

由M3C换流器稳态工作时的对称性可知

式中isd、isq分别为输入侧电流的d、q分量。

由坐标变换原理可得，桥臂电流在dq坐标下的输出侧频率分量满足下式：

式中i1d、i1q分别为输出侧电流的d、q分量。

对输出侧电压d、q分量进行逆坐标变换，可得桥臂电压的输出侧频率分量如下：

式中Tdq/αβ、Tdq/αβ-1为输出侧的逆坐标变换矩阵。

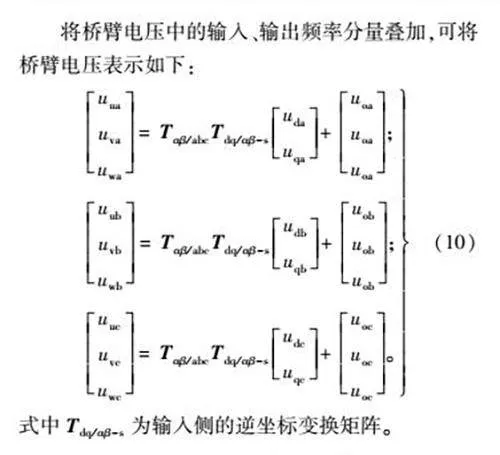
将桥臂电压中的输入、输出频率分量叠加，可将桥臂电压表示如下：

式中Tdq/αβ-s为输入侧的逆坐标变换矩阵。

2 不平衡电网下微分平坦控制策略

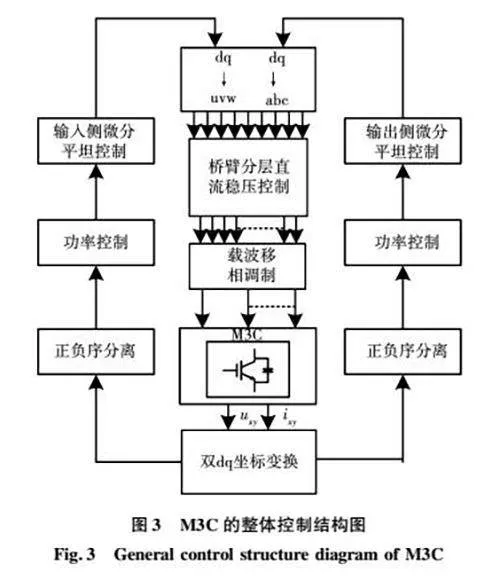
在不平衡工况下，M3C系统中会出现负序分量，导致过电流和非特征谐波的产生，影响控制效果，甚至烧毁元器件，对系统的安全稳定运行造成威胁，所以本文旨在研究基于M3C系统在不对称故障条件下的控制策略。图3为不平衡电网下M3C的总体控制结构图，其控制策略包括输入侧控制、输出侧控制、正负序分离、功率控制、桥臂分层直流稳压控制以及载波移相调制。

1）正负序分离：运用双dq坐标变换对输入侧和输出侧的电压、电流进行解耦，然后分别计算出正、负序电压电流分量；

2）功率控制：根据不平衡工况下M3C的运行要求，引入功率控制来求解期望电流值；

3）输入/输出侧控制：基于微分平坦理论，推导出输入侧、输出侧的DFC控制器；

4）子模块独立均压控制：用于平衡桥臂的子模块电容电压，此控制有利于保证系统的安全稳定运行。

2.1 正负序分离

当三相系统不对称时，系统中将会出现负序分量，导致系统出现过电流，会严重威胁整个系统的安全稳定运行[21]。因此，需要分离电气量中的正、负序分量，分别提取电压、电流的正序分量和负序分量，再设计相应的正、负序的控制策略。由于篇幅限制，本文仅以输入侧为例，系统的电压、电流可表示为

式中：β=ω+t+α+，ω+=ωs；γ=ω－t+α－，ω－=－ωs；α+、α－分别为正、负序分量的初相角；fuvw表示输入侧系统的电压或电流；f+、f-分别为正、负序分量的幅值；f0为零序分量。本文系统为三相三线制，无零序回路，所以可以忽略零序分量。

三相坐标系向两相旋转坐标系转换的正负序矩阵分别为：

对式（11）进行正负序dq变换可得：

将式（13）延迟π/2，可得

联立式（13）和式（14）可将正负序分离如下：

2.2 功率控制

根据瞬时无功功率理论，可将瞬时有功功率和无功功率表示为：

式中：P0是有功功率的直流分量；Q0是无功功率的直流分量；Ps2为有功功率的正弦2倍频分量；Pc2为有功功率的余弦2倍频分量；Qs2为无功功率的正弦2倍频分量；Qc2为无功功率的余弦2倍频分量。

将式（16）整理后，其矩阵形式如下：

根据常见不平衡工况的负面影响，可将系统控制目标设为：1）平衡电网电流；2）消除有功功率纹波；3）消除无功功率纹波。对应的电流期望值分别如下：

2.3 输入/输出侧平坦控制

微分平坦控制多用于连续时间的非线性控制系统中，能快速、准确地跟踪参考值，主要由前馈期望量和误差反馈补偿量组成，其理论框图如图4所示。

首先分析微分平坦理论的基本原理。

设非线性系统为：

式中u、y、x分别为系统的输入变量、输出变量和状态变量。

微分平坦理论的判断条件为：

式中λ1、λ2均为正整数，它们分别为状态变量、输入变量的微分阶数。

微分平坦控制策略框图如图4所示：uref，c为前馈控制量；uref，b为误差反馈补偿值；uref为参考输入量；y为输出实际值；yref为其期望值；Δy为两者误值；Δyref为Δy的期望值。

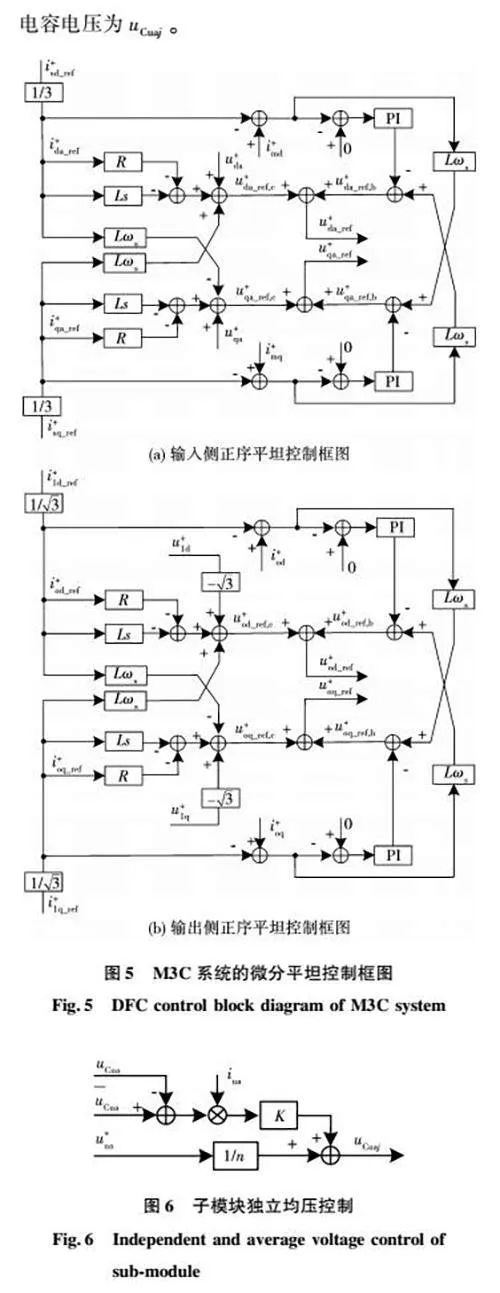
由于3个子换流器的结构相同，控制器也相同，本文仅以a相的子换流器为例具体分析。另外，正、负序分量的控制类似，在此仅推导正序分量的控制过程。根据式（6），可以推出输入侧正序的平坦控制器的前馈控制量为

式中u+da_ref，c、u+qa_ref，c分别为输入电流参考值i+da_ref、i+qa_ref生成的前馈控制量。

将系统状态变量误差表示为：

将式（24）代入式（6），可得误差模型如下：

由式（25）可得相应误差反馈补偿值为

式中：kDFp、kDFi为PI参数；u+da_ref，b、u+qa_ref，b分别为Δi+da、Δi+qa与参考值生成的误差反馈补偿值。

令Δi+da_ref=0，Δi+qa_ref=0，可得

联立式（6）和式（27）可得

由式（28）可得d、q轴电流的闭环传递函数如下：

因此，上述设计的M3C平坦控制器能实现电气量的解耦，响应速度快，跟踪效果好。

类似地，可以推导出输入侧b相子换流器、c相子换流器以及输出侧的正序前馈控制量、误差反馈补偿量和平坦控制器分别为：

M3C输入侧、输出侧正序平坦控制的详细框图如图5所示。

2.4 子模块独立均压控制

本文采用子模块独立均压控制使各子模块的电容电压达到稳定、均衡，其具体原理为：通过每个桥臂上的电流、对应桥臂的直流电压、单个子模块的电容电压，结合输入侧、输出侧的平坦控制信号，得出最终的桥臂控制信号，再送入载波移相调制，以此保证子模块电容电压的稳定。控制框图见图6。

以桥臂ua为例，其总电容电压uCua，子模块平均电容电压为u-Cua，调制信号为uua，第j个子模块的电容电压为uCuaj。

3 仿真实验分析

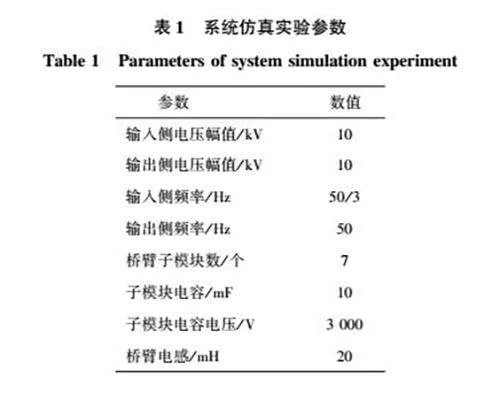
本文在 MATLAB/Simulink仿真平台上对图1所示M3C系统进行了模拟。由此设计了两种不平衡故障工况，分别仿真了微分平坦控制与传统的PID控制，并对比仿真效果。系统仿真参数如表1所示。

3.1 工况1实验分析

在工况1下，由控制目标1（平衡电网电流）变为控制目标2（消除有功功率纹波）再变回控制目标1。具体如下：

1）0～0.1 s内，电网电压无故障，系统正常运行，此时输入侧、输出侧均选择控制目标1，且P0=12 MW，Q0=0；

2）0.1～0.2 s内，输出侧电压a相跌落20%，构造输出侧三相电压不对称工况，此时输出侧选择控制目标2，且P0=6 MW，Q0=0，输入侧无变化；

3）0.2～0.3 s内，输入侧电压u相跌落20%，构造输入侧、输出侧三相电压均不对称的工况，输入侧输出侧均选择控制目标2；

4）0.3～0.4 s内，设定输入侧、输出侧电压恢复原值，交流系统对称，回到无故障正常运行工况。

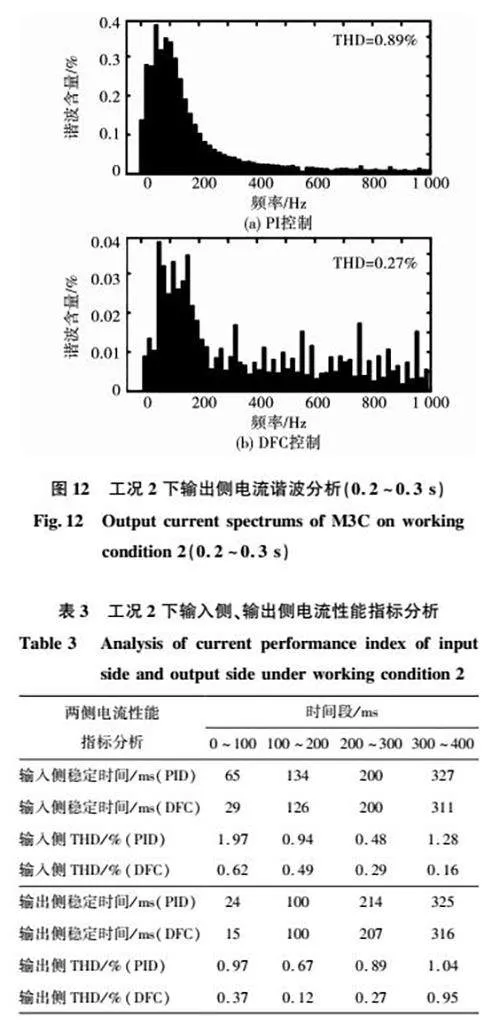
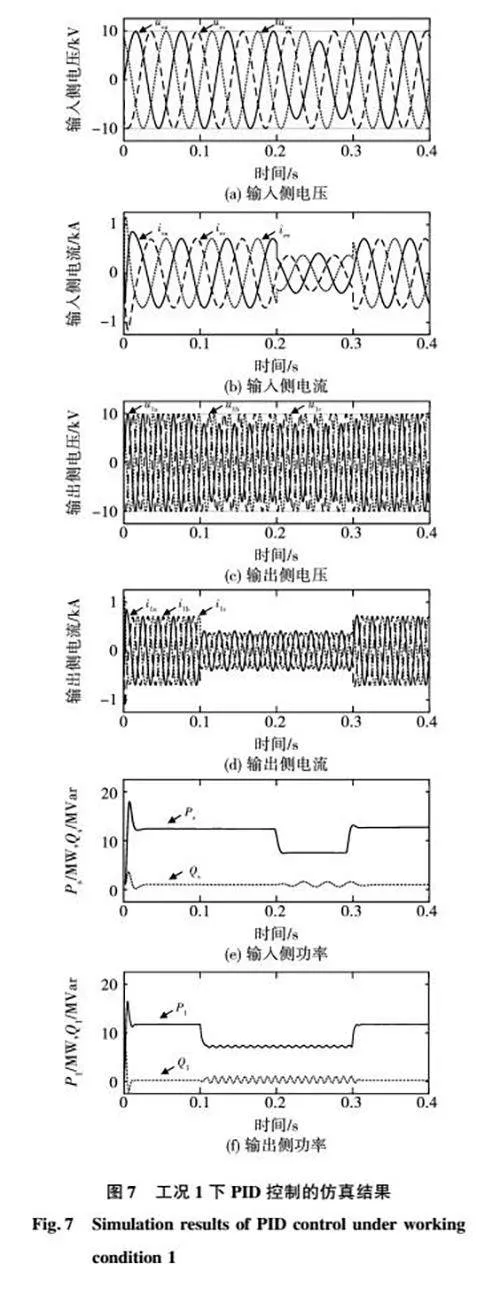
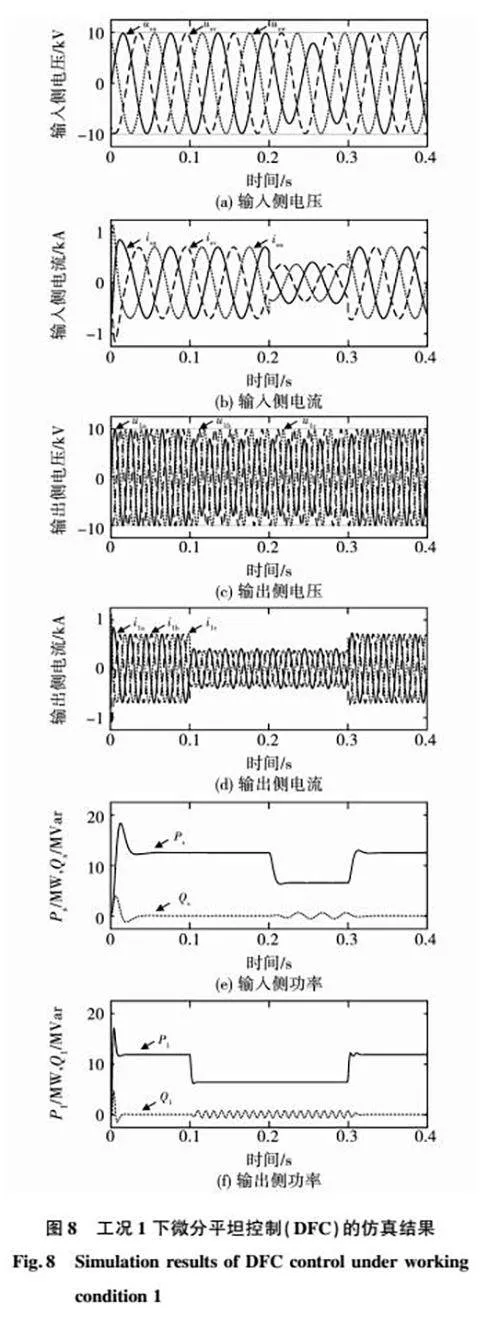
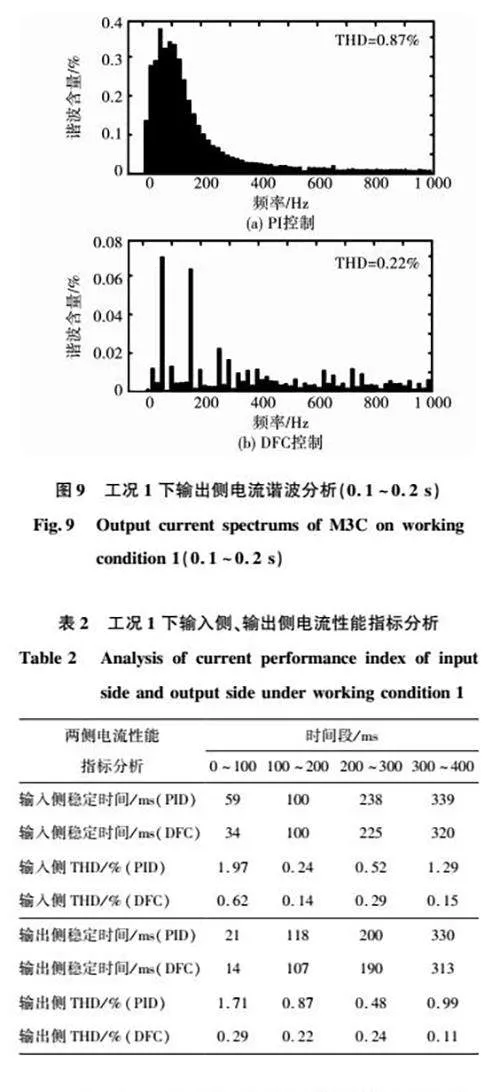
图7和图8为工况1下PID控制策略与微分平坦控制策略的仿真波形，包括输入侧电压usu/usv/usw、输入侧电流isu/isv/isw、输出侧电压u1a/u1b/u1c、输出侧电流i1a/i1b/i1c、输入侧有功无功功率Ps/Qs、输出侧有功无功功率P1/Q1。表2分别列出了工况1下PID控制策略与微分平坦控制策略的输入侧电流、输出侧电流的性能指标，并从稳定时间与总谐波畸变率（total harmonic distortion，THD）两个方面来进行对比分析。由于篇幅有限，本文截取了0.1～0.2 s内输出侧电流的THD值制成图9，其余THD值将直接表示在表2中。

分析图7、图8、图9和表2可知，在电网出现不对称故障时，传统PID控制策略与本文所提的微分平坦控制策略均能达到控制要求，保证系统稳定运行，且微分平坦控制策略下各电气量的性能指标均优于传统PID控制。

1）0～0.1 s内，系统处于无故障正常运行状态，在控制目标1下，两种控制方法下的输入侧、输出侧电流都具有较好的三相对称性，系统在微分平坦控制下的稳定速度较PID控制稍快，电能质量较高；

2）0.1～0.2 s内，输出侧出现不对称故障，a相电压跌落20%，输出侧控制目标为消除有功功率纹波，两种控制方法下的输出侧电流，在不对称故障与功率改变后都能达到新的稳定值。PID控制下系统的输出侧电流iabc与输出侧功率P1/Q1在0118 s后稳定，输出侧电流THD值为087%；微分平坦控制下系统的输出侧电流iabc与输出侧功率P1/Q1在0107 s后稳定，输出侧电流THD值为022%，对比可知微分平坦控制下输出侧电流能够更快达到稳定，系统的谐波污染更低；

3）0.2～0.3 s内，输入侧和输出侧均出现不对称故障，控制目标均为消除有功功率纹波，PID控制和微分平坦控制下系统的输入侧电流iuvw的THD值分别为052%和029%，说明微分平坦控制下系统的电能质量高；

4）0.3～0.4 s内，输入侧、输出侧均恢复无故障正常运行状态，由表2可知，微分平坦控制下系统的能更快达到稳态，谐波含量更低，电能质量更高，能够更有效地抑制负序电流。

3.2 工况2实验分析

在工况2下，由控制目标1变为控制目标3再变回控制目标1。工况2具体如下：

1）0～0.1 s内，电网电压无故障，系统正常运行，此时输入侧、输出侧均选择控制目标1，且P0=12 MW，Q0=0。

2）0.1～0.2 s内，输入侧电压u相跌落20%，构造输入侧三相电压不对称工况，此时输出侧选择控制目标3，且P0=6 MW，Q0=0，输出侧无变化；

3）0.2～0.3 s内，输出侧电压a相跌落20%，构造输入侧、输出侧三相电压均不对称的工况，输入侧输出侧均选择控制目标3；

4）0.3～0.4 s内，设定输入侧、输出侧电压恢复原值，交流系统对称，回到无故障正常运行工况。

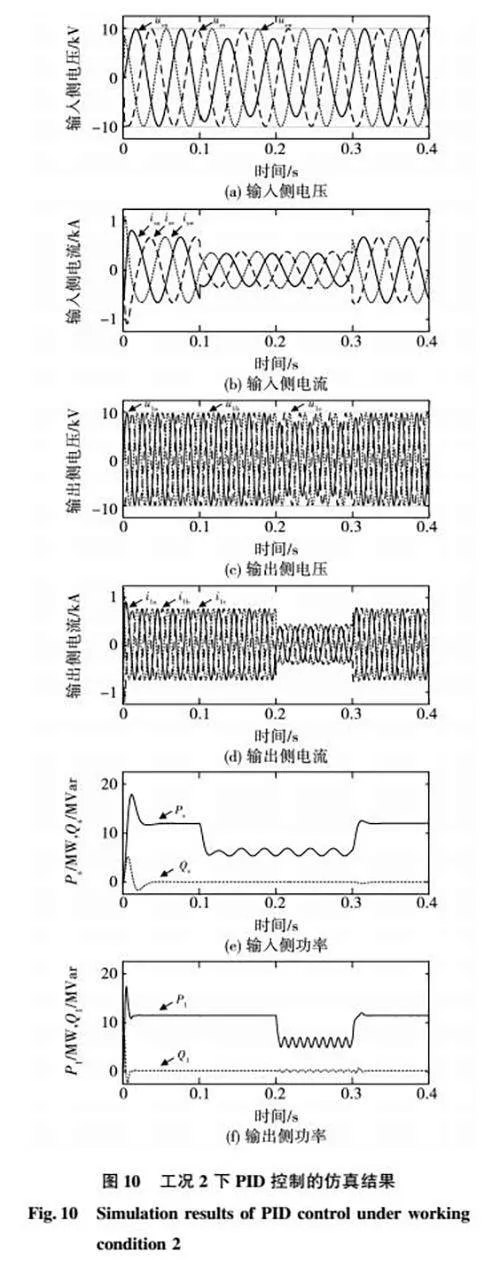
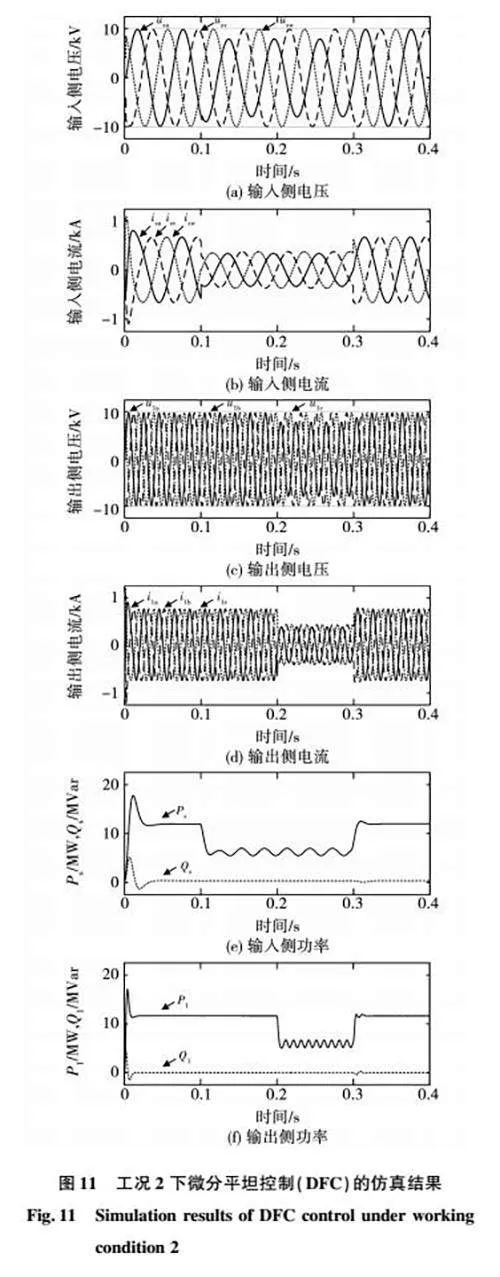
图10和图11为工况2下PID控制策略与微分平坦控制策略的仿真波形，包括输入侧电压usu/usv/usw、输入侧电流isu/isv/isw、输出侧电压u1a/u1b/u1c、输出侧电流i1a/i1b/i1c、输入侧有功无功功率Ps/Qs、输出侧有功无功功率P1/Q1。由于篇幅有限，本文截取了0.1～0.2 s内输出侧电流的THD值制成图12，其余THD值将直接表示在表中。表3分别列出了工况2下两种控制策略的输入侧电流、输出侧电流的性能指标，便于进一步对比分析。

分析图10、图11、图12和表3可知，在工况2下，微分平坦控制策略的控制效果优于传统PID控制。具体分析如下：

1）0～0.1 s内，系统为无故障正常运行状态；

2）0.1～0.2 s内，输入侧出现不对称故障，u相电压跌落20%，输入侧控制目标为消除无功功率纹波，两种控制方法下的输入侧、输出侧电流，在不对称故障与功率改变后都能迅速稳定；

3）0.2～0.3 s内，输入侧和输出侧均出现不对称故障，控制目标均为消除无功功率纹波，PID控制下系统的输出侧电流iabc与输出侧功率P1/Q1在0214 s后稳定，输出侧电流THD值为089%；微分平坦控制下系统的输出侧电流iabc与输出侧功率P1/Q1在0207 s后稳定，输出侧电流THD值为027%，对比可知微分平坦控制下动态稳定性与快速性更好，谐波污染更低；

4）0.3～0.4 s内，输入侧、输出侧均恢复无故障正常运行状态，由表3可知，微分平坦控制下系统的稳定速度、动态性能、控制效果均优于传统PID控制。

通过对比上述两种运行工况的仿真结果，不难得知无论是在正常运行工况下，或是系统出现单侧、双侧不对称故障的工况下，微分平坦控制的效果均优于PID控制。

4 结 论

本文对电网不平衡下的M3C微分平坦控制进行了深入研究。首先，根据双dq坐标变换建立了M3C的输入输出侧解耦模型，提取电压电流的正负序分量，基于微分平坦理论，设计出了输入侧、输出侧的微分平坦控制器，最后在MATLAB/Simulink平台上设计了两种不平衡工况，分别模拟了微分平坦控制和传统PID控制的运行效果，验证了本文所提控制策略的先进性。且通过理论分析和仿真对比可以得到以下结论：

1）双dq坐标变换中所有的受控量均为直流量，控制结构较双αβ更简单，实现容易，同时也具备优良的稳态和动态性能。

2）与传统的线性PID控制相比，非线性的平坦控制更适用于非线性的M3C系统。在平衡电网或电网出现不对称故障时，微分平坦控制下的控制效果均优于PID控制，其动态稳定性与快速性更好，谐波污染更低。

参 考 文 献：

［1］"YOU Shutang， ZHAO Jiecheng， YAO Wenxuan， et al. FNET/grideye for future high renewable power gridsapplications overview[C]// 2018 IEEE PES Transmission amp; Distribution Conference and ExhibitionLatin America （Tamp;DLA）， September 18-21， 2018， Lima， Peru. 2018： 1-5.

［2］"WU Jiahui， WANG Haiyun， WANG Weiqing， et al. Performance evaluation for sustainability of wind energy project using improved multicriteria decisionmaking method[J]. Journal of Modern Power Systems and Clean Energy， 2019， 7（5）： 1166.

［3］"KAWAMUR W， CHEN Kuanliang， HAGIWARA M， et al. A lowspeed， hightorque motor drive using a modular multilevel cascade converter based on triplestar bridge cells （MMCCTSBC）[J]. IEEE Transactions on Industry Applications， 2015， 51（5）： 3966.

［4］"HOSSAIN M I， ABIDO M A. Positivenegative sequence current controller for LVRT improvement of wind farms integrated MMCHVDC network[J]. IEEE Access， 2020， 8： 193314.

［5］"杨硕， 郭春义， 王庆， 等. 分层接入特高压直流输电系统协调控制策略研究[J]. 中国电机工程学报， 2019， 39（15）： 4357

YANG Shuo， GUO Chunyi， WANG Qing， et al. Coordinated control approach for UHVDC system under hierarchical connection mode[J]. Proceedings of the CSEE， 2019， 39（15）： 4357.

［6］"邓银秋， 汪震， 韩俊飞， 等. 适用于海上风电接入的多端柔直网内不平衡功率优化分配控制策略[J]. 中国电机工程学报， 2020， 40（8）： 2406.

DENG Yinqiu， WANG Zhen， HAN Junfei， et al. A novel chopper topology for grid side fault ride through in VSCHVDC based offshore wind power connection[J]. Proceedings of the CSEE， 2020， 40（8）： 2406.

［7］"LUO Jiajie， ZHANG Xiaoping， XUE Ying， et al. Harmonic analysis of modular multilevel matrix converter for fractional frequency transmission system[J]. IEEE Transactions on Power Delivery， 2020， 35（3）： 1209.

［8］"AlTAMEEMI M， MIURA Y， LIU J， et al. A novel control scheme for multiterminal lowfrequency AC electrical energy transmission systems using modular multilevel matrix converters and virtual synchronous generator concept[J]. Energies， 2020， 13（3）： 748.

［9］"MENG Yongqing， SHANG Shuonan， ZHANG Haitao， et al. IDAPB control with integral action of Yconnected modular multilevel converter for fractional frequency transmission application[J]. IET Generation Transmission amp; Distribution， 2018， 12（14）： 3386.

［10］"ERICKSON R W， AlNASEEM O A. A new family of matrix converters[C]// 27th Annual Conference of the IEEE Industrial Electronics Society， November 29December 2， 2001， Denver， USA. 2001： 1515-1520.

［11］"OATES C. A methodology for developing ‘Chainlink’ converters[C]// 13th European Conference on Power Electronics and Applications， September 8-10， 2009， Barcelona， Spain. 2009： 1-10.

［12］"KAMMERER F， KOLB J， BRAUN M. Fully decoupled current control and energy balancing of the modular multilevel matrix converter[C]// 15th International Power Electronics and Motion Control Conference （EPE/PEMC）， September 4-6， 2012， Novi Sad， Serbia. 2012： LS2a.3-1-LS2a.3-8.

［13］"KAWAMUR W， AKAGI H. Control of the modular multilevel cascade converter based on triplestar bridgecells （M2CCTSBC） for motor drives[C]//IEEE Energy Conversion Congress and Exposition （ECCE）， September 15-20， 2012， Raleigh， USA. 2012： 3506-3513.

［14］"KAWAMUR W， HAGIWARA M， AKAGI H. Control and experiment of a modular multilevel cascade converter based on triplestar cells[J]. IEEE Transactions on Industry Applications， 2014， 50（5）： 3537.

［15］"NADEMI H， NORUM L E， SOGHOMONIAN Z， et al. Low frequency operation of modular multilevel matrix converter using optimizationoriented predictive control scheme[C]// 2016 IEEE 17th Workshop on Control and Modeling for Power Electronics（COMPEL）， June 27-30， 2016， Trondheim， Norway. 2016： 1-6.

［16］"程启明， 马信乔， 江畅， 等. 模块化多电平矩阵换流器输入侧的无源控制策略[J]. 电力系统自动化， 2021， 45（11）： 137.

CHENG Qiming， MA Xinqiao， JIANG Chang， et al. Passivitybased control strategy for input side of modular multilevel matrix converter[J]. Automation of Electric Power Systems， 2021， 45（11）： 137.

［17］"程启明， 谢怡群， 马信乔， 等. 模块化多电平矩阵变换器的平坦控制策略[J].电力自动化设备， 2022， 42（1）： 187.

CHENG Qiming， XIE Yiqun， MA Xinqiao， et al. Flat control strategy for modular multilevel matrix converter[J]. Power Automation Equipment， 2022， 42（1）： 187.

［18］"孟永庆， 王健， 李磊， 等. 基于双 dq 坐标变换的M3C变换器的数学模型及控制策略研究[J]. 中国电机工程学报， 2016， 36（17）： 4703.

MENG Yongqing， WANG Jian， LI Lei， et al. Research on modeling and control strategy of modular multilevel matrix converter based on double dq coordinate transformation[J]. Proceedings of the CSEE， 2016， 36（17）： 4703.

［19］"宋平岗， 周鹏辉， 肖丹， 等. MMCRPC的功率同步平坦控制策略[J]. 电力自动化设备， 2019， 39（11）： 146.

SONG Pinggang， ZHOU Penghui， XIAO Dan， et al. Power synchronization flatness control strategy of MMCRPC[J]. Power Automation Equipment， 2019， 39（11）： 146.

［20］"SHAHIN A， MOUSSA H， FORRISI I， et al. Reliability improvement approach based on flatness control of parallelconnected inverters[J]. IEEE Transactions on Power Electronics， 2017， 32（1）： 682.

［21］"张翀. 模块化多电平矩阵换流器在AC/AC 系统应用中的关键技术研究[D]. 杭州： 浙江大学， 2020.

（编辑：刘琳琳）

收稿日期： 2022-12-09

基金项目：国家自然科学基金（62303301）；上海市电站自动化技术重点实验室资助项目（13DZ2273800）

作者简介：程启明（1965—），男，博士，教授，研究方向为电力系统自动化、发电过程控制、先进控制及应用；

杜婷伟（2000—），女，硕士研究生，研究方向为新能源发电控制、海上风力发电控制；

赖宇生（1996—），男，硕士研究生，研究方向为新能源发电控制、电力电子控制。

通信作者：杜婷伟