基于虚拟阻抗优化的VSG暂态功角稳定自适应控制策略

摘 要：

在电网短路故障发生的情况下，虚拟同步发电机系统不仅会发生暂态功角失稳，同时还可能会出现过流。为了提升虚拟同步发电机的暂态功角稳定性及故障电流限制性能，首先建立了包含电压和电流控制环、虚拟阻抗及功率控制环结构的虚拟同步发电机系统的总体控制结构，给出了虚拟阻抗功率模型建立的理论依据。对无功功率控制环路恶化暂态功角稳定性，提出了设置电压增量自由控制支路来实现提高暂态功角稳定性的方法。其次，在无功功率控制环路及电压增量自由控制支路的共同作用下，对“不考虑切除故障”和“考虑切除故障”两种不同的运行工况，提出了能够同时满足暂态功角稳定性和故障电流限制的虚拟阻抗优化方法。最后提出了虚拟同步发电机的暂态功角失稳控制和故障电流限制的自适应控制算法，以满足实际运行工况的需求，通过Simulink仿真模型验证了所提自适应控制策略的有效性和可行性。

关键词：虚拟同步发电机；同步稳定性；等面积法则；虚拟阻抗；故障电流限制；李雅普诺夫稳定性

DOI：10.15938/j.emc.2024.01.004

中图分类号：TM46

文献标志码：A

文章编号：1007-449X（2024）01-0035-14

Improvement of transient stability performance of VSG considering power angle stability and fault current limiting

SUN Jiuliang，"CAI Wei，"GUO Qingbo

（School of Electrical and Electronic Engineering， Harbin University of Science and Technology， Harbin 150080， China）

Abstract：

In addition to transient power angle instability， the virtual synchronous generator system may also experience overcurrent in the event of a grid short circuit fault. In order to improve the transient power angle stability and fault current limiting performance of VSG， firstly， the overall control structure of virtual synchronous generator system including voltage and current control loop， virtual impedance and power control loop structure is established in this paper，the theoretical basis for establishing a virtual impedance power model is provided. Due to the activation of reactive power control loop， transient power angle stability will be reduced， a method of improving the power angle curve by setting the free control branch of the voltage increment is proposed. Secondly， with the combined effect of the reactive power control loop and the voltage increment free control branch， a virtual impedance optimisation method that can simultaneously satisfy transient power angle stability and fault current limitation is proposed for two different operating conditions， namely “without considering fault removal” and “considering fault removal”. Finally，adaptive control algorithms for transient power angle instability control and fault current limitation of virtual synchronous generators are proposed to meet the requirements of real operating conditions. The validity and feasibility of the control strategy proposed in this paper are verified by the simulation model.

Keywords：virtual synchronous generator; synchronous stability; equal area rule; virtual impedance; fault current limitation; Lyapunov stability

0 引 言

随着“双碳”战略的提出和实施，以风力、光伏为主导的大规模的清洁型能源（新能源）所产生的电能将会通过并网变流器流向电网。以同步发电机为主体的传统电力系统将会逐渐被以变流器为并网接口的新能源所替代[1]。目前，并网变流器通过锁相环（phase locked loop，PLL）与电网保持同步的运行方式还处于主导地位，其优势在于通过使用最大功率跟踪（maximum power point tracking，MPPT）控制器可以使系统输出最大功率[31-32]。然而，由于其本身不具备惯性及阻尼特性，大规模的使用将会导致电网的惯性降低、阻尼变弱。除此之外，当交流电网的短路比（short circuit ratio，SCR）接近13时，由于PLL的负面影响，基于PLL同步型的并网变流器难以保证其控制稳定性[2-3]。同时，受功率半导体器件过载能力的限制，变流器过载能力相对较弱。上述差异性对电力系统的稳定运行带来了新的挑战。

针对电力系统存在的低惯性、弱阻尼的特征。目前，面对分布式电源接入的微电网系统，具备组网能力的虚拟同步发电机（virtual synchronous generator，VSG）技术逐渐成为一种可行的解决方案，理论上这一技术可以使微电网当中的并网变流器表现出和传统同步发电机（synchronous generator，SG）完全相同的外特性。同时，这种控制策略使并网变流器能够在超弱交流电网下稳定运行，SCR几乎等于1[4]。

从目前看来，VSG要比SG更加灵活可控，可以通过对控制算法的优化进一步提升小信号稳定性，进而提高虚拟同步发电机在惯性提供、调频和调压方面的性能。随着基于线性系统理论（如特征值和频率分析）工具应用的成熟，VSG的小信号稳定性已从不同方面进行了广泛研究，如小信号动态特性、与SG的差异、建模和参数设计、具有改进小信号稳定性的新型VSG等。然而，小信号稳定性是实现暂态功角稳定的必要条件，而不是充分条件。

在大信号稳定性的研究工作范畴当中，作为一种功率同步型变流器控制技术，尽管文献[5-6]证明了组网控制比跟网控制在弱电网中表现出更好的暂态功角稳定性。并且文献[7]已经证明了基于下垂控制的并网逆变器的暂态功角稳定性要强于同步发电机。然而，由于其不能为电网提供惯性，这可能会对高渗透率的电网稳定性带来严重挑战。由于虚拟同步发电机与同步发电机工作原理的相似性，虚拟同步发电机在严重故障下同样面临过流的风险和功率振荡[8-13]。因此，随着虚拟同步发电机技术在逆变器控制技术方向上的发展，其暂态功角稳定性的研究工作变得越来越重要。

在以往的针对VSG的暂态功角稳定性的研究工作内容当中，不仅涉及到不同类型虚拟同步发电机的暂态功角稳定性问题[14-16]。而且也关注了环路参数对暂态功角稳定性的影响，同时也有考虑到有功功率环和无功功率环结构的不同对VSG的暂态功角稳定性的影响[5-6，17-20]。比如，文献[20]研究了惯量对暂态功角稳定性的影响，发现大惯量有利于首摆稳定性，但不利于全局稳定性，配置合适的惯量有助于平衡VSG的首摆稳定性和全局稳定性。文献[18]已经证明了在低惯量和弱阻尼条件下，转矩形式的有功功率控制环路比功率形式的有功功率控制环路具有更好的稳定性，且两者的差异随着惯量的增大而减小。又比如，由于在电网电压跌落时，变换器端电压与电网电压的相角差将导致输出无功功率突增。由无功功率环路下垂关系可知，输出无功功率增加将导致参考电压幅值的下降，并同时带来变换器输出有功功率的减小，加剧了故障期间变换器输出有功功率和参考有功功率的不平衡，导致无功功率控制环路会对暂态功率角稳定性产生“恶化效应”[17]。因此，在分析VSG系统的暂态功角稳定性时，无功功率环路不可以忽视，因为当系统发生大扰动时，VSG的无功功率环路会影响电压指令值的幅值。尽管文献[30]提出了基于无功功率控制环路频率前馈的暂态功角稳定性提升方法。文献[20]提出了通过将角加速度的动态引入到无功功率控制环路中，通过提高功角曲线来提高暂态功角稳定性的方法。然而，由于两者对电压指令增量没有建立约束条件，由此可能产生的过流问题并未得到认识和解决。

在以往的研究工作内容当中，虚拟阻抗被认为是一种很好的限流措施，并且可以实现动态调整，可以对功率响应特性和稳定性的提升起到重要作用。因此，可以通过设计虚拟阻抗来重塑VSG输出阻抗，进而提高VSG的稳定性。然而，如果输出阻抗的设计仅基于小信号稳定性分析。在大扰动发生的情况下，仅能满足小信号稳定性约束的输出阻抗不能保证系统的安全、稳定运行。

由于大扰动类型的故障（如短路故障和线路跳闸）会导致过电流和暂态功角失稳等问题。文献[21]建立了包括虚拟阻抗在内的简化成网模型，并揭示了虚拟阻抗会危害功角稳定性，但动态性能和响应是未知的。文献[19]分析了不同结构的虚拟阻抗在电磁暂态过程中的动态性能，在电压指令恒定的条件下，对于I型扰动和II型扰动发生的情况，建立了同时满足电流限制约束和李亚普诺夫稳定性条件的虚拟阻抗边界。因此，在此基础之上，无功功率控制环路对暂态功角稳定性和过流的影响需要被考虑。

针对上述问题，首先近一步分析和考虑VSG的无功功率控制环路对暂态功角稳定性和过流的影响，通过设置不带增益系数的电压增量自由控制支路来实现功角曲线的抬升，进而提升暂态功角稳定性。其次，在电压增量没有建立约束条件的情况下，针对“不考虑切除故障”和“考虑切除故障”两种不同的运行工况，建立能够满足电流限制条件和李雅普诺夫稳定性条件的虚拟阻抗约束条件。提出满足VSG的暂态功角失稳控制和故障电流限制的自适应控制算法。最后，通过Simulink仿真模型验证了本文所提自适应控制策略的有效性和可行性。

1 模型的建立及分析

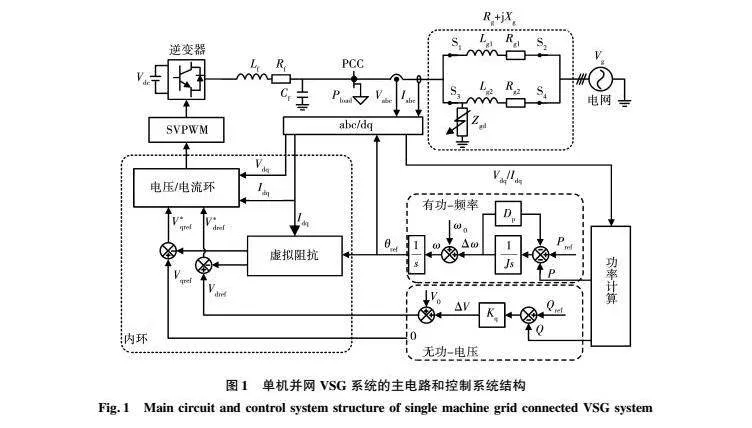
目前，由于单机无穷大系统已经成为暂态同步稳定研究工作的基础。因此，本文在基于dq轴旋转坐标系的控制框架下，建立了如图1所示单机无穷大三相并网VSG系统的主电路和控制系统结构。

由于文献[7]已经指出其暂态特性取决于故障期间的运行场景（是否有平衡点，是否触发电流限制），而不是具体的故障类型。因此，可以采用输电线路的三相短路故障模拟不同的故障运行场景。其中：Rg、Lg分别表示的是线路的电阻和电感，Vg表示电网的电压，两者共同构成电网的戴维南等效电路；S1～S4表示断路器；Rg1～Rg2表示线路电阻；Lg1～Lg2表示线路电感；Lf、Rf、Cf表示滤波器的电阻、电感和电容；Iabc是注入电网的电流矢量；Vpcc是PCC（公共耦合点）点的电压；VSG输出的有功功率在本文中用P表示，无功功率用Q表示，其参考值分别用Pref和Qref表示。由于直流测电压通常由储能变流器控制，在分析VSG的暂态功角稳定性时，可以认为直流测电压是恒定的。有功功率控制环提供角度参考值，无功功率控制环提供电压幅值的参考值。

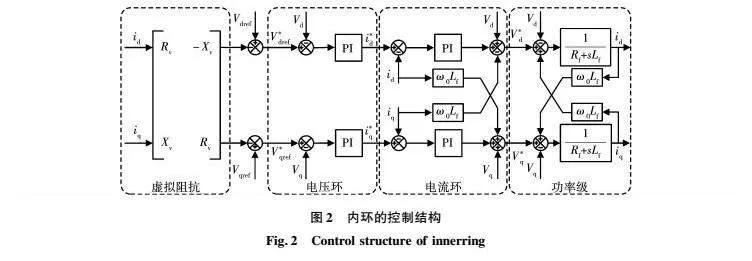
1.1 控制环路模型

内环控制部分具体内容如图2所示，虚拟阻抗采用虚拟复阻抗，电压控制环路和电流控制环路均采用比例积分（proportional integral，PI）控制器。值得注意的是，内环控制的时间尺度通常与外环控制的时间尺度存在数量级差别[13]。因此，由于他们存在时间尺度解耦，这2个环路的动态特性可以进行独立分析[14]。同时，由于电压环和电流环控制的引入，逆变器的等效阻抗和内部电压发生了变化，将会有助于暂态功角稳定性的提升[17-22]。

在有功功率控制环路中，ω被定义为VSG的角频率，在此基础之上，可以很容易推导出ω=ω0+Δω。由此，得到如下的有功功率控制律：

其中J和Dp分别表示虚拟惯量和调速器的增益。通过降低有功参考值Pref，在提高暂态功角稳定性的同时，降低了系统的频率稳定性。因此，应当尽量避免采取这一措施。

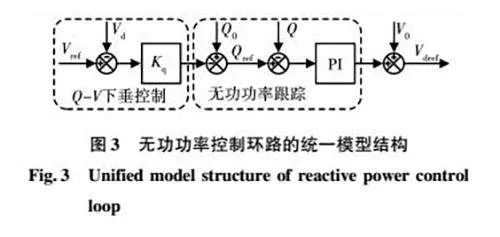
由于VSG的虚拟惯量与同步发电机的惯量实际作用效果存在明显差距，导致频率和电压控制效果存在较强的时间尺度上的耦合，无法忽略无功功率控制环路对暂态功角稳定性的影响[29]。为了研究不同的无功功率控制环路对暂态功角稳定性的影响，可以应用等面积法则（equal area criterion，EAC）函数和李雅普诺夫函数对VSG的暂态功角稳定性进行分析的无功功率控制环的统一模型结构被建立[20]，如图3所示。基于所提出的统一模型，可以分析验证不同无功功率控制环对VSG的暂态功角稳定性的影响。

尽管Q-V下垂控制对VSG的暂态功角稳定性的作用更加灵敏，然而，无功功率下垂系数Dq对VSG的暂态角稳定性的影响受Vd和Vref的状态的影响。随着电压指令Vref、参考无功功率和电容电压的增加，加速面积减小，减速面积增加。相反，随着电压指令Vref的减小，加速面积增加，减速面积减小。除此之外，无功功率控制环的响应速度与暂态功角失稳问题的时间尺度存在数量级差别，可以认为在故障发生后，无功功率控制环能够快速响应至稳态，因此，从这个角度来看，Vdref可以被视为一个参数变量，而不是作为一个状态变量来处理。

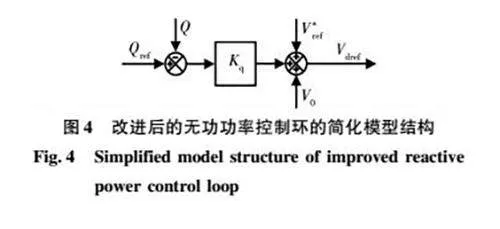
综合考虑上述因素，本文提出通过设置电压增量的自由控制支路来提高暂态功角稳定性的控制方法，如图4所示。其中Kq是无功功率的控制器增益，其控制律为

值得说明的是，Vref的增量大小如何设置将会在第3部分内容当中具体给出。

1.2 虚拟阻抗功率模型

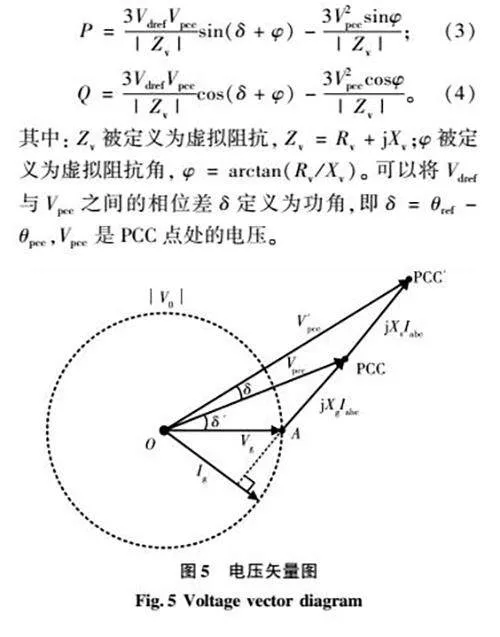
在不计滤波器阻抗、电网电阻Rg和虚拟电阻Rv的情况下，以电网电压Vg为参考向量，VSG的电压矢量图如图5所示。其中：PCC′是虚拟公共耦合点；δ′是Vg和Vpcc之间的相位差；δ是V′pcc（Vdref）和Vpcc之间的相位差；V′pcc是虚拟公共耦合点处的电压。根据电压矢量图可以发现δ′和δ同时稳定。如果δ′不稳定，δ就会发生振荡。因此，δ可以表征系统在PCC点电压骤降下的动态性能，也就是说可以表征VSG系统的暂态功角稳定性，这一发现为功率模型的建立奠定了理论基础。在此基础之上，根据图1及线路功率传输原理，VSG的输出有/无功功率可以建模如下：

其中：Zv被定义为虚拟阻抗，Zv=Rv+jXv；φ被定义为虚拟阻抗角，φ=arctan（Rv/Xv）。可以将Vdref与Vpcc之间的相位差δ定义为功角，即δ=θref-θpcc，Vpcc是PCC点处的电压。

2 虚拟阻抗约束条件及稳定性分析

2.1 Ⅰ型扰动：平衡点存在

暂态功角稳定性分析工作的主要难点在于提取其大信号的非线性动态响应。由于小信号建模方法和线性控制理论已不适用，通常基于非线性微分方程的理论分析又是一项非常繁琐的工作。因此，本文采用等面积法则和相位图相结合的方法进行暂态功角稳定性分析。

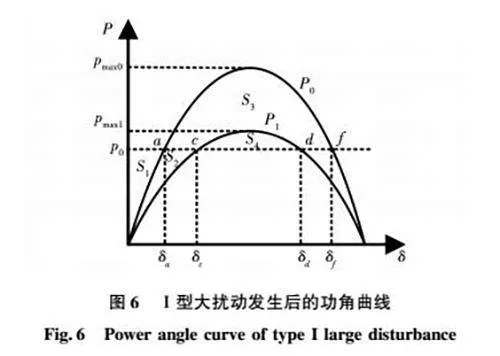
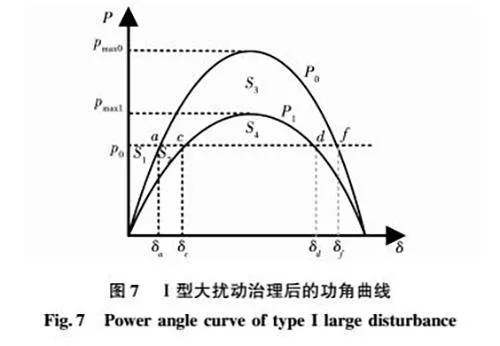
在不考虑阻尼影响的情况下，Ⅰ型大扰动发生后的功角失稳机理可以在基于等面积法则理论的基础之上用图6所示的功角曲线解释，其中实线P0为扰动发生前的功角曲线，其最大输出功率极限幅值为pmax0，a、f分别为其平衡点和不平衡点，δa和δf为对应的功角，并且δf=π-2φ-δa，减速面积S3（由曲线P0和p0的a、f段包围的区域）将大于加速面积S1（由曲线P0和p0的0、a段包围的区域）。其中实线P1为扰动发生后的功率角曲线，其最大输出功率极限为pmax1，c、d分别为其平衡点和不平衡点，δc和δd为对应功角，由于减速面积S4（由曲线P1和p0的c、d段包围的区域）将小于加速面积S1+S2的出现，导致功角将会越过δd（不稳定平衡点，有的文献当中也称之为最大临界点），出现功角震荡失稳。

假设在利用电压增量的自由控制支路动态调整电压指令的基础之上，通过对VSG的虚拟阻抗进行优化，为阻抗优化设计准则，能够正确响应PCC点电压和电流的变化，那么电磁暂态过流和暂态功角稳定性问题就有期望能够同时得到解决。

由于在大扰动发生后，电压、电流控制环路会出现最快的动态响应过程，因此，可以将故障发生后的电压指令的初始值Vdref0用于计算限流阻抗的边界。如果在电压、电流的动态变化过程中，忽略电压、电流控制环路的延迟所造成的影响。在dq轴坐标系当中，VSG的输出电流可以用下式表示：

其中：|Zv|表示阻抗的模值；δ0可以通过后文计算得出。如果PCC点的电压从V0下降到Vsag，在dq轴坐标系当中，VSG的输出电流的d轴和q轴分量可以分别写为：

根据Park反变换，可以很容易得到α-β参考坐标系中α轴的电流iα，即

通过求解式（7）的极大值可以获得电流的最大值，最大值的求解如下：

通过对式（7）求导数获得最大电流出现的时刻tmax，具体如下：

在确定电流极限值Imax以后，Imax值的选取主要取决于所采用的功率半导体器件的电流极限，一般在实际工程当中最低也要保持15IN的裕度。由此，可以导出限流阻抗的边界如下：

本文的贡献在于经过研究发现，在无功功率控制环路和不同结构的虚拟阻抗结构作用下，文献[19]当中提出的限流虚拟阻抗模型仍然适用。值得说明的是，为了保证稳态裕度，虚拟阻抗应当尽可能的小，这也就对功率器件的过流能力提出了更高的要求。

由于稳定平衡点处和不稳定平衡点处Δω=0。因此，在式（12）的基础之上，令Δω=0，可以推导出稳定平衡点处的功角如下式：

为保证平衡点的存在，稳定平衡点处的功角δa必须满足下式条件：

从式（13）中可以看出，随着虚拟阻抗、PCC点电压及电压指令值的变化，稳定平衡点和不稳定平衡点也将随着发生变化。同时，在Ⅰ型扰动发生后，稳定平衡点和不稳定平衡点仍然可以确定。而且，在式（13）和式（14）的基础之上，将大扰动发生后的相应变量代入其中，便可导出大扰动发生时平衡点存在的虚拟阻抗边界为

根据式（1）和式（3），在不考虑阻尼效应的情况下，大扰动发生后的VSG的转动方程可以用下式表示：

如图6所示，假设电压指令此时是一个定值，大扰动发生后的平衡点为（δc，Δω=0），将式（16）从这一点开始积分，可以得到如下函数：

从中不难看出，式（17）当中的函数是一个具有明确物理意义的函数，可以准确描述功率波动过程中动能Ek与势能Ep之间的转换，因此，在后面的分析中可以被当作李雅普诺夫能量函数来使用[19，24]。

值得注意的是，在考虑电压动态变化时，重新构建李雅普诺夫函数有一定的难度。为此，如果将电压指令值不再作为状态变量，而是作为参数变量，这一问题就可以得到解决。当确定某一参数变量Vdref，虚拟阻抗的边界就可以确定，而随着状态变量的改变，参数变量Vdref同样会改变，因此需要根据系统此时刻的运行状态求解下一时刻的参数变量Vdref，进而确定下一时刻的虚拟阻抗边界。

在Ⅰ型大扰动的情况下，将初始点（δa，Δω=0）代入式（17），可得初始能量V（δa，0）为

不稳定平衡点为（π-2φ-δc，Δω=0），因此，类似地，临界能量Vcr可导出为

根据李雅普诺夫稳定性判据，暂态功角稳定的虚拟阻抗边界可由下式确定：

此外，为了保证VSG在故障清除后仍然稳定运行，即当终端电压恢复到正常水平时，平衡点仍应存在，与式（15）类似，虚拟阻抗应当满足式（21）的条件。

经过提出的控制策略治理后的功角曲线如图7中实线P1所示，c、d为其平衡点和不平衡点，δc和δd为对应功角，减速面积S4将大于加速面积S1+S2。

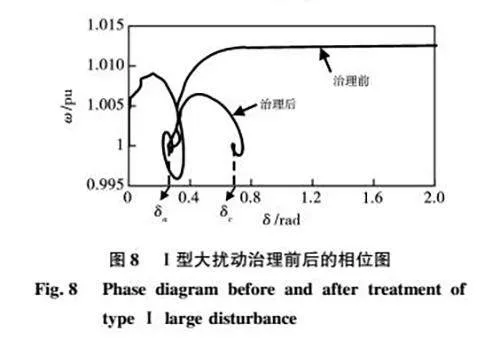
对于Ⅰ型扰动发生的情况，在Simulink仿真模型运行的过程中，提取出的相位图如图8所示。在故障发生时刻前，不管是经过治理的VSG系统和没有经过治理的VSG系统，平衡点都是（δa，Δω=0）。在故障发生后，没有经过治理的VSG的功角和频率一直增大，直到超出不稳定平衡点。然而，经过治理的VSG的频率和功角在经过一段时间波动以后，重新稳定在一个新的平衡点（δc，ω0）。

2.2 Ⅱ型扰动：平衡点不存在

2.2.1 不考虑切除故障

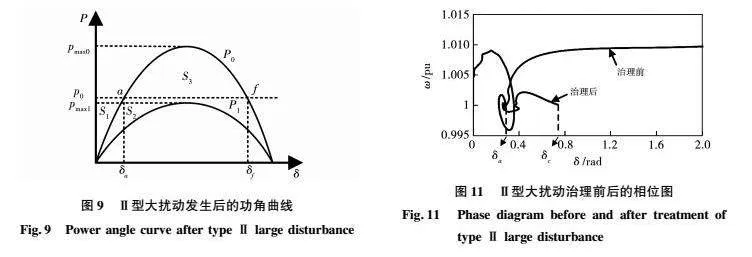
在三相短路故障发生期间，由于断路器故障或其他原因，可能会导致故障无法被切除，在这种情况下，仍然需要保证VSG系统与电网保持同步运行。如图9所示，在不考虑阻尼影响的情况下，Ⅱ型大扰动发生前的功角曲线为P0，大扰动发生后的功角曲线为P1，加速面积为S1+S2，减速面积为0，由于p0gt;pmax1，导致ω·gt;0，VSG的输出频率ω会一直处于增大的状态，功角δ也会一直增大，直至出现功角失稳状态。在这种情况下，VSG系统必须迅速采取措施保持稳定。如果要求在故障期间保持一定时间的稳定运行，那么就需要恢复平衡点。

针对平衡点不存在的情况，受文献[28]中恢复平衡点的思想启发。在不考虑切除故障的情况下，本文提出通过主动改变电压指令、功率指令调整的综合治理方法使平衡点恢复。同时，在平衡点恢复后，可以再次通过式（10）、式（15）、式（20）和式（21）确定新的阻抗边界。此外，本文提出了适用于新型控制策略的迭代算法，详细内容可见第3节所述。

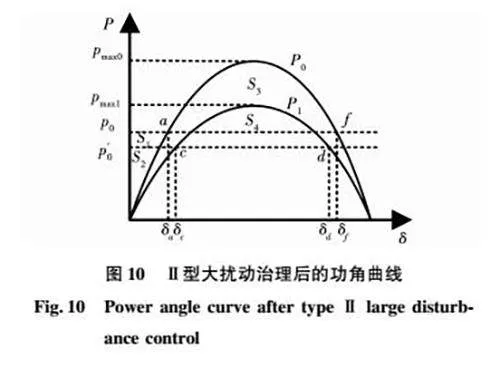
经本文所提出的控制策略治理后的VSG的功角曲线如图10中实线P1所示，c、d为对应的其平衡点和不平衡点，δc和δd为对应的功角，减速面积S4将大于加速面积S2。

对于Ⅱ型扰动发生的情况，在Simulink仿真模型运行的过程中，提取出的相位图如图11所示。在故障发生时刻前，不管是经过治理的VSG和没有经过治理的VSG，平衡点都是（δa，Δω=0）。在故障发生后，没有经过治理的VSG的功角和频率一直增大，直到超出最大临界点。然而，经过治理的VSG的频率和功角在经过一段时间波动以后，重新稳定在一个新的平衡点（δc，Δω=0）。

2.2.2 考虑切除故障

由于微电网的短路故障保护有一个快速反应时间，这个反应时间依赖于参数设置，同时也可能会与控制器及断路器的反应时间相关。因此，从短路故障发生到短路故障线路被切除会需要一定的时间才能完成。而且必须在越过不稳定平衡点之前，确保故障被切除。除此之外，在考虑切除故障情况下，可以利用扩展的等面积法则理论对暂态功角稳定性进行分析。

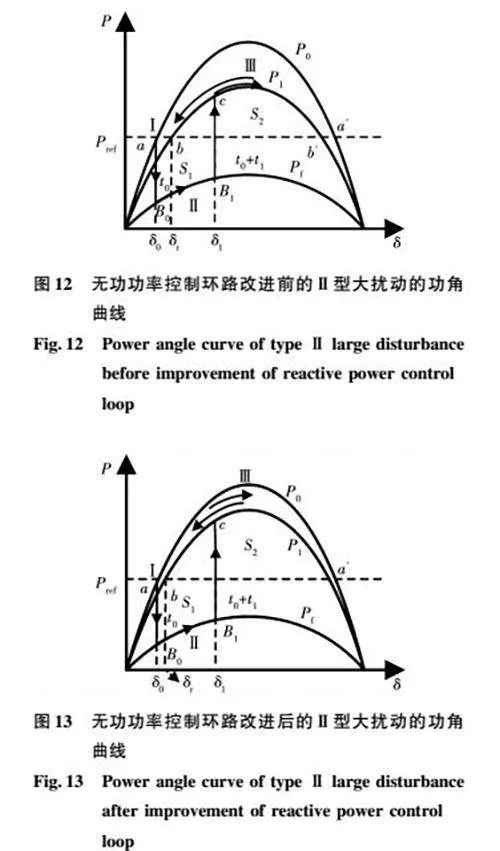
在考虑切除故障的情况下，Ⅱ型大扰动发生的整个物理过程按照时间顺序可以被分成第Ⅰ、Ⅱ及Ⅲ阶段，如图12所示。假设扰动发生在t0起始时刻，那么在t0时刻以前，VSG系统一直处于稳定运行状态，其中：a（δ0，Δω=0）点为稳定平衡点，a′（π-2φ-δ0，Δω=0）为不稳定平衡点，这一阶段被定义为第I阶段。在t0时刻发生大扰动，运行点从功角曲线P0上的点a下降到功角曲线Pf上的点B0。由于Prefgt;Pf，导致dω/dtgt;0，功率指令和功率输出表现为不平衡，频率和功率角开始增大，直到继电器动作切除故障线路。从大扰动发生到故障清除这一阶段被定义为第Ⅱ阶段。在t0+tf及以后时刻，故障被切除后，如果在无功功率环路不采用所提控制策略的情况下，由于双回线路变成单回线路，线路阻抗变大，PCC点电压回不到额定值。因此，功角曲线一般不会快速重新回到功角曲线P0，此时的功角曲线P1会低于功角曲线P0。此外，由于c点远离b点，在S2gt;S1的前提条件下，即减速区域面积大于加速区域面积，功角会经过一个动态振荡过程之后，最终稳定在b点。相反，如果无功功率控制环路采用所提控制策略，功角曲线则会提高，并且有希望快速重新回到P0。随着功角曲线被提高，加速面积减小，减速面积增大，更有利于功角稳定，如图13所示。

在第Ⅰ阶段，在t0时刻及以前，VSG系统以稳态运行情况下的虚拟阻抗Zs工作在稳定平衡点a，在平衡点a处，VSG的转动方程可以描述为

其中|Zs|和φs分别是稳定运行态运行状态下使用的虚拟阻抗的幅值和阻抗角。由于这一阶段的状态变量可以作为第Ⅱ阶段的初始条件。因此，根据式（13），平衡点a（δ0，Δω=0）处的功角δ0的表达式可写成如下形式：

同样，为保证平衡点的存在，稳定平衡点处的功角δ0必须满足如下条件：

在第Ⅱ阶段，在t0时刻至t0+t1时刻这一时间段内，由于电网三相短路故障会导致Vpcc的幅值瞬间大幅降低，无功功率控制环路来不及响应，如果虚拟阻抗仍然保持着Zs，则会出现非常大的电磁暂态电流。因此，需要确定限流虚拟阻抗的边界Zf。参照Ⅰ型扰动发生过程中限流阻抗边界的确定方法，限流阻抗边界条件如下：

在第Ⅲ阶段，由于第Ⅱ阶段的结束状态B1是第Ⅲ阶段的初始状态。在点B1处的状态变量，即功率角δ1和角频率偏差Δω1，可以通过使用锁相环测量获得，用于评估第Ⅲ阶段的暂态功角稳定性。当故障线路被切除后，Vpcc会快速恢复。假设恢复后的电压为Vpost，则转动方程可以用下式表示：

其中|Zr|和φr分别表示第Ⅲ阶段特定的虚拟阻抗幅值和阻抗角。

为了评估系统是否能再次实现渐近稳定，类似于前面对Ⅰ型大扰动的分析，采用了李雅普诺夫稳定性定理。如前所述，李雅普诺夫能量函数可以写成如下形式：

其中δr为电压恢复后的稳定平衡点对应的功角，可通过替换式（13）中的相关变量计算得到。

将这一阶段的不稳定平衡点（π-2φr-δr，Δω=0）和B1（δ1，Δω1）代入到式（28），可得到临界能量值Vcr和初始能量值V（δ1，Δω1）。然后，根据式（17）描述的李雅普诺夫稳定性标准，类似于式（19）的推导，最终可得到满足功角稳定性的虚拟阻抗边界，即

与文献[19]相比，本文的贡献在于经过研究发现，在无功功率控制环路的作用下，将电压指令值不再作为状态变量，而是作为参数变量处理，避免了重新构造李雅普诺夫函数。并且将I型扰动的虚拟阻抗优化模型扩展到了Ⅱ型扰动的不考虑切除故障类型当中。除此之外，将故障线路切除后，功角曲线降低的情况考虑其中。因此，本文的目的是通过虚拟阻抗优化对建立电压增量的自由控制支路的无功控制环路提供约束条件。

3 自适应电压和虚拟阻抗控制

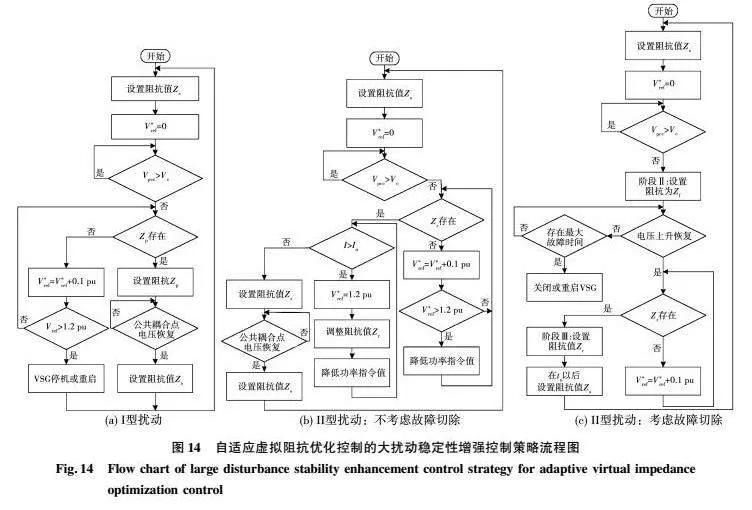
在不同的应用工况条件下，为了获得更好的动态性能，必须优化控制参数。为此，在上述理论分析的基础之上，提出一种自适应的虚拟阻抗和电压优化控制策略。首先，应当时刻检测公共耦合点电压，一旦出现电压值低于09 pu的情况，则会进入故障分类、处理阶段。如上所述，根据大扰动的类型Ⅰ和类型Ⅱ，将控制程序分为两种情况分别处理。为了区分这两种情况，应导出它们之间的临界电压边界Vc，如下式所示：

边界位于功率基准线与功率角曲线相切的位置，如图9所示。

如果Vpccgt;Vc，表示扰动属于I类大扰动，如图14（a）所示，则将从预先制作的查找表中选择大扰动期间的虚拟阻抗，该表由Zp表示。如果电网较弱，Zp可能会不存在，需要动态提高逆变器的电压指令值，电压指令值变化的步长不易过大或过小，步长过小则收敛速度变慢，步长过大会跨越最优动态电压值达到极限值，本文设定步长为01 pu，经过仿真验证实际可行。在提高电压指令后，需要重新判断Zp的存在，如果在电压达到极限的情况下Zp仍然不存在的情况下，应当关停VSG，待清除故障后重新开机。

如果Vpcclt;Vc，表示扰动属于Ⅱ类大干扰，如果故障不能够清除，如图14（b）所示，此时，应当通过提高逆变器的电压指令来恢复平衡点，在动态增加电压的过程中时刻检测Zr的存在。如果在电压达到极限的情况下Zr仍然不存在的情况下，则需要通过降低功率指令恢复平衡点，使得Zr恢复存在。如果出现过流，则应当调整Zr和降低功率指令值。如果故障可以被清除，如图 14（c）所示，则应该在每个阶段选择合适的虚拟阻抗。

4 仿真分析

为了验证本文当中所提的控制策略理论的准确性及可行性，搭建了完整的 VSG 单机无穷大并网系统 Simulink 仿真验证模型，在仿真模型当中所用到的主要部分参数如表 1 ～ 表 3 所示。"值得说明的是，本文没有考虑阻抗比对暂态功角稳定性的影响，将阻抗比取了一个定值。

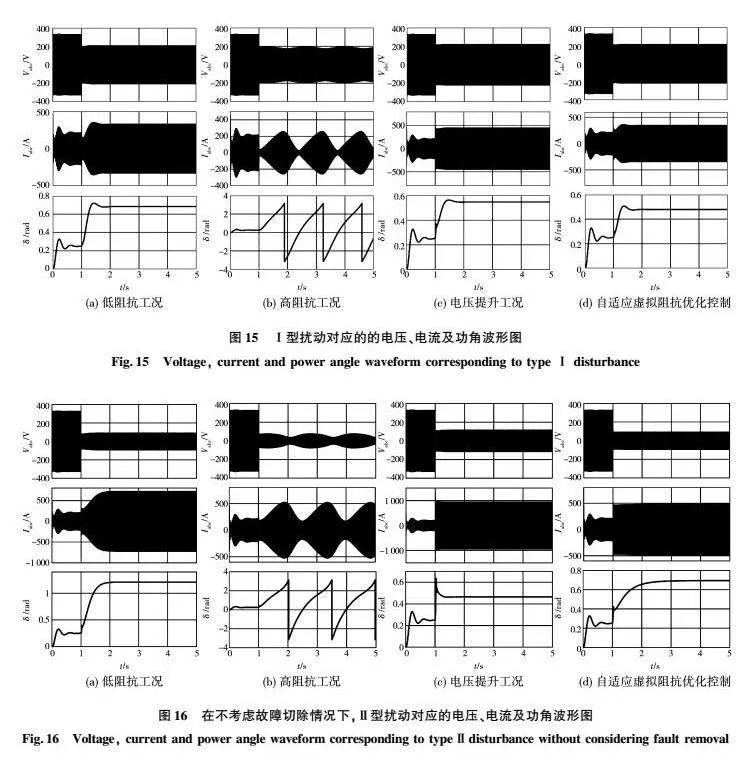
Ⅰ型大扰动对应的仿真结果如图15所示。其中，图15（a）显示的是在没有Vref作用下，低虚拟阻抗情况下的实验结果。在t=1 s的时候发生三相短路故障，此时电压跌落固定值值为04 pu。可以发现，在低虚拟阻抗条件下，功角保持稳定，并且电流峰值满足15IN的要求。证明了在I型扰动发生后，虚拟阻抗边界内重叠区域存在。然而，如图15（b）所示，随着虚拟阻抗值的增加，功角发生振荡。在Vref作用下，功角再次稳定，如图15（c）所示。通过对比图15（a）和图15（c）可以发现，Vref虽然使功角稳定，并且此时功角要小于低虚拟阻抗作用下的功角，但是电流却远大于低虚拟阻抗作用下的电流。在自适应电压和虚拟阻抗作用下，情况如图15（d）所示。通过对比图15（a）和图15（d）可以发现，此时两者电流大小几乎相同，然而，后者的功角要小于前者。因此，功角稳定性更好。对比图15（c）和图15（d），可以发现后者的电流幅值和功角都要好于前者。因此，低虚拟阻抗有利于功角稳定，但不利于限制电流。高虚拟阻抗有利于限制过流，但不利于功角稳定。主动调高电压指令可以提高功角稳定性，但是会出现过流问题。因此，在主动提高电压和虚拟阻抗优化的作用下，暂态功角稳定性和过流同时被优化。

对于Ⅱ型大扰动发生情况下，不考虑故障切除条件的仿真结果如图16所示。其中，图16（a）展示的是在没有Vref作用下，低虚拟阻抗情况下的实验结果。在t=1 s的时候发生三相短路故障，此时电压跌落值为08 pu。可以发现，在低虚拟阻抗条件下，功角保持稳定，电流峰值大于15IN。证明在Ⅱ型扰动发生后，虚拟阻抗边界内重叠区域不存在。随着虚拟阻抗值的增加，电流峰值降低，功角发生振荡，如图16（b）所示。在Vref作用下，功角再次稳定，如图16（c）所示。然而，同样通过对比图16（a）和图16（c）可以发现，Vref虽然使功角稳定，并且此时功角要小于低虚拟阻抗作用下的功角，但是电流却远大于低虚拟阻抗作用下的电流。在自适应电压和虚拟阻抗作用下的情况如图16（d）所示，通过对比图16（a）和图16（d），可以发现此时后者电流峰值小于前者，并且后者的功角也要小于前者。但是，尽管图16（d）有功参考值降低了50%，然而，VSG的输出电流仍然无法满足15IN的要求。因此，一方面可以进一步降低功率指令值，直至满足电流限制要求，另一方面如果功率区间满足2IN或更高，那么在故障不切除的情况下，VSG并网系统将保持与电网同步运行。

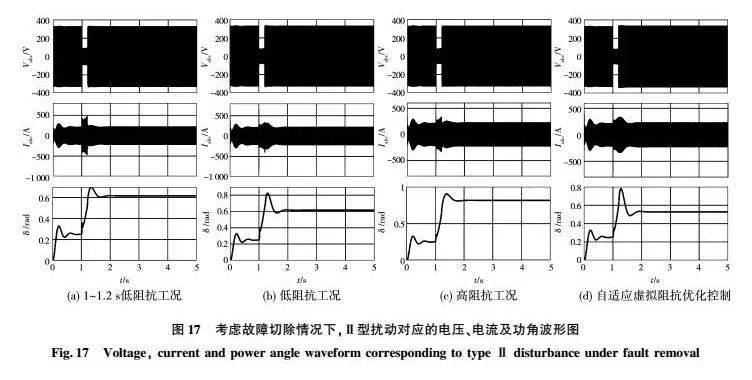
对于Ⅱ型大扰动发生情况下，考虑故障切除条件的仿真结果如图17所示。对比图17（a）和图17（b）可以得知，在1～12 s之间如果虚拟阻抗不满足Zf的要求，会导致VSG系统出现过电流。对比图17（b）和图17（c）可以得知，从双回线路切换成单回线路之后，由于虚拟阻抗增大，降低了功角的稳定裕度。对比图17（c）和图17（d）可以得知，在故障切除后主动提高电压指令值会提高功角的稳定裕度。

5 结 论

针对不同的运行工况，通过设置电压增量的自由控制支路可以有效提高暂态功角稳定性，然而，电压增量的设置需要约束条件。采用本文所提出的基于虚拟阻抗优化的自适应控制算法可以建立约束条件，在保证暂态功角稳定性的前提下，对过电流也可以起到明显的抑制作用。

通过设置电压增量的自由控制支路有助于解决在弱电网条件下，虚拟阻抗优化对提高暂态功角稳定性的局限性。因此，无功功率控制环路优化和虚拟阻抗优化对提高暂态功角稳定性可以起到相辅相成的作用。

参 考 文 献：

［1］"耿华， 何长军， 刘浴霜，等. 新能源电力系统的暂态同步稳定研究综述[J]. 高电压技术， 2022， 48（9）：3367.

GENG Hua， HE Changjun， LIU Yushuang， et al. Overview on transient synchronization stability of renewablerich power systems［J］. High Voltage Engineering， 2022， 48（9）： 3367.

［2］"ZHOU Jenny Z， DING Hui. Impact of short circuit ratio and phase locked loop parameters on the smallsignal behaviour of a VSCHVdc converter[C]//2016 IEEE Power and Energy Society General Meeting （PESGM）， July 17-21， 2016，Boston， MA， USA. 2016： 56.

［3］"HARNEFORS Lennart， BONGIORON Massimo， LUNDBERG Stenfan. Inputadmittance calculation and shaping for controlled voltagesource converters[J]. IEEE Transactions on Industrial Electronics， 2008， 54（6）：3323.

［4］"JIANGHAFNER Ying， MANCHEN Manfred. Stability enhancement and blackout prevention by VSC based HVDC[C]//CIGRE symposium， September 13-15， 2011， Bologna， Italy.2011：42.

［5］"WANG Xiongfei，HARNEFORS Lennart，FREDE Blaabjerg.Unified impedance model of gridconnected voltagesource converters[J].IEEE Transactions on Power Electronics，2018，33（2）：1775.

［6］"FU Xikun， SUN Jianjun， HUANG Meng， et al. Largesignal stability of gridforming and gridfollowing controls in voltage source converter： a comparative study[J].IEEE Transactions on Power Electronics，2021，36（7）：7832.

［7］"WU Heng， WANG Xiongfei. Designoriented transient stability analysis of gridconnected converters with power synchronization control[J]. IEEE Transactions on Industrial Electronics， 2019， 66（8）：6473.

［8］"SHUAI Zhikang， SHEN Chao， YIN Xin， et al. Fault analysis of inverterinterfaced distributed generators with different control schemes[J]. IEEE Transactions on Power Delivery， 2018，33（3）：1223.

［9］"HE Lili， SHUAI Zhikang， ZHANG Xin， et al. Transient characteristics of synchronverters subjected to asymmetric faults[J]. IEEE Transactions on Power Delivery， 2019，34（3）：1171.

［10］"ZHONG Qingchang， WEISS George. Synchronverters： inverters that mimic synchronous generators[J]. IEEE Transactions on Industrial Electronics， 2011， 58（4）：1259.

［11］"SHINTAI T， MIURA Y， ISE T.Oscillation damping of a distributed generator using a virtual synchronous generator[J]. IEEE Transactions on Power Delivery， 2014， 29（2）：668.

［12］"SHUAI Zhikang， HUANG Wen， SHEN Zheng John， et al. Active power oscillation and suppression techniques between two parallel synchronverters during load fluctuations[J]. IEEE Transactions on Power Electronics， 2020，35（4）：4127.

［13］"MENG Xin， LIU Jinjun， LIU Zeng.A generalized droop control for gridsupporting inverter based on comparison between traditional droop control and virtual synchronous generator control[J]. IEEE Transactions on Power Electronics， 2019， 34（6）：5416.

［14］"PAQUETTE Andrew D， DIVAN Deepak M.Virtual impedance current limiting for inverters in microgrids with synchronous generators[C]// Energy Conversion Congress and Exposition（ECCE），September 15-19，2013，Denver，CO，USA.2013：1039.

［15］"HUANG Linbin， XIN Huanhai， WANG Zhen， et al. Transient stability analysis and control design of droopcontrolled voltage source converters considering current limitation[J]. IEEE Transactions on Smart Grid， 2019， 10（1）：578.

［16］"LIU Teng， WANG Xiongfei.Transient stability of singleloop voltagemagnitude controlled gridforming converters[J]. IEEE Transactions on Power Electronics， 2021， 36（6）：6158.

［17］"SHUAI Zhikang， SHEN Chao， LIU Xuan， et al. Transient angle stability of virtual synchronous generators using Lyapunov’s direct method[J]. IEEE Transactions on Smart Grid， 2019， 10（4）：4648.

［18］"CHEN M， ZHOU D， BLAABJERG F. Enhanced transient angle stability control of gridforming converter based on virtual synchronous generator[J]. IEEE Transactions on Industrial Electronics， 2021， 69（9）： 9133.

［19］"LI Mingxuan， SHU Sirui， WANG Yue， et al. Analysis and improvement of largedisturbance stability for gridconnected VSG based on output impedance optimization[J]. IEEE Transactions on Power Electronics， 2022（8）：37.

［20］"ZHAO Feng， SHUAI Zhikang， HUANG Wen， et al. A unified model of voltagecontrolled inverter for transient angle stability analysis[J]. IEEE Transactions on Power Delivery， 2021， 37（3）： 2275.

［21］"QORIA T， GRUSON F， COLAS Fréderic， et al. Critical clearing time determination and enhancement of gridforming converters embedding virtual impedance as current limitation algorithm[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics， 2020，8（2）：1050.

［22］"SHUAI Zhikang， SHEN Chao， YIN Xin， et al. Fault analysis of inverterinterfaced distributed generators with different control schemes[J]. IEEE Transactions on Power Delivery， 2018，33（3）：1223.

［23］"张余余， 赵晋斌， 李芬，等. 基于功角动态补偿的VSG故障穿越方法研究[J]. 电网技术， 2021，45（9）：3667.

ZHANG Yuyu， ZHAO Jinbin， LI Fen， et al. VSG fault crossing method based on dynamic compensation of power angle［J］. Power System Technology，2021，45（9）： 3667.

［24］"MACHOWSKI J. Power system dynamics—stability and control[M]. New York：Wiley，2008.

［25］"SASAKI H. An approximate incorporation of field flux decay into transient stability analyses of multimachine power systems by the second method of Lyapunov[J]. IEEE Transactions on Power Apparatus and Systems， 1979， 98（2）：473.

［26］"KHALIL H. Nonlinear systems englewood cliffs[M]. NJ， USA：PrenticeHall， 1996.

［27］"葛平娟， 涂春鸣， 肖凡，等. 面向暂态稳定性能提升的VSG参数灵活控制策略[J]. 中国电机工程学报， 2022， 42（6）：2109.

GE Pingjuan， TU Chunming， XIAO Fan， et al. Transient stability enhancement of a VSG based on flexible switching of control parameters［J］. Proceedings of the CSEE， 2022， 42（6）： 2109.

［28］"JIN Zheming， WANG Xiongfei. A DQframe asymmetrical virtual impedance control for enhancing transient stability of gridforming inverters[J]. IEEE Transactions on Power Electronics， 2022， 37（4）： 4535.

［29］"唐英杰， 查晓明， 田震， 等. 弱电网条件下虚拟同步机与SVG并联系统的暂态稳定性分析[J]. 电网技术， 2022， 46（10）：4020.

TANG Yingjie， ZHA Xiaoming， TIAN Zhen， et al. Transient stability analysis of virtual synchronous generator and SVG parallel system under weak grid conditions［J］. Power System Technology， 2022， 46（10）： 4020.

［30］"XIONG Xiaoling， WU Chao， PAN Donghua， et al. An improved synchronization stability method of virtual synchronous generators based on frequency feedforward on reactive power control loop[J].IEEE Transactions on Power Electronics，2021，36（8）：9136.

［31］"宋丹，张武洋，王成华.含光储系统的微电网能量协调控制策略［J］.哈尔滨理工大学学报， 2021， 26（6）： 94.

SONG Dan， ZHANG Wuyang， WANG Chenghua. Coordinated control strategy of microgrid energy with optical storage system［J］. Journal of Harbin University of Science and Technology， 2021， 26（6）： 94.

［32］"全少理，朴哲勇，陈鹏浩，等.光伏系统自适应光照和局部遮光的MPPT跟踪[J].哈尔滨理工大学学报，2020，25（6）：53.

QUAN Shaoli， PIAO Zheyong， CHEN Penghao， et al. MPPT tracking of adaptive lighting and partial shading in photovoltaic systems［J］. Journal of Harbin University of Science and Technology， 2020， 25（6）： 53.

（编辑：刘琳琳）

收稿日期： 2023-04-13

基金项目：国家自然科学基金（U21A20145）；中国博士后科学基金（2021M701018）

作者简介：孙久亮（1991—），男，博士研究生，研究方向为新能源发电及其并网稳定性控制；

蔡 蔚（1959—），男，博士，教授，博士生导师，研究方向为驱动电机、功率电子控制器及汽车电动化电驱动系统、低振动噪声电机等；

郭庆波（1987—），男，博士，研究方向为新能源汽车电机驱动器控制、绕组切换、电机优化设计。

通信作者：蔡 蔚