2023年全国高考乙卷理综第25题的评析与思考

摘 要：2023年全国乙卷理综第25题为物理压轴题，综合性强、运动过程复杂、难度大，突出体现了对学生必备知识、关键能力和综合素质的考查.本文从命题意图、试题释疑、试题解评、教学思考等方面进行探讨.

关键词：弹性碰撞；试题评析；教学思考

中图分类号：G632   文献标识码：A   文章编号：1008-0333（2024）01-0100-03

收稿日期：2023-10-05

作者简介：邓伟（1976.1-），男，中学高级教师，从事试题与教学实践研究.

2023年高考全国理综乙卷物理试题全面落实教育立德树人的根本任务.加强教考衔接，遵循课程标准，依托中国高考评价体系，注重深化物理基础；增强探究性，突出科学思维考查和科学素养考查，注重物理方法的培养，引导教学注重作业题、训练题减量提质，减少“重复、机械刷题”，促使教学把教材内容讲全讲透，提升课堂效果，形成学生必备知识与关键能力.而高考压轴题作为一份试卷的精华所在，也是高考命题的风向标，最能体现高考的命题意图和思想.试题分析就是一线教师与命题者的间接“对话”，应充分理解考题的设计意图，从而对高中物理教学发挥更加明确的导向作用.

1 原题重现

（2023年全国乙卷理综第25题）如图1所示，一竖直固定的长直圆管内有一质量为M的静止薄圆盘，圆盘与管的上端口距离为l，圆管长度为20l.一质量为m=13M的小球从管的上端口由静止下落，并撞在圆盘中心，圆盘向下滑动，所受滑动摩擦力与其所受重力大小相等.小球在管内运动时与管壁不接触，圆盘始终水平，小球与圆盘发生的碰撞均为弹性碰撞且碰撞时间极短.不计空气阻力，重力加速度大小为g.求：

（1）第一次碰撞后瞬间小球和圆盘的速度大小；

（2）在第一次碰撞到第二次碰撞之间，小球与圆盘间的最远距离；

（3）圆盘在管内运动过程中，小球与圆盘碰撞的次数.

2 试题评析

2.1 命题意图

落实物理学科核心素养是2023年全国乙卷理综第25题命题的最大亮点，物理观念和科学思维是物理学科核心素养的重要组成部分.培养学生的物理观念，决定着学生对物理知识理解的深入度和应用的灵活性，对学生终生的学习和发展具有重要作用；培养学生的科学思维，让学生能够对模型建构、科学推理、科学论证、质疑创新等要素和科学思维方法有机整合.本题直观考查了弹性碰撞相关知识，深入考查了物理观念中的物质观、运动观、能量观和科学思维中的模型建构、科学推理等核心素养的重要方面.在熟悉的情景中，注重考查了学生是否具有独立思考、分析问题和灵活解决问题的科学思维能力.引导物理课堂应跳出题海战术，树立学生正确的思维方式，提高学生物理学科核心素养，为学生的终生发展奠基.

2.2 试题释疑

本题的疑点是第（3）问.小球反复地追击圆盘并发生弹性碰撞，体现在运动过程复杂、多次弹性碰撞的计算难度大，用常规的分段分析的方法解答，耗时多，因此对思维方法、规律把握、解题方法和计算要求较高.因此，突破疑点应抓以下几个方面：第一，除碰撞瞬间，小球做加速度为g的匀变速直线运动，圆盘做对应阶段的匀速运动；第二，受限条件是管的总长度20l，但注意圆盘初始位置离上管口为l，可以通过圆盘向下运动的位移与这一条件建立联系；第三，圆盘运动中受力平衡，小球在管中下降减少的重力势能转化为小球、圆盘的动能；第四，每相邻两次碰撞的时间相同，每次碰撞前后瞬间小球、圆盘的相对速度大小相等，方向相反，即深度掌握和熟练应用弹性碰撞规律.

2.3 试题解析

分析 第（1）问体现了基础性，考查了匀变速直线运动（自由落体）和典型碰撞模型弹性碰撞，突显物理学科核心素养中的运动观与模型建构能力.本问物理情景、运动规律学生较熟悉，解答方法较多，比较容易.学生存在的问题是对“一动一静”式弹性碰撞的方程不会解或没有记住碰撞后的速度关系.

（2）类比成追击相遇问题，利用v-t图像求解.

分析 第（2）问在第（1）的基础上，由单一物体的运动变成两个物体的运动，除了运动与碰撞外，还增加圆盘的受力平衡，难度加大.结合（1）问碰撞后的速度和圆盘的受力情况，也较为容易分析出小球和圆盘的运动情况.解答的方法较多，应用v-t图像求解简便、省时.学生存在的问题是第（1）问的速度没有算出，无法进行后续分析.

（3）本问是本题的分水岭，采用多种方法求解.

解法1 常规解法，分段分析

解法2 归纳法与能量的结合

解法3 利用v-t图像

分析 第（3）问综合难度大，小球反复地追击圆盘并发生弹性碰撞，运动过程复杂、多次弹性碰撞的计算难度大.这就要求学生真正理解弹性碰撞的特点，同时全局把握小球、圆盘的运动规律、能量转化情况，从而选择合适的解题方法.解法1是大多数学生都能想到的，但解答过程复杂、耗时多，不能完整解答；解法2从整体上分析得出碰撞后瞬间小球、圆盘的速度“通项式”和能量转化关系，解答较为容易，但学生不易想到；解法3利用v-t图像，解法简洁直观、思路清晰、运算简单，解答效率更高，且运动学图像也是学生较熟悉的，但不少学生不习惯利用图像辅助解题［1］.学生存在的问题是本问综合性强、难度大，物理过程分析不清，甚至较多学生无时间分析而放弃.

3 教学思考

3.1 解题思维障碍分析

物理教学过程是引导学生进行观察、分析、解决问题的过程.然而，在教学过程中，时有学生反映如下问题：（1）课堂上讲的内容能够理解，但是再次碰上相同或者相似模型时，却感到熟悉又无奈；（2）刷了很多习题，但是解题过程依然处处碰壁；（3）解题过程中认为思路是对的，结果发现解答不下去，半途而废.以上反映在多次弹性碰撞类问题中更为突出.说明学生并没有从学习活动中获取解决问题的关键能力，主要表现在套用模型导致解题思路固化的思维障碍. 在学习构建模型过程中，很多学生选择把模型记住，在解题過程中直接把记忆中的模型和对应的规律进行复述.而实际问题的情境是多变的，所需要构建的模型也是相应变化的，应用的规律、解题的方法也随之而变，因此学生的思维在此处脱节，造成了思维上的障碍.这说明学生对模型的分析不够深入，对规律不能类化、迁移，从而影响解题.

3.2 思维障碍突破策略

随着新高考的不断深化，必须正视高考对教学的引导功能.如果教师还只停留在教给学生知识，而不注重学生分析问题和解决问题能力的提升、解答方法的引导，稍为灵活的试题或压轴题就会成为多数学生的分水岭.在2023年全国乙卷理综第25题第（3）问中，学生能够感受到弹性碰撞模型很熟悉，想法可能也很多，但却无法有效解决问题，熟悉的模型变得不再熟悉［2］.

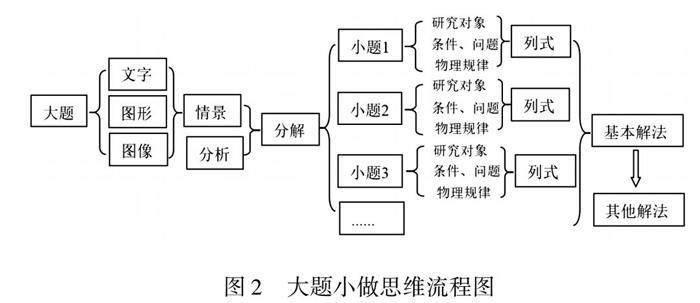
因此，物理学科的规律不是套路，解题过程更不能生搬硬套，而是要把握解决问题的规律.其中模型、条件可以根据实际情境千变万化，但是解题的规律却是相对稳定的，分析透物理规律，才能选择灵活的解法.如何利用学科关键能力解决物理问题是教学中的重要目标，可以把每个综合问题（大题）都可分解为多个小问题（小题），即采用“大题小做”的问题解决模式（如图2），对问题的分析将更具有可行性.

以本题为例.此问涉及多对象、多阶段、多规律的复杂运动，学生看完问题后思维容易混乱.若采用大題小做的问题解决模式，本题的思路就比较清晰了.如小题1，小球做自由落体运动，列匀变速直线运动方程；小题2，小球与圆盘发生弹性碰撞，列动量守恒和动能守恒方程；小题3，由小题2的结果可得小球做竖直上抛运动，圆盘受力平衡做匀速直线运动，类似追击相遇问题，小球先向上减速然后向下加速追上圆盘并发生第二次碰撞，列小球、圆盘位移相等方程、匀变速直线运动速度关系，弹性碰撞动量守恒、动能守恒方程；小题4，小球第二次碰撞后瞬间的速度为0，做自由落体运动，圆盘以第二次碰撞后瞬间的速度做向下匀速直线运动.小球追上圆盘发生第三次弹性碰撞，列式与小题3相似；再续分小题，分析思路与小题3、4类似，这就是基本解法.通过基本解法中碰撞前后小球、圆盘的速度关系分析，能量情况分析，可以灵活选择其他解法.

4 结束语

高考试题是经过命题专家深思熟虑的结果，经典模型［3］不按“套路”出牌，常考常新是高考试题的亮点.通过对2023年全国高考乙卷理综第25题分析，可以看出试题以经典的弹性碰撞模型为基础，通过受力分析、运动情况分析、能量角度的思考，考查综合分析能力、情景类比迁移能力、计算能力、识图作图能力等，充分落实物理学科核心素养中的物理观念和科学思维中的运动观、能量观、模型建构等方面能力要求.虽然本题物理模型、情景熟悉，但是却对学生必备知识、关键能力的要求很高，需要学生能够灵活分析，巧妙解答.这就要求教师在课堂教学中既要立足于基础，即立足于物理的基本概念、基本规律、基本方法和基本技能，又要重视思维方法的引导、拓展，解题方法的训练与提升.高考注重能力的考查，实际上是考查学生对基本知识、基本技能的理解、掌握和结合实际的灵活运用.对待基础知识，一应理解和应用，二应注重归纳与建构，三应综合与迁移，落实学科关键能力的培养.

参考文献：

［1］ 张其林.巧用数形结合 助力物理解题［J］.中学物理，2022（1）：51-52.

［2］ 曹芳.深耕教材 强化主干 提升素养［J］.物理教学，2022（9）：57-59.

［3］ 李恒林.抓住题眼巧建模 科学推理真收获［J］.物理教师，2022（11）：87-89.

［责任编辑：李 璟］