基于“理解”的“余弦定理”课堂教学实践

⦿ 江苏省姜堰第二中学 陆婧婧

在数学学习中,若想灵活应用数学知识解决问题,首先就要理解它,只有理解了才能更深刻地感觉它、应用它.不过,受唯分论的影响,部分教师为了追求“速度”,常常以灌输的方式教学,学生因为没有经历独立思考和自主探究的过程而未能理解知识的本质和内涵,这样灵活应用自然无从谈起.在日常教学中,教师要重视引导学生经历知识的探索过程,充分激发学生的主体性和积极性,从而让学生获得真正的理解,提高学生数学学习水平.

1 挖掘“理解”的数学教学内涵

在数学教学中,教师要重视引导学生挖掘知识的本源,揭示问题的本质,提炼蕴含其中的数学思想方法,从而让学生真正地理解知识.基于此,教师要打破“讲授式”教学模式的束缚,提供时间和机会让学生自主探究,并通过课堂教学激活学生的数学思维,让学生用数学的思维去思考,用数学的语言去表达,从而让学生对知识的认识理解逐渐走向深入,最终形成数学知识.

在日常教学中,若想让学生对知识达到理解的程度,教师要以客观材料为媒介,让学生将新知与旧知有效地联系起来,引导学生经历探究新知的全过程,让学生充分体会知识的实用性、必要性,促进学生知识体系的建构和完善.在此过程中,教师不仅要教授知识,更要传递、渗透蕴含其中的思想方法和经验,帮助学生理解问题的本质和内涵,提高学生灵活运用知识解决问题的能力,提升学生数学素养.

2 渗透“理解”的课堂教学实践

在“余弦定理”教学中,教师以学生已有知识和经验为出发点,基于学生基本学情创设符合学生认知水平的探究活动,让学生主动参与到新知识的教学实践中,让学生通过经历思考、探索、感悟等活动,真正地理解知识,提高数学能力和素养.教学设计如下：

2.1 情境引入,感悟新知

情境问题：小明周末从家出发购买学习用品和水果,他先是直线行驶300 m到文具店购买学习用品,然后直线行驶400 m去水果店购买水果.如图1,点A代表小明家,点C代表文具店,点B代表水果店,若CA与CB的夹角是60°,小明买好水果后直接直线行驶回家,你知道小明需要行驶多远的距离吗?

图1

问题给出后,教师启发学生将这一生活中常见的问题转化为数学问题：在△ABC中,已知AC=300,BC=400,∠C=60°,求AB的长.

设计意图：以学生熟悉的现实生活情境为背景,让学生感知数学在现实生活中的应用,激发学生探究欲,提高学生解决问题的能力.在此过程中,教师鼓励学生将问题向数学化转化,让学生深刻感受数学知识的简洁性、便捷性和必要性,为接下来的新知学习打下坚实的基础.

2.2 探究新知,促进理解

为了更加清晰地展示小明直线行驶的路径,教师启发学生利用箭头表示,学生给出图2所示的图形.

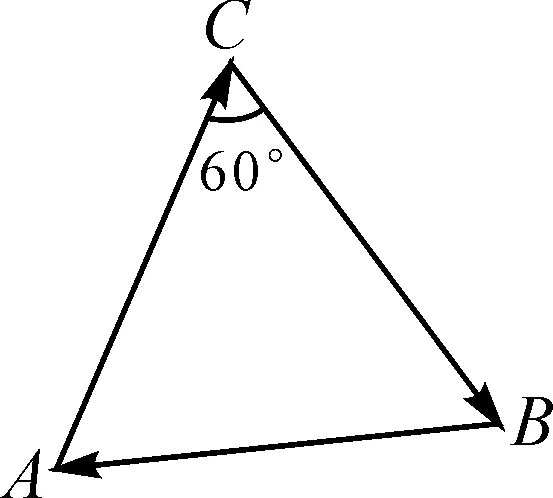
图2

师：观察图2,你想到了什么?(学生一时不知从何说起.)

师：如果从平面向量的角度来看,你能将以上情境转化为一道数学题吗?

师：非常好!根据图2的路径图,结合向量加法的学习经验,你能得到怎样的等式?

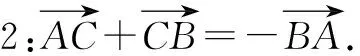
师：哪个小组说一说,你们是如何求解的?

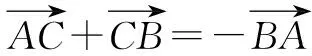
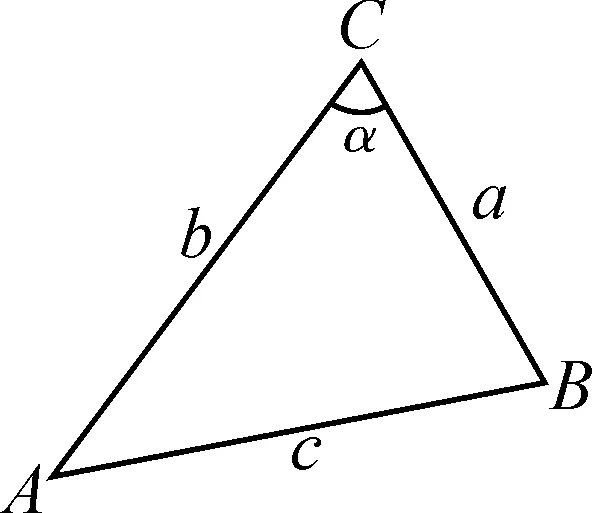
图3

(问题给出后,学生开始新一轮的探究.)

生5：结合以上探究过程,易得b2-2abcosα+a2=c2,即c2=b2-2abcosα+a2.

师：很好,结合“c2=b2-2abcosα+a2”这一关系式,我们可以研究什么问题?

生6：已知三角形两条边的长度分别为a和b,且两条边的夹角为α,则第三边的长度c可求.

师：很好,这就是我们今天所要学习的余弦定理.在△ABC中,若∠A,∠B,∠C所对应的边为a,b,c,你能得到怎样的数量关系?

生7：c2=a2+b2-2abcosC,a2=b2+c2-2bccosA,b2=a2+c2-2accosB.

师：非常棒,有了公式的帮忙,我们就能轻松地计算出小明从水果店到家的距离.

设计意图：在探究过程中,教师继续引导学生对问题进行抽象,并鼓励学生用向量的知识解决问题,以此借助已有经验有效沟通新知与旧知的联系,唤醒学生的原认知,让学生充分感知数学知识之间的内在联系,以便将新知纳入到原有的向量相关的知识体系中,促进个体知识体系的建构与完善.教师将主动权交给学生,通过有效问题的引领让学生经历数学化的过程,并通过由特殊到一般的转化,形成新知识.这样让学生亲历探索新知、抽象新知等过程,有利于促成学生对新知的深度理解,切实提高教学有效性.

2.3 巩固练习,加深理解

例1在△ABC中,已知a=5,b=4,∠C=120°,求c.

例3如图4,已知直线AB和CD相交于点O,且∠COA=80°.甲、乙两人同时从点O出发,分别沿OA,OC方向行驶,其步行速度分别为4 km/h和4.5 km/h,问3小时后,两人相距多远?(精确到0.1 km.)

图4

例3是一个以现实生活为背景的应用题,不妨设3小时后,甲到达点P,乙到达点Q,则问题可以转化为：在△OPQ中,已知OP=12 km,OQ=13.5 km,∠POQ=80°,求QP的长.

设计意图：通过基础练习,学生能从不同角度理解余弦定理.对于例1,已知三角形的两边和它们的夹角,可以求第三边;对于例2,已知三角形的三条边,可以求出角;对于例3,通过经历生活情境数学化的过程,进一步感知余弦定理的应用价值,真正实现为用而学,在学中用,学而能用.

2.4 课堂小结,升华认知

师：通过以上研究过程,你学到了哪些知识、方法?谈谈你的心得体会.

此环节先由学生归纳总结,然后师生共同完善.

设计意图：教师提供时间让学生思考“为什么学、学什么、怎么学”等问题,让学生脑海中形成清晰的知识脉络,达成真正的理解.

3 结束语

在高中数学教学中,教师作为课堂教学的组织者、引导者、启发者、点拨者,切勿将知识直接灌输给学生,应该创造机会让学生主动参与到新知识的学习实践中,引导学生深刻体会学习新知识的重要性与便捷性,激发学生学习的主动性和积极性,感悟“学以致用”的教学真谛.在学习新知识的过程中,要引导学生关注新知识与旧知识之间的内在联系,引导学生用旧知识去探索新知识,从而让新知识的学习更加自然、顺畅,更易于学生理解和接受,逐步提高学生自主探究能力,提升学生数学素养.

总之,在高中数学教学中,教师要不断提升自身的教学素质,认真地研究教学内容、研究学生,基于学生最近发现区创设有效的问题,提供机会让学生主动探索新知,充分发挥课堂教学的育人功能,让学生理解知识的本质与内涵,促进深度学习教学目标的落实.