高考数学“概率与统计”试题的特点及其教学启示

⦿ 长江大学信息与数学学院 罗 毅 李 勇

1 背景

“概率与统计”是高中数学四大主要课程之一.而高考中“概率与统计”试题形式多变,考查的侧重点和综合难度都有一定的变化,部分一线教师难以把握高考复习方向[1],因此对全国卷(全国甲卷、乙卷,新高考Ⅰ卷、Ⅱ卷)中“概率与统计”的相关试题进行统计分析,为教学实践提供有效的建议,提醒教师重视“概率与统计”内容[2].为教师开展有效的教学活动提供方向,充分发挥新高考在数学学科教育中的导向作用,以达到更好的教学效果.

2 研究方法

本文对2021年和2022年全国高考数学卷(理科)中的“概率与统计”试题进行统计分析(8套共计34个题目).考虑到不同题型所考查的内容和重点存在差异,因此将“概率与统计”试题分为选填题和解答题两大类,采用定性和定量相结合的研究方法,先对试题的命题特点进行统计分析,再从不同类型试卷入手,研究试题的综合难度,结合统计图表分析试题特点及试题综合难度.

2.1 命题特点分析

(1)情境领域：数学问题通常是以问题情境有机地展现出来.本文将依据新课标中情境的划分进行统计(现实情境、数学情境、科学情境三个维度).

(2)知识点：鉴于高考具有连续性、稳定性等特点,本文参考2019年高考考试大纲,对“概率与统计”考点进行分类和编码.

(3)数学核心素养：培养学生的数学核心素养,可以使他们在今后的数学学习中有更多独到见解,从而有利于他们的身心发展.本文将参照新课标结合数学核心素养的划分维度(数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析)对2021年和2022年高考数学“概率与统计”试题进行统计分析.

2.2 综合难度分析

综合难度分析可以把握试题的难易程度,并科学调控试题难度,从而提高命题质量.国内学者鲍建生[3]则根据我国数学课程的具体情况提出了五个难度影响因素的难度模型.本文将采用武小鹏等[4]基于AHP理论构建的研究数学高考试题综合难度模型,该模型含7个要素(背景因素、是否含参、运算水平、推理能力、知识含量、思维方向、认知水平),各要素又依据自身特点划分为不同水平,具体如表1所示.

表1 难度因素水平划分及内涵

3 数据统计与分析

3.1 试题特点分析

(1)情境领域分析

通过统计(见表2)发现,试题对现实情境的设置最多,如2021年全国乙卷第6题：“将5名北京冬奥会志愿者分配到花样滑冰等4个项目进行培训,……,则不同的分配方案共有多少种?”试题情境贴近现实生活,与国家时事紧密相联,培养学生的国家荣誉感和社会责任感,让学生充分体会数学知识的实用性,将理论和实践相结合.

表2 试题情境统计表

(2)知识点分析

2021年和2022年选填题在知识点上重点考查了“古典概型”“概率”以及“用样本估计总体”部分,其知识点含量的设计往往趋向单个知识点的考查,总体来说考查难度不大.而解答题对于“随机抽样”和“概率”知识点的考查最多,很少涉及“变量的相关性”和“随机数与几何概型”的考查;每道解答题所考查的知识点均在两个及两个以上,体现了知识点的融合性,突显出解答题设置的综合性.(知识点统计见表3.)

表3 知识点统计表

(3)数学核心素养分析

选填题着重考查学生的数学运算能力,注重数据分析能力,其命题符合考纲要求,具有实用性.解答题侧重数学运算、逻辑推理以及数学建模的考查,重视学生分析问题、解决问题能力的培养.以2022年新高考Ⅱ卷第19题为例,学生要从疾病与年龄间的关系情境中抽象出概率的数学问题,通过逻辑推理计算出患病平均年龄,并在此基础上建立模型计算某年龄段的患病率.(数学核心素养统计见表4.)

表4 数学核心素养统计表

3.2 试题综合难度分析

按照表1中不同因素的界定,对8套试卷中“概率与统计”试题进行分类赋值.具体如下：

例1(2022年全国甲卷第2题)某社区通过公益讲座以普及社区居民的垃圾分类知识,为了解讲座效果,随机抽取10位社区居民,让他们在讲座前和讲座后回答一份垃圾分类知识问卷,这10位社区居民在讲座前和讲座后问卷答题的正确率如图1：

图1

则( ).

A.讲座前问卷答题的正确率的中位数小于70%

B.讲座后问卷答题的正确率的平均数大于85%

C.讲座前问卷答题的正确率的标准差小于讲座后正确率的标准差

D.讲座后问卷答题的正确率的极差大于讲座前正确率的极差

分析：该试题难度水平及赋值——生活背景2;简单符号运算3;简单推理1(包含三步：一是通过散点图对数据进行排序;二是根据中位数概念找出中位数;三是根据平均数、标准差以及极差的计算公式分别计算出平均数、标准差以及极差);无参数1;知识点含量中等2;顺向思维1;运用认知水平2.

对2021年和2022年全国高考“概率与统计”知识单元涉及的34道试题同上进行分类和赋值,得到原始编码数据后根据综合难度系数公式进行计算,得到表5.

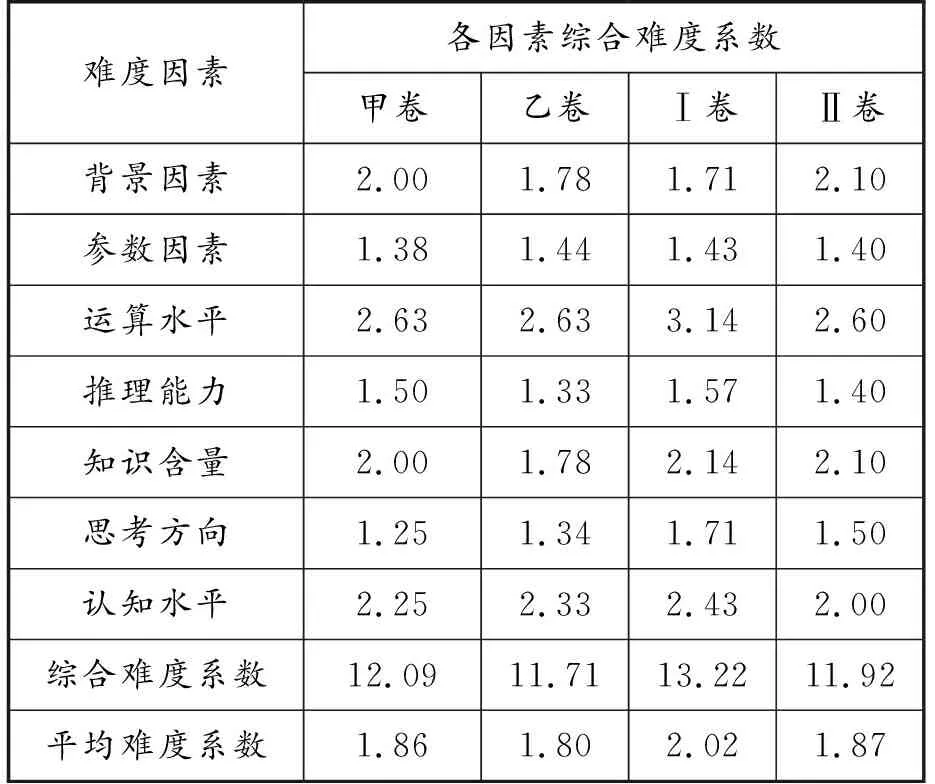
表5 综合难度系数

从整体来看,2021年和2022年高考数学全国卷中“概率与统计”试题的综合难度系数差距不大,其中新高考Ⅰ卷“概率与统计”试题的综合难度系数最高,达到13.22,甲卷、乙卷和新高考Ⅱ卷的综合难度相差不大,难度系数在12左右.

为直观了解2021年和2022年“概率与统计”试题在这7个维度上的侧重程度,绘出雷达图,如图2.

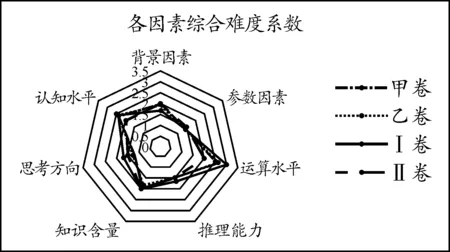
图2 综合难度系数雷达图

可见,2021年和2022年甲、乙卷以及新高考Ⅰ、Ⅱ卷在推理能力、参数因素、背景因素三个维度上的考查难度差异不大,难度水平基本相当.在运算水平、知识的认知水平和思考方向三个方面,新高考Ⅰ卷“概率与统计”试题的难度明显高于其他三卷,而在背景因素上又明显低于其他三卷;在知识含量方面,乙卷“概率与统计”试题的难度低于其他三卷;同时四种类型的试卷都重视对运算能力的考查,对此维度的考查力度远大于其他维度.

4 启示与建议

通过综合统计和分析,发现这一部分的试题具有以下特征：一是问题情境多以现实情境为主,具有现实性;二是试题涵盖的知识点广泛,内容丰富;三是各类型试题对学生数学核心素养考查的侧重点不同,具有针对性;四是不同试卷的试题综合难度相差不大,具有一致性.本文认为,随着信息时代的到来,“概率与统计”的概念逐渐被人们所关注,这不仅有利于转变学生的思维方式,也有利于培养学生的良好素质,也为培养大量的信息技术人才打下了坚实的基础.因此给出如下几点建议.

(1)问题情境方面

适当的问题情境是检验数学学科核心素养的一个重要载体.因此在命制试题时要充分考虑学生和社会的需求以及时代背景,创设更加合理的问题情境,充分体现试题的应用性,使学生了解到,数学是从生活中产生的,也是在生活中得到运用的.

(2)知识点方面

单一的知识点不能够体现高考试题综合性的特点,命题可以适当增加知识点的容量或渗透其他学科知识点,从而增加试题的综合性,帮助学生建立完整的知识框架.

(3)解题思维方面

命题时可以适当增加逆向思维的试题,如增加一些需用反证法、举反例、逆用定理等求解的题目,这样才能有效地提高学生的思维能力,培养他们的逆向思维,提高他们的解题能力.

(4)综合难度方面

为了保证试题的价值,并发挥试题的选拔功能和导向作用,命题人要考虑各难度因素的平衡性,研究课标、回归教材,秉持促进学生均衡且全面发展的理念,并根据不同地区对高考试题的要求,科学地去均衡各难度因素,提高试题的价值.