“概率统计”的复习备考建议

⦿ 广东省河源市东源县广州大学附属东江中学 张 雷

概率统计(含计数原理、排列组合与二项式定理等)模块知识是新高考数学试卷中的一个重要考查知识点,往往以“一大一小”(一个解答题,一个选择题或填空题)的形式来全面考查.此模块知识重在培养学生的阅读理解能力、理性数学思维方式以及解决问题的基本能力等.

在高中数学课程体系中,概率统计模块知识贯穿于必修、选择性必修课程之中,成为高中数学中的一个重要主题,也是全面培养与提升学生数学学科核心素养、发展创新意识与应用意识等方面的重要媒介之一.

特别地,在新教材、新课程、新高考的“三新”背景下,随着课程改革的不断深入,高考命题的创新引领,概率统计模块知识必将成为高考数学试卷中的核心知识和热点考点之一.鉴于此,结合概率统计模块自身的特点,高三复习备考中可以从以下一些细节与注意点入手,抛砖引玉,强化复习,提升能力.

1 重视数学阅读能力与理解能力的培养

概率统计模块知识的考查成为新高考创新命题的一个亮点,特别是涉及命题的“反套路”理念,以及学生“四能”的全面提升等方面的考查,成为高考命题中的一个新思路与新方式.

概率统计模块知识的考查往往依托现实生活中的阅读材料加以展开与考查,没有“套路”可循,这就对复习备考提出更高的要求,要求更加重视材料的阅读与理解能力,对于新的问题应用情境中的信息收集、信息加工与实际应用等提出更高的要求,要求教师要在平时的复习备考过程中,更加有针对性地进行这方面的训练,提升阅读理解能力等.

而对于很多学生得分情况不理想,甚至谈起概率与统计解答题便产生恐惧心理,就需要更有针对性地进行数学阅读理解能力的培养,借助应用场景与阅读材料,增强材料的信息加工,文字语言与符号语言的相互转化等方面的能力.

例1位于成都市龙泉驿区的东安湖体育公园是第31届世界大学生夏季运动会的核心场馆,它包含一座综合运动场、一座多功能体育馆、一座游泳跳水馆和一座综合小球馆.现安排包含甲、乙在内的6名同学到这4个场馆做志愿者,每人去1个场馆,每个场馆至少安排1个人,则甲、乙两人安排在相同场馆的方法种数为( ).

A.96 B.144 C.240 D.360

解析：首先将6名同学分成4组.一种方式是甲、乙组成一组,再从另外4人任选2人组成一组,其余的一人一组;另一种方式是甲、乙与另外4人中的1人组成一组,其余的一人一组.然后再把4组人分到4个场馆.

点评：此类涉及应用的计数问题,关键在于阅读理解能力,根据志愿者活动安排,通过分组的分类讨论,结合排列组合的相关知识进行简单的计数与应用,进而确定相应的安排方法种数.

2 重视数学基本概念和基本公式的理解

在数学复习备考过程中,对于概率统计模块知识,要更加重视对数学教材的回归与使用,真正起到数学教材的引领与指向功能.

在回归教材与应用教材过程中,结合概率统计模块知识的基本特点,要特别重视概率与统计中相关的基本概念的理解,以及一些相关基本公式的理解与掌握,把握解题的“通性通法”.特别要注意新教材中涉及全概率公式的应用等,并能熟练利用基本概念与基本公式来解决一些相关的应用问题,体现概念与公式的充分理解与把握等.

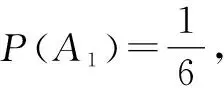
又利用对立事件的概率公式,可得

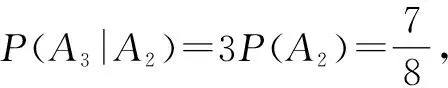
点评：该综合应用问题以概率为问题场景,通过条件概率以及递推关系式的合理交汇与综合,综合对立事件的概率公式以及全概率公式等来综合与应用,实现问题的巧妙分析与解决.特别要注意的是,合理利用事件概率之间的递推关系式,要注意后继事件的概率往往受前一个事件的概率的影响,需要逐一分析与求解,这对应用问题具有现实意义与规律.

3 重视数学思想方法与技巧策略的提炼

概率统计模块知识也离不开数学基本思想方法与技巧策略,成为聚焦数学核心素养,以及提升数学关键能力的一个重要场景.特别是以实际应用题为场景的概率统计问题,更是突出数学核心素养与关键能力的一个基本场所.

基于此,在复习备考过程中,要全面把握数学基本思想方法的引领,指向数学基本技巧策略应用.要将数学的思想方法与技巧策略等贯穿在复习备考与数学解题过程中去,使得复习备考过程更加全面体现数学经验积累和数学思想升华.

例3为调查中某校学生每天学习的时间,采用样本比例分配的分层随机抽样,现抽取高一学生400人,每天学习时间均值为8小时,方差为0.5,抽取高二学生600人,每天学习时间均值为9小时,方差为0.8,抽取高三学生1 000人,每天学习时间均值为10小时,方差为1,则估计该校学生每天学习时间的方差为( ).

A.1.25 B.1.35 C.1.45 D.1.55

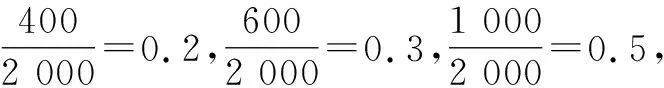
结合分层随机抽样的样本方差公式,可得到s2=0.2×[0.5+(8-9.3)2]+0.3×[0.8+(9-9.3)2]+0.5×[1+(10-9.3)2]=1.45.

故选：C.

点评：在解决一些复杂的分层随机抽样问题时,首先要准确确定分层随机抽样的层数,以及确定与之相关的基本概念(样本总数、各层的样本数或频率等),进而熟练利用分层随机抽样的样本平均值、样本方差公式加以推理与运算,并结合实际问题的应用场景与现实实际来合理判断与决策等.

4 重视数学知识内涵与解题过程的规范

概率统计模块知识的应用,是阅读材料与数学知识之间的联系与转化,也是对材料信息的再认识与再加工.在实际解决问题时,需要将对应的应用情境问题加以合理抽象,巧妙建模,利用数据分析与信息加工,并结合数学运算与逻辑推理等来分析与解决问题.

基于此,在复习备考过程中,需要重视数学知识内涵的提炼,重视数学解题过程的规范、解题格式的训练,特别对于数学符号的使用要规范准确,语言表达精炼准确,逻辑推理严谨,数学运算正确.

5 重视未涉及知识的教学复习

近两三年来高考没有考到的内容：正态分布、一元线性回归模型等相关问题.随着“教学评一体化”及人才选择培养体系的变革,这一部分内容将会成为来年高考的考点,需要教师与学生务必做好这些知识点的教学与复习,使得复习更加系统,更加全面,更加到位.

近年高考中,概率统计模块知识的考查更加吻合《普通高中数学课程标准(2022修订)》,突出该模块中的基本概念、主干知识以及基本数学方法与技巧策略等方面的考查等,吻合教材的内容比例,全面考查知识的应用等,特别在通性通法的基础上,进行适度的综合与创新.