课例：函数的奇偶性

⦿ 广东省东莞市第一中学 陈 鑫

⦿ 广东省东莞市第六高级中学 汤高敏

1 教学内容分析

“函数的奇偶性”是人教A版数学必修第一册第三章第二节的内容.一方面,函数的奇偶性是继函数的单调性后的又一重要性质,它延续了研究函数单调性的方法;另一方面,它也为后续研究函数的周期性以及幂函数、三角函数等奠定基础.

1.1 教学目标

(1)经历函数奇偶性的探究过程,进一步体会研究函数性质的一般方法;

(2)通过对具体函数奇偶性的探究,会用符号语言刻画函数图象关于y轴或原点对称,了解函数奇偶性的概念和几何意义,体会奇偶函数命名的由来;

(3)会利用函数奇偶性的定义和函数图象特征判断具体函数的奇偶性;

(4)在函数奇偶性概念的形成过程中感受数形结合、从特殊到一般的数学思想.

1.2 教学重点与难点

教学重点：函数奇偶性的概念和几何意义.

教学难点：从具体函数的图象特征到数量刻画,再进一步抽象出符号语言的过程.

2 教学过程

2.1 情境引入

师：我们是如何研究函数的单调性和最值的?

生1：具体函数—图象特征—数量刻画—符号语言—抽象定义.

师：下面我们将继续采用这种研究方法研究函数的其他性质.

设计意图：复习研究函数性质的一般思路、方法,为接下来研究函数的奇偶性做准备.

2.2 新知探究

师：请同学们画出函数f(x)=x2和g(x)=2-|x|的图象,并观察这两个函数图象有什么共同特征?

生2：如图1,这两个函数的图象都关于y轴对称.

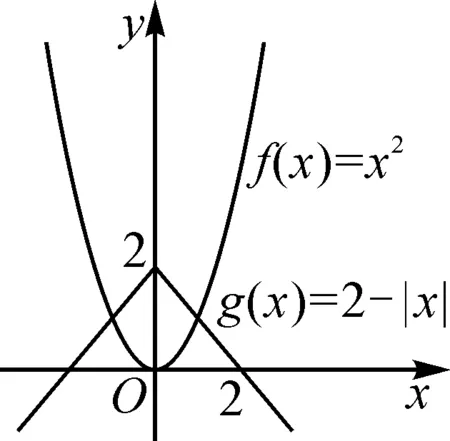
图1

设计意图：引导学生发现偶函数的图象特征.

师：我们以f(x)=x2为例,探究如何从数的角度刻画其图象关于y轴对称.

师：由于图象本质上是由点所构成的集合,我们不妨取一些特殊点来观察.

师：观察表1数据,同学们能发现什么?

表1

生3：f(-3)=9=f(3);f(-2)=4=f(2);f(-1)=1=f(1).当自变量取一对相反数时,对应的函数值相等.

师：这个规律是否具有一般性?我们借助信息技术来看一看(利用GGB演示：在f(x)=x2图象上任取两点,当这两点横坐标互为相反数时,纵坐标相同).

师：也就是说,“图象关于y轴对称”等价于“自变量互为相反数时,函数值相等”.

设计意图：由“形”到“数”,得到函数图象关于y轴对称的数量刻画.

师：那现在我们就得到了函数f(x)=x2的图象关于y轴对称的数量刻画.进一步地,如何用符号语言来描述呢?

生4：∀x∈R,都有f(-x)=(-x)2=x2=f(x).

设计意图：让学生自然地得到“函数f(x)=x2图象关于y轴对称”的符号语言表征,并在过程中体会“∀”符号的由来,发展学生逻辑推理核心素养.

师：请同学们仿照上述表达方式,用符号语言描述g(x)=2-|x|的图象关于y轴对称.

生5：∀x∈R,都有g(-x)=2-|-x|=2-|x|=g(x).

设计意图：借助实例让学生进一步熟悉函数图象关于y轴对称的符号语言表征,并为后续抽象出偶函数的符号语言表征做准备.

师：如何用符号语言描述函数y=f(x),x∈I的图象关于y轴对称?

生6：∀x∈I,都有f(-x)=f(x).

设计意图：从具体函数到一般函数,体现了从特殊到一般的思想,发展学生的抽象概括能力及数学抽象核心素养.

师：如果一个函数的图象关于y轴对称,那它的定义域有什么特点?

生7：定义域关于原点对称.

师：鉴于定义域对函数奇偶性判断的重要性,我们将上述所得的符号语言作进一步补充,即∀x∈I,-x∈I,且f(x)=f(-x).一般地,我们把满足这一条件的函数叫做偶函数.

设计意图：让学生发现定义域对函数奇偶性判断的重要性,并在定义中将定义域关于原点对称这一条件显性化.

师：接下来请通过小组合作,探究以下问题.

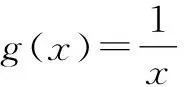
(2)如何用符号语言准确描述这一共同特征?

(3)如何用符号语言准确描述函数y=f(x),x∈I的图象关于坐标原点对称?

生8：(1)……;(2)……;(3)∀x∈I,-x∈I,且f(-x)=-f(x).

师：类似地,我们把满足这样条件的函数叫做奇函数.

设计意图：放手让学生通过类比的方式研究奇函数,不仅能促进数学知识、方法的有效迁移,还能加深学生对奇偶性概念的理解.

师：在前面的学习中,我们定义了两类新的函数,分别是偶函数和奇函数.那同学们知道为什么要这样命名吗?

师：我们不妨来分别观察两组函数y=x2,y=x4,y=x6与y=x,y=x3,y=x5的图象,说说它们分别具有怎样的对称性?(用几何画板呈现图象.)

生9：y=x,y=x3,y=x5的图象关于坐标原点对称,y=x2,y=x4,y=x6的图象关于y轴对称.

师：请同学们再观察一下,上述函数中,图象关于y轴对称的函数的自变量的次数有什么特点?关于坐标原点对称的呢?

生10：上述函数中,图象关于y轴对称的函数的自变量的次数都为偶数,图象关于原点对称的函数的自变量的次数都为奇数.

师：同学们得到了一个伟大的发现!实际上,著名数学家欧拉正是由此首次提出了奇、偶函数的概念.后来随着数学的发展,奇、偶函数又进一步得到了推广,形成了如今的奇、偶函数概念.

设计意图：借助部分正整数次幂的幂函数图象,让学生发现其共同特征——对称性,并通过追问发现规律,从而引出奇、偶函数的概念,让学生经历奇函数、偶函数概念的产生过程,了解命名的由来,获得良好的数学体验.此外,通过穿插数学史,学生能体会其中所蕴含的数学文化,提高数学学习的兴趣.

2.3 数学运用

练习1判断下列函数的奇偶性：

设计意图：再一次体会定义域对函数奇偶性判断的重要性,掌握用定义判断函数奇偶性的一般步骤.

练习2(1)判断函数f(x)=x3+x的奇偶性.

(2)图2是函数f(x)=x3+x图象的一部分,你能根据它的奇偶性画出它在y轴左边的图象吗?

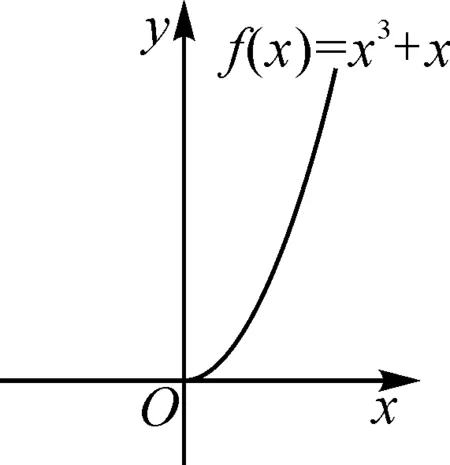
图2

(3)一般地,若y=f(x)为奇(偶)函数,如何简化对它的研究?

设计意图：进一步让学生巩固利用定义判断函数奇偶性的方法,学会根据奇函数、偶函数图象的对称性解决问题,体会奇偶性的作用——简化对函数的研究.

练习3已知f(x)是R上的奇函数,且当x∈(0,+∞)时,f(x)=x(1+x),求f(x)的解析式.

设计意图：让学生学会利用奇偶性求函数的解析式.

2.4 回顾小结

(1)我们是如何开展对函数奇偶性的研究的?

(2)完成表2：

表2

(3)如何用定义判断函数的奇偶性?

设计意图：通过(1),进一步深化对研究函数性质的一般方法的认识,提升研究性思维.通过(2),加深对奇、偶函数概念和几何意义的理解.通过(3),进一步掌握用定义判断函数奇偶性的一般方法、步骤.