多样化策略孕育优化思想

张国全 龚莉

《义务教育数学课程标准（2022年版）》提出“会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界”的素养目标。教学人教版数学五年级下册第八单元《数学广角——找次品》时，教师如何设计能够引导学生运用多样化策略解决问题的探究活动，培养学生的优化思想，落实“三会”素养目标呢？

一、聚焦简单问题，初步感知找次品的思路

“找次品”学习活动具有很强的探究性，教师应从简单问题入手，让学生在自主探究中初步感知找次品的含义与基本思路。

课始，笔者用多媒体出示例题：“有3瓶钙片，其中1瓶少了3片。像这样不符合标准要求的物品称为‘次品。我们就把这瓶轻的看作次品。你能设法把它找出来吗？”学生提出用手掂一掂的方法，于是笔者让几名学生上台实践。尝试之后，学生都反映质量差距太小，感觉不出哪一瓶少了3片。笔者引导：“你们玩过跷跷板吗，它有什么特点？”学生回答：“玩跷跷板时，重的一端下降，轻的一端上升。”“什么工具能像跷跷板那样，帮助我们直接找出次品呢？”笔者进一步引导。“用天平称！”学生回答。笔者没有提供真正的天平，而是让学生同桌合作，用橡皮和直尺模拟天平，用3张分别标有数字①②③的卡片代表3瓶钙片，在“天平”上模拟称一称，并说一说各自的想法。同桌交流后，笔者让一名学生在展台上边演示边描述怎样找次品，需要称几次。学生操作并讲解：“‘天平两端分别放①和②，如果平衡，次品就是外边的③；如果不平衡，次品就是上升端的那一瓶。称1次就能找出次品。”笔者追问：“外边的③为什么不用称？”学生补充：“只要同时称①和②，③的情况就可以推理出来。”笔者接着说：“所以，天平还有‘第三个称盘，它其实在我们心里。”通过思考与操作，学生明白了次品出现的地方可能在天平的左边，可能在天平的右边，也可能在天平的外边。

“找次品”中的天平应该是一架抽象的天平。一旦用实物天平进行实验，将剥夺学生发展逻辑推理能力的机会。在解决问题的过程中，教师要逐步引导学生在头脑中建立天平的表象，反复进行“如果平衡，那么……如果不平衡，那么……”的思维过程，进而感知找次品的基本思路。

二、抓住解题关键，体验找次品分组的多样性

教师要紧扣教材，引导学生对比探究从8个、9个物品中找次品的问题，在猜测、推理、归纳的过程中，感受解题策略的多样化，发现解题规律。

课堂上，笔者出示“8个零件里有1个是次品（次品重一些）。假如用天平称，至少称几次能保证找出次品？”的问题，先引导学生理解“至少”和“保证”的含义，使他们明确“保证”要求每一条可能的途径都被考虑到，不能停留在“运气好”的情况；“至少”要求在保证找出次品的各种方案中找到称量次数最少的方案。然后，笔者让学生用自己喜欢的方式将分法、称的次数及推理过程记录下来。汇报时，一名学生说：“先把8个分成4个和4个，天平两端各放4个，如果天平不平衡，次品就在下降端的4个中；然后把4个分成2个和2个再称，如果天平不平衡，次品就在下降端的2个中；最后把2个分成1个和1个再称，次品就是下降端的那一个。需要称3次。”对这种称法，笔者没有马上回应，而是给出从9个零件中找1个次品（次品重一些）的问题，引导学生通过对比与质疑，强化对“至少”和“保证”含义的理解。

探索从9个零件中找1个次品（次品重一些）的问题时，笔者让学生画图记录找的过程，并小组讨论次数最少的称法。有的小组将9分成（4，4，1），发现需要称3次。一名学生质疑：“我也是这样分的，天平两边各放4个称量时，称一次就找出次品了，为什么还要继续称呢？”另一名学生解释：“这样分，称一次就找出次品是运气最好的情况，但不是能保證找出次品的情况，所以我们应该在最不利的情况下推理。”从最不利的情况来看，将9分成（4，4，1）是称的次数最少的分组方法吗？笔者请一名学生展示将9分成（3，3，3）的称法：“如果天平平衡，次品就在天平外的3个中；如果天平不平衡，次品就在下降端的3个中。接下来从3个里面找，将3分成（1，1，1），如果天平平衡，次品就是天平外的那一个；如果天平不平衡，次品就是下降端的那一个。这样分只需要称两次。”笔者组织学生小组讨论把9分成（4，4，1）的称法和把9分成（3，3，3）的称法的不同之处。学生发现：一个是平均分，另一个不是平均分；平均分后，不但能保证找出次品，而且称的次数最少。

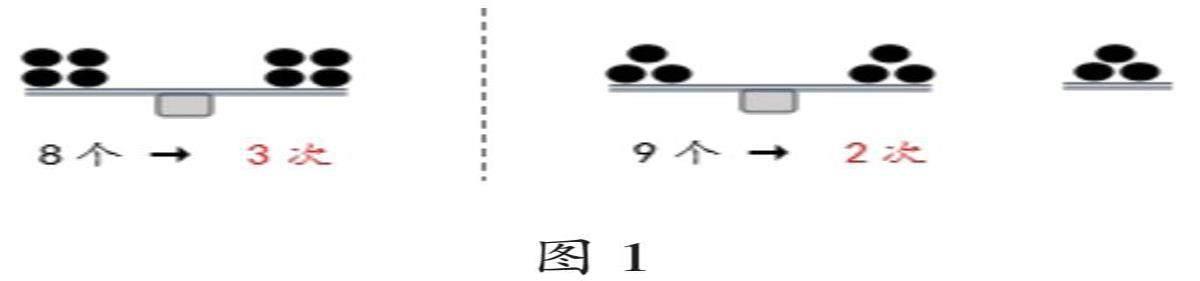
接下来，笔者投屏展示把8分成4，4和把9分成3，3，3找次品的直观图（如图1），让学生在对比中产生新的思考，为“一分为三”优化策略的提炼做铺垫。

学生观察图1后质疑：“为什么零件总数多了，找次品的次数反而少了呢？”笔者鼓励学生聚焦从8个零件中找次品的零件分法的优化，展开小组合作探究，并将零件分法和称的次数等实验数据记录在表格中，找出哪种分法称的次数最少，以便进一步感悟“一分为三”策略的优越性。

三、发现规律，渗透优化思想

“找次品”探究活动的设计需要遵循由简单到复杂、由特殊到一般的原则，让学生在比较、猜测、验证的活动中逐步感悟、总结和提炼找次品的基本策略，发现规律并应用规律解决更复杂的找次品问题，进一步归纳、概括出解决这类问题的最优方法。

小组合作探究并完成表格后进行汇报，学生发现与“（2，2，2，2）；（4，4）；（2，2，4）；（1，1，1，1，1，1，1，1）”等分组情况相比，把8分成3，3，2时称的次数最少，只需要称两次。笔者质疑：“都是从8个零件中找次品，怎么称的次数不一样？”学生一时无法清晰地表达自己的想法。笔者启发：“如图2，左边这种分法称为‘一分为二，次品可能在哪里？右边这种分法称为‘一分为三，次品可能在哪里？”

表面上看，“一分为三”比“一分为二”多了一个盘子，能帮助我们多推理出一种情况。实际上，“一分为二”也有第三个盘子（天平外部），只不过我们没有向里面放入零件，盘子是空的，就起不到帮助我们推理的作用了。这导致我们称的次数变多了。也就是说，“一分为三”可以将次品确定在更小的范围内。学生在笔者提示下结合图示和操作过程理解了“一分为三”的优势后，笔者让学生思考把8分成（3，3，2）时，每份的数量有什么特点。学生发现每份的数量都比较接近，其中有两份数量相等。笔者引导学生对比分析把8分成（3，3，2）和把9分成（3，3，3）的情形，进而总结出分组的优化策略：分三组，尽可能平均分；如果不能平均分，让每组的数量尽可能接近，并且三份中有两份数量相等。

在此基础上，笔者依次引导学生解决从10个、11个、28个、81个物品中找次品的问题，以巩固、应用分组的优化策略，进一步体会“找次品”问题所蕴含的优化思想的本质——每次称重都要将次品限定在最少的数量中。

（作者单位：张国全，枣阳市第四实验小学教联体；龚莉，枣阳市第四实验小学教联体靳庄校区）

责任编辑  刘佳