在操作想象中理解 在对比反思中提升

屈婷

“找次品”是在学生学习了“沏茶问题”“烙饼问题”“打电话问题”的基础上教学的。本课旨在通过一系列“找次品”活动，让学生在寻找最优方案的过程中逐步体会优化的本质。

一、在操作和想象中探索基本思路

“找次品”活动的实质是用虚拟的天平作为工具，帮助学生想象每称一次后天平“平衡”与“不平衡”的画面，再通过逻辑推理，逐步缩小次品所在的范围，直至确定次品。

新课伊始，笔者出示问题情境：有3瓶钙片，其中1瓶少了3片，我们将它看作次品，你能设法把它找出来吗？学生思考后回答：因为次品只少了3片，与其他两瓶质量相差不多，用手不容易掂出来，倒出来数既耗时又不卫生，用天平称一称比较简单。笔者出示一架纸质天平，并提问：你打算怎样称？有的学生认为可以将天平的一端放钙片，另一端放砝码，称出每瓶钙片的具体质量，再做比较；还有的学生认为无须称出3瓶钙片的具体质量，将天平的两端分别放一瓶钙片，只要天平不平衡，轻的那边就一定是次品。通过交流，学生都认为第二种称法更简单。笔者先让学生借助纸天平和钙片卡片演示找次品的过程，并跟同桌说一说怎样称的。接着，笔者展示如下两种学生的不同称法，并引导学生思考这两种称法是否都能找到次品。

学生提出，方法①中天平的两个托盘里放的钙片瓶数不一样，不管哪一瓶是次品，都是左边重右边轻，找不到次品；方法②中天平的两个托盘里各放了一瓶钙片，天平的右边轻，所以2号是次品。笔者追问：按照方法②来称，一定会出现这种结果吗？还可能出现什么结果？这样称一定能找到次品吗？一名学生回答：天平还可能平衡，这样称一次就找不到次品，还需要将天平一端的一瓶换成第3瓶继续称。另一名学生认为不需要换，如果天平平衡，说明1号和2号都可以排除，不是次品，只有1瓶次品，它一定是3号。

学生对从3个待测物品中找一个较轻次品的基本推理思路有了清晰的认识之后，笔者让学生用画图的方式记录用天平找次品的推理过程，并思考需要称的次数，逐步找到次品。

二、在对比和交流中感知分组特点

教学中，教师可以设计“从8个物品中找次品”的活动，更好地促进学生对“非3的倍数”的物品最优分法的感悟，引导学生发现最优方案的分组特点。

笔者先出示问题：“8个零件中有1个是次品（次品重一些）。假如用天平称，至少称几次能保证找出次品？”学生读题后，画图表示用天平找次品的过程。随后，笔者呈现如下两种学生的方法，并提问：这两名学生第一次是怎样称的？可能出现哪些结果？根据称的结果，我们可以推理得到哪些结论？

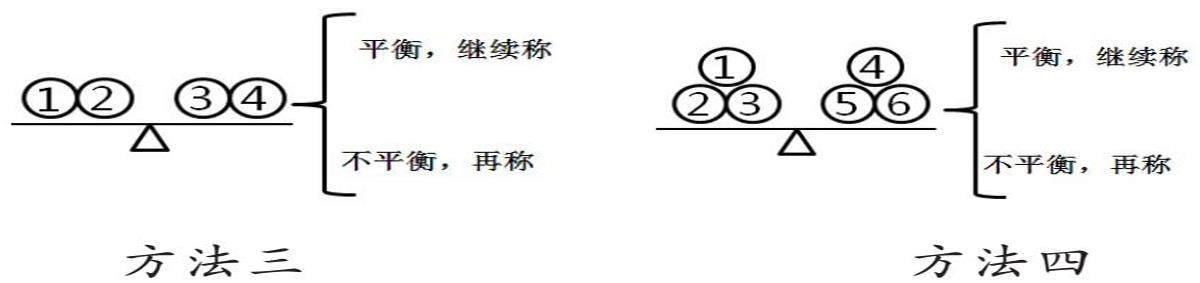
学生认为方法一在运气好的情况下一次就能找出次品，如果运气不好，天平平衡，只能排除两个零件不是次品。对于方法二，学生出现了争议。一部分学生认为这样称没有考虑全面，还需要考虑天平平衡的情况。另一部分学生认为这样称只会出现一种情况，如果天平平衡就不存在次品，如果天平不平衡，可以排除不是次品的4个零件。然后，笔者呈现如下方法三和方法四，并提出一系列问题：这两种称法考虑得全面吗？出现什么情况对我们最有利？出现不利情况时，哪种放零件的方法更好？与方法一、方法二相比，哪种称法第一次称后排除的数量更多？为什么？

通过对比和交流，学生发现，方法一和方法三中，天平上放的零件个数太少，遇到天平平衡这种不利情况，虽然可以排除天平两端的不是次品，但剩下的零件范围大，不利于找次品；方法二把零件全部放在天平上，只能排除一个位置的零件不是次品，也不利于找次品；方法四剩下的零件数量和天平两端各自放的零件数量差不多，不管天平平衡还是不平衡，能排除掉的零件数量都差不多，有利于找次品。笔者继续设疑：按照方法四的称法，如果平衡，第二次需要從几个物品中找次品？如果不平衡，第二次需要在几个物品中找次品？学生探究发现方法四是最优称法后，笔者顺势将这种分法的记录方式简化成“8（3，3，2）”。

通过不同方法的比较，学生体会到第一次称时，要尽量从最不利的情况思考，不管天平平衡还是不平衡，都可以排除一些零件；只有天平左盘、天平右盘、天平外都有零件且相差1个时，排除的范围最大，次品所在的范围最小。

三、在反思和归纳中探寻最优策略

最优策略应该保持一致性，也就是每次操作时都应遵循相同的原则。当零件总数较特殊时，容易产生两种方案所用次数相等的巧合。教学中，教师要精心设计探究材料，让学生在对比、反思中归纳出“找次品”的最优策略。

笔者提问：如果9个零件中有1个次品（次品重一些），至少称几次能保证找出次品？你是怎样称的？学生用简化的记录方式表达自己的想法，提出（3，3，3）和（4，4，1）两种分法。笔者提问：这两种分法第一次称时可能出现几种情况？在不利情况下可以排除几个零件？第二次称要从几个物品中找次品？通过讨论和交流，学生发现：前者天平两端和天平外的零件数相同，无论天平平衡还是不平衡，都可以排除6个零件，第二次从3个零件中找即可，后者如果遇到天平不平衡的情况，只能排除5个零件，第二次称要从4个中找次品，所以，平均分成3份称的次数最少。

接下来，笔者出示问题：10个零件中有1个次品（次品重一些），至少称几次能保证找出次品？通过计算，学生发现：10个零件如果分成（4，4，2），天平平衡时可以排除8个零件，天平不平衡时可以排除6个零件，第二次称需要从2个或4个零件中找；如果分成（3，3，4），天平平衡时可以排除6个零件，天平不平衡时可以排除7个零件，第二次称只需要从4个或3个零件中找。要保证找到次品，两种方法都至少需要称3次。

由于第二次称时都需要考虑从4个零件中找次品，部分学生误认为最多的一份与最少的一份相差2也是最优方法。对此，笔者提出“26个零件，如何找出一个稍重的次品”的问题，请学生至少用两种最优方法进行推理。学生发现：26个零件如果分成（8，8，10），天平平衡时可以排除16个，天平不平衡时可以排除18个，第二次称需要从10个或8个中找；如果分成（9，9，8），天平平衡时可以排除18个，天平不平衡时可以排除17个，第二次称只需要从8个或9个中找。从10个零件中找一个较重的次品至少需要称3次，按照第一种分法，从26个零件中找次品至少需要称4次。从8个或9个零件中找次品都只需要称两次，按照第二种分法，从26个零件中找次品只需要称3次。笔者追问：前面你们说三份中最多和最少的相差1个或2个所用次数都是最少的，这里为什么行不通了？通过小组讨论，学生发现：零件总数是10个时，最多的一份都是4，两种分法没有明显差异，而零件总数是26个时，两种分法的最多的一份出现了不同情况，只有把零件总数尽量平均分，才能保证下一次称时次品所在的范围最小。

经历上述活动，学生能够借助语言和画图清晰而有条理地表达用天平找次品的推理过程，感悟到“找次品”活动的优化本质。

（作者单位：宜城市窑湾小学）

责任编辑  张敏