数学思想在教材和教学中的显性化

李景财 刘稳定

数学思想蕴含在数学知识形成、发展和应用的过程中，是对数学知识与方法的本质认识和更高层次的抽象与概括，是从具体数学认识过程中提炼出的观点。它与数学核心素养一脉相承，可作为发展学生数学核心素养的重要载体。数学思想导向的教学是比数学知识技能教学更上位的教学，有利于达成数学核心素养目标和学科育人目标。然而，数学思想往往是隐性的，实施数学思想导向的课堂教学首先要将数学思想显性化。

一、教材研究中数学思想的显性化

义务教育数学课程标准虽然指明数学思想是“四基”之一，但没有系统介绍数学思想，教材也没有把数学思想凸显出来。为帮助教师整体把握初中数学课程内容所蕴含的数学思想，在教学中准确地提取与渗透数学思想，笔者对照《义务教育数学课程标准（2022年版）》，将初中数学教材中蕴含的数学思想做了显性化处理。

1.建构数学思想结构图

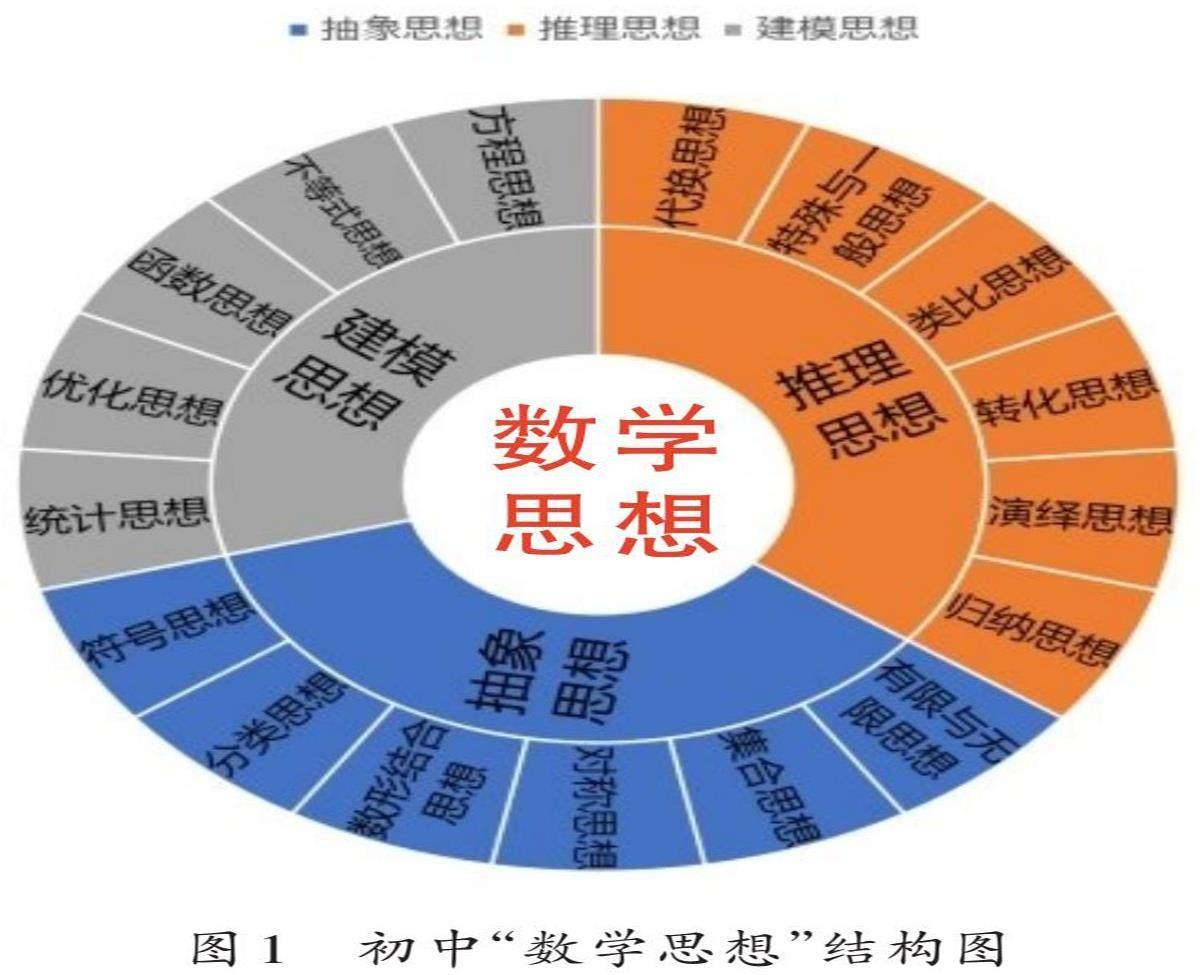
史宁中教授指出，数学基本思想主要有抽象、推理和建模，由此演变、派生出一系列数学思想，如转化与化归思想、类比思想、归纳思想、分类思想、数形结合思想、方程与函数思想、特殊与一般思想等。基于此，笔者在查阅大量资料的基础上，梳理了人教版初中数学教材中常见的数学思想，构建了如图1所示的初中数学思想结构图。

该结构图将人教版初中数学教材内容涉及的主要数学思想按照抽象、推理、建模三类进行归纳，有利于教师从整体上明晰初中阶段的数学思想内容框架。

2.研制数学思想细目表

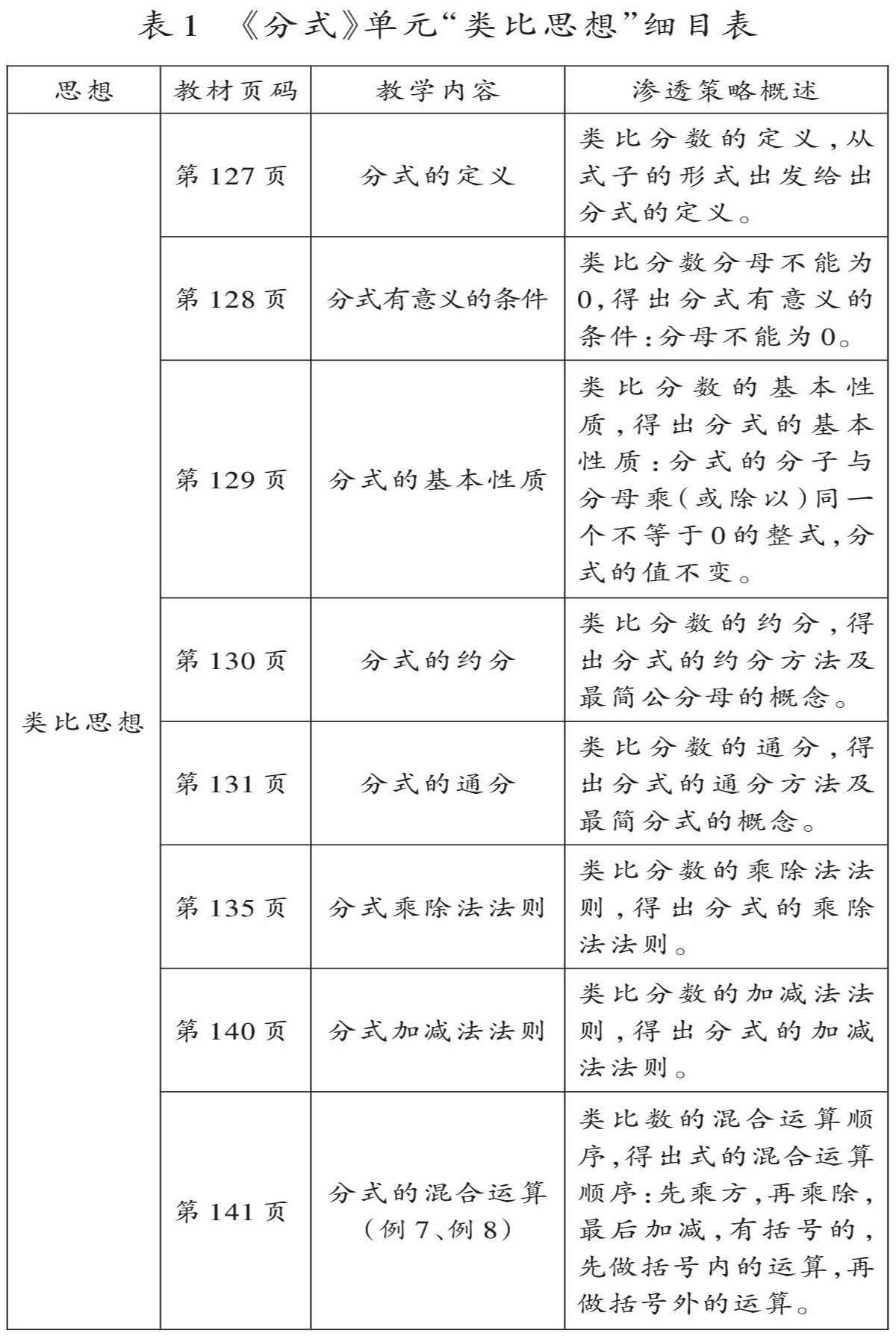
为方便教师准确把握教材内容所蕴含的数学思想，明确课堂教学中数学思想的渗透点，笔者结合初中数学思想结构图，依托人教版七至九年级数学教材，从教材内容主要蕴含了哪些数学思想、怎样体现数学思想两个维度进行研究，编制出各单元的数学思想细目表。表1是八年级上册第15章《分式》单元“类比思想”细目表。

该表梳理了《分式》章节中体现类比思想的具体内容及页码，并基于已有研究成果和经验，概述了在相关内容教学中渗透类比思想的具体策略，有助于教师正确把握数学思想导向的课堂教学定位，设计合适的教学目标和教学活动。

二、教学研究中数学思想的显性化

1.拟定聚焦数学思想的学习目标

數学思想导向的课堂教学应该像具体的数学表层知识教学一样，拟定明确的、可控的、符合学生认知规律的学习目标。例如，《整式的加减》单元复习课中，一名教师结合课程标准相关学段要求，通过分析《整式的加减》单元教材内容，构建了如下聚焦数学思想的单元目标：①通过类比数的运算，从运算的视角理解单项式与多项式的相关概念，构建单元知识框架，发展抽象能力、模型观念；②类比数的加减运算经验，掌握整式的加减运算法则，学会选择适当的方法进行整式的加减运算，发展运算能力、推理能力；③在运用整式加减运算法则解决问题的过程中积累运算经验，提升发现问题、解决问题的能力，发展推理能力和应用意识。

2.研制运用数学思想解决问题的教学流程图

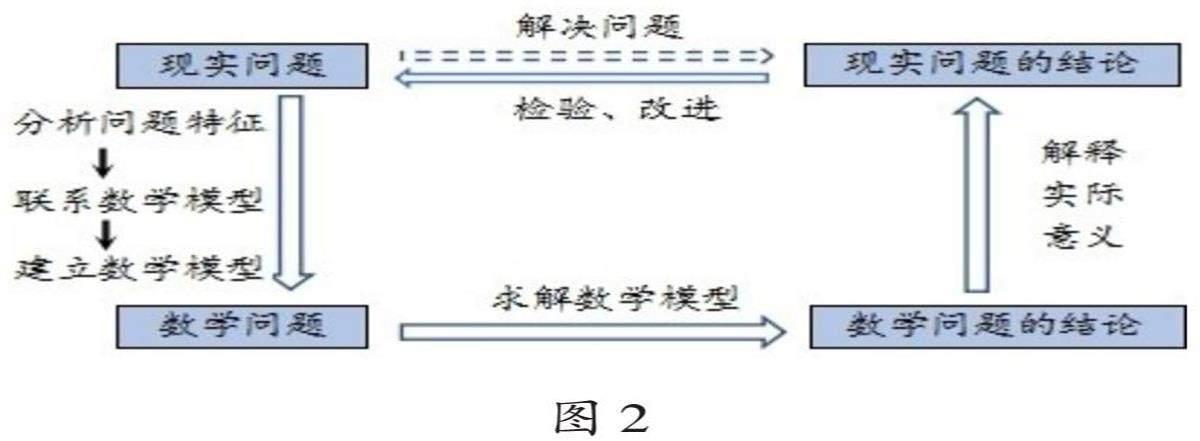
笔者通过实践探索，构建了数学思想导向的课堂教学实施策略和操作流程，并用思维导图把运用数学思想解决问题的教学过程表达出来，从而使基于数学思想的解决问题的教学过程显性化。图2是运用建模思想解决问题的教学流程图。其中，关键步骤呈现在相应的方框里，数学行为呈现在白色箭头旁。

从图2可以看出，运用建模思想解决问题的教学流程要从现实问题开始，首先引导学生分析问题特征，联系数学模型，建立数学模型，进而抽象出数学问题；接着引导学生求解数学模型，得到数学问题的结论；然后引导学生通过解释数学问题及其结论的实际意义，归纳出现实问题的结论；最后引导学生依托现实问题的背景和实际意义，检验与改进现实问题的结论，从而解决现实问题。

三、数学活动中数学思想的显性化

数学思想与数学活动紧密关联。如果没有数学思想方法的指导，学生即使在数学活动中获得了知识、解决了问题，其学习所得也很可能是数学事实的堆砌，解决问题教学的指向被弱化为简单技能的积累，难以使学生形成数学思想层面的认知，积累有效的、可迁移的经验。为此，教师不仅要在知识的形成和应用等数学活动中引导学生总结、提炼数学思想方法，还要在应用数学思想方法解决变式问题的过程中深化学生对数学思想方法的理解，更要在课堂小结中着力凸显数学思想方法，使学生形成有条理的认知。

1.在解题反思中概括数学思想

数学思想方法的建立需要经历一般化、程序化和模式化的抽象过程。缺少了这样的抽象过程，学生在具体问题解决中形成的思想方法就很难一般化，也很难进行有效的迁移。因此，在数学思想方法教学中，教师应该引导学生对数学活动经验进行概括，尤其是在解决问题之后，通过反思、总结来概括。例如，在学生经历了根据一些实际问题建立方程，并通过解方程来解决实际问题的数学活动后，教师可以引导学生把具体做法一般化、程序化，并把这个过程抽象概括为某种数学思想方法的运用。这个从具体到抽象的过程可以帮助学生形成可迁移的数学思想方法。

2.在迁移应用中深化数学思想

数学思想方法的巩固、深化需要充分的案例积累。在应用某种数学思想方法解决不同形式、不同领域问题的过程中，学生可以熟练掌握这种思想方法，体会这种思想方法的一般化、程序化和模式化。这是一个从抽象到具体的过程，是促进学生把数学思想方法应用于新情境、产生远迁移的关键环节。例如，在一元一次方程的学习中，学生已经经历了方程思想的体悟过程，但要使方程思想内化于学生的大脑中，让学生在各种情境下都能自如运用方程思想解决问题，则需要在一元二次方程、二元一次方程组、分式方程等内容的学习中，进一步强化学生用方程思想解决问题的意识和能力，使其在各种方程的建模实践中巩固、深化方程思想。具体来说，学生能有意识地运用方程思想建立问题中的数量关系，并通过解方程间接地获得问题的解，使运用方程思想解决问题的过程内化于心，就达到了方程思想的程序化和模式化水平。

3.在课堂小结中凸显数学思想

课堂小结要体现知识的建构过程，凸显思想方法的提炼过程。以《等腰三角形的性质》课堂小结为例。教师从知识技能和思想方法两个方面引导学生建构本节课的知识结构图。首先，教师提出“本节课主要学习了哪些内容”“本节课学习了哪些添加辅助线构造全等三角形的方法”两个问题，引导学生回顾“等腰三角形是轴对称图形”“等边对等角”“三线合一”等知识点，以及“作等腰三角形顶角的平分线、底边上的中线、底边上的高”等作辅助线的技能。然后，教师通过追问“已知等腰三角形的一角，求其他两角时要注意什么”“等腰三角形中，已知内角的关系，求角度要运用什么思想”，引导学生提炼“要注意按顶角或底角进行分类”“要运用方程思想”等思想方法。最后，教师总结本节课师生共同经历的探究等腰三角形性质的过程：“本节课，我们经历了操作、观察、猜测、证明等过程，即从合情推理到逻辑推理的过程。”上述课堂小结过程中，在学生作答的基础上，教师用大括号把知识技能、思想方法分别括起来，以加深学生的印象。

这样小结，不仅帮助学生建构了本节课的知识结构，提炼了本节课的学习过程，还帮助学生积累了学习几何知识的路径与经验，有效促进了学生数学核心素养的发展。

（作者单位：李景财，武汉市光谷第八初级中学；刘稳定，武汉东湖新技术开发区教育发展研究院）

李景财，湖北省特级教师，湖北省数学学会数学教育专业委员会理事，武汉东湖新技术开发区首届“十大名师”。从2018年开始，李景财引领工作室成员依托“富有数学思想的初中课堂教学策略研究”课题展开教学研究。历经4年，该课题于2022年结题并获评优秀成果。2023年，工作室以此课题为基础建构的“显化·渗透·条理·升华：初中数学思想五年学科实践”项目在“湖北好教研”评选活动中获得一等奖。本组文章聚焦相关研究成果，阐释数学思想导向的课堂教学的设计与实施经验。