基于“教-学-评”一体化的作业目标设定

张春莉 曹辰

张春莉

北京师范大学教育学部课程与教学研究院院长，教授、博士生导师；中国教育学会小学数学教学专业委员会副秘书长，中国教育发展战略学会教育教学创新专业委员会副理事长，中国少数民族教育学会数学教育专业委员会副理事长；主持的课题有全国教育科学“十一五”规划教育部重点课题“新课程小学数学、语文学科能力评价研究”、全国教育科学“十二五”规划教育部重点课题“读懂中小学生数学学习过程的方法研究”，以及国家自然科学基金面上项目“复杂情境下学生数学创造性思维的认知及脑机制研究”等；著有《小学生数学能力评价研究》《小学数学互动式教学》《学习者视角下的学习历程分析》等专著，发表学术论文100余篇。

近年来，随着教育改革的不断推进，“教-学-评”一体化成为教育教学的一个重要方向。《义务教育数学课程标准（2022年版）》（以下简称“2022年版课程标准”）基于此理念，提出发挥评价的育人导向作用，坚持以评促学、以评促教，使得教学活动中学生学习的评价、学生的学、教师的教都指向教学目标，并且协调统一。在“教-学-评”一体化的教学模式中，作业设计扮演着关键角色。作业目标是作业设计的重要导向，通过合理设计目标，教师能够有针对性地进行教学，促进学生学业进步和能力发展。基于此，本文将探讨基于“教-学-评”一体化的作业目标设定的关键要素和作业目标达成度的评估方法，为教育教学实践提供一些建设性的思考和借鉴。

一、明确认知行为：构建任务规划表，支持单元视角下的“教-学-评”一体化

根据教育心理学家杰罗姆·布鲁纳（Jerome Bruner）的观点，教材是教学的核心，通过深入理解教材，学生能够建立知识的结构和意义，从而更好地应用所学知识。教材作为教学的核心素材在作业设计中具有重要作用。从认知活动的角度对教材内容进行解读，有助于教师深入理解教材内涵，并将其转化为具体的认知任务。这种解读方式能够提供更明确的指导，帮助教师规划每节课的认知发展目标，并设计相应的作业，以促进学生深度理解，提高知识应用能力。基于此，教师从深挖教材逻辑、了解教材内涵的角度出发，结合认知活动的解读，可以将作业目标设计与教材以及素养要求紧密关联起来，确保作业有效地支持学生的学习进程，提升教学效果。教师应将2022年版课程标准“学业质量”板块提出的学习目标转化为具体的认知行为要求，通过对教材具体活动的解读，划分每节课的教学内容和认知任务，确保作业目标与教材内涵和认知活动相契合，从而形成单元合力，推动学生形成学习成果，发展核心素养。从认知活动的角度解读单元教材是作业目标设计的第一步。

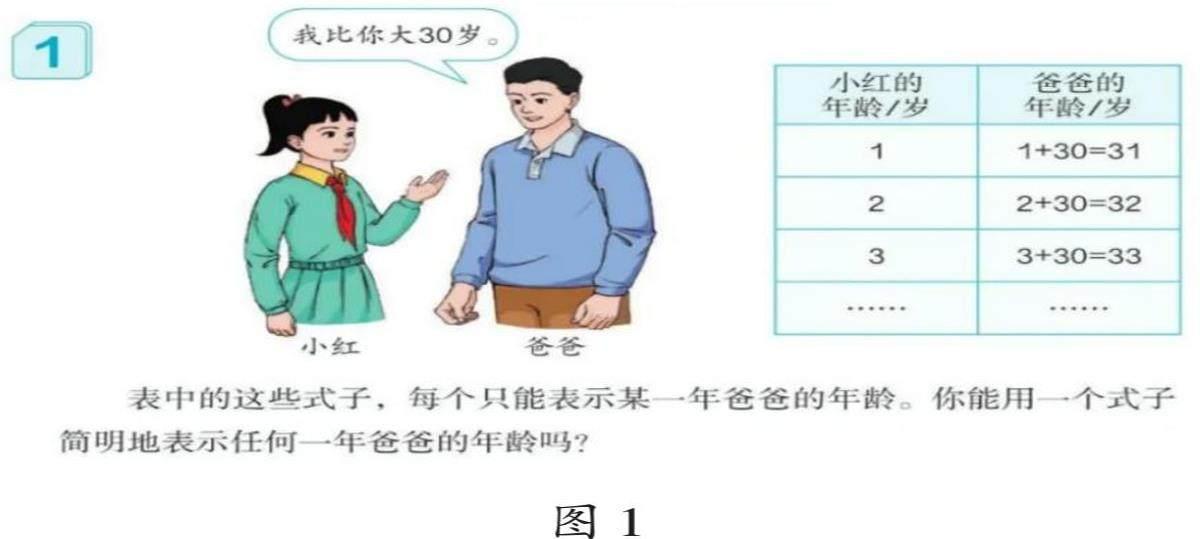
以人教版数学五年级上册《简易方程》单元例1（如图1）为例。这个活动旨在引导学生探究“如何用一个式子简明地表示任何一年爸爸的年龄”。从认知角度看，该教学活动涉及举例、列表、归纳、对应、抽象等认知行为，所以与该教学活动匹配的作业目标也应包括以上认知行为。

《简易方程》单元承载着发展学生代数思维的重要任务，教材内容编排没有从现实情境直接跨越到字母表征，而是用文字表达来过渡，设计了从举例到用文字表达规律，再到用字母表示规律的认知路径，其进阶符合“具象化—形象化—抽象化”的学生抽象能力发展过程。单元作业设计也应遵循这条路径，对所有课时活动内容进行认知行为识别，以获得整个单元的认知活动规划。教师可以通过查阅2022年版课程标准和现行教材中与方程有关的内容，在知识与认知维度下整体分析单元内容，从认知活动的角度对要开发的作业进行标定，使其问题解决过程完全覆盖教材中出现的认知活动，确保所设计的作业在知识技能、思想方法和认知活动上与教材一致，从而实现通过作业发展学生核心素养的目标。下面是整个单元的认知活动规划表。

二、研判评价导向：从素养层面评估学习成果

培养学生的素养并确保素养目标达成是教、学、评的一致目标。学生学习成果的评估不能仅仅关注知识技能层面。评价作为检验学习的方式，应该以培养学生素养为导向，验证他们在多个层面上的素养达成情况。这种评价既能有效评估学生在实际情景中应用知识解决问题的能力，培养他们的数感、符号意识、模型意识、创新意识等核心素养，又能促使教师以素养培养为目标进行教学。教师设计作业目标时要以培养数学核心素养为导向，引导学生在学习中获得全面发展。实际操作中，教师可以从近年的创新试题中获得相关启发。

2022年版课程标准指出，在第三学段的教学中，学生应“能运用常见的数量关系解决实际问题，能合理解释结果的实际意义，逐步形成模型意识和几何直观，提高解决问题的能力”。长久以来，方程的考查方式都比较传统：命题者通常利用求解方程的题型考查学生的运算能力，或者利用方程应用题考查学生的建模能力，较少在灵活的问题情境中考查学生对方程概念的理解。为落实2022年版课程标准要求，当前的测评对方程的考查不再局限于常规的代数领域，而是倾向于在非常规、跨内容的背景下设计灵活的任务。以下题为例，该问题将展区中的桌椅抽象为几何图形，通过图形的摆放引导学生发现其中的等量关系，并用字母表示。这样设计打破了以往基于文字、表格描述问题情境的任务设计模式，具有创新性。

（1）该长方形区域的长可以用      式子表示。

（2）根据图中信息，用等式表示a，b，c满足的关系。

以上问题要求学生在图形情境中發现等量关系，侧重综合考查学生的观察、归纳等能力，引导学生采用举例、猜测等方法探究问题的本质，发现变化中的不变关系，并用字母表示这种关系。与传统的文字题相比，图形情境更加开放，更有利于考查学生能否从本质上理解等量关系。

以上典型试题的分析表明，指向素养的测试与传统的偏重考查知识与技能的测试在命题方向上存在明显差异。因此，在设定作业目标的过程中，教师要把握评价导向，让作业目标与评价导向一致，才能达到事半功倍的作业效果。

三、精准把握学情：从典型错误透析学习路径

从教材内涵、评价导向方面确定作业的大体方向后，作业设计需要与学生实际的学习情况相衔接。结合学情设计作业目标非常重要，为了做到这一点，笔者提供一种可参考的路径——分析学生的典型错误，透析错误背后的学习路径，未雨绸缪地设定作业目标。通过这样的分析，教师可以了解学生在学习过程中常犯的错误及出错原因，更好地把握学生的学习需求和问题所在，进而设计能够突破易错点和难点的作业。教师甚至可以将这些内容前置，作为教学任务，帮助学生突破学习难点。

例如，方程教学中，理解“等号”是重中之重。等号具有两重意义：从“过程”的角度看，等号表示运算的结果；从“结果”的角度看，等号表示两个式子之间的关系。大部分学生对前者是熟悉的，但对后者，即使中学生和大学生也有可能出现错误。例如，Herscovics等人在研究中发现，中学生容易在作答中错误地使用形如“[17n+12n+36=210=29n+36=210]”的连等式。又如，Clement在Algebra word problem solutions： Thought processes underlying a common misconception（《代数文字题解决方案：常见误解背后的思维过程》）中说明，即使是大学生，也会习惯性地用等号连接不相关的解答过程。

学生对等号的误解始于小学。由于受到算术运算的影响，学生经常错误地认为等号的意思是“答案是”，而难以将等号理解为“表示相等关系”。Falkner曾经利用判断题评价小学生对等号的理解情况，他在Childrens understanding of equality： A foundation for algebra（《儿童对等号的理解：代数的基础》）一文中举例，判断“[3+4=7]，[12-5=9]，[7=3+4]，[8+2=10+4]，[7+4=15-4]，[8=8]”中哪些式子正确时，一部分学生认为“[3+4=7]”是对的，但“[7=3+4]”是错的，因为这部分学生认为等式不能“倒”着写；还有学生认为“[8=8]”是错的，理由是虽然8的确等于8，但不能这样写。

对于以上错误概念，Asquith等学者在Middle School Mathematics Teachers Knowledge of Students Understanding of Core Algebraic Concepts： Equal Sign and Variable（《中學数学教师对学生理解代数核心概念——等号和变量的认识》）一文中提出建议：引入未知数这个概念之前，学生就需要正确理解等号的意义，这对于理解恒等变形与逆运算起关键作用，否则学生会在理解那些两边都有变量的方程时出现障碍。有研究者进一步指出，教师可以在教学过程中有意识地交换等号两边的内容，如将“[2x+3=5]”变换为“[5=2x+3]”，帮助学生更加灵活、深入地理解等号的意义。

总的来说，在作业目标的设定上，教师除了通过作答分析，发现学生学习中的典型错误，还可以通过查阅文献，了解学生出现相应错误的原因及其干预策略，这样才能进一步完善作业目标的设定，达到“未病先治”的教学效果。

经历从认知层面解读教材、依据评价导向确定任务类型、通过观察学生精准把握学情三个环节的作业目标设定，对于减轻学生负担和提高教学质量具有重要意义。这既有助于学生目的明确地学习，又为教师提供了更有效的评价工具，能推动教与学协同发展。

（曹辰系北京教育学院数学与科学教育学院数学系讲师）

责任编辑  刘佳