面向板料精准堆垛的线特征位姿标定方法

方归，刘怀广,b*

面向板料精准堆垛的线特征位姿标定方法

方归a，刘怀广a,b*

（武汉科技大学 a.冶金装备及其控制教育部重点实验室 b.机械传动与制造工程湖北省重点实验室，武汉 430081）

板料堆垛是现代流程工业生产中常见的生产环节，其堆垛质量影响着包装和运输安全。针对多边形板料自动堆垛中机械手抓取和对齐问题，提出一种基于网格筛选的线特征相机位姿标定方法，给出空间特征点的选择标准，解决因板料纹理不足带来的点特征精度下降的问题。首先通过检测特征点来表示待匹配线，然后利用基于三角网格的线特征构型筛选算法，获得精确的匹配线；再利用单应性矩阵求解获得转换矩阵，最后通过转换在线板料图像，获得实际抓取点和转换角度。通过桌面板料抓取实验和现场验证，重投影误差不超过2像素，1 m板料的堆垛误差为0.5 mm，证明了此方法在板料自动堆垛过程中针对特征检测和位姿估计问题的有效性。

位姿估计；特征检测筛选；网格划分；机械臂抓取堆垛

近年来，机器人在流程工业中应用越来越广泛，如钢板切割、玻璃制造等。这些行业在生产中，通常需要对产品进行抓取，并按要求堆垛，以便进行包装和运输[1]。将视觉与机械臂结合是实现高精度抓取堆垛任务的主要研究方向，而视觉抓取堆垛的核心就是板料的位姿估计和堆垛匹配问题。

对于工业环境下的位姿估计问题，主要采用基于模板匹配和特征映射2种方法[2]。在基于模板匹配的方法中，每个目标都会选择某具有代表性的物体图像作为模板，然后通过扫描特征匹配测试找到姿态。虽然该方法能够较好地响应弱纹理目标，但是其精度受到光照、遮挡和视角变换的影响较大，在实际应用中需要结合深度学习和传感器融合等技术来提高其准确性。基于特征映射的方法又分为基于点特征的目标位姿估计问题，即PnP问题（Perspective-n- Point）[3]，以及基于线特征的目标位姿估计问题，即PnL问题（Perspective-n-Line）[4]。前者根据已知特征点在目标坐标系（通常被称作世界坐标系）和图像坐标系下的不同表达，利用透视投影关系求得目标在这2个坐标系之间的变换关系。对于表面光滑、特征点较少的弱纹理物体，使用特征点的映射很难建立物体的位姿与特征之间的表征关系，采用基于线特征的目标位姿估计方法具有更好的鲁棒性，且特征数目和特征奇异值对它的影响较小。由此，文中利用PnL方法研究像素坐标系与机械臂坐标系之间的映射关系。

目前，利用PnL方法解决坐标系变换问题的方法有很多种。其中，直接线性变换（Direct Linear Transformation, DLT）方法[5]是一种非常直接的非迭代方法，在有足量空间参考直线情况下，其求解精度较高且简单有效，但在目标特征数目较少或纹理不足时其求解效果不理想。为了提高PnL算法的适用性，Mirzaei等[6]通过Cayley变换方式旋转矩阵，然后通过矩阵分解和合成的方式，将PnL位姿求解问题转换为最优化问题，最后通过矩阵合成技术求解最优化问题。由于Mirzaei的方法采用Cayley参数表示旋转矩阵，在求解过程中容易出现矩阵奇异值，导致求解的稳定性不好。与此同时，刘昶等[7]证明PnL问题解的数量与相机光心和直线的相对位置有关，该结论为应用直线特征估计单目视觉位姿提供了理论依据。

文中针对工业环境下带钢板料纹理不明显、特征少且对堆垛精度有较高要求的条件，提出基于线特征的板料位姿评估方法，以减小传统基于点特征进行位姿估计带来的转换误差，并通过搭建机械臂抓取实验平台，验证位姿的估计效果。

1 板料抓取任务模型

如图1所示，带钢经过开卷后，沿着辊道进入切割工位。切割机由支架支撑，根据排样切割出指定形状。通过相机对切割后的板料进行成像处理，并计算抓取位置和相对于第1块板料的位姿转换信息，然后驱动机器臂进行抓取，并根据位姿信息转换后堆垛。

图1 板料堆垛过程模型

1.1 坐标转换

在该模型中，主要存在4个坐标系：图像坐标系p-、相机坐标系c-ccc、世界坐标系w-www和机械手末端坐标系t-ttt。其中，世界坐标系以机器臂的底座为原点。机器臂抓取过程主要包括三次坐标转换。

1）相机坐标到图像坐标，该过程为小孔成像模型，见式（1）。

式中：为相机焦距；d、d为单个像素在或方向的实际物理尺寸；为2个方向的尺度偏差；0、0为相机坐标系原点在成像平面的投影坐标。以上参数组成了相机的内参矩阵1，该矩阵通过张氏标定[8]来获得。

2）从世界坐标转换到相机坐标，该过程为刚体变换过程，见式（2）。

式中：3×3为世界坐标系相对于相机坐标系的旋转矩阵；3×1为平移矩阵，它们通过组成4×4矩阵的形式表述外参矩阵2。在此模型中，因为相机和机器臂位置都不发生变化，因此2相对固定，主要通过P3L算法[9]来求解2。

3）从世界坐标系转换到机械手末端坐标系，该过程称为刚体变换过程，主要通过机器臂的示教来完成，见式（3）。

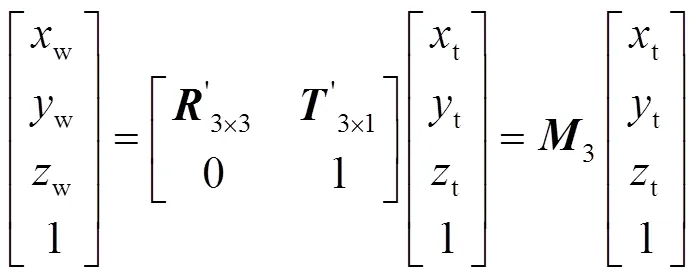
整个模型的算法流程如图2所示。

图2 算法流程

Fig.2 Algorithm flow

从图2中可以看出，小孔成像模型1的精度由相机本身决定，机械手末端坐标到世界坐标的转换矩阵3的精度由机械手示教精度决定，因此从世界坐标到相机坐标的转换矩阵2很大程度上决定了堆垛精度。

1.2 P3L算法

本文研究位姿的估计方法针对特征数目较少的弱纹理目标，采用一种基于线特征的P3L（Perspective-3-Line）算法[10]，利用世界坐标系中的3条参考线和像平面上的投影来求解转换矩阵。建立同一块板料在机械臂坐标系和像素坐标系下的不同表达，在完成线特征匹配后，便可以通过位姿估计构建2个坐标系之间的联系。

如图3所示，世界坐标通过旋转（Rotation）、平移（Translation）变换为像素平面坐标。AB=(AB,A,B)，表示一条世界坐标系下的线特征。AB表示这个线特征的标准化向量。A、B表示该线特征的板料角点。AB=(ab,a,b)，表达该线在像素坐标系下的特征。根据直线AB在2个坐标系的约束条件，将2的旋转矩阵参数化，见式（4）。

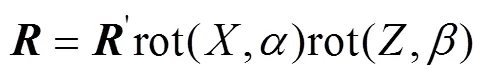
图3 线特征的匹配关系

Fig.3 Matching relation of line features

式（3）中平移向量可以通过平面特征点ab垂直于求解得到，见式（5）。

式中：为像素平面的法向量。

2 基于网格筛选的线特征获取

空间中的线由2个空间点来确定，因此首先需要获得待抓取平面的关键点。根据多边形板料的边缘线性关系，把板料边缘角点作为关键点来求解线特征，从而将线特征获取问题转换为关键点提取问题，以提高求解精度。

2.1 关键点提取

式中：为像素位置；P为ORB算法处理该区域中心像素点的阈值。

完整的关键点提取流程如图4所示。这种自适应的阈值设置方法解决了整幅图像因阈值取值经验化所致的关键点漏检问题，最终关键点提取结果如图5所示。

2.2 基于网格筛选的线特征评价

在完成关键点的提取后，可任取2个关键点组成线特征，结合示教得到它在机械臂坐标系下的物理坐标，即可求解抓取平面与机械臂之间的转换关系。由于P3L算法求解与选择空间线的构型紧密相关[13]，

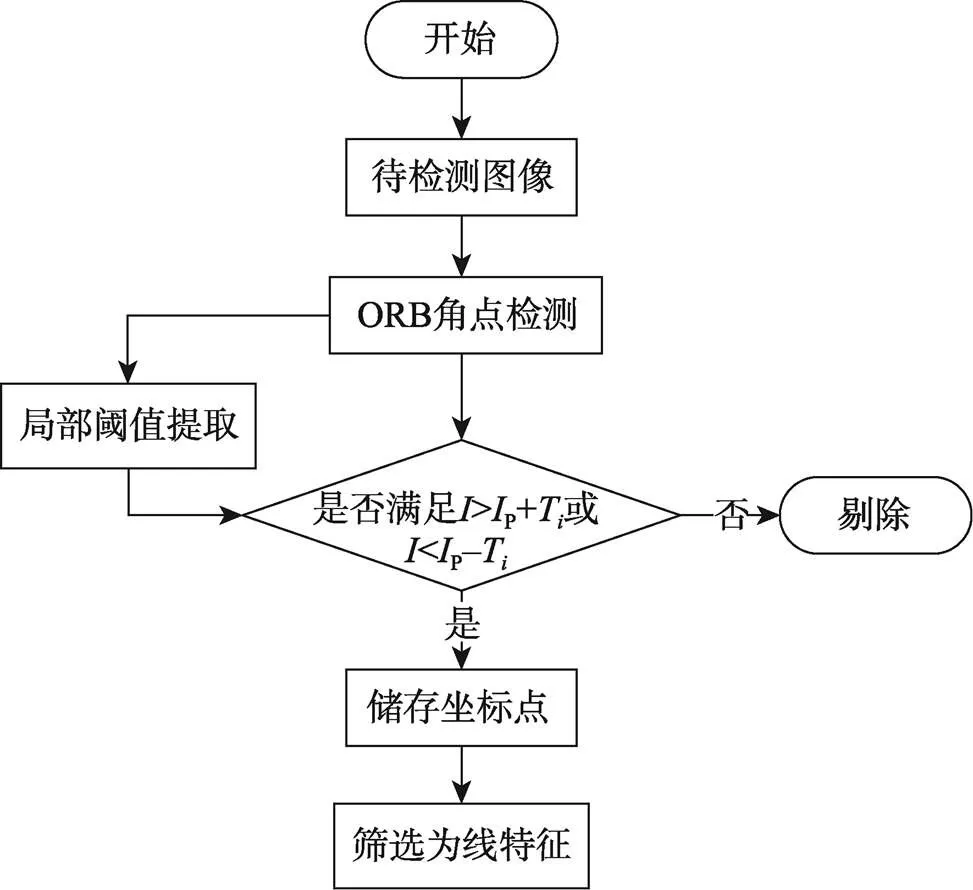
图4 关键点提取流程

图5 ORB关键点检测结果

P3L求解的精度会随着选择线特征的交点数量及它们在空间内的位置关系而变化，因此选择合适的关键点组成线特征十分重要。这里将关键点集划分为三角网格，并对不同网格进行评价，选出最合适的空间线构型。

针对提取的关键点，可以利用逐点插入法形成三角网格。如果不加以限制，则会使网格呈几何级数增长。为了保证划分的三角网格最大化和具有唯一性，这里引入空圆特性，即三角形的外接圆内部不再包含任意一个其他三角形顶点，则该三角网格具有空圆特性（如图6中的△、△）。空圆特性保证了三角网格的唯一性，并保证网格内每个角尽可能大，使得该三角网格对应的线特征构型交点数量最多，且空间位置最理想。

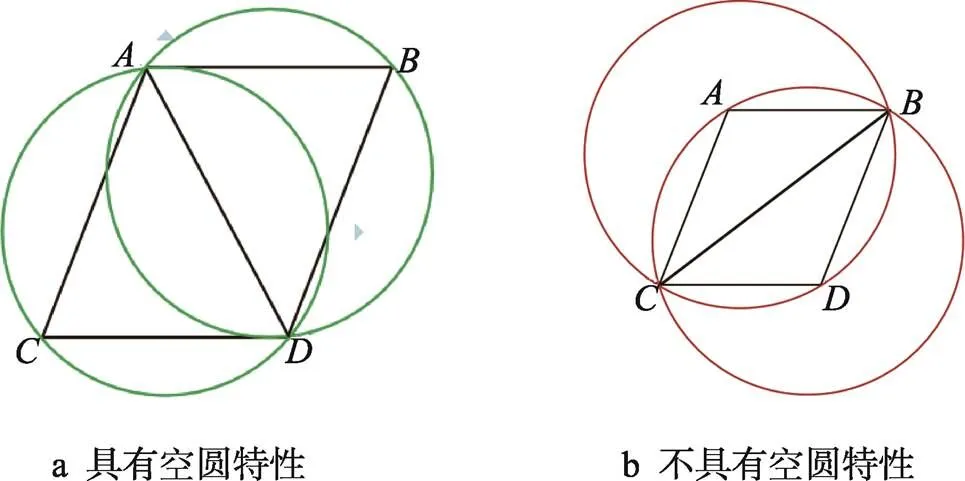
图6 平面点集的2种划分方式

针对提取的关键集形成后的三角形，利用空圆特性检测，剔除公共边，形成最理想的三角网格划分方案，如图7所示。以4个平面点集{1,2,3,4}为例，具体步骤如下。

1）设计任意的大三角△，包含所有待处理的平面点集{1,2,3,4}，将所有点当作待插入点逐个插入。

3) 更新:经过分裂步骤产生子集的某些整体特征可能与原始数据并不一致，为了保持数控机床热误差数据的这些整体特征，需要一个更新的过程。将更新过程用算子U来代替，其过程为：

2）当插入第1个点1时，直接与△各顶点相连。

3）在插入2点时，检测已形成的三角形的外接圆是否包含2点，并将包含2的外接圆对应的三角形的公共边删除，然后以2点为中心与包络它的多边形1各顶点相连。

4）在插入3、4时，各重复1次步骤3），当所有点集都被检测时，删除包含大三角形顶点的全部三角边。

图7 逐点插入法生成网格

在划分过程中，每生成1个网格便提取其3个顶点1(1,1)、2(2,2)、3(3,3)，并计算该网格的面积，见式（7）。

对所有关键点进行网格划分完毕后，提取面积最大的三角网格作为目标提取线特征Smax，如图8中的红色三角网格所示。由于该算法划分出的三角网格都具有使最小角最大化的特性，因此该目标网格最接近正三角形，是构型最饱满的三角形，它对应的3条线特征最满足P3L算法精度的特征。

在提取最大三角形后，利用三角形的3条边形成标定平面，建立像素坐标和物理坐标的转换模型，见式（3），并结合式（5）完成相机的姿态标定。

3 结果与分析

3.1 位姿精度比较

为了研究直线构型对位姿估计精度的影响，这里设计了1组对照实验。以PNP算法求解得到的旋转矩阵为对照，对各种构型情况下的P3L算法求解结果进行比较，如图9所示。为了保证结果的鲁棒性，先对某图像进行足量的特征提取，然后使用PNP算法[14]求解这些特征点的位姿，得到旋转矩阵，把该结果当成近似正确的位姿解，记作true。针对每种构型，使用P3L算法计算得到相应的旋转矩阵，记作est。通过比较旋转矩阵间欧氏距离的模（即矩阵差值的范数）来度量不同构型下的位姿精度，模越小，表明越接近PNP算法的近似解，对应的P3L算法位姿精度越高，见式（8）。

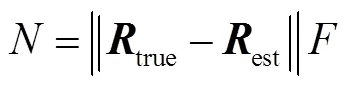
由表1的结果可知，P3L算法求解位姿的精度随着线特征在空间中交点数目的减少而降低。当线特征构型尽可能接近正三角形时，位姿精度最高，符合通过网格筛选算法提取线特征的要求。

在此利用前文方法采集的数据（图10），蓝色三角形为经过构型筛选的3条线特征，把它们作为输入进行基于线特征的位姿估计，黄色角点是随机挑选的特征点且基本满足奇异值和数量要求，把它们作为输入进行基于点特征的位姿估计。使用P3L算法和传统的PNP算法分别对它们在位姿估计精度误差方面进行分析和比较。

表1 位姿结果比较

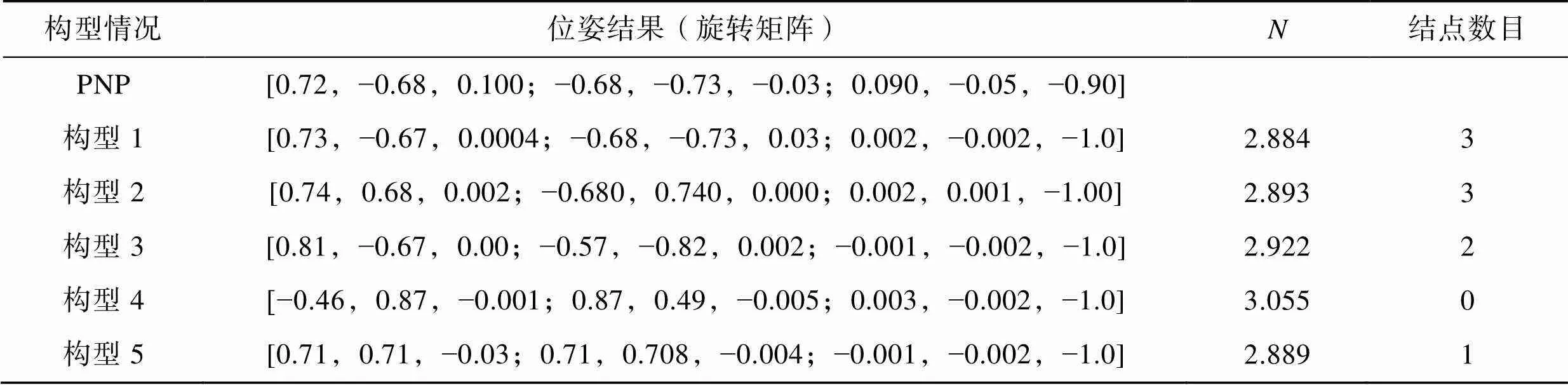
Tab.1 Comparison of pose results

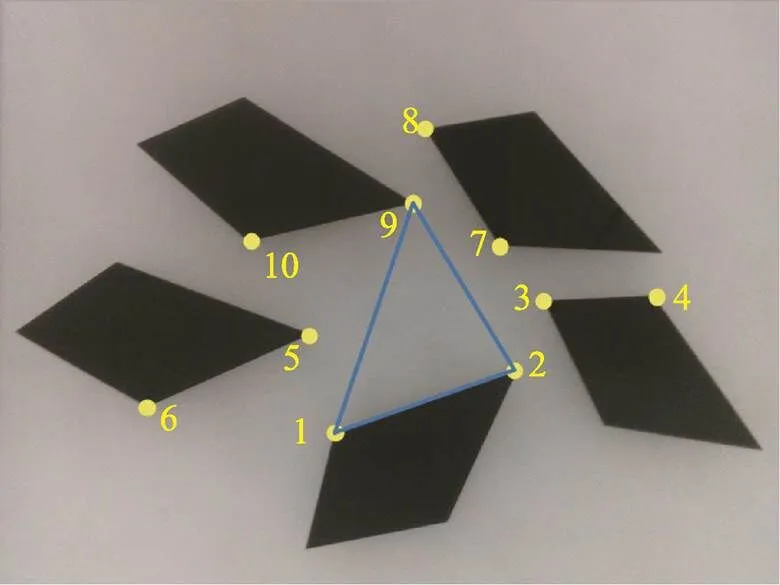
图10 点线特征处理结果

这里采用的评价标准为重投影误差[15]，将两者估计得到的位姿结果带回原始的投影公式，重新计算板料角点从世界坐标系投影到像素坐标系的新的像素坐标，即最开始采用ORB算法提取到的关键点坐标，通过比较重投影误差来评价2种方法的效率和精度，见表2。

将已知世界坐标系点重投影为像素坐标系点的表达式，见式（9）。

式中：为重投影前像素坐标系的二维坐标。

由表2和图11可知，采用P3L算法，对角点的重投影误差为1.17像素；采用PNP算法，对角点的重投影误差为3.66像素。由此可见，P3L算法在弱纹理目标特征数目较少的情况下相较于PNP算法，其精度更高、实用性更强。

表2 2种算法重投影结果及误差

Tab.2 Projection results and errors of two algorithms

图11 重投影效果比较

3.2 机械臂抓取堆垛验证

如图12所示，通过任意放置的板料来模拟实际生产线上的场景。提取板料在像素坐标系中各个特征角点后，使用Dobot Magician机械臂自带的示教功能获取各角点在世界坐标系中的坐标。为了让机械臂实现精确的堆垛功能，还需要获得板料在世界坐标系内摆放位置的基本信息。对采集的图样进行二值化处理后，提取板料的轮廓信息，进行简单的轮廓筛选后，便可将板料进行分割和定位。使用最小矩形包络算法将所有板料的抓取基准进行统一。考虑到实际场景中板料面积较大，抓取后上下晃动会影响堆叠精度的问题，以机械臂的抓取点为板料的质心，使用图像矩的方法对图像像素进行加权平均，从而找到板料的质心。

将得到的堆垛信息经旋转平移变换，变换为世界（机械臂）坐标系下的坐标，如表3所示。

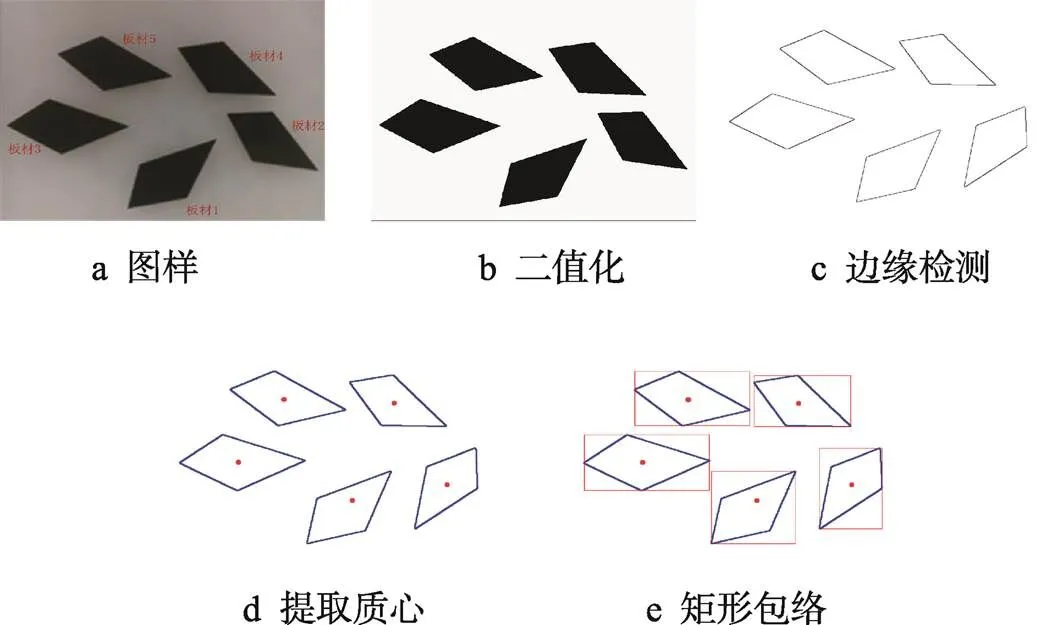
图12 板料堆垛信息获取

表3 堆垛信息变换

Tab.3 Stacking information transformation

在完成基本数据处理工作后，通过调用机械臂的动态链接库，将数据全部输入机械臂的控制程序中，执行板料的抓取堆垛工作。桌面机器臂算法验证过程如图13所示。

图13 桌面机械臂抓取实验

3.3 生产现场实验验证

根据文中算法的流程，类比实验中的亚克力板料及桌面型机械臂，开发了一套板料堆垛的机器人控制系统，并应用于浙江某企业，如图14所示。结果表明，在板宽为1 m的情况下，堆垛精度在0.5 mm以下，满足生产要求，验证了文中算法的有效性。

4 结论

在生产线上，板料纹理特征少且取样背景单一的特点决定了精准求解此类目标位姿精度的难度。结合实际生产需求，提出了只需要较少特征数目就能准确估计位姿的方法，在此基础上对平面点集数据进行了网格划分处理，保证了位姿求解的稳定性。经实验验证，该方法相较于传统方法，在解决板料堆垛问题方面具有更好的效果，且堆垛精度满足生产需求。在后续工作中，针对重叠遮挡对象的分割，进一步研究解决三维空间复杂目标的堆垛问题。

[1] 袁浩. 机器人在物流仓储中的应用现状与发展趋势分析[J]. 物流技术, 2022, 41(12): 11-14.

YUAN H. Current Status and Development Trend of Robot Application in Logistics and Warehousing[J]. Logistics Technology, 2022, 41(12): 11-14.

[2] 周芮, 刘延芳, 齐乃明, 等. 面向空间应用的视觉位姿估计技术综述[J]. 光学精密工程, 2022, 30(20): 2538-2553.

ZHOU R, LIU Y F, QI N M, et al. Overview of Visual Pose Estimation Methods for Space Missions[J]. Optics and Precision Engineering, 2022, 30(20): 2538-2553.

[3] PAN S Y, WANG X M. A Survey on Perspective-n-Point Problem[C]// 2021 40th Chinese Control Conference (CCC). IEEE, 2021: 2396-2401.

[4] YU Q D, XU G L, WANG Z S, et al. An Efficient and Globally Optimal Solution to Perspective-n-Line Problem[J]. Chinese Journal of Aeronautics, 2022, 35(3): 400-407.

[5] ABDEL-AZIZ Y, KARARA H, HAUCK M. Direct Linear Transformation from Comparator Coordinates into Object Space Coordinates in Close-Range Photogrammetry[J]. Photogrammetric Engineering & Remote Sensing, 2015, 81(2): 103-107.

[6] MIRZAEI F M, ROUMELIOTIS S I. Globally Optimal pose Estimation from Line Correspondences. In: IEEE International Conference on Robotics and Automation, Shanghai, China: IEEE Press, 2011: 5581-5588.

[7] 刘昶, 朱枫, 欧锦军. 基于三条相互垂直直线的单目位姿估计[J]. 模式识别与人工智能, 2012, 25(5): 737-744.

LIU C, ZHU F, OU J J. Monocular Pose Determination from Three Perpendicular Lines[J]. Pattern Recognition and Artificial Intelligence, 2012, 25(5): 737-744.

[8] ZHANG Z. A Flexible New Technique for Camera Calibration[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(11): 1330-1334.

[9] XU C, ZHANG L L, CHENG L, et al. Pose Estimation from Line Correspondences: A Complete Analysis and a Series of Solutions[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(6): 1209-1222.

[10] 王平, 何卫隆, 张爱华, 等. EPnL: 一种高效且精确的PnL问题求解算法[J]. 自动化学报, 2022, 48(10): 2600-2610.

WANG P, HE W L, ZHANG A H, et al. EPnL: An Efficient and Accurate Algorithm to the PnL Problem[J]. Acta Automatica Sinica, 2022, 48(10): 2600-2610.

[11] RUBLEE E, RABAUD V, KONOLIGE K, et al. ORB: An Efficient Alternative to SIFT or SURF[C]// 2011 International Conference on Computer Vision. IEEE, 2011: 2564-2571.

[12] OTSU N. A Threshold Selection Method from Gray-Level Histograms[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1979, 9(1): 62-66.

[13] 赵汝进, 张启衡, 左颢睿, 等. 一种基于直线特征的单目视觉位姿测量方法[J]. 光电子激光, 2010, 21(6): 894-897.

ZHAO R J, ZHANG Q H, ZUO H R, et al. A Mono-Vision Method of Measuring Pose Based on Line Features[J]. Journal of Optoelectronics Laser, 2010, 21(6): 894-897.

[14] LEPETIT V, MORENO-NOGUER F, FUA P. EPnP: An Accurate O(n) Solution to the PnP Problem[J]. International Journal of Computer Vision, 2009, 81(2): 155-166.

[15] 陈天择, 葛宝臻, 罗其俊. 重投影优化的自由双目相机位姿估计方法[J]. 中国光学, 2021, 14(6): 1400-1409. CHEN T Z, GE B Z, LUO Q J. Pose Estimation for Free Binocular Cameras Based on Reprojection Error Optimization[J]. Chinese Optics, 2021, 14(6): 1400-1409.

Line Feature Pose Calibration Method for Accurate Sheet Stacking

FANG Guia,LIU Huaiguanga,b*

(a. Key Laboratory of Metallurgical Equipment and Its Control, Ministry of Education, b. Hubei Provincial Key Laboratory of Mechanical Transmission and Manufacturing Engineering, Wuhan University of Science and Technology,Wuhan 430081, China)

Sheet stacking is a common production link in the industrial production of modern process, and its stacking quality affects packaging and transportation safety. Aiming at the problem of robot arm grasping and alignment in automatic stacking of polygonal sheets, the work aims to propose a method for calibrating the pose of line feature camera based on mesh screening and put forward the selection criteria of spatial feature points to overcome the problem of point feature accuracy decline caused by insufficient sheet texture. Firstly, the line to be matched was represented by detecting feature points, and then the accurate matching line was obtained by the line feature configuration screening algorithm based on triangular mesh. Next, the transformation matrix was obtained by solving homography matrix, and finally the actual grasping point and transformation angle were obtained by transforming the online sheet image. Through the desktop sheet grabbing experiment and field verification, the error of re-projection was less than 2 pixels, and the error of 1 meter sheet stacking was 0.5 mm. It is proved that this method is effective for feature detection and pose estimation in the process of automatic stacking of sheets.

pose estimation; feature detection and screening; grid division; mechanical arm grasping and stacking

TB485.3

A

1001-3563(2024)09-0185-08

10.19554/j.cnki.1001-3563.2024.09.024

2023-10-23

国家自然科学基金（52272377）