主线视角下探析双曲线渐近线的相关优美性质

广东省惠州仲恺中学(516229) 陈伟流

自“三新”(新课标,新教材,新高考)背景的课程改革推进实施以来,高考命题已悄然从能力立意转向以为素养导向,表现为试题深入考查基础知识和基本能力,彰显了国家人才选拔和支持“双减”落地的显著特点,对学生的数学运算,逻辑推理,数学抽象,直观想象等核心素养的考查既深入又全面,凸显了数学学科强大的基础性作用.具体到解析几何模块中,以双曲线为载体背景的试题已多次现身于高考真题或模拟试题中,有效地打破了以往常规的命题套路,其中以渐近线为核心考点的试题涵盖了与距离,中点,面积等关联的定值定点问题,既传承经典,又常考常新,凸显了双曲线区别于椭圆及抛物线的独特魅力,充分考查了学生问题解决的思维品质和思维过程.为此,笔者以双曲线的渐近线为关联主线,通过探析相关典型的优美性质,旨在厘清知识的来龙去脉,明晰其底层逻辑,提升学生的解题认知能力和应用能力.

1 性质探析

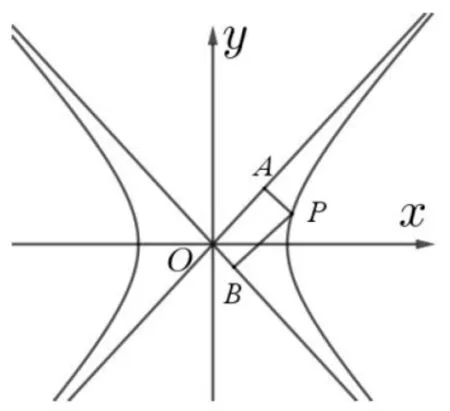
图1

性质2已知不过原点的直线交双曲线=1(a,b ＞0)于A,B两点,交两条渐近线于C,D两点,其中A,C恒在同一象限,则恒有|AC|=|BD|.

图2

设lAB的方程为x=my+t.因lAB与双曲线相切,故由①式知

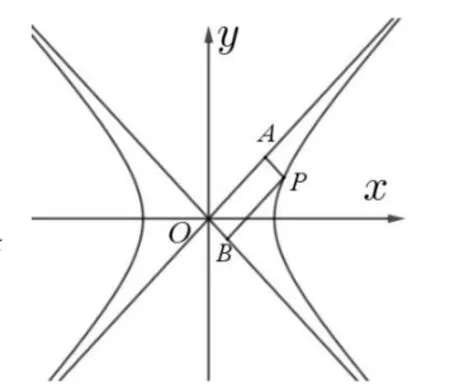
图3

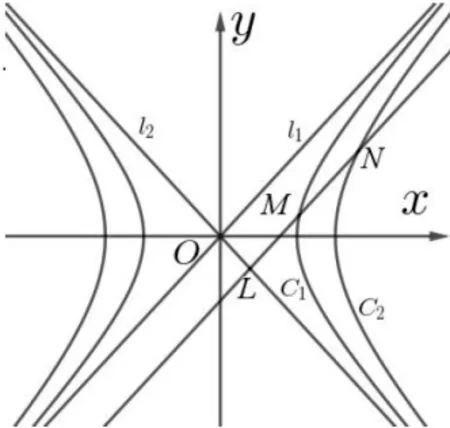
图4

图5

注若两双曲线有相同的渐近线且焦点位置相同,因离心率相同,称二者是相似双曲线,性质5 及性质6 则是从本质上揭示了相似双曲线间的一组优美性质.

性质7已知直线l1,l2是双曲线=1(a,b ＞0)的两条渐近线,动直线交l1,l2于A,B两点,过AB的中点M作l1,l2的平行线交双曲线于C,D两点,则AB//CD.

综上,AB//CD.

注通过性质7 的探索知: 直线AB截双曲线渐近线所得弦长的中点是决定平行关系的关键因素,与直线AB是否过定点并无关联.

2 应用提升

以双曲线渐近线为核心考点的解析几何试题涵盖长度,面积等度量问题及点线关系等位置问题,综合考查学生的运算求解,空间想象等关键能力,对数学运算,逻辑推理,直观想象等核心素养有较高的导向要求.为此,笔者列举几道经典模拟试题,供读者参考借鉴,以期为高考备考提供一定的借鉴.

题1(2023 年湖南岳阳统考三模试题)已知点(1,2)在双曲线E:=1 (a ＞0,b ＞0) 的渐近线上,点A(-3,2)在E上,直线l交E于B,C两点,直线AB与直线AC的斜率之和为0.

(1)求直线l的斜率;

(2) 若M为双曲线E上任意一点,过点M作双曲线的两条渐近线的平行线,分别与两条渐近线交于点P,Q,求ΔMPQ的面积.

答案(1)直线l的斜率为6;(2)ΔMPQ的面积为4,过程略.

(1)求双曲线C的标准方程;

(2) 设直线l是曲线C在点P(x0,y0) 处的切线,且l分别交两条渐近线l1,l2于M,N两点,O为坐标原点,求ΔMON的面积.

(1)当k变化时,求点M的轨迹方程;

(2)若l与双曲线E的两条渐近线分别相交于C,D两点,问: 是否存在实数k,使得A,B是线段CD的两个三等分点? 若存在,求出k的值;若不存在,说明理由.

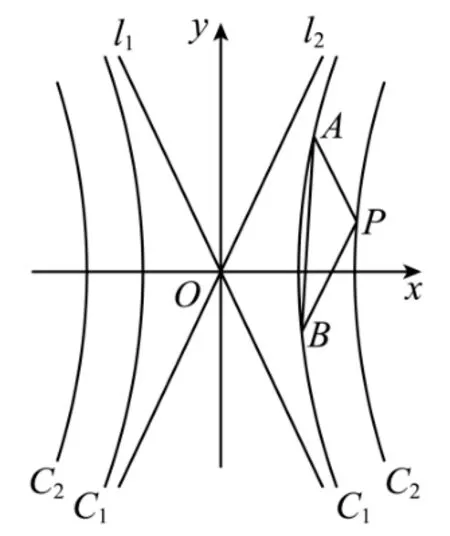
图6

3 结束语

《普通高中数学课程标准》(2017 年版2020 年修订)》在教学内容的设计上强调了三个关注理念: 即关注同一主线内容的逻辑关系,关注不同主线内容间的逻辑关系,关注不同数学知识所蕴含的通性通法,数学思想[2].以双曲线渐近线的主线思想为例,其内容涵盖了与长度、面积关联的定值定点内容及平行,垂直,相切等位置关系问题,考查了直曲联立法,点差法等解析几何通性通法思想.在渐近线主线视角的光芒下,凝聚其优美性质的知识宝库可谓是博大精深,包罗万象,所以在一线教学中,教师要以知识主线统领的视角审视教学内容,厘清不同知识在底层逻辑的区别与联系,如此才能为学生带来层次分明,亮出突出,联系紧密的课堂内容,以培养数学抽象的高阶思维和整体认知的数学观,促进高考备考的提质增效[2].