三次函数零点问题的探究与拓展

2024-05-17广东省广州市广州中学510630陈俊儒

中学数学研究(广东) 2024年7期

广东省广州市广州中学(510630) 陈俊儒

三次函数是高中数学中的重要函数模型,频繁见于普通高中教科书(人民教育出版社) 选择性必修二.教材第99 页安排了三次函数的拓展探究内容: 利用信息技术工具,根据给定的a,b,c,d的值,可以画出函数f(x)=ax3+bx2+cx+d(a0)的图像,当a=-4,b=1,c=5,d=-1 时,f(x)的图像如图1 所示.改变a,b,c,d的值,观察图像的形状:

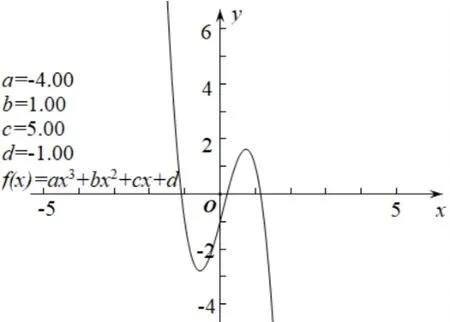
图1

图5

(1)你能归纳函数f(x) 图像的大致形状吗? 它的图像有什么特点? 你能从图像上大致估计它的单调区间吗?

(2)运用导数研究它的单调性,并求出相应的单调区间.

从教材编排可见,三次函数在函数模型中占据重要的地位,教学中应引导学生利用导数工具研究三次函数的图像与性质,把握研究三次函数与其他基本函数的异同.三次函数也是高考的高频考点,考察内容以三次函数的切线,对称性,极值与最值,零点问题为主,其中零点问题出现次数较多,难度较大,本文以2020 年全国III 卷第21 题为例,深入探究三次函数的图像与性质,并对三次函数零点间的关系延伸拓展.

以上是解决此高考题的两种常见方法.另外,我们面对函数的零点问题时,经常转化为方程的根进行解决,那么三次函数的零点问题能否转化为三次方程的根与系数关系并结合三次函数图像进行问题解决?

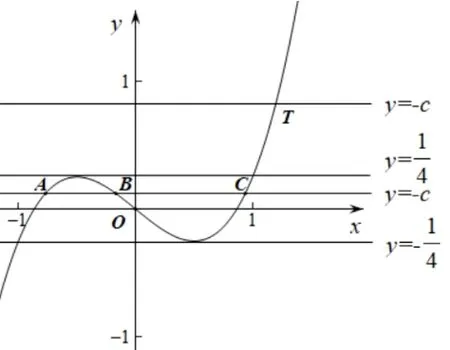
图2

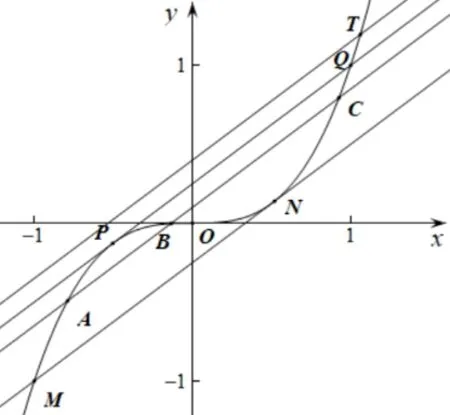
图3

图4

2020 年全国高考III 卷理科第21 题正是根据结论1 进行的特殊化命题.另外,既然三次函数的三个零点都是有界的,那么零点之间的距离也应该是有界的,能否得出最大和最小零点距离的取值范围?

由以上题目解答过程,可知三次方程韦达定理,推论1、2 和结论1、2、3,不仅给出了三次函数的零点与系数的数量关系,而且刻画了直线与三次函数相交(相切)时交点(切点)与对称中心的位置关系,是三次函数对称性的另外一种体现,同时还明确了三次函数在上下平移过程中零点的有界性和零点间距离的最值,这是三次函数零点的显著特征,在高考或高考模拟试题中常以上述推论或结论为背景进行命题.

题3(2024 年佛山市普通高中教学质量检测一第4 题)已知f(x)=(x+1)(x+a)(x+b)为奇函数,则y=f(x)在x=0 处的切线方程为( ).

A.x+y=0 B.x-y=0

C.3x+y=0 D.3x-y=0

解析因为三次函数f(x)=(x+1)(x+a)(x+b)对称中心为原点,所以-1-a-b=0,又因为f(0)=ab=0,所以a=0,b=-1 或a=-,b=0,所以f(x)=x(x+1)(x-1),k=f′(0)=-1,切线方程为x+y=0.答案为A.

题4(2021 年全国高考乙卷文科第21 题) 已知函数f(x)=x3-x2+ax+1.

(1)讨论f(x)的单调性;

(2)求曲线y=f(x)过坐标原点的切线与曲线y=f(x)的公共点的坐标.

(2)设过原点的切线l:y=kx,切点A横坐标为x0,直线l与曲线公共点的另一个交点横坐标为x1,由推论2 可得2x0+x1=1,根据三次函数韦达定理可得,解得x0=1,x1=-1,故公共点横坐标为1 或-1.

题5(2016 年天津高考理科第20 题) 设函数f(x)=(x-1)3-ax-b,x ∈R,其中a,b ∈R.

(1)求f(x)的单调区间;

(2) 若f(x) 存在极值点x0,且f(x1)=f(x0),其中x1x0,求证:x1+2x0=3.

(2)f(x)=(x-1)3-ax-b的对称中心横坐标为1,根据推论1 可得x1+2x0=3.