丰盈探索过程?把握规律本质

尤启飞

【摘 要】“间隔排列”是学生首次在复杂、现实的情境中认识规律，作为“探索规律”专题活动的“种子课”，通过丰富观察素材、问题驱动探究、优化探究作业三大策略，帮助学生把握间隔排列规律的本质，感悟一一对应思想。

【关键词】“间隔排列” 规律本质 一一对应

一、叩問——学之困，有何难

“间隔排列”是苏教版数学三年级上册“探索规律”专题活动的教学内容。此前，学生积累了许多探索数、图、算式规律的经验，但通过观察复杂现象、现实情境认识规律尚属首次。在规律探索过程中，明确规律排列和数量之间的逻辑关系，对学生来说，有一定的困难。

学前调查及几次试教结果表明，学生对间隔排列现象的认识不够透彻，部分学生窄化了对间隔排列的认识—“只有开头和结尾是同一种物体，才是间隔排列”；部分学生缺乏“为什么两种物体数量相差1”的深入思考，很难深刻理解间隔排列规律的本质，感悟一一对应的数学思想方法，只能机械记忆规律，套用规律解决问题。

作为“探索规律”专题活动的种子课，如何促使学生主动分析、理解间隔排列的规律本质？如何引导学生感悟一一对应的思想及作用？如何培养学生的探索意识，积累探索规律的活动经验，实现“种子课”的力量？为突破上述问题，笔者再次开展了教学实践。

二、实践——学之难，何以破

（一）丰富观察素材，外显规律特征

教材提供的三组物体均是两端物体多1的情况，单一、特殊的观察素材可能窄化学生的规律认识。因此，在实践中，笔者对三组间隔排列物体的数量进行适当的调整，并增加一组黄花和红花一一间隔排列的素材。四组物体为探究间隔排列规律提供了丰富、全面的观察素材，将间隔排列现象的本质特征外显，便于学生在观察、对比的过程中明确间隔排列现象的形式特征，也为后面分析两种物体间的数量关系奠定了良好的基础。

【教学片段1】

1.初步观察，感知规律特点

欣赏蓝红珠串，说说珠串的规律（图略）。

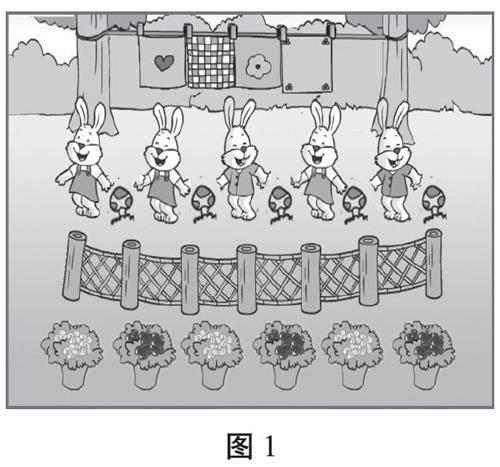
师：小兔乐园里有像珠串那样有规律排列的物体吗？它是怎样排列的？（如图1）

（学生回答略）

师：想一想，四组物体的排列有什么共同的规律？

生1：它们一般都有两种物体，两种物体为一组，一组一组排列的。

生2：他们都是一个隔着一个排列的。

师：像这样，两种物体一个隔着一个排列，叫作一一间隔排列。

2.画一组间隔排列

师：用你喜欢的方式，画一组间隔排列。

教师展示学生的不同作品，引导其他学生欣赏并判断是否是间隔排列。

四组素材中，兔子和蘑菇，黄花和红花，是两端物体不同的间隔排列；夹子和手帕，木桩和篱笆是两端物体相同的间隔排列。通过对四组素材的观察、比较和讨论，学生主动发现一一间隔排列现象，总结间隔排列物体的特征。接着，教师呈现学生用图形、颜色、符号等创造的多种间隔排列作品，在观察与辨析中，不断丰富学生对间隔排列现象的认识，最终形成间隔排列规律的表象。

（二）问题驱动探究，聚焦规律本质

问题驱动有利于发挥学生学习的主体性。具有驱动效应的问题，由易到难，从现象到本质，形成有机链条，引领学生的思维不断走向深入，聚焦间隔排列规律的本质。“探究开始，关于一一间隔排列现象，你还想研究什么？”这个问题的提出本着尊重学生，以学生为中心的原则，激发学生的问题意识和求知欲望。“比一比每组两种物体的数量，你发现了什么？”是将学生对规律的研究方向从具象的描述层面上升到抽象的数量层面。“为什么间隔排列中两种物体的数量有时相等，有时相差1？”可以促使学生去探究更具思考力的“为什么”，也就是产生现象的原因，这样学生的思维就能顺利聚焦规律的本质。“什么时候数量相等，什么时候数量相差1呢？”可以引导学生在基础的层面上理解规律的本质。

【教学片段2】

1.初步探究，发现数量关系

师：刚才，同学们通过观察，发现了间隔排列的规律，关于一一间隔排列，你还想研究什么？

生1：我想研究串100个蓝珠子，到底需要多少个红珠子？

生2：我想知道间隔排列中两种物体的个数有什么关系？

师：看来，大家都对个数有兴趣，那我们先来研究数量。

（研究过程略）

要求：比一比两种物体的数量，说一说你发现了什么？

（学生发现过程略）

2.深化探究，感悟一一对应思想

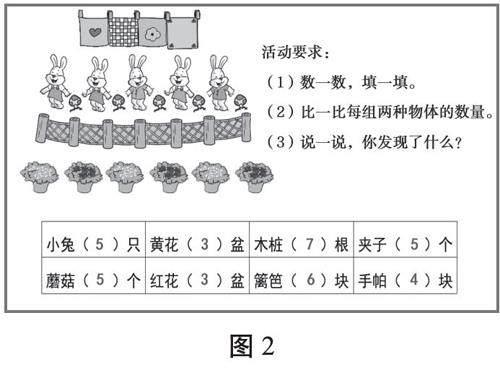
师：通过比较，我们发现间隔排列中两种物体数量的关系，有时候相等，有时候又相差1。你们还想研究什么？（如图2）

生1：为什么会有这种现象呢？

生2：到底什么时候相等，什么时候相差1呢？

师：好，我们依次来研究。

【教学片段3】

研究1：为什么两种物体有时数量相等，有时相差1？

生1：我用圆圈，将小兔和蘑菇圈成一组。一组一组圈下去，正好圈完，没有剩余，黄花和红花是一组，一组一组圈下去，也没有剩余，所以数量相等。

生2：我是一个夹子对应一块手帕，一组一组连一连，最后剩下了一个夹子。一根木桩对应一块篱笆，一组一组连下去，剩下一根木桩，因此数量相差1。

……

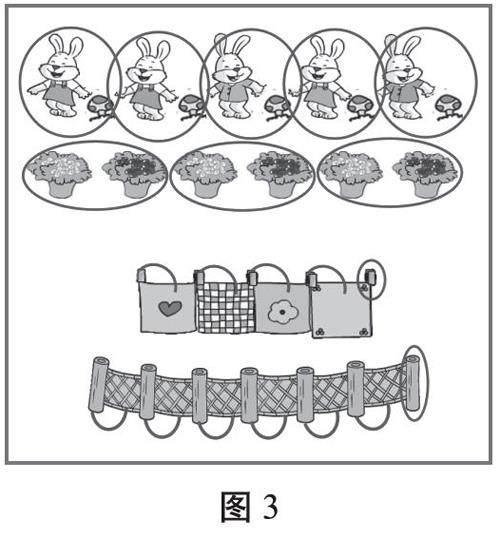
研究2：什么时候数量相等，有时相差1？

生：只要看两端的物体就可以了。如果两端的物体不同，说明正好一一对应，如果两端物体相同，如都是夹子，那一定少了一块手帕，数量就会相差1。（如图3）

在学生发现间隔排列规律后，教师通过问题引领学生主动关注数量。有了表格的对比观察，学生初步探究得出两种物体的数量关系。接着，学生的思维顺利聚焦核心问题“为什么有时相差1，有时相等”，教师顺着学生的思路，引导学生去探究产生现象的原因，并让学生用圈一圈、连一连的方式分析原因，体会一一对应思想，逐步将两端物体的特征与物体数量的关系勾连起来。最后学生主动探究“什么时候数量相等，什么时候相差1”，在深度观察、对比分析中，关注到“两端物体”，逐步聚焦规律本质，深刻理解规律。

（三）优化探究作业，内化规律本质

作业的教学功能与评价功能，是探究规律教学不可忽视的一部分。优化探究作业，巧妙利用变式练习，能够促使学生更加精准、深刻的理解和把握间隔排列规律的本质。

本节课，笔者设计了两项探究作业，将生活问题抽象成数学问题，使学生在自主探究、解决问题的过程中，提炼、丰富对一一间隔排列的认识，内化一一间隔排列的规律本质。

【教学片段4】

作业1：小小预言家（如图4）

师：猜猜谁的个数多。（依次出现）

师：遮住了一部分，还能知道谁的个数多吗？

生：开头是蓝珠，结尾是红珠，两端不同，一一对应，数量一样。

师：第四串呢？有的同学有些犹豫？

生：一样多，前面都是蓝红蓝红一一对应的。

生：后面盖住了，不知道另一端是什么，不能确定。

师：那怎么办？

生：只要看见最后一颗就可以。最后一颗是蓝色，那就是蓝色多，最后是红色，那就是一样多。

作业1蕴含了知识的基础应用、突破无限、拓展延伸三个层次的活动，指向在不同情境下，对间隔排列规律中数量关系的考察。在学习前两组时，基础较弱的学生，可以借助数一数的方法进行判断。第三组促使学生主动应用间隔排列的规律进行判断。第四组，将难度拔高，珠子的个数从有限走向无限，引导学生利用一一对应思想去思考，紧扣知识核心“两端相同”“两端不同”，进行正确判断，内化对规律数量关系的认识与理解。

【教学片段5】

作业2：小小设计师（如图5）

教师出示设计要求（1）。

生1：我设计的开头和结尾都是蓝珠，红珠只要9颗。

生2：我设计开头和结尾都是红珠，需要11颗。

生3：开头蓝珠，结尾红珠，需要10颗。

生4：我设计成项链，围成一圈，红珠个数也是10颗。

生5：其实，如果把项链剪开，拉直，他就是两端不同的间隔排列。

学生独立完成设计要求（2）。

生1：我设计了两个蓝珠，两个红珠，这样排列下去。

生2：我是按照一个蓝珠，两个红珠排列下去。

……

作业2是一道开放性的作业。设计要求（1）中，学生设计符合题目要求的间隔排列的项链送给妈妈，激发学生的研究兴趣。借助自主画一画的体验活动，呈现出四种不同的间隔排列，帮助学生感知红珠子个数的不确定性，进一步完善学生对一一间隔排列的两种物体的数量关系的认识，加深对一一对应这一数学方法的体验。设计要求（2）中，学生用10蓝10红自主创造有规律的图案，进一步创造出“2蓝2红”或其他规律的图案，为后续周期问题的规律研究创造了空间，拓展了间隔排列规律的应用，在应用中实现间隔排列规律的内化与提升。

三、反思——教之道，贵以专

回顾本节课的规律教学，笔者在以下几个方面做了较大的尝试：

（1）丰富探究活动，引导学生从多样的间隔排列素材中“找一找”“说一说”“画一画”，经历多层次的探究活动，发现间隔排列的特征，形成间隔排列规律的表象。

（2）放慢探究脚步，借助四个核心问题驱动学生逐步深入思考、探究，在观察、比较、操作中逐步完善对间隔排列现象中两种物体数量之间关系的认识，把握间隔排列规律的本质，感悟一一对应思想，积累探索规律的活动经验。

（3）巧妙变式，优化作业练习，在应用规律中引导学生从不同的角度思考，幫助学生巩固对数学规律的理解，切切实实把握间隔排列规律的本质，引领学生的数学思维逐步走向深刻。