借助度量结构 促进迁移式学习

高向辉　张艳　刁善玉思佳　刘延革

【摘 要】文章以小学数学图形与几何领域中“长方体和正方体的体积”的学习为例，以北京市小学数学教研团队开发的“单元教学路径”（第二版本）为依据，进行了单元教学的研究与实践。从度量对象、度量单位和度量方法等方面分析度量本质的一致性，结合学生的认知规律，即在角的度量学习中建立起的度量结构的基础上进行迁移，实现发展学生核心素养的目标。

【关键词】核心素养 单元设计 度量结构 自主迁移

新课标在课程实施中提出，要注重教学内容结构化；把握知识间的关联，建立有支撑意义的知识结构，能帮助学生学会用整体的、联系的、发展的眼光看问题，促进迁移式学习，更好发展数学核心素养。

体积是小学阶段最后一次几何度量的学习。在此之前，学生已经学习了长度、面积、角度，探索了共性化的认识路径，积累了学习经验，初步形成了几何度量的认知结构。因此，可以引导学生借助已有的度量学习经验与认知结构，运用迁移学习体积，并在学习过程中进一步丰富完善度量的认知结构，以促进学生形成更广泛的迁移，培养核心素养。下面具体阐述单元整体设计和实施的思考。

一、单元的学习主题及具体观念

（一）聚焦新课标变化，明确度量学习的方向

“长方体和正方体的体积”属于图形与几何领域中“图形的认识与测量”这一主题。新课标将图形认识与测量合并为一个主题，更关注二者之间的联系。对于立体圖形的学习，新课标要求教师引导学生通过对立体图形的测量，从度量的角度认识立体图形的特征，进一步发展空间观念。有关体积的学习内容，新课标提出：要通过实例了解体积的意义，知道体积的度量单位，能进行单位之间的换算，体验不规则物体体积的测量方法，探索并掌握长方体、正方体的体积计算公式，能用这些公式解决简单的实际问题。从中可以看出，新课标是从认识“度量属性”、确定“度量单位”、探索“度量方法”、解决“实际问题”的角度明确了学习内容，提出了具体要求，同时这也是学生认识体积要经历的学习过程。这样的学习过程与长度、面积、角度的学习具有一致性，素养表现是量感和推理意识。

（二）分析教材设计，梳理度量学习的结构

在“长方体和正方体”单元，学生第一次深入研究立体图形，是从二维平面图形到三维立体图形的一次跨越。学生通过展开与折叠、视图与还原、切割与堆积多角度进行二维与三维的转化，了解了长方体、正方体的特征。但如何从量化的角度认识三维空间呢？这就需要引入新的度量属性—体积。

对比人教版、北京版和北师大版小学数学教材，三个版本教材在编排时都引导学生经历“认识度量属性体积—确定体积单位—单位累加度量体积—探索体积与图形要素关系获得公式—选择合适方法解决生活问题”的过程，这样的研究过程与学习长度、面积、角度相同，体现了认知结构的一致性。

北京版和北师大版小学数学教材在编排中更突显沟通长度、面积、体积之间的联系，引导学生借助已有经验和认知结构，运用迁移学习体积度量，丰富对度量内涵的认识，在联系与对比中进一步完善度量的认知结构。这样的学习过程符合学生的认知，也体现了知识的进阶。

综上分析发现，体积与长度、面积、角度都在围绕度量的本质展开教学，它们之间呈现的知识结构和思维方法具有一致性。因此，教学时可以运用类比迁移，引导学生借助已有的学习经验和方法自主探究，使学生体会到度量的认知结构是可以迁移的，能应用到新的度量学习中。在这个过程中，发展量感、推理意识、空间观念，以及解决实际问题能力和创新意识。因此，北京研究团队确定了本单元的学习主题和具体概念。

（三）单元具体概念及学习主题

学习主题：借助结构，促进迁移。

单元具体概念如下：

具体概念一：体积刻画物体所占空间的大小，度量的基本方法是体积单位的累加。通过寻找长方体、正体积与要素之间的关系，获得体积公式。

具体概念二：解决体积问题选取的度量方法和度量单位源于实际生活的需要。

具体概念三：在上述过程中，发展学生量感、推理意识、空间观念，以及解决问题的能力和创新意识。

以上的单元具体概念明确了度量对象、度量过程和素养目标。本单元要在单元具体概念引领下，基于学生已有的认知结构来展开教学。

二、学情分析

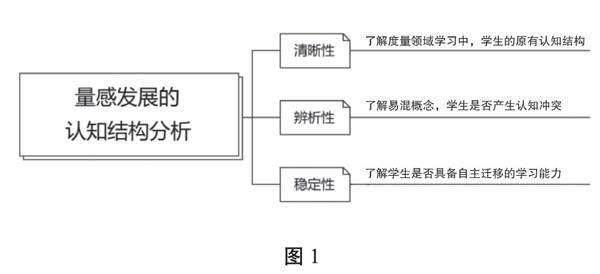
所谓认知结构，就是学生头脑中的知识结构。学生掌握新知识的过程，就是他们逐步完善认知结构的过程。根据教材中度量领域的学习路径分析，得知学生在中、低年级学习长度、面积、角度时，早已进行了结构化的学习。为了突显学生的主体地位，强调知识的理解与迁移，“体积”相关内容的学情分析将分别从认知结构的清晰性、辨析性、稳定性三个方面进行。（如图1）

调研对象：30名五年级学生。

调研目的1：了解度量领域学习中，学生的原有认知结构。

题目1：生活中经常遇到“测量”活动。比如，测量出一个苹果的质量约200克；某学生的身高140厘米；一间屋子的占地面积40平方米；等等。你知道生活中还能测量些什么呢？

通过梳理学生提到的度量属性，大体分为生活中常见的量（质量、温度）、几何的量（长度、角度、面积、体积、容积），还有一些不太熟悉的导出的量（速度、密度、浓度）。其中大部分学生都提到“体积”这个词。

随后，教师以访谈的方式追问学生：“哪些是我们已经能够测量出来的呢？怎样测量？请你举例说一说。”有的学生说：“时间我们可以用钟表来测量，比如一节课40分钟。”有的学生说：“测量温度可以用温度计，比如室温是25摄氏度。”还有的学生说：“人的质量可以用称来测量，我的质量是40千克。”有的学生说：“我用尺子可以测量出一本数学书的厚度是0.5厘米。要求它的面积可以先测出长和宽，然后将长和宽相乘就可以得到面积。”

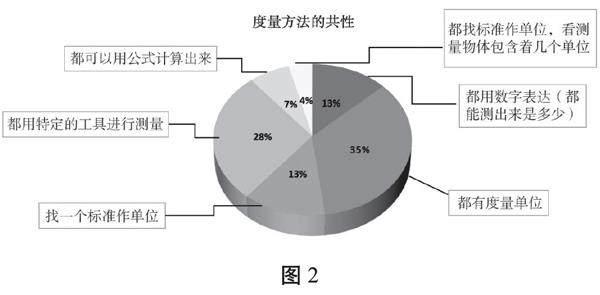
对“这些度量方法之间有没有相同的地方？”这个问题，30名学生，累计收集了46次共同点。这些相同点的占比如图2：

基于这样的数据，教师发现学生提炼的共同点都是通过最直观地观察得到的表象特征，缺乏对度量方法本质和共性之间关联（即为什么会有这些共性）的深层次理解。由此，教师得到调研结果：一方面，学生有着丰富的度量经验，了解常见属性的度量单位和度量工具，会简单应用工具测出相应的数值；另一方面，在学生的认知结构中，度量知识是碎片化的，没有形成清晰的度量性概念的认知结构。因此，在后续的教学中，我们应把“体积”单元的教学内容嵌入更大的“度量”视角，让学生经历类比、推理的思考过程，加深对度量本质的理解，帮助学生构建度量性概念的学习路径。

调研目的2：了解易混概念学生是否产生认知冲突。

题目2：同学们听说过体积吗？什么是物体的体积？

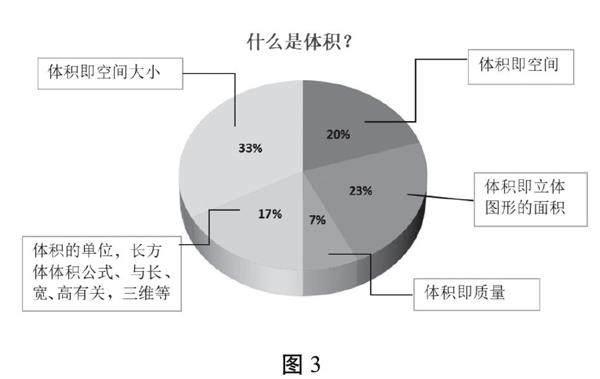
97%的学生听说过“体积”这个概念。对于“什么是物体的体积？”这个问题，调研数据分布如图3：

基于这样的数据分布，教师发现有20%的学生认为体积就是空间，即没有把體积归为是用“数”去表达的量。还有部分学生对体积的理解，受到面积和质量属性的干扰。尤其是受到面积干扰，就像学生在接触一维概念长度和二维概念面积时发生混淆，二维概念和三维概念之间，也发生了混淆。17%的学生没有直接回答什么是体积，但模糊地描述了与体积相关的知识。当然，还有33%的学生说出了体积的含义。面对这样的结果，教师后续设计体积的学习活动时，一是要关注体积概念的本质，因为体积是可测属性，要突显体积是用数量去刻画立体图形的大小的；二是要关注学生受质量和面积属性的干扰，在适当的时候，设计容易产生认知冲突的活动内容，引导学生在辨析中突破认知障碍，从而理解体积的概念。

调研目的3：了解学生是否具备自主迁移的学习能力。

在学生理解体积的概念后，教师想要进一步了解学生在以往度量知识的学习中，是否有一定的知识迁移意识与能力，因此设计如下题目。

题目3：结合长度、面积、角度的学习经验，你们觉得应该从哪些方面来研究体积？对每个方面的内容有哪些猜想？

对于第一小问，学生能够想到可以从体积单位、单位进率、体积计算公式、体积在生活中的应用四个方面进行研究。调研数据统计显示（如图4），大部分学生都能想到2～3个方面，被提到最多的方面就是体积单位和体积计算公式。这表明多数学生能够迁移长度、面积的知识结构，进行体积单位、进率及体积公式和应用等方面学习规划，但是思考不够全面，需要在后续的学习活动中，继续补充完善。同时，从学生的猜想中可以看出，多数学生猜想正确，具有一定的推理意识。

综上分析，学生具备一定知识迁移的能力。在已有的研究中也曾指出，学生进入体积测量学习之前积累了大量的度量经验，无论是度量对象、度量方法，还是解决问题，都可以进行迁移式学习。因此，教师应充分借助学生已有的关于度量学习的认知结构，引导学生自主规划“体积”内容的探究与推理。

三、单元学习目标及结果表现

基于以上分析，我们确定了单元学习目标及结果表现（见表1）。在结果表现中，第1～8条对应知能目标，第9～10条对应理解目标，第11～12条对应迁移目标。

四、学生思考的关键问题及学习任务序列

（一）学生思考的关键问题

由单元具体观念衍生出的关键问题是学习任务的核心，是学生理解、感悟并形成单元具体概念的依据。确立关键问题，可以引导学生开展深度思考和合作交流，是“达到理解意义和自主迁移目标的关键”。基于“体积”单元具体概念，我们设计了本单元需要学生深入思考的三个关键问题。（如图5）

关键问题1指向单元具体概念1。度量刻画的是事物属性的“大小”，其中体会被测事物的属性对于学生是重要的，有时候还是困难的。这个关键问题重点就是思考度量属性，下面对应着两个子问题：子问题1，使学生关注一个度量对象具有不同的度量属性；子问题2，从不同的度量属性中聚焦三维空间的度量，认识体积。关键问题引领学生将体积概念的学习放置度量领域的知识体系中，从更大的度量视角来认识体积，有助于学生建立度量性概念的知识结构。

关键问题2指向单元具体概念1，2，3。这个关键问题旨在借助已有度量认知结构，促进学生运用迁移进行学习。首先迁移在长度、面积、角度学习中获得的知识结构，引导学生自主规划体积的学习内容。然后在规划下展开结构化的学习，联系已有的度量学习经验分别研究体积单位、体积的基本度量方法、图形要素与体积大小的关系，以及如何选择合适的度量方法和单位解决实际问题。在规划与研究的过程中，使学生不断自我完善度量的认知结构，发展学生的量感、推理意识、空间观念，以及解决问题的能力及创新意识。因此，在这个关键问题下对应着四个子问题，分别聚焦如何规划体积学习内容，体积单位的研究，体积公式的猜想验证，解决生活中的体积问题。

关键问题3指向单元具体概念1，3。在完成小学阶段最后一次几何度量学习后，在关键问题3的引领下，通过两个子问题，引导学生沟通不同属性度量之间的联系，丰富度量的认知体系，完善度量的认知结构，并能将结构自主迁移到新属性的度量研究中，形成善于应用结构研究问题的意识，发展学生的量感和推理意识。

在单元具体概念引领下，基于三个关键问题，研究团队设计了学习任务序列。

（二）基于关键问题的学习任务设计框架

本单元共14个学习任务，分6课时进行教学。学习任务的设计体现度量的全过程，注重借助已有的度量认知结构，促进学生在迁移中学习。（如图6）

学习任务1～4突出度量属性，创设有关冰激凌的生活情境，提出多种度量属性，在多种度量属性中聚焦三维空间度量，在度量活动中感受立体图形的三维属性特点，认识到体积的大小是可量化的。学习任务5规划学习内容，借助已有的度量认知结构自主规划，以利于展开结构化的学习。学习任务6～7关注度量单位，迁移长度单位和面积单位的学习经验，根据度量属性先猜想，再统一体积单位的形状、大小与进率，并能灵活选择单位度量，再一次感受单位累加的基本度量方法。学习任务8自学容积和容积单位。学习任务9～10优化度量方法，类比迁移长方形面积公式的学习经验，研究立体图形的要素与体积的关系，获得长方体、正方体体积公式。学习任务11～12解决生活问题，根据实际需要，选择合适的度量方法解决问题。学习任务13～14回顾梳理反思，沟通不同度量属性间的联系，丰富度量体系，完善度量的认知结构，并能迁移到新属性的度量研究中，形成结构化学习的意识。

（三）设计特色说明

1.在多属性测量中激活度量经验

无论是几何领域中的长度、面积、体积等概念，还是生活中常见的量，比如温度、时间、质量等，都具有用“数”去刻画大小的本质。因此，“体积”单元的设计起点并没有从研究体积概念直接入手，而是先将“体积”这一概念嵌入更大的度量知识体系中，体会度量的一致性。教学时创设有关冰激凌的情境，引导学生借助熟悉的“量”，如可以测量冰激凌的质量、冰激凌杯子的表面积、冰激凌的温度等，唤醒度量经验，为后续自主研究体积或其他属性相关内容做好铺垫。

2.在自主规划中迁移度量结构

基于课前的学情调研， 可以发现多数学生能够迁移长度和面积研究的内容，自主规划出研究体积需要从哪些方面入手。课堂中通过学生之间的交流、补充和启发，学生意识到无论长度、面积，还是体积，都需要研究它们各自的单位、进率、计算公式以及灵活解决问题等方面的内容。这样的自主规划，不仅实现了对体积这一数学概念与相关知识的理解，也引导学生进一步关注一维（长度）、二维（面积）、三维（体积）之间的联系，完善几何领域的度量认知。

3.在梳理反思中丰富度量体系

怎样将几何领域的度量结构拓展到更大的一般性度量结构中？和本单元的起始学习任务形成呼应，从一般性度量经验中走进体积的学习，最终还要回到对一般性度量的认识与反思。学生用喜欢的方式整理所有度量学习的发现与再认识。在这些度量内容中，既要梳理长度、角度、面积、体积四次几何度量学习与发现，还要寻找小学阶段其他常见的量之间的联系，从而丰富度量体系，形成结构化思考问题的一般方式，实现真正意义上的自主迁移。

【参考文献】

[1] 吕志新，杨爽，吴晓超.重操作，多角度，促空间观念再提升——“长方体和正方体的认识”单元整体教学设计[J].小学数学教育，2021（21）.

[2] 祁小梅.奥苏贝尔认知结构与迁移理论及教学[J].黑龍江高教研究，2004（5）.

[3] 刘延革，冯林.图形与几何领域的内容结构化分析——以“图形的认识与测量”主题为例[J].小学数学教育，2023（Z1）.

[4] 张丹，于国文.“观念统领”的单元教学：促进学生的理解与迁移[J].课程·教材·教法，2020（5）.

[5] 刘延革，冯林.大观念统领下单元学习任务的开发[J].中小学管理，2021（5）.

[6] 刘延革，冯林.整体视角下有关度量内容的研究与实践[J].小学教学（数学版），2022（1）.

注：本文系北京市教育科学“十三五”规划一般课题“运用大观念发展儿童数学关键能力的实践探索”（课题编号：CDDB2020140）的研究成果之一。