让神奇的“转化”有效渗透
2024-05-15周小苏
周小苏

【摘 要】数学思想方法是数学核心素养的核心,是数学学习的灵魂,也是处理数学问题的指导思想和基本策略。数学新课标明确指出,要使学生理解和掌握基本的数学思想和方法,可见其在数学学习中具有举足轻重的地位。转化是一种重要的解决问题的思想方法,在小学数学中有着广泛的应用。它是把需要解决的问题,通过某种手段,转变成能够解决或比较容易解决的问题,通过对新问题的求解,来解决原问题。在数学学习的过程中,教师要引导学生使用转化的思想解决问题。
【关键词】转化 数学思想方法 小学教学
作为小学数学教师,我们深有感触的是学生学习过的知识很容易被遗忘,而且,在生活和工作中真正能够得到应用的数学知识并不是太多。那么,通过数学学习让学生终身受益的究竟是什么?日本著名数学教育家米山国藏认为,是数学的精神、思维方法、研究方法、推理方法和看问题的着眼点,等等。对此,我们可以理解成尽管许多数学知识被遗忘了,但学生在数学学习中形成的核心素养却会对其生活和工作起着深远的影响。数学思想方法是数学核心素养的核心,它是数学学习的灵魂,也是处理数学问题的指导思想和基本策略。在教学中有意识地渗透数学思想方法,可以使学生自觉地将知识转化为能力,从而形成核心素养。
转化是小学数学教学中一种重要的解决问题的思想方法,它是把需要解决的问题,通过某种手段,将其变成能够解决或比较容易解决的问题,通过对新问题的求解,来解决原问题。曹冲称象、爱迪生测算灯泡的容积等都是运用转化解决实际问题的经典案例。转化在小学数学教学中有大量的应用,在数与代数、图形与几何等领域,转化思想几乎贯穿始终。善于使用转化的思想解决问题,是学生数学思维能力发展的重要特点。下面笔者就如何让转化的思想方法在小学数学教学中进行有效渗透谈一谈自己的几点思考。
一、学贵有困,困而后疏
(一)问题引发冲突
转化实际上就是换个角度想问题。如化繁为简、化新为旧、化难为易、化数为形、化异为同……所有适合用转化思想解决的问题都有一个共同的特点:用常规方法不能或不方便解决。不愤不启,不悱不发。在教学中,需要让学生先有“山重水复疑无路”的困顿,才会有转化之后“柳暗花明又一村”的疏朗,这个过程也是让学生体会“为什么要转化”的绝佳时机。因此,教师要善于利用问题引发冲突,让学生在思而未果、求而不得的状态下试图另辟蹊径,才是转化的正确打开方式。
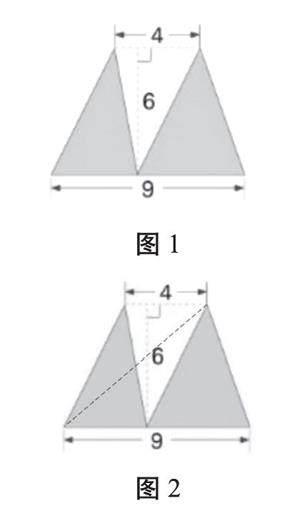
例如,求图1中涂色部分的面积(单位:cm),当教师出示图1后,学生发现如果用“分别求出两个涂色三角形的面积再求和”的常规方法在这里显然不太适合。学生思考后,发现可以转化成“用梯形面积减掉空白三角形面积”来计算。接着,教师可以继续发问:你还有别的方法吗?学生在教师的追问下进入“愤”“悱”的状态,教师适时点拨,让学生发现此题可以通过添加辅助线,将图1转化成图2和图3,将两个分开的涂色三角形转化成面积相等的一个大三角形,问题就被轻松解决了。
由此可见,没有冲突,就不会有豁然开朗、茅塞顿开的感觉。困顿和冲突越强烈,学生对转化的需求也就越强烈,对转化优势的体会才会更充分。
(二)经历增强体验
冲突导致的困顿激发了学生强烈的探究欲望,这时放手让学生通过经历增强体验就显得尤为重要。在数学学习的过程中,无论是概念的形成、性质或定理的得出,还是思想方法的感悟和体会,都离不开学生亲历完整的学习过程。任何一种灌输式的教学都是行不通的。转化作为一种数学思想方法,其本身具有的内隐性更决定了学生需要在学习中不断通过观察、比较、分析、综合、归纳、概括、实验等手段亲身经历数学知识的形成过程,在获得对问题的认识、理解和解决的同时,才能获得对数学思想方法的认识和感悟。
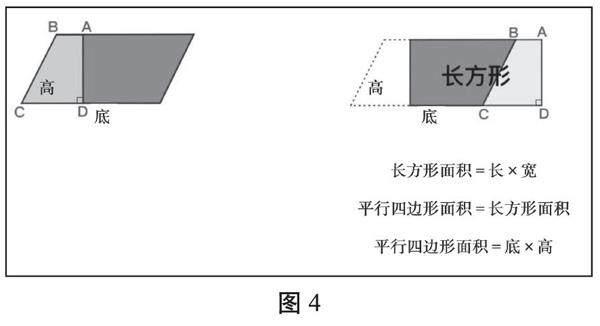
例如,平行四边形面积公式的推导。(见图4)
学生在以上的过程中需要不停地进行观察、比较、分析、归纳、概括……才能在长方形面积计算的基础上“生长”出平行四边形面积计算的公式。如果没有充分的经历,而只是由教师告知一个简单的结论,那学生对转化的思想方法就没有任何体验和感悟。
二、学贵好悟,悟而后明
(一)表达激活思维
数学思想方法是数学思维活动后产生的结果,是对数学知识发生过程的升华,是数学思维的结晶。因此,数学思维活动的质量直接影响着学生数学思想方法的形成。语言是思维的外壳,课堂上通过让学生对学习过程进行个性化的表达,就是在激活其主动思维、深层思维。例如,在平行四边形面积公式推导前,教师可以引导学生就“平行四边形的面积应该怎样计算”展开积极思考和充分表达;在公式推导过程中可以就“怎样将平行四边形转化成长方形”“转化前后的平行四边形和长方形有怎样的关系”“你有什么发现”等问题进行表达;公式推导之后,又可以引导学生完整地说一说“平行四边形面积计算公式是怎样推导出来的”。
在引导学生进行表达的过程中,教师需要激活的是每一个学生的思维。因此,教师要想尽一切办法将表达的重心下移,通过“同桌互说”“小组交流”“集体交流”等多种方式“逼”着学生表达。只有这样,个性化的表达才能展现个性化的思维,学生对思想方法的感悟也在不知不觉中进行。
(二)反思加深体悟
反思,是回头、反过来思考的意思。學生通过对学习过程进行反思,不仅可以加深对所学知识的理解,使学习能力得以提升,还可以使隐含在数学知识中的思想方法更加清晰,实现逐步抽象、概括、凝练的过程。因此,转化的思想方法在小学数学教学中进行有效渗透,要抓住反思这一有效手段,让学生在过程中体会其意义和价值,养成自觉、冷静反思的好习惯,并能紧扣重要环节,思考转化的思想方法如何在问题解决的过程中发挥关键作用,从而对转化的本质意义有更深入、全面的感悟。一般来说,对于转化的思想方法,学生可以在问题解决之后从“为什么需要转化”“具体怎样转化”“转化后怎么样”三大问题入手进行反思。长此以往,学生对需要用转化来解决的问题会有“类”的大致印象,对问题解决时是应该化曲为直、化繁为简、化数为形等都有自己的直接的、经验型的判断,在加深体悟的基础上主动转化的意识也得以加强。
三、学贵梳理,理而后清
(一)回顾感受价值
当高年级的学生在对转化有了深刻的感悟和认识后再回顾整个学习过程,会发现在数的运算、几何图形的面积、体积计算等内容的学习过程中,转化几乎无处不在,它帮助解决了许多原本无从下手的问题。例如,在学习“异分母分数加、减法”时我们将其转化成“同分母分数加、减法”;“小数乘法”转化成了“整数乘法”;“除数是小数的除法”转化成“除数是整数的除法”;“多边形的内角和”转化成“计算多个三角形的内角和的总和”,等等。通过回顾,学生不仅在主动沟通知识间的联系,更是以转化的思想方法为轴,串起了一条知识链,对转化的感悟自然更为深刻。最为重要的是,转化在小学数学中的广泛应用让学生充分感受到其价值所在。
(二)整理明晰特征
学生数学能力和素养的提升,离不开整理和复习这一重要的方式。通过整理和复习,学生头脑中数学认知结构会逐渐完善,也能使隐含在不同数学内容中的同一数学思想方法更加明晰,从而在得到结论的同时,让学生感受到数学思想方法的实用性,提升学生的数学核心素养。因此,在一个单元或一个阶段的学习之后,对知识进行适度的整理与复习是十分必要的。在与转化思想方法相关知识的整理过程中,一是要努力引导学生通过回忆交流在头脑中再现知识的形成过程。二是在整理与复习时要注意强化数学知识之间的内在联系,帮助学生以思维导图的形式进行梳理,并且突出数学知识形成过程中的共性。
例如,总复习“平面图形的面积计算”可以进行整理(如图5):
引导学生梳理这样的思维导图其实就是一个再现知识形成的过程,学生要一边梳理一边将推导过程进行完整的表述,在梳理完毕后加深体会整个平面图形面积计算公式推导过程都是在用转化的思想分析和解决问题。同样,立体图形的体积计算公式推导也是类似的。
四、学貴善用,用而后启
(一)应用养成自觉
数学来源于生活,又应用于生活。学生在数学学习过程中获得的知识、能力都要在实际应用中才能得到巩固和提升,数学思想方法也需要在实际应用中得到提炼。
在教学中,教师要注意引导学生自觉地应用转化的思想方法,将陌生的、未知的、复杂的问题向熟悉的、已知的、简单的问题转化,突出转化的思想方法对解决问题的指导作用。同时,更要引导学生在经历完整解题过程的基础上,充分感悟转化思想对解决问题的指导作用,也体验到解决问题的具体方法向转化思想的转变过程,强化学生的感悟。
例如,修路队修一条路,第一天修了全长的2/7,第二天与第一天所修路程的比是2∶1,还剩500米没修,问这条路全长多少米?
此题中既有分率又有比,应用转化既可以把比转化成分率,按分数实际问题来解答:第二天就是第一天的,也就是全长的×=,这样两天已修全场的,500米对应全长的,全长为500÷=3500(米);也可以把分数转化成比,借助“份数”将问题转化成整数问题来解答。第一天修了两份,第二天与第一天的比是2∶1,说明第二天修了4份,那500米对应全长7份中的1份,全长为500×7=3500(米)。
在实际问题的解决过程中,学生能够明显感知到转化的魅力,化繁为简、化难为易的过程让学生体验到了思维的乐趣。久而久之,自觉应用转化的思想方法解决实际问题的意识也就得以养成。
(二)内化促进提升
数学思想方法的感悟内化是一个漫长的过程,不可能一蹴而就,教师和学生都要有足够的耐心,才能在教学中实现转化思想方法的逐渐内化,学生的核心素养也才能有效提升。一是教师要对转化思想方法的有效渗透做长期的设计和规划,遵循学生思维发展的潜在规律,科学地、循序渐进地进行渗透,促进有效内化;二是教师要成为有心人,善于捕捉隐藏在教学内容中适合用转化解决的问题,有计划、有方法地引导学生充分实践和感知;三是教师要充分利用好反思和整理复习的有效手段促进内化。
综上所述,问题冲突、完整经历、多元表达、深刻反思、及时回顾、系统整理、实践应用、主动内化是实现小学数学教学中转化思想渗透的有效环节和手段,它们就像链条一样串起学生学习的整个过程,为学生数学核心素养的发展提供保障。
【参考文献】
[1]陈祥彬.在小学数学教学中渗透数学思想方法[J].课程·教材·教法,2010(7).
[2]吴正宪.感悟数学思想,积累数学活动经验——从修订后的数学课程标准的两个案例说起[J].基础教育课程,2012(1).
