高斯与平顶光束纳秒脉冲激光物质蒸发烧蚀动力学仿真研究*

尹培琪 许博坪 刘颖华 王屹山 赵卫 汤洁†

1) (中国科学院西安光学精密机械研究所,瞬态光学与光子技术国家重点实验室,西安 710119)

2) (中国科学院大学,北京 100049)

基于建立的纳秒脉冲激光与金属铝相互作用的二维轴对称模型,仿真研究了光束整形对纳秒脉冲激光烧蚀金属铝过程中蒸发烧蚀动力学的影响.结果表明: 等离子体屏蔽对靶材的烧蚀特性具有显著影响,屏蔽效应主要体现在脉冲的中后期.对于3 种激光轮廓,高斯光束的屏蔽效果最强,随着整形后的平顶光束直径的增大,屏蔽效果逐渐减弱.平顶光束与高斯光束作用下,靶材温度的二维空间分布较为不同.高斯光束作用时,靶材中心最先升温,随后温度沿径向和轴向扩散.由于平顶光束的能量分布更加均匀,因此一定径向范围内的靶材同时升温.光束整形对靶材的蒸发烧蚀动力学影响较大.对于高斯光束,靶材中心先烧蚀,随后产生径向烧蚀.由于整形后平顶光束的能量密度降低,因此靶面蒸发时间较高斯光束延后,并且一定径向范围内的靶材同时发生蒸发烧蚀.3 种激光轮廓下,靶材的蒸发烧蚀形貌与光束的强度分布类似,其中高斯光束的烧蚀坑呈中间深两边浅的特点,平顶光束的烧蚀坑较为平坦.

1 引言

激光诱导击穿光谱 (laser induced breakdown spectroscopy,LIBS) 技术具有多元素、微损伤、可远程、原位快速的特点[1-5].目前已广泛应用于诸多领域,包括环境保护[6]、文物鉴定[7]、食品安全[8]、生物检测[9]、工业生产[10]等.多项研究表明光束整形在改善LIBS 信号质量,提高LIBS 信号的灵敏度和准确性方面具有较大潜力[11-14].

Jia等[11]利用衍射光学元件(diffractive optical element,DOE)将高斯光束转换成能量分布均匀的圆形平顶光束测量水泥中的元素含量.研究表明与高斯光束相比,平顶光束产生了更加均匀的烧蚀坑,并获得了更稳定的LIBS 光谱信号和更低的元素检出限(limit of detection,LOD).随后该课题组[12]又探究了激光光束整形对LIBS 在不同基体钢样品中锰元素和铬元素的痕量探测性能的影响.结果表明当使用高斯激光时,由于光束边缘能量低于烧蚀阈值,因此这部分能量仅能加热材料,导致激光能量利用率降低.而光束整形后,由于平顶光束能量分布更加均匀,边缘能量也可用于烧蚀,因此平顶光束的烧蚀更加均匀、稳定,烧蚀坑更平坦、平滑.Hou等[13]通过将激光轮廓从高斯形状整形为平顶形状实现了对激光诱导等离子体演化过程的调制.研究表明采用平顶光束可以显著提高等离子体温度和电子密度,这是由于平顶光束作用下的等离子体屏蔽减弱,样品与激光耦合效率增加.Ji等[14]通过光束整形提高了基于LIBS 检测矿石中铀元素原始信号的能力.研究表明平顶光束的边缘可提供能量用于烧蚀,因此其烧蚀坑直径更大,约为高斯光束的2.5 倍.

上述研究阐释了光束整形后LIBS 信号质量改善的关键因素,分析了光束整形前后靶材烧蚀坑形貌的变化特征,证明了LIBS 信号的质量与激光靶材相互作用过程紧密相关.迄今为止,已有诸多物理模型被提出用以解释纳秒激光的烧蚀过程.通常认为,低激光功率密度下材料主要产生蒸发烧蚀,可通过Hertz-Knudsen 方程估计由蒸发引起的材料烧蚀速度,这也是当前文献采用的通用方法[15-17].而当激光功率密度高于109W/cm2时,除了要考虑蒸发烧蚀外,还要考虑相爆炸机制[18,19].在足够高的激光辐照下,靶材表面温度可达0.9Tc(Tc为材料的热力学临界温度),其中部分靶材可从过热的液体层快速转变为蒸汽和液滴的混合物,随后从材料表面爆炸性喷出,即相爆炸发生[20].

此外,由于激光照射下靶材温度可从室温升高至上千度,这使得材料的吸收系数、电导率和热导率等参数呈现出数量级的变化[21-23],因此温度极大程度改变了材料的光热特性进而影响最终的烧蚀效果.Wu 和Shin[24]基于Drude 模型计算了铝在临界温度附近的吸收系数,研究表明临界温度下铝的吸收系数将降低近2—3 个数量级.Gragossian等[25]评估了从室温到临界温度下材料特性的变化,考虑了蒸发和相爆炸机制,计算了靶材电导率、热导率、密度以及吸收系数的时间和空间分布特性,分析了烧蚀深度随激光强度的变化规律.研究表明随着激光强度的增加,烧蚀深度逐渐增大,但文中数值计算的烧蚀结果高于实验值.Lutey 和Adrian[26]进一步改进了烧蚀模型,不仅考虑了温度对材料特性的影响,还通过假设恒定的等离子体吸收系数来考虑等离子体屏蔽的影响.研究表明,考虑等离子体屏蔽后获得的烧蚀深度与实验值较为匹配.Marla等[27]系统性考虑了温度依赖的材料特性、蒸发和相爆炸机制以及等离子体屏蔽效应,计算了由逆韧致辐射和光电离产生的等离子体屏蔽系数,分析了屏蔽系数和激光强度随时间的变化规律.研究表明,考虑等离子体屏蔽后,靶材中心温度和烧蚀深度均显著降低,这种方法比假设恒定的屏蔽值更接近真实的烧蚀过程.目前有诸多模型也通过该方法考虑等离子体羽流吸收和屏蔽过程[28-30].Zhang等[31]通过引入相变焓考虑了材料相变的影响,结合与温度相关的材料特性、相变、等离子体屏蔽及蒸发和相爆炸等物理特性,建立了纳秒激光烧蚀铝靶的一维模型,并基于该模型分析了靶材中心温度、烧蚀深度等参数随时间的演化规律.

鉴于以上一维模型可探究的物理特性较为局限,随后又有更多维度的模型被开发出来.Ghalamdaran等[32]建立了纳秒激光烧蚀金属靶的二维轴对称模型,但由于激光强度不足以产生相爆炸烧蚀,因此文中仅对靶材的蒸发烧蚀特性进行了讨论.研究表明高斯激光作用下,温度、烧蚀深度和烧蚀速度在靶材中心位置最大,随着径向距离的增大逐渐减小.其中靶材烧蚀速度先增大至最大值,在一段时间内保持稳定后逐渐降低.Wang 和Hahn[33]基于有限元建立了激光辐照铝靶的二维模型,考虑了温度依赖的材料特性、蒸发和相爆炸机制及等离子体屏蔽效应的影响,分析了靶材温度、烧蚀深度以及等离子屏蔽系数的变化规律.研究表明随着激光能量的增大,靶材温度、电子密度及等离子体屏蔽系数逐渐增大.

尽管目前已开发了许多纳秒脉冲的烧蚀模型,但多数研究主要集中于靶材中心的烧蚀特性,包括温度、烧蚀速度和烧蚀深度等,而二维空间下靶材温度和烧蚀坑形貌的动力学过程的相关研究甚少.同时,目前多数文献集中研究高斯光束的烧蚀特性,鲜少关注平顶光束的烧蚀特性.本文结合材料光热特性、相变以及等离子体屏蔽效应,建立了纳秒激光与铝金属作用的二维轴对称模型,基于蒸发和相爆炸两种烧蚀机制探究了靶材的烧蚀动力学.在确认模型有效的条件下,分别研究了高斯光束和平顶光束作用下材料瞬态温度场、蒸发烧蚀深度及蒸发烧蚀坑形貌的动态分布特性.该研究有助于深入理解光束整形前后纳秒脉冲烧蚀的物理机理,为提高LIBS 光谱灵敏度和稳定性的激光参数调控提供可靠的优化策略.

2 数值模型

2.1 热传导

2.1.1 控制方程

纳秒激光与物质相互作用的本质在很大程度上是基于热效应,由于电子热容远远小于晶格热容,首先电子吸收激光能量升温,随后电子通过声子振动将能量耦合到晶格.这个过程发生在皮秒量级,这意味在纳秒脉冲结束前,靶材中的电子温度和晶格温度已达到热平衡,因此可认为纳秒脉冲(脉冲宽度大于0.1 ns)的烧蚀是基于热效应.通常利用傅里叶热扩散定律描述材料内热量的传递过程,材料内部温度场的控制方程[34]为

其中ρ,和k分别代表材料的密度、修正热容和热导率,这些参数都与温度相关;t和T表示时间和温度,r表示径向坐标,z表示轴向坐标,Q(r,z,t)为热源项.根据Beer-Lambert 定律,材料将以体热源的方式吸收激光能量,则热源项可表示为[21,35]

式中R(T)和α(T) 分别为材料的反射率和吸收系数;I0(r,t) 表示到达靶材表面的激光强度,对于高斯脉冲,其时域和空间域均服从如下分布[36]:

其中I0为脉冲激光的峰值强度,r0和τ分别为激光的光束半径(1/e2)和脉冲长度(full width at half maximum,FWHM).

靶材吸收激光能量的过程中会发生相变,当靶材温度超过熔点Tm时,部分材料由固相转向液相并释放相变潜热,在本模型中采用等效热熔法处理相变潜热,即将潜热作为热容的贡献项考虑在传热方程中,修正的热容可定义[37]为

式中,Cp和Lm分别为材料的热容和熔化潜热;fL表示液相体积分数,其表达式[37]为

其中,Ts和Tl为材料的固相和液相线温度.

2.1.2 初始条件和边界条件

热传导(1)式可通过初始条件和边界条件求解:

其中Tatm是环境温度(Tatm=300K),L和H为模型计算域的长度和高度.

等式(7)右边的各项依次代表材料的蒸发能量损失项、热对流和热辐射.其中us为材料的蒸发烧蚀速度,h为热对流系数,ε和σ为材料的表面发射率和Stefan-Boltzmann 常数.

2.2 材料移除

对于高强度脉冲激光,材料移除主要通过蒸发烧蚀和相爆炸实现,当材料温度高于沸点时发生蒸发烧蚀,当材料温度高于0.9Tc(Tc为材料的热力学临界温度)时发生相爆炸烧蚀.本模型使用的激光能量密度较高(20 J/cm2),因此靶材的总烧蚀深度等于蒸发深度和相爆炸深度之和.

2.2.1 蒸发烧蚀

材料吸收激光能量升温并产生熔融、蒸发现象,蒸汽粒子离开靶面时产生烧蚀坑.当入射激光通量相对较低时,材料移除主要由蒸发引起,则由蒸发产生的表面衰退速率(蒸发速率),可通过Hertz-Knudsen 方程[38]描述为

式中β为蒸发系数,可取值0.82;ρ为靶材表面的局部密度;m为靶材粒子的原子质量;kB为玻尔兹曼常数;Ts为靶材表面温度;Psat(T) 表示饱和蒸汽压力,可通过Clausius-Clapeyron 方程[18]计算:

其中Tv为材料的蒸发温度,P0为蒸发温度下的气压,取值为1.01×105Pa,Lv为材料的蒸发潜热.

为了模拟由于材料蒸发产生的靶面移动,采用变形网格技术,使用以下公式表达:

式中,z是边界点的位移矢量,n是单位法向量,Vn是预期的法向网格速度,该值与靶材蒸发速度一致,即Vn=-us.

2.2.2 相爆炸烧蚀

当激光强度足够高时,材料表面温度可超过0.8Tc,此时部分熔融的液体成为超热液体,并且液体层内开始产生均匀的气化核.随着靶材进一步吸收能量,靶面温度逐渐升高至0.9Tc,部分气泡的成核速率将迅速增大,当增大到一定程度时,大量包含液滴和蒸气材料的混合物爆炸性向外喷溅,即相爆炸发生[20].在本模型中,将靶材温度高于0.9Tc的区域视为由于发生相爆炸导致移除,这也是目前多数仿真文献常用的计算方法[25,17,31].

2.3 等离子体屏蔽效应

在激光等离子体产生过程中,由于等离子体的形成时间小于纳秒脉冲的持续时间,因此激光在到达靶面之前,部分能量被等离子体吸收,从而导致激光与靶材表面的耦合效率降低,即产生了等离子体屏蔽效应.等离子体主要通过逆韧致辐射(inverse bremsstrahlung,IB)、光电离(photo-ionization,PI)和米散射(Mie scattering)等机制吸收激光能量.其中,米散射吸收的能量很小,可忽略不计.而铝材料实现光电离需要满足: 激光波长λ≤250 nm,由于本次使用的激光为1064 nm,因此可忽略光电离吸收的激光能量[27],本模型仅考虑由逆韧致辐射吸收产生的等离子体屏蔽现象.

逆韧致辐射吸收主要由电子与原子碰撞吸收和电子与离子碰撞吸收两部分组成,若将其视为一次电离,计算公式如下:

其中me为电子质量(me=9.11×10-31kg),Qe-n为电子与原子的平均碰撞截面(Qe-n=10-36cm5)[39].由方程(11)可知吸收系数取决于等离子体羽流的粒子数密度、温度和激光波长.其中羽流温度可通过Knudsen 层关系求得,具体查看本文补充材料(online)“第S1节Knudsen 层”;粒子数密度可通过Saha-Eggert 方程[29]求得.

通常认为等离子体羽流处于局部热力学平衡状态(local thermal equilibrium,LTE),这意味着中性粒子、电子和离子之间建立了热平衡,假设等离子体中的粒子仅为单次电离,可使用Saha-Eggert方程计算粒子数密度 :

其中xe,x1,x0分别代表电子、离子、中性粒子占总粒子数的比值;IP1(5.98 eV)为铝材料的第一电离势[27];np为总粒子数;Tp为等离子体温度.

已知:

将方程(13)代入方程(12)中求解,可获得电子、一价离子和中性粒子的数密度ne,n1,n0.

对于纳秒激光烧蚀等离子体,IB 过程被认为是等离子体吸收激光能量最重要的机制,基于方程(11)—(13)可求出经等离子体吸收后到达靶面的激光能量:

其中hp为羽流长度,vp为羽流膨胀速度,当考虑等离子体屏蔽时,需将方程(2)中的激光热源由I0(r,t)替换为Ish(r,t) .

2.4 铝材料参数

本文使用的材料为铝金属,由于一方面本研究采用的激光能量密度足够高(20 J/cm2),加热材料时会使其温度达到0.8Tc以上,此时材料发生介电转换,材料的反射率R(T)、吸收系数α(T)、密度ρ(T)和热导率k(T) 等物理参数会发生较大的变化;另一方面文献[27,40,41]表明使用温度依赖的材料参数获得的计算结果更接近实验值,因此模型中使用的材料参数均考虑了温度的影响.材料参数的详细推导过程将在补充材料((online))第S2 节展示.表1 为温度依赖的材料参数,其他热学参数如表2 所列.

表1 温度依赖的铝材料参数[25,28,41,42]Table 1. Temperature dependent aluminum material parameters[25,28,41,42].

表2 铝材料的热学常数[27,41,43,44]Table 2. Thermal constants for aluminum materials(reproduced from Ref.[27,41,43,44]).

2.5 光束整形和激光参数

为了将模拟结果与实验结果进行比较,必须保持数值模型使用的激光参数与实验[45]一致,因此将靶面处的激光半径设为80 μm,激光脉冲的波长和脉宽(FWHM)分别设为1064 nm 和5 ns.若对光束进行整形,则整形后激光强度由高斯分布变成近均匀分布,模型中的光束半径和峰值强度发生了显著改变.图1(a)展示了平顶光束与铝靶作用的示意图.

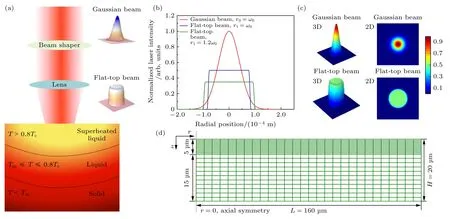
图1 (a)平顶光束与铝靶相互作用示意图;(b)整形前后归一化激光强度;(c)激光光束轮廓;(d)几何模型和网格划分Fig.1.(a) Schematics of the flat-top beam laser interaction with aluminum target;(b) normalized laser intensity before and after beam shaping;(c) laser beam profiles;(d) geometric model and mesh generation.

假设光束整形前后,输入光束与输出光束关于光轴对称(光轴与Z轴重合),且输入光束在垂直光轴截面处的光强分布为g(r),输出光束的光强分布为f(r) .由于实验使用的整形仪器对能量的损耗很小,因此可认为输入光束的功率(能量)与输出光束的功率(能量)是相等的,可得到如下方程:

分别代入高斯光束和平顶光束的强度分布方程,则有

其中r0和I0分别代表高斯光束的光束半径和激光峰值强度,r1和I1分别代表平顶光束的光束半径和激光强度.若令r0=ω0,r1=ω0时,可得到平顶光束的强度为I1=0.5I0;若令r0=ω0,r1=1.2ω0时,平顶光束的强度变为I1=0.35I0.

本模型中使用以上参数的高斯光束和平顶光束(两种尺寸),图1(b),(c)分别为整形前后靶面处激光的二维和三维轮廓图,其中高斯光束受直径限制(1/e2)的光束能量占比为总能量的86.5%,其光强分布特点为中心强边缘弱;平顶光束能量分布较为均匀,随着整形后光束直径的增大,平顶光束的强度逐渐降低.

2.6 计算域、网格尺寸和计算时间

图1(d)为仿真使用的几何模型及网格划分.在模型中,将计算域的长度L和高度H分别设置为160 μm 和20 μm,该尺寸足够大可保证模型边界不受激光的热影响(边界处材料温度始终与环境温度保持一致).为了节省计算资源,对轴向材料采用两种均匀网格尺寸,将靠近激光热源的前5 μm 均匀划分400 个网格(精度为12.5 nm),余下的15 μm粗划分均匀离散为20 个网格(精度为0.75 μm),径向材料均匀划分200 个网格(精度为0.8 μm).完整的网格由84000 个域元素和1440 个边界元素组成,这将为当前的模拟研究提供足够的精度.

本模型基于有限元离散空间域并选择向后差分公式法进行时间步进.模型总研究时间设置为20 ns,确保了所有物理过程均已发生.由于激光峰值时刻附近的靶材温度变化较为剧烈,为了平衡精度和计算成本,使用可变的时间步长,前3 ns 的时间步设置为 0.1 ns,3—7 ns 内时间步为0.02 ns,其余时间步均设置为1 ns.利用直接求解器PARDISO求解方程,其相对容差和绝对容差分别设置为0.01和0.001.

3 计算结果与讨论

3.1 模型验证

为了验证模型的准确性,在不同高斯激光能量密度下,将数值模拟获得的靶材烧蚀深度(考虑等离子体屏蔽)与Porneala 和Willis[45]通过实验测量的烧蚀深度值进行对比.如图2 所示,仿真结果表明在低激光能量密度(F＜ 5 J/cm2)下,靶材仅产生蒸发烧蚀,且烧蚀深度较小.当激光能量密为6 J/cm2时,靶材烧蚀深度瞬间增大,其主要原因是产生了相爆炸烧蚀,并且随着激光能量密度的进一步增大,蒸发和相爆炸机制共同导致了烧蚀深度的增加,这与文献[27,31]的结论一致.

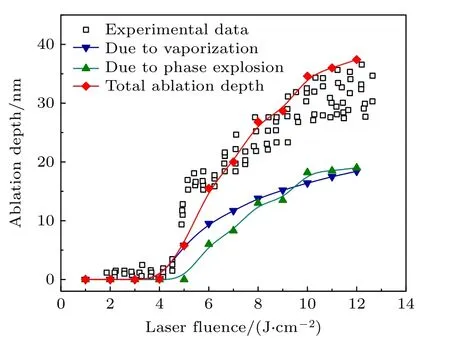
图2 不同激光通量下铝材料烧蚀深度的仿真结果和实验结果[45]对比Fig.2.Comparison of the ablation depth of aluminum with different laser fluences between simulation results and experimental results[45].

另外,从图2 可以看出,仿真获得的铝靶烧蚀深度值和烧蚀深度随激光能量密度的变化规律与实验结果较为一致.并且实验获得的相爆炸阈值处于仿真计算的相爆炸阈值区间.实验值为5.2 J/cm2,仿真获得的阈值区间为5—6 J/cm2.图2 中高激光通量下获得的烧蚀深度值略高于实验结果,这是因为随着激光通量的增大相爆炸逐渐增强,而模型中忽略了因相爆炸损失的热能[27],因此导致数值模拟结果略高.总体来说数值计算结果和实验结果吻合较好,这充分说明基于该模型对激光烧蚀铝靶过程进行模拟是准确可靠的.

3.2 等离子体屏蔽的影响

为方便讨论,设置激光器出射的高斯光束激光通量为20 J/cm2,整形后的平顶光束激光通量分别为10 J/cm2(r1=ω0) 和7 J/cm2(r1=1.2ω0),后文中使用的激光通量均与该数据一致.

3 种轮廓的激光作用下(高斯光束和平顶光束),考虑和未考虑等离子体屏蔽时归一化脉冲激光强度的时间分布如图3 所示.图3 表明,当激光脉冲通过等离子体羽流到达靶面时,脉冲强度显著降低,因此在研究纳秒激光烧蚀过程中等离子体屏蔽效应不可忽视.同时从图3 可以看出,等离子体屏蔽效应主要体现在激光脉冲的中后期,在脉冲峰值强度附近最明显.这是由于在激光脉冲早期,靶面附近主要为蒸汽物质,激光的衰减较弱,因此到达靶面的激光强度未出现明显衰减.而在2.6 ns(红线)、3.6 ns (蓝线)和 4.4 ns (绿线)时,由于蒸汽发生了雪崩式电离形成了初始等离子体,因此等离子体屏蔽效应开始,激光强度开始衰减.随着等离子体变得更加致密以及电离度的增大,屏蔽逐渐增强,在激光强度达到峰值时刻,屏蔽效果最强,随后由于等离子体的扩散和靶面温度的降低,屏蔽程度逐渐减弱.

图3 等离子体屏蔽前后到达靶面的激光脉冲归一化强度的时间分布Fig.3.Temporal profile of the normalized intensity of laser pulse reaching the target surface before and after the plasma shielding.

将等离子体的屏蔽分数定义为考虑等离子体屏蔽时靶面处激光强度的时间积分与未考虑屏蔽时靶面处激光强度时间积分的比值,可获得3 种激光作用时的屏蔽分数.其中高斯光束屏蔽效果最强,等离子体吸收了约22%的能量,随着整形后平顶光束光斑尺寸的增大,等离子体屏蔽效果逐渐减弱.当平顶光束的光斑尺寸为高斯光束的1.2 倍时,屏蔽效果最弱,屏蔽分数约为1%.这是因为高斯光束的峰值功率密度最高,靶材烧蚀量最大,产生的等离子体最致密,因此高斯光束的等离子体吸收系数最大,屏蔽效果最强.

3.3 靶材温度随时间的演化

图4 描述了3 种轮廓的激光作用下,靶材中心处温度随时间的演化规律.从图4 可以看出,高斯光束和平顶光束的温度分布由蒸发烧蚀和相爆炸共同贡献.考虑和未考虑等离子体屏蔽时,靶面温度随时间的演化趋势较为一致.考虑等离子体屏蔽时,靶面温度和高温持续时间(温度高于 0.9Tc的时间)均有明显下降,并且屏蔽导致靶面温度提前降低,因此在研究强纳秒脉冲与物质相互作用时,有必要考虑等离子体屏蔽效应.

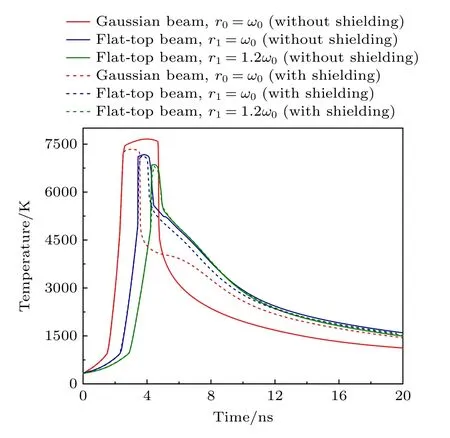
图4 F=20 J/cm2,靶面中心温度随时间的演化Fig.4.Time evolution of target surface center temperature for laser fluence of 20 J/cm2.

以考虑等离子体屏蔽时,靶面中心处温度随时间的演化规律为例进行分析.图4 显示3 种激光轮廓下,靶面温度随时间的发展都经历了3 个阶段,即随着脉冲时间的增加,温度先缓慢上升再快速上升并达到峰值,持续一段时间后,先快速下降后缓慢下降.这是因为刚开始激光作用时,材料吸收激光能量并很快到达熔点.随后,由于熔融后的材料反射率随着靶面温度的升高而减小且材料的热导率随着温度的升高而增大,因此该阶段材料可吸收更多的激光能量,材料快速升温并达到峰值并且在一段时间内,靶材保持高温.随后由于材料蒸发带走了大量的热量再加上等离子体屏蔽效应导致靶面吸收的能量降低,因此靶面温度快速降低.脉冲后期由于等离子体屏蔽效果的减弱,温度缓慢降低.

同时可以看出,当高斯光束作用靶材时,靶面中心处的温度最大,约为7400 K,且高温持续时间最长.由于整形后,到达靶面的激光强度降低,平顶光束烧蚀下靶面中心温度和高温持续时间均较大程度下降,靶材中心处到达最高温度的时刻逐渐向右移动即发生了时间延迟.随着整形后平顶光束光斑尺寸的增大,靶面温度和高温持续时间逐渐下降.

为进一步了解靶材内部的温度变化情况,对一些重要时刻下靶材温度的空间分布数据进行提取,不同时刻下靶材温度的空间分布如图5 所示.

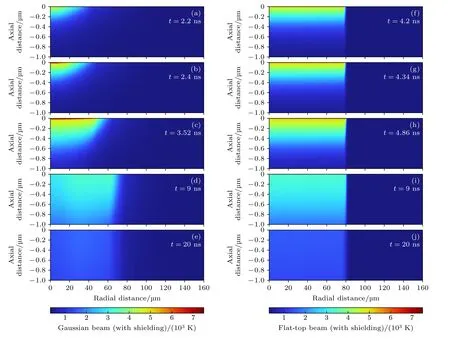
图5 F=20 J/cm2,考虑等离子体屏蔽时,不同时刻的靶材温度分布(a)—(e)高斯光束烧蚀结果;(f)—(j)平顶光束(r1=1.2ω0)烧蚀结果;其中,(a),(f)代表靶材蒸发开始时刻;(b),(g)代表高温开始时刻;(c),(h)代表高温结束时刻;(d),(i)代表靶材蒸发结束时刻;(e),(j)代表靶材仿真结束时刻Fig.5.Temperature distribution of the target for laser fluence of 20 J/cm2 with considering the plasma shielding: (a)-(e) Gaussian beam ablation results;(f)-(j) flat-top beam ablation results;where among them,(a),(f) the initial time of evaporation;(b),(g) the initial time of high temperature;(c),(h) the end time of high temperature;(d),(i) the end time of evaporation;(e),(j) the end time of simulation.

图5(a)—(e)展示了高斯光束烧蚀铝靶的二维温度分布图(考虑等离子体屏蔽),图中表明,当使用高斯光束时,首先靶材中心吸收热能,随后中心温度沿径向和轴向传递至其他区域.当t=2.2 ns时,靶材温度达到沸点,部分材料开始蒸发;当t=2.4 ns 时,由于蒸发散热较少,熔融材料吸收的热量较多,此时材料快速升温;当t=3.52 ns 时,靶材温度达到峰值.随后由于材料快速汽化带走大量的热量,以及热对流和辐射的综合影响,材料温度快速降低,在t=9 ns 时,材料蒸发结束.当t=20 ns 时,远离靶材中心的大部分区域温度降至熔点以下,产生凝固现象.

图5(f)—(j)展示了平顶光束烧蚀铝靶的二维温度分布图(考虑等离子体屏蔽).相比于高斯光束,平顶光束作用下的靶材烧蚀特性有以下3 点不同: 1)由于平顶光束的能量密度降低,导致相同时刻下靶材吸收的能量减少,因此材料蒸发的开始时刻延迟.如图5(f)显示材料在t=4.2 ns 时开始蒸发,比高斯光束延迟了约2 ns.2)由于平顶光束能量分布更加均匀,因此平顶光束作用下,靶面中心和一定径向范围内的材料同时升温.如图5(g)所示,当t=4.34 ns 时,材料内部温度显著上升且温度呈均匀分布.3)仿真结束(t=20 ns)时,高斯光束作用下远离靶材中心的大部分区域凝固,而平顶光束作用下的靶材温度较为均匀,温度降低速度较为缓慢,因此相比于高斯光束,凝固的材料区域较小.

3.4 靶材烧蚀深度随时间的演化

3 种激光轮廓下,考虑和未考虑等离子体屏蔽时,靶材中心处蒸发烧蚀速度和蒸发烧蚀深度随时间的演化如图6 所示.从图6(a)可以看出,材料的蒸发烧蚀速度与靶面温度的演化趋势较为一致,这是因为蒸发烧蚀速度与靶材温度存在正相关关系,即温度的上升直接导致蒸发速度增加.未考虑等离子体屏蔽时,高斯光束的蒸发峰值速度最大,约为18.6 m/s,平顶光束(r1=1.2ω0) 的蒸发峰值速度最低,约为11.7 m/s.考虑等离子体屏蔽后,材料蒸发烧蚀速度在脉冲后期显著降低并且烧蚀速度提前下降.究其原因,是因为脉冲早期材料蒸发较少,不足以产生等离子体屏蔽,烧蚀速度未产生变化;随后蒸发烧蚀量逐渐增加,等离子体屏蔽逐渐增强,从而使得靶面吸收的激光能量减小,因此导致靶面烧蚀速度下降.

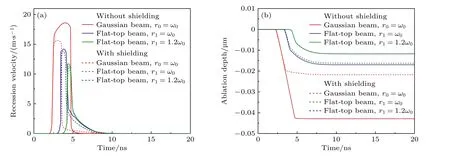
图6 F=20 J/cm2,靶面中心处蒸发烧蚀速度和蒸发烧蚀深度随时间的演化(a)烧蚀速度;(b)烧蚀深度Fig.6.Time evolution of target surface center ablation velocity and ablation depth due to vaporization for laser fluence of 20 J/cm2:(a) Ablation velocity;(b) ablation depth.

从图6(b)可以看出,3 种激光轮廓下,靶材烧蚀深度随时间的演化趋势非常相似.脉冲初期,靶材吸收的能量较低还不足以产生蒸发烧蚀,随后随着吸收能量的增大,靶面温度逐渐升高,蒸发烧蚀深度逐渐增大,脉冲后期由于屏蔽效应的增强及脉冲强度的减弱,靶面温度逐渐下降,烧蚀深度不再增大.对于3 种激光轮廓,高斯光束作用下靶材产生的蒸发烧蚀最早,且其蒸发烧蚀深度最大(42.9 nm);当激光整形为平顶光束时,靶材蒸发烧蚀深度显著降低,随着整形后平顶光束光斑直径的增大,靶材蒸发烧蚀深度逐渐减小.当采用平顶光束(r1=ω0) 时,烧蚀深度为16.9 nm,比高斯光束的烧蚀深度降低了26 nm.当采用平顶光束(r1=1.2ω0)时,烧蚀深度减小为11.8 nm.考虑等离子体屏蔽后,靶材烧蚀深度均显著下降.其中等离子体屏蔽对高斯激光影响最大,其蒸发烧蚀深度减小了近一半(21.2 nm).对平顶光束(r1=ω0) 的影响次之,其蒸发烧蚀深度减小了0.8 nm.对平顶光束(r1=1.2ω0) 的影响最小,其蒸发烧蚀深度减小了0.2 nm.

为了探究光束整形对烧蚀坑形貌的影响,对不同时刻下,靶材烧蚀坑的二维数据进行提取.图7(a)为激光通量为20 J/cm2时,两种激光轮廓下,靶材因蒸发产生的烧蚀坑空间轮廓图.

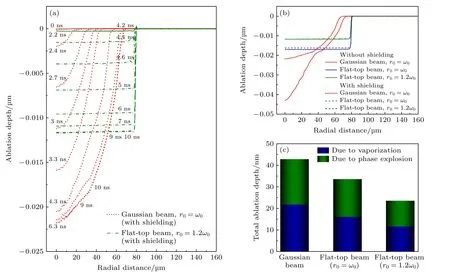
图7 F=20 J/cm2,靶材蒸发烧蚀坑形貌和总烧蚀深度(a)实时蒸发形貌;(b)最终蒸发形貌;(c)总烧蚀深度Fig.7.Target ablation crater morphology due to vaporization and total ablation depth for laser fluence of 20 J/cm2: (a) The realtime morphology due to vaporization;(b) the final morphology due to vaporization;(c) total ablation depth.

从图7(a)可以看出,整形前后激光对靶材的烧蚀行为影响较大.对于高斯光束,由于激光强度具有中心强边缘弱的特点,因此加热靶材时,靶材中心(激光中心)位置先烧蚀,随后产生径向烧蚀.当t=2.2 ns 时,靶材中心处开始烧蚀,随着靶面吸收能量的增大,沿靶材中心的轴向烧蚀深度和径向烧蚀半径逐渐增大.当t=2.4 ns 时,可以观察到明显的烧蚀坑,烧蚀深度为2 nm,烧蚀半径为30 μm.当t=3.3 ns 时,烧蚀深度增至15.9 nm,烧蚀半径增至51 μm,随后烧蚀深度逐渐减缓增大.当t=9 ns 时,烧蚀深度和烧蚀半径达到最大值,烧蚀深度可达21.7 nm,烧蚀半径为71 μm.随后由于靶面温度低于沸点,蒸发烧蚀停止,形成了最终的蒸发烧蚀坑形貌.

与高斯光束相比,平顶光束的烧蚀行为较为不同.由于整形后的平顶光束能量分布更加均匀,因此靶面中心及距中心一定径向范围内的材料同时发生蒸发烧蚀.当t=4.2 ns 时,靶材温度达到沸点开始蒸发,随着靶材吸收的激光能量的增大以及热量的传递,靶材的烧蚀深度同步增大.当t=4.4 ns 时可以观察到明显的烧蚀坑,该烧蚀坑较为平坦,其烧蚀深度为1.5 nm,烧蚀半径为81 μm.随后仅烧蚀深度逐渐增大而烧蚀半径几乎不变.当t=5 ns 时,靶材蒸发烧蚀深度为6.8 nm,比4.4 ns 时增大了5.3 nm,随后烧蚀深度缓慢增大.在9 ns 左右,烧蚀深度达到最大值为11.6 nm,此后烧蚀深度不再增加.

图7(b)展示了3 种激光轮廓下,靶材蒸发烧蚀坑的最终形貌.从图7(b)可以看出,靶材的蒸发烧蚀坑形貌与激光强度的空间分布类似,其中高斯光束在材料中心处烧蚀最深,随着径向距离的增大烧蚀深度逐渐降低.而由于平顶激光的能量分布更加均匀、能量利用率增大,因此烧蚀坑更均匀、平坦,烧蚀坑直径更大.其中高斯光束的径向烧蚀半径为71 μm,轴向烧蚀深度为21.7 nm;而平顶光束(r1=1.2ω0) 径向烧蚀半径略高,约为81 μm,轴向烧蚀深度为11.6 nm.由此可得,与高斯光束相比,平顶光束的径向烧蚀半径增大了近10 μm,轴向烧蚀深度约为其深度的二分之一.Jia等[12]实验观测了高斯光束和平顶光束作用下,不锈钢材料的烧蚀形貌和烧蚀深度.研究表明高斯光束的烧蚀坑具有中间深两边浅的特点,而平顶光束由于更加均匀的能量分布产生的烧蚀坑比高斯光束更平坦、更光滑.该实验结果与图7(b)的仿真结果较为一致.

将蒸发烧蚀深度和相爆炸烧蚀深度相结合,可得到靶材最终的烧蚀深度.图7(c)展示了3 种激光轮廓下,考虑等离子体屏蔽时,靶材的总烧蚀深度.从图7(c)可以看出,3 种轮廓下的相爆炸烧蚀深度普遍高于蒸发的结果,因此可推断相爆炸是高脉冲强度下材料烧蚀率增大的主要原因.对于高斯光束,其蒸发深度和相爆炸深度最大.光束整形后,随着平顶光束光斑直径的增大,蒸发深度和相爆炸深度逐渐减小,因此在高斯光束条件下呈现出最大的总烧蚀深度.

4 结论

本文结合材料光热特性、蒸发和相爆炸烧蚀机制及等离子体屏蔽效应,建立了纳秒脉冲作用金属铝的二维轴对称模型,对比仿真研究了高斯光束和平顶光束纳秒脉冲激光烧蚀金属铝的蒸发烧蚀动力学过程,获得了以下结论.

等离子体屏蔽对靶材的烧蚀特性具有显著影响,即等离子体屏蔽效应导致靶材温度、蒸发烧蚀速度和烧蚀深度大幅度下降.其中,高斯光束的屏蔽效果最强.随着整形光束直径的增大,屏蔽效果逐渐减弱.在等离子体屏蔽过程中,屏蔽效应主要体现在脉冲时间的中后期,脉冲峰值时刻最明显,随后逐渐减弱.

3 种激光轮廓下,靶材中心温度随时间的演化规律较为一致,即随着脉冲时间的延长,靶面温度先缓慢上升再快速上升并达到峰值,持续一段时间后,先快速下降后缓慢下降.其中高斯光束作用下的靶面峰值温度最高,随着整形后平顶光束直径的增大,靶面温度逐渐降低,并且靶面到达峰值温度的时间逐渐延迟.平顶光束与高斯光束作用下,靶材温度的二维空间分布较为不同.高斯光束作用时,靶材中心处最先升温,随后能量沿径向和轴向扩散,靶材内部温度逐渐上升,20 ns 时,远离靶材中心的大部分区域降低至熔点以下,产生凝固.由于平顶光束的能量分布更加均匀,因此,靶面中心及一定径向范围内的材料同时升温.相较于高斯光束,20 ns 时的靶材中心温度较高,凝固的区域较小.

3 种激光轮廓下,靶材中心的蒸发烧蚀速度和烧蚀深度随时间的演化规律较为一致,并且烧蚀速度的演化趋势与靶面中心温度的演化趋势相似.烧蚀深度的演化过程为脉冲初期,靶面吸收的能量较低还不足以产生蒸发烧蚀,因此靶面位置保持不变.随着吸收能量的增大,靶材烧蚀深度快速增大,脉冲后期由于屏蔽效应的增加及脉冲强度的减弱,烧蚀深度缓慢增大.其中,高斯光束的蒸发峰值速度和蒸发烧蚀深度最大,随着整形后平顶光束直径的增加,烧蚀速度和烧蚀深度显著降低.

光束整形对靶材的蒸发烧蚀动力学影响较大.靶材烧蚀坑二维形貌随时间演化的仿真结果表明,对于高斯光束,靶材中心先烧蚀,随后产生径向和轴向烧蚀.烧蚀深度和烧蚀直径随时间持续增加,当靶材温度低于沸点时烧蚀结束,形成了最终的蒸发烧蚀坑,其特点为中间深两边浅.相较于高斯光束,平顶光束作用下的靶材烧蚀行为较为不同.由于整形后平顶光束的能量降低,因此靶面蒸发时间延迟.同时由于整形后平顶光束的能量分布更加均匀,因此一定径向范围内的靶材同时发生蒸发烧蚀,最终形成了平坦的烧蚀坑.