InSb 光栅耦合的太赫兹表面等离激元共振传感方法*

陈钇成 张成龙 张丽超 祁志美3)†

1) (中国科学院空天信息创新研究院,传感技术国家重点实验室,北京 100190)

2) (中国科学院大学电子电气与通信工程学院,北京 100049)

3) (中国科学院大学材料科学与光电技术学院,北京 100049)

仿真设计了一种光栅耦合型太赫兹(THz)表面等离激元(SPP)共振生化传感结构,该结构通过在锑化铟(InSb)基底表面刻蚀亚毫米光栅形成.基于波矢匹配方程的仿真结果表明,当TM 偏振的THz 平行波束以30°入射角照射到光栅区间时,光栅的-1 和+1 级THz 衍射波束能够分别激励传播方向相反的低频SPP 和高频SPP.由于采用商业THz 时域谱装置可以准确测量低频SPP,本文系统地分析了低频SPP 的共振和传感特性对光栅结构参数的依赖关系.仿真结果表明: InSb 光栅耦合的THz-SPP 共振传感芯片的折射率灵敏度随光栅周期的增大而减小;当光栅周期为120 μm、入射角为30°时,折射率灵敏度为1.05 THz/RIU,在此条件下,传感芯片不能对生物分子单分子吸附层作出可探测的响应,究其原因是,低频SPP 的消逝场穿透深度远大于生物分子尺寸,致使两者相互作用不足.为了探测生物分子,仿真分析了多孔薄膜覆盖InSb 光栅的增敏方法.多孔薄膜具有分子富集作用,能够将THz 表面波与生物靶标的相互作用从单分子尺度扩展至整个薄膜厚度,从而提高传感器的生物检测灵敏度.以酪氨酸吸附为例的仿真结果表明,当InSb 光栅表面覆盖厚度为120 μm、孔隙率为0.4 的多孔聚甲基丙烯酸甲酯(PMMA)薄膜后,其吸附灵敏度为0.39 THz/单位体积分数.

1 引言

可见-近红外波段的SPP 共振传感器具有结构简单、制作容易、抗干扰、免标记、高灵敏、高通量、响应快等优点,在国际上获得了广泛研究和应用[1-3].与此相比,THz 波段的SPP 共振传感器鲜有报道,主要原因是常用于产生可见-近红外SPP 共振的金、银等贵金属薄膜的载流子浓度大,其等离子体频率位于远紫外-可见光区间,远大于THz 波段.所以THz 波段的SPP 共振传感器不能利用金、银作为敏感膜,需要使用特殊半导体材料实现[4].取而代之,基于各种THz 超表面的人工表面等离激元(spoof surface plasmon polariton,SSPP)传感器引起了广泛关注.SSPP 的概念于2004 年由Pendry 团队[5]首次提出,他们在金属表面构造了亚波长尺寸的周期性方孔阵列结构,并在这种结构的THz 反射和透射谱中观测到了类似于可见光波段的SPP 共振峰.随后针对THz-SSPP 的研究越来越多[6,7],各类周期性亚波长阵列金属结构层出不穷,SSPP 逐渐成为了THz 领域的研究热点之一[8-10].虽然THz-SSPP 传感器能够通过改变阵列结构调节共振特性,但其往往具有较大的半高峰宽,导致品质因子降低;并且其灵敏度的提高通常会带来结构的复杂性及制备工艺的困难.与THz-SSPP 共振传感器不同,使用特殊半导体作为敏感材料的THz-SPP 共振传感器的传播常数取决于敏感材料本身的介电常数,并且具有与成熟的半导体制造加工相兼容、电磁特性可主动调谐等优点[11].

本文提出一种基于Ⅲ-Ⅴ族窄带化合物半导体材料锑化铟(InSb)的THz-SPP 共振传感器.InSb 兼具可调谐性好和工艺成熟的优点,在THz-SPP 领域备受青睐[12-14].在其表面设计亚波长的光栅结构,通过光栅耦合的方式满足波矢匹配条件,在THz 波段激发SPP.与Kretschmann 棱镜耦合方式或透射测量方式相比,光栅耦合反射式测量不需要控制InSb 衬底的厚度,并且加工与测试方法简单,易于集成;与Otto 棱镜耦合的方式相比,其不需严格控制棱镜与InSb 之间的间隙厚度,操作简单.考虑到与TDS 结合进行实验测量水溶液时,水在THz 波段强吸收的影响,本文进一步提出使用疏水的多孔材料覆盖在光栅表面,仿真结果与未覆盖多孔层相比,不仅能够克服传统的压片样品测试方法无法实现微量检测、滴涂烘干检测中由于咖啡环效应导致待测物分布不均匀等缺点,同时利用多孔材料超大比表面积的特性和富集生化分子的能力,显著提高了传感器的吸附灵敏度.

2 THz-SPR 传感结构中的光栅结构设计及传感机理研究

2.1 结构设计及原理

首先利用Drude 模型对InSb 材料的介电常数进行计算,并根据光栅耦合实现波矢匹配原理,对光栅耦合型InSb 基THz-SPP 共振生化传感芯片进行结构设计.

2.1.1 Drude 模型

现有的研究表明,使用Drude 模型计算InSb介电常数的结果与实验结果基本吻合[15].因此本文使用Drude 模型计算InSb 的介电常数[13]:

式中,ε∞是InSb 的高频介电常数[16],ωp是InSb的等离子体角频率,γc是InSb 的弛豫频率.ωp和γc可表示为[17]

(2)式中,n为InSb 的载流子浓度,e=1.602×10-19C 为载流子的电荷量,m为载流子的有效质量,ε0=8.8542×10-12F/m 为绝对介电常数;(3)式中,u是InSb 的电子迁移率.

依据(1)—(3)式所求得的InSb 介电常数如图1 所示.

图1 使用Drude 模型计算的InSb 介电常数Fig.1.InSb dielectric constant calculated with the Drude model.

2.1.2 色散曲线

光栅耦合激发SPP 原理如图2 所示,图中nd是介质折射率,εm是InSb 的介电常数,k和kspp分别为空气中的光波矢和光栅耦合激发的表面等离子体波矢,θ是光波的入射角,Λ为光栅周期,h0为光栅高度,d为光栅宽度.

图2 光栅耦合原理示意图Fig.2.Schematic diagram of grating coupling principle.

如(4)式所示,由于等式左边第一项始终小于等式右边项,所以正常情况下无法直接激发SPP.而光栅耦合的原理,是将与表面等离子体波矢同向的某一衍射波束与表面等离子体波(SPW)耦合,实现入射THz 平行波束与SPW 的波矢匹配.在现有的研究中,一般选择“±1 ”衍射级进行耦合,因为衍射级数越小,光的能量越强;并且越小的衍射级将带来越大的折射率灵敏度.

式中,k0为真空中光波矢.依据使用Drude 模型计算得到的介电常数和光栅耦合波矢匹配原理,可以得到InSb 光栅耦合激励THz-SPP 的色散曲线,图3 以掺杂型InSb 的+1 和-1 衍射级为例,光栅周期为120 μm.

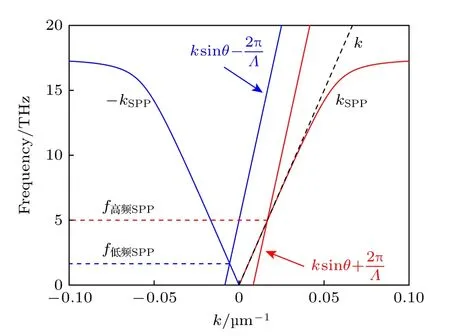
图3 掺杂型InSb 色散曲线Fig.3.Dispersion curve of doped InSb.

通常,SPP 的激发需要(4)式满足εm≫nd2的条件,因此可根据公式f=c/λ将(4)式简化为

1．2．2 声阻抗测试 声阻抗通过对鼓膜外侧声能传导过程变化的测量，了解中耳功能状态。鼓室导抗图主要分为三型［3］。A型：即钟型，特点是最大声顺应值是在正常的大气压（ommH2Oopa）它表明鼓膜正常，咽鼓管功能良好，见于正常耳。B型：平坦无峰，见于鼓室积液，耵聍堵塞。C型：鼓室图形态正常，但偏负压超过－150dapa，幅度在正常范围，见于中耳负压、咽鼓管功能障碍。

式中,fR代表光栅的共振频率.根据(5)式计算可以得到,当THz 平行波束以30°入射角照射到光栅区间时,±1 衍射级分别激励的高频SPP 和低频SPP 的共振频率随光栅周期的变化规律,如图4所示,当光栅周期Λ一定时,+1 衍射波束耦合激励的SPP 共振频率高于-1 衍射波束所激励的SPP,以下分别称为高频SPP 和低频SPP.而市面上常见的THz-TDS 系统在高频波段通常存在严重的信号失真现象,因此本文选用入射光的-1 衍射波束进行波矢匹配,激发低频SPP.值得指出的是,改变THz 波入射到光栅区间的入射角,会对THz-SPP 共振传感结构的工作频率产生影响,可以在考虑待测物折射率和所使用THz 仪器的基础上灵活选择入射角.

图4 低频SPP 与高频SPP 的共振频率随光栅周期的变化Fig.4.Resonance frequency variation curves of low-frequency SPP and high-frequency SPP with grating period.

2.2 仿真分析

本文所有的仿真工作利用有限元分析仿真软件完成,使用Floquet 周期性边界条件和物理场控制划分网格的方法对光栅的结构参数进行计算.为简化仿真模型,仅构建一个周期单元结构,仿真模拟自由空间频率为0—2 THz 频段的THz 波与光栅的相互作用,入射角度设置为30°.由图4 得知,当光栅周期为125 μm 时,共振频率为1.6 THz,表现在反射光谱中即吸收峰的位置处于1.6 THz 处.将参数代入仿真软件中进行验证,设置光栅高度10 μm,光栅占空比v(v=d/Λ)为0.4,得到反射光谱如图5 所示.图5 中纵坐标反射率定义为0 级衍射光强度与入射光强度之比.值得指出的是: 这种反射率定义会影响SPP 共振频谱的对称性,但不影响SPP 共振频率的准确确定.从图5 光谱图可以明显地看出,在光谱1.6 THz 处存在明显的反射率下降,即SPR 吸收峰,与由Matlab 软件计算得到的结果相吻合,此时的反射率为0.42094.

2.2.1 光栅周期的影响

由(5)式可知,利用-1 级衍射波束耦合激励低频SPP,在THz 平行波束入射角θ和介质折射率nd不变时,传感结构的共振频率只与光栅周期相关,共振频率随着光栅周期的增大而减小;因此该部分仿真工作中设置光栅高度为10 μm,光栅占空比为0.4,光栅周期依次设置为125,133,143,154,167 μm,得到五个不同周期光栅的反射光谱如图5所示.可以看出,随着光栅周期的变大,共振频率逐渐向低频方向移动,由125 μm 时的1.6 THz 红移至166.67 μm 的1.2 THz,符合Matlab 软件依据(5)式所计算得到的结果.

2.2.2 折射率灵敏度计算

SPP 共振传感器的敏感机理是折射率改变导致的共振频率变化,而光栅共振频率仅与光栅周期相关.因此本小节设置光栅高度为10 μm,光栅占空比为0.4,光栅周期设置为120—150 μm,步长为5 μm;介质层折射率nd变化范围为1—1.1,步长为0.02;对光栅周期对传感器折射率灵敏度的影响进行仿真分析.图6(a)为120 μm 周期光栅的共振频率随介质折射率变化的仿真结果,共振频率随着介质折射率的增大而不断红移.通过线性拟合结果可知,折射率灵敏度为1.05 THz/RIU;图6(b)为不同周期光栅的折射率灵敏度计算结果,依据结果可知,光栅周期越小灵敏度越高,而由图5 可知,小的光栅周期对应于大的起始共振频率,因此,对于THz-SPP 传感器件,其起始共振频率越大,灵敏度越高.

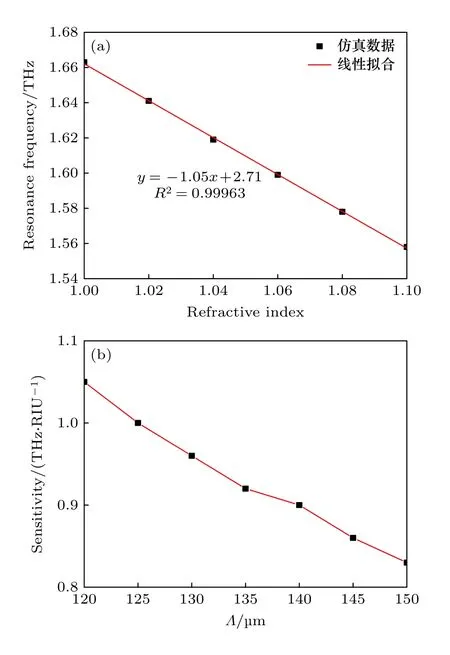
图6 (a) 光栅周期为120 μm 时共振频率随介质折射率的变化,及线性拟合得到的折射率灵敏度;(b) 折射率灵敏度随光栅周期的变化Fig.6.6.(a) Resonance frequency variation curve with medium refractive index when the grating period is 120 μm,and the refractive index sensitivity obtained by linear fitting;(b) variation curve of refractive index sensitivity with grating period.

通过上述对光栅参数及灵敏度的仿真分析,并且考虑到传感结构实现过程中光栅刻蚀的复杂程度,本文后续工作中均设定光栅周期为120 μm,光栅高度为10 μm,光栅占空比为0.4.

2.2.3 吸附灵敏度计算

THz 在生化传感检测领域通常采用离位测试的方法,而离位测试中的吸附测试相比于样品压片、涂覆、沉积等方法[18-21],能够有效并准确地表征传感芯片的性能,本小节将对所设计传感结构的吸附灵敏度进行仿真计算.生化分子的直径普遍处于纳米量级,因此设定光栅表面吸附的生化物质单分子层厚度为10 nm;吸附质选取酪氨酸进行研究,其在THz 波段的折射率为1.507[22].图7 为InSb光栅表面吸附10 nm 酪氨酸与未吸附时的反射光谱,两者几乎重叠,由此可见其吸附灵敏度微乎其微,究其原因是THz 波段SPP 表面波的消逝场穿透深度远大于吸附的生化物质单分子层厚度,致使绝大部分场增强区域未被利用,两者相互作用不足.

图7 光栅表面吸附10 nm 酪氨酸与未吸附时的THz 反射谱Fig.7.THz reflection spectrum of 10 nm tyrosine adsorbed on grating surface and without adsorption.

3 多孔PMMA 覆盖的InSb 光栅结构传感特性研究

水在THz 波段的强吸收性使得THz 在对人体检查或成像方面表现出优异性.THz 波无法穿透水层,对人体进行检查或成像时不能穿透人体的皮肤,对人体的影响只是停留在皮肤表层,而不像微波可以穿透人体,所以更加安全.但同时,水对THz 波的强吸收性也为THz 在检测、传感水溶液领域的应用带来了巨大的阻碍.目前常见的解决办法是采用微流道技术,通过将水溶液厚度控制到微米量级,实现对水溶液的探测.但已有的研究表明,50 μm 厚的水膜就会对THz 波能量带来大约50%的透射吸收[23],因此这种方法的信噪比一般较低,无法实现精确检测;同时微流道工艺较为复杂,制作成本高.因此,针对上述的困难和提高吸附灵敏度的需求,提出使用多孔PMMA 材料覆盖光栅结构,制备流程如图8 所示.多孔PMMA 作为介孔层吸附水溶液中的待测物质,同时,PMMA 的疏水性会使水无法进入其孔隙中,能够排除水对THz波强吸收的影响.

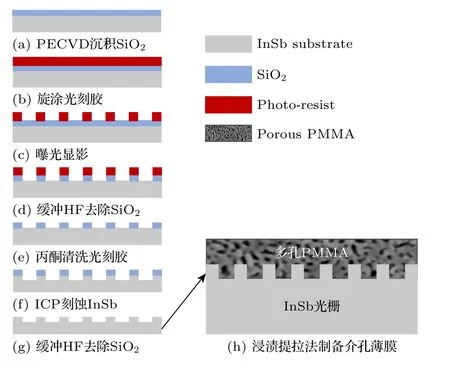
图8 InSb 光栅表面覆盖多孔PMMA 薄膜制备流程示意图Fig.8.Schematic diagram of the preparation process of InSb grating covered with porous PMMA film.

由于多孔结构的存在,多孔PMMA 的等效折射率可以通过改变孔隙率和填充物来调控,根据Bruggenman 公式可以得到其等效折射率n的表达式:

式中,η1,η2,η3分别是PMMA、孔内介质和孔内吸附质所占的体积分数;n1,n2,n3分别对应着三者的折射率,且满足η1+η2+η3=1 .当孔内没有吸附待测分子时,η3=0,此时孔隙率P=η2=1-η1.由此可以得到多孔PMMA 的等效折射率n随孔隙率P的变化曲线,如图9 所示.

图9 多孔PMMA 等效折射率n 随孔隙率P 的变化Fig.9.Variation curve of equivalent refractive index n of porous PMMA with porosity P.

3.1 多孔PMMA 孔隙率及厚度对折射率灵敏度的影响

3.1.1 多孔PMMA 孔隙率对折射率灵敏度的影响

光栅表面覆盖的多孔PMMA 薄膜,其孔隙率决定等效折射率,进而影响传感器的折射率灵敏度.仿真分析覆盖厚度h=25 μm 的多孔PMMA薄膜,传感器在多孔PMMA 不同孔隙率的条件下对介质层折射率nd变化的响应.设置孔隙率P为0—1,步长为0.1;设置nd范围1—1.1,步长为0.01;光栅周期为120 μm,占空比为0.4,仿真结果如图10(a)所示.随着多孔PMMA 孔隙率的增大(即多孔层等效折射率的减小),传感器的折射率灵敏度逐渐增大.然而,与第2 节裸光栅传感结构相比,多孔PMMA 层覆盖的光栅传感结构的折射率灵敏度有不同程度的降低,孔隙率越大,降低程度越小,当多孔PMMA 层的厚度为25 μm,孔隙率为1 时,折射率灵敏度从裸光栅结构的1.05 THz/RIU 降低至0.98 THz/RIU.

图10 在厚度h=25 μm 情况下的仿真结果(a) 折射率灵敏度随多孔PMMA 孔隙率P 的变化;(b) 介质层平均电场模随多孔PMMA 孔隙率P 的变化;(c) 不同孔隙率下的场分布示意图;(d) 不同孔隙率下介质层与多孔PMMA 层界面处的电场强度;其中图(b),(c),(d)均为介质层折射率 nd=1 的结果Fig.10.Simulation results in the case of h=25 μm: (a) Variation curve of refractive index sensitivity with porosity P of porous PMMA;(b) variation curve of average electric field mode of dielectric layer with porosity P of porous PMMA;(c) schematic diagram of field distribution under different porosity;(d) the electric field intensity curve at the interface between the dielectric layer and the porous PMMA layer under different porosity.Note: panels (b),(c),(d) are the results under the condition that the refractive index of the dielectric layer nd=1 .

对场强分布的仿真及计算结果很好地印证了折射率灵敏度的变化规律.图10(b)所示为不同孔隙率时,覆盖多孔PMMA 层后介质层的平均电场模强度,介质层平均电场强度随着孔隙率的增大而增大,与折射率灵敏度随孔隙率变化的响应一致.图10(c)所示为不同孔隙率时的场分布,可以看出,孔隙率越大,介质层的场强越强.这是由于多孔层孔隙率越大,等效折射率越小,其对电磁场的束缚作用越弱,辐射到介质层的场越强.图10(d)为不同孔隙率时,介质层与多孔PMMA 层界面处的电场强度曲线.

3.1.2 多孔PMMA 厚度对折射率灵敏度的影响

本小节设置多孔PMMA 孔隙率P=0.4,仿真分析传感器在多孔PMMA 不同厚度的条件下对介质层折射率nd变化的响应.设置多孔PMMA层厚度为15—40 μm,步长为5 μm,仿真结果如图11 所示.孔隙率为0.4 的多孔PMMA 的折射率灵敏度随着厚度的增大而不断降低,由15 μm 时的0.96 THz/RIU 减小至40 μm 的0.51 THz/RIU.对场强分布的仿真及计算结果很好地印证了折射率灵敏度对多孔层厚度的响应.图11(b)所示为不同厚度时,覆盖多孔PMMA 层后介质层的平均电场强度,平均电场强度随着厚度的增大而减小,由15 μm 时的10106 W/m 减小至40 μm 时的4817 W/m,这与折射率灵敏度随高度的变化规律一致.图11(c)所示为不同厚度时的场分布,可以看出,场强主要集中在介质层与多孔层界面处,并且场强随着多孔层厚度的增加不断减弱.这是由于当孔隙率一定即多孔层折射率一定时,多孔层对电磁场的束缚作用相同,多孔层厚度的增大意味着介质层逐渐远离光栅,辐射的场强也随之减弱.图11(d)为不同厚度时,介质层与多孔PMMA 层界面处的电场强度曲线,同样符合折射率灵敏度随多孔层厚度的增大而减小的规律,并且可以看出,场强主要集中在光栅脊的两个尖端.

图11 在孔隙率P=0.4 情况下的仿真结果(a) 折射率灵敏度随多孔PMMA 厚度h 的变化;(b) 介质层平均电场模随多孔PMMA厚度h 的变化;(c) 不同厚度下的场分布示意图;(d) 不同厚度下介质层与多孔PMMA 层界面处的电场强度曲线;其中图(b),(c),(d)均为介质层折射率 nd=1 的结果Fig.11.Simulation results in the case of P=0.4: (a) Variation curve of refractive index sensitivity with porous PMMA thickness h;(b) variation curve of average electric field mode of dielectric layer with thickness h of porous PMMA;(c) schematic diagram of field distribution under different thickness;(d) the electric field intensity curves at the interface between the dielectric layer and the porous PMMA layer under different thickness.Note: panels (b),(c),(d) are the results of the refractive index of the dielectric layer nd=1.

3.2 多孔PMMA 孔隙率及厚度对吸附灵敏度的影响

3.2.1 多孔PMMA 孔隙率对吸附灵敏度的影响

使用多孔PMMA 来实现低浓度待测物的探测,其优势在于,利用多孔材料超大的比表面积与富集待测生化分子的能力,将SPP 消逝波与待测物质相互作用的区域由单分子尺度扩大至整个多孔层厚度.依此实现提高灵敏度的原理是孔内吸附待测物质而导致的多孔PMMA 等效折射率的改变.因此,吸附相同体积分数的酪氨酸,多孔PMMA 等效折射率变化量越大意味着灵敏度越高.所以本节使用不同孔隙率的PMMA 模型,对吸附体积分数η3=0,0.05,0.10,0.15,0.20 的酪氨酸进行等效折射率仿真计算,得到结果如图12(a)所示.当孔隙率P固定时,随着吸附酪氨酸体积分数η3的增大,等效折射率n不断增大.图12(b)为吸附酪氨酸体积分数由η3由0 变为0.2 时,不同孔隙率多孔PMMA 等效折射率的变化量Δn,结果显示,当孔隙率为0.4 时,Δn(η3=0→0.2) 最大为0.10488.

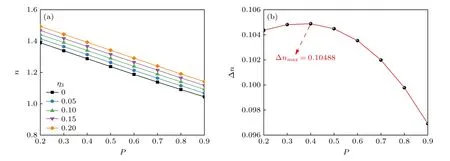
图12 (a) 不同孔隙率下多孔PMMA 吸附酪氨酸体积分数 η3=0,0.05,0.10,0.15,0.20 时的等效折射率n;(b) η3 由0 变为0.2 时,不同孔隙率多孔PMMA 的等效折射率变化量ΔnFig.12.(a) Equivalent refractive index n when the volume fraction of tyrosine adsorbed by porous PMMA η3 is 0,0.05,0.10,0.15 and 0.20 under different porosity;(b) the change of equivalent refractive indexΔn of porous PMMA with different porosity when η3 changing from 0 to 0.2.

3.2.2 多孔PMMA 厚度对吸附灵敏度的影响

由3.1 节分析多孔PMMA 孔隙率对吸附灵敏度影响的结果,本节拟定分析多孔PMMA 层厚度对吸附灵敏度的影响时,设置多孔PMMA 的孔隙率P=0.4,其吸附酪氨酸体积分数η3=0,0.05,0.10,0.15,0.20 时的等效折射率分别为n=1.2875,1.3137,1.3399,1.3661,1.3924.设置厚度为20—240 μm,步长20 μm,仿真结果如图13 所示.由图13(a)可知,覆盖40 μm 厚的多孔PMMA 时,随着吸附酪氨酸体积分数的增大,多孔PMMA 的等效折射率n不断增大,共振频率向低频移动,此时光栅的反射光谱仅有一个共振吸收峰,表明此时40 μm 的多孔PMMA 厚度只有一个共振模式,以下用mode0 表示.该厚度下共振频率fR随吸附酪氨酸体积分数η3的变化如图13(b)所示,以吸附单位体积分数酪氨酸引起的共振峰移表示其吸附灵敏度,线性拟合结果为0.245 THz/单位体积分数;而随着厚度增加到120 μm 时,mode0 相应的吸附灵敏度增大到0.39 THz/单位体积分数,并且反射谱出现第二种共振模式,以下用mode1 表示,对应的吸附灵敏度为0.21 THz/单位体积分数,如图13(c)所示.多孔PMMA 的厚度h继续增大,mode0 的吸附灵敏度呈现饱和态势,维持在0.39 THz/单位体积分数左右;mode1 的吸附灵敏度增大至0.4 THz/单位体积分数.将不同厚度的孔隙率P=0.4 的多孔PMMA 的吸附灵敏度如图13(d)所示.

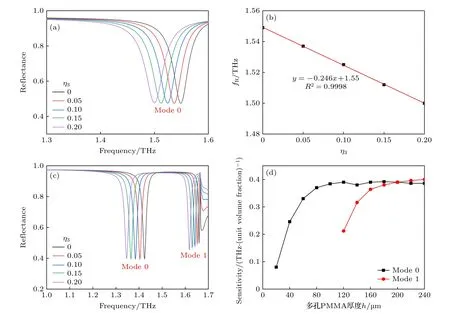
图13 在孔隙率P=0.4 条件下的仿真结果(a) 覆盖厚度为40 μm 的多孔PMMA,传感器吸附不同体积分数酪氨酸的反射光谱;(b) 覆盖厚度为40 μm 的多孔PMMA,传感器吸附不同体积分数酪氨酸的共振频率变化曲线,及线性拟合得到的吸附灵敏度;(c) 覆盖厚度为120 μm 的多孔PMMA,传感器吸附不同体积分数酪氨酸的反射光谱;(d) 覆盖20—240 μm 厚度的多孔PMMA,传感器吸附灵敏度变化曲线Fig.13.Simulation results in the case of porosity P=0.4: (a) The reflection spectra of the sensor after adsorption of tyrosine with different volume fractions when the thickness of the covered porous PMMA is 40 μm;(b) the resonance frequency curve of the sensor after adsorption of tyrosine with different volume fractions and the adsorption sensitivity obtained by linear fitting when the thickness of the covered porous PMMA is 40 μm;(c) the reflection spectra of the sensor after adsorption of tyrosine with different volume fractions when the thickness of the covered porous PMMA is 40 μm;(d) variation curves of sensor adsorption sensitivity when the thickness of covered porous PMMA is 20-240 μm.

4 总结

本文仿真研究了一种基于InSb 半导体材料的光栅耦合型太赫兹SPP 共振生化传感结构.依据光栅耦合原理,TM 偏振的THz 平行波束以30°角照射到光栅表面时,其±1 级THz 衍射波束能够分别激励传播方向相反的低频SPP 和高频SPP.借助有限元仿真软件,对低频SPP 的共振特性和传感特性进行了仿真分析.结果表明,随着光栅周期的增大,低频SPP 共振频率逐渐增大,其折射率灵敏度不断降低,而且在光栅表面吸附的酪氨酸单分子层不能引起低频SPP 共振频率的变化,这是由于THz 波段SPP 的消逝场穿透深度一般在百微米级,远大于酪氨酸单分子吸附层的厚度,致使两者的相互作用不足.

为了提高传感芯片的生化探测能力,本文进一步提出了多孔PMMA 薄膜覆盖InSb 光栅的增敏方法,并仿真分析了增敏效果.结果表明,当多孔PMMA 薄膜厚度≥20 μm 时,该薄膜能够作为THz 漏模光波导,并且在孔隙率为0.4 时,薄膜等效折射率对酪氨酸的吸附最为敏感.在该孔隙率下,覆盖120 μm 厚的多孔PMMA 薄膜,传感芯片的吸附灵敏度达到0.39 THz/单位体积分数.这意味着按常规THz-TDS 系统的频谱分辨率,很容易被观测到不足百分之一体积分数的酪氨酸引起的共振频移,证明了覆盖多孔PMMA 薄膜提高传感芯片生化探测能力的可行性.超大的比表面积赋予了多孔薄膜优越的分子富集能力,能够将THz-SPP波与生化分子相互作用的区域扩展至整个薄膜层,从而大幅提高传感结构检测生化分子的灵敏度,将多孔薄膜引入到THz 生化检测领域拥有巨大的应用潜力.