一类二阶哈密顿系统解的多重性
2024-05-13潘俊蓬陈莹莹
潘俊蓬,陈莹莹
(华北水利水电大学 数学与统计学院,河南 郑州 450046)
0 引言
1996年,艾克兰(Ekeland)等[1]研究了以下问题

x(0)=x0;x(1)=x1.


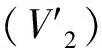
1999年,布尔(Bolle)等[2-3]引入连续路径将结果推广至p>2的情形.本文将继续研究p>2时Bolza边值问题无穷多解的存在性.考虑算子方程Ax-▽Φ(x+y0)=0,其中φ满足
(φ1)存在μ>2,c1≥0,使得对任意y∈Z
μΦ(y)≤Φ′(y)y+c1.
(φ2)存在c2>0,c3>0,μ>2,使得对任意y∈Z
通过极小极大方法,在假设临界值序列以超二次速度逼近无穷的条件下证得其有无穷多解,之后将结果应用于一个非齐次二阶哈密顿系统,证得其存在无穷多解.
1 算子方程
考虑算子方程
Ax-▽Φ(x+y0)=0.
(1.1)
其中A是X中的一个无界自伴算子,且X=L2([0,1];Rn),谱集σ(A)=σd(A)是下方有界的.令Z=D(|A|1/2),带有范数
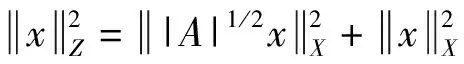
Φ∈C1(Z,R),▽Φ:Z→X是弱连续的,即对任意序列{xk}∈Z,使得xk在Z中弱收敛于x,且在X中有
▽Φ(xk)→▽Φ(x0).
对任意x,y∈Z有
Φ′(x)y=(▽Φ(x),y)X.
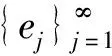
Aej=λjej,j∈N*.
由定义可知

定义

取λ0=1+2|λ1|,则
是Z中的一个等价范数.
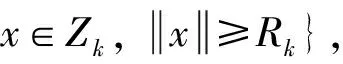
(1.2)
设E是实的希尔伯特空间,I:[0,1]×E→R是一个C2泛函,用(·,·)表示E中的内积,‖·‖表示相应的范数,I′表示I关于x的Fréchet导数.考虑以下假设:
(H1)I满足Palais-Smale条件.即对于(θk,xk)∈[0,1]×E,使得当k→∞时‖I′(θk,xk)‖→0,且I(θk,xk)是有界的,则(θk,xk)在[0,1]×E中有一个收敛子序列.
(H2)对任意的b>0,存在常数c1(b)>0使得|I(θ,x)|≤b且
(H3)存在常数c>0,对I(θ,x)的一个临界点x,有
(H4)I(0,·)是偶的.
对E的任意有限维子空间W,当y∈W和‖y‖→∞时,有
设E1⊂E2⊂…⊂Ek⊂…是E的子空间,且Ek的维数等于k,并且有

引理1设I(θ,x)满足(H1)(H2)(H3) (H4),则对任意的k
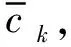
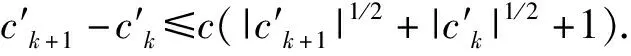
证明详细证明过程见文献[3]的定理2.2.
定理1设算子方程满足(φ1)(φ2)以及
(φ3)Φ(-x)=Φ(x),
(φ4)当k→+∞时,ck/k2→+∞.
则算子方程存在无穷多解.
证明首先证明(H1).对式(1.2)求Fréchet导数得
I′(θ,x)(x+θy0)=a(x,x)+θa(x,y0)-Φ′(x+θy0)(x+θy0).
(1.3)
取ν∈(2,μ),对式(1.2)(1.3)整理并化简得
(1.4)
对任意x,y∈Z,有
(1.5)
存在常数M1>0,并由式(1.4)(1.5)和条件(φ1)得
(1.6)

(1.7)
存在常数M2,M3>0,并由式(1.4)(1.6)(1.7)得
(1.8)
那么由式(1.8)得
(1.9)
设(θk,xk)∈[0,1]×Z,使得I(θk,xk)有界,‖I′(θk,xk)‖→0,则‖xk‖有界,存在子序列,不妨仍记为xk且xk在Z中弱收敛于x0,在X中xk→x0,θk→θ0.对任意x,φ∈Z,有
I′(θ,x)φ=a(x,φ)-(▽Φ(x+θy0),φ)X.
(1.10)
a(xk,φ)=(▽Φ(xk+θky0),φ)X+I′(θk,xk)φ.
(1.11)
由式(1.10)(1.11)得
a(x0,φ)=(▽Φ(x0+θ0y0),φ)X.
a(xk-x0,φ)+λ0(xk-x0,φ)X=I′(θk,xk)φ+(▽Φ(xk+θky0)-▽Φ(x0+θ0y0),φ)X+λ0(xk-x0,φ)X.
对于任意x,y∈Z,成立
(x,y)=a(x,y)+λ0(x,y)X.
因此

即I满足(PS),故(H1)得证.
下面证明(H2).已知
由式(1.5)得
由式(1.9)得
又因为存在常数b>0,使得|I(θ,x)| (H3)的证明过程与文献[3]中引理3.2类似,故不再赘述. 下面证明(H4).由条件(φ2)知,存在常数C1,C2使得 因此关于式(1.2)有 故(H4)得证.由引理1知,对I(1,x)有两种情形,若情形(ⅱ)成立,经计算可得 ck≤Mk2, 其中M>0,k∈N*.易知,这同条件(φ4)矛盾,因此I有一个逼近无穷的临界值序列,故定理1得证. 考虑二阶哈密顿系统: (2.1) x(0)-x(1)=0, (2.2) (2.3) 令x(t)=u(t)+z(t),其中z(t)=t(a1+a2t+a3t2)ai∈Rn,i=1,2,3满足式(2.2)(2.3),则有u(t)满足 (2.4) u(0)-u(1)=0, (2.5) (2.6) 定理2设V,f满足以下条件: (V1)V∈C2(R2,R),且V(-x)=V(x). (V2)存在p>2,r>0,对任意x∈Rn且|x|≥r,有 0 (V3)存在M>0,对任意t∈(0,1)有 |f(t)|≤M. 对任意的x0∈Rn,(2.1)-(2.3)有无穷多解. 由文献[4]的命题7.1.1[4]105和命题7.3.1[4]117,知σ(A)=σd(A)有下界 D(|A|1/2)≡H1([0,1],Rn)≡Z. 因此,对于u∈D(A)和v∈Z,设双线性型 对于u∈Z,由式(2.5)(2.6)得 对于u∈Z,I:[0,1]×E→R,令 证明详细证明过程见文献[5]的定理B. 定理2的证明首先证明(φ1).存在M4,M5>0,并由条件(V2)得 V′(t,x)·x≥pV(t,x)-M5. 对上式关于x积分得 V(t,x)≥M4|x|p-M5. 故(φ1)得证. 然后证明(φ2).对于u∈Z,有 由条件(φ1),知 故(φ2)得证. 对于(φ4),从文献[6]中引理5.1知,存在G∈C2(R,R),使得 (1)G′=g是奇函数; (2)G(0)=g(0)=g′(0)=0; (3)g在[0,+∞)上是增的; 对于u∈H1([0,1]),令 对于u=(u1,…,un)∈Z,令 其中Gk,Zk如第一部分所述,对于任意k∈N*,有 ck≥dk-c. 所以欲证(φ4),只需证当k→∞时,dk/k2→∞. (2.7) x(0)-x(1)=0, (2.8) (2.9) 则对任意y∈H1([0,1],R),有 由H1([0,1],R)中的内积,知 (2.10) 对式(2.10)化简,则对任意y∈H1([0,1],R)有 其中q1(t)=g′(u(t)). 根据文献[4]的引理2.6.4[4]28知x满足式(2.8)(2.9)和 (2.11) 对式(2.11)进行上述变换,得关于φ(t)的表达式如下: φ′(t)=cos2φ(t)+q(t)sin2φ(t),t∈(0,1). (2.12) 由式(2.8)(2.9)得 φ(0)=φ(1). φ(1,q1,φ(1))=ψ(1)∈(mπ+φ(1),mπ+π+φ(1)). φ(1,q1,φ(1))>φ(1,q2,φ(1))=mπ+φ(1). 因此,下面只需证φ(1,q1,φ(1))<(m+1)π即可. 0≤τ1 因为g(u)是奇的,所以t2-t1=t3-t2=…=tm-tm-1,且u(ti+Δt)=u(ti-Δt),其中0<Δt 由(2.7)-(2.9)和G,g的性质有 同理, 因此 (2.13) 下面只需证当k→∞时, (2.14) (2.15) (2.16) 对式(2.16)分部积分得 (2.17) 由式(2.15)得 (2.18) 已知u=v,则 (2.19) 由式(2.13)(2.17)-(2.19)和G的性质并计算得 |g(v(t))|≤c|v(t)|,及 本文主要研究了一类二阶哈密顿系统解的多重性问题.使用布尔(Bolle)等提出的连续性方法得到该系统无穷多解的存在性.扩充了二阶哈密顿无穷多解存在性的相关研究内容,也为光学、天体力学、量子力学等领域相关研究提供了理论基础.

2 定理1的应用
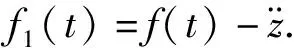

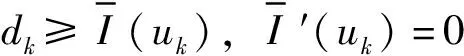
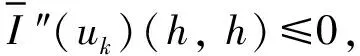



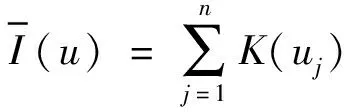
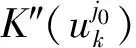
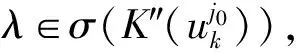



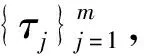
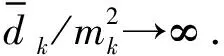
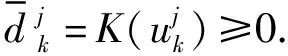

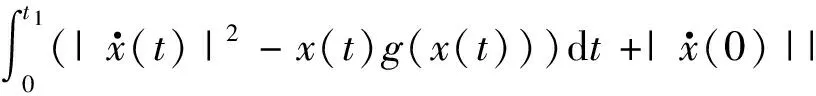

3 结语
