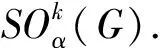给定度序列的连通图类的k阶Sombor指数

2024-05-13王星雨耿显亚

洛阳师范学院学报 2024年2期

王星雨,耿显亚

(安徽理工大学数学与大数据学院,安徽淮南 232001)

0 引言

G是具有顶点集合V(G)和边集合E(G)的图.令d(u)=dG(u),N(u)=NG(u)〔顶点u∈V(G)的邻域集〕.如果V(G)=(v1,v2,…,vn),di=d(vi),1≤i≤n,则π=(d1,d2,…,dn)被称为G的度序列.通常假设d1≥d2≥…≥dn,定义Γ(π)为度序列π的连通图类.有n个顶点和(n+c-1)个边的连通图被称为c圈图.

近期,Gutman提出了一个几何方法来解释基于度的图不变量[1],通过这种方法,介绍了Sombor指数,定义为:

后期,这种图不变性引起了广泛注意,在一系列研究中确定了它的数学性质.

对原始Sombor指数进行修改,使其变为更一般的Sombor指数[2-10],定义为:

其中α≠0是实数.显然SO0.5(G)=SO(G).

确定Γ(π)的元素和图不变量是很重要的.一些这样的研究已经发表在相关文献上[11-15].这些结果表明,在许多情况下,极值图是BFS型的.

1 定理的证明

定义1[10]G是一个连通图.G被称为BFS图,若V(G)中存在顶点v1v2…vn满足:

(1)d(v1)≥d(v2)≥…≥d(vn)和h(v1)≤d(v2)≤…≤d(vn),h(vi)是vi到v1的距离.

(2) 令v∈N(u)N(w),z∈N(w)N(u)满足h(v)=h(u)+1,h(z)=h(w)+1.如果uw,则vz.

定义2[14]对于一个给定的c圈度序列π=(d1,d2,…,dn),dn=1,n≥3,如果G是一个BFS图满足{v1,v2,v3}构成一个三角形,当c≥1时,则G被称为特殊极图.

定义3[10]给定度序列π=(d1,d2,…,dn),dn=1,G被称为连通图类的k阶精确极图,如果G

定理2任意圈度序列,有:

(1)TM(π)是c=0时的精确极图;

(2)UM(π)是c=1时的精确极图;

(3)BM(π)是c=2时的精确极图.

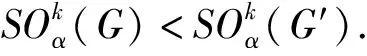
下面证明定理1、定理2.首先引入一个定义在正实数范围内的对称二元函数f(x,y),称f(x,y)是递增的(或递减的),如果满足

f(x1,x2)+f(y1,y2)≥(≤)f(y1,x2)+f(x1,y2),任意x1≥y1>0,x2≥y2>0,当x1>y1,x2>y2时,上式严格不等.

Wang[15]给出了将连通图和对称二元函数f(x,y)联系在一起的连接函数

定理1和定理2的证明还需要引入两个引理.

引理1[14]任意给定度序列π=(d1,d2,…,dn),dn=1,在连通图类Γ(π)中,存在一个特殊极BFS图G,使得当f(x,y)递增时,Mf(G)是最大的,当f(x,y)递减时,Mf(G)是最小的.

引理2[14]给定c圈度序列π=(d1,d2,…,dn),dn=1.在连通图类Γ(π)中

(1) 若c=0,当f(x,y)递增时,TM(π)有最大Mf(G),当f(x,y)递减时,TM(π)有最小Mf(G);

(2) 若c=1,当f(x,y)递增时,UM(π)有最大Mf(G),当f(x,y)递减时,UM(π)有最小Mf(G);

(3) 若c=2,当f(x,y)递增时,BM(π)有最大Mf(G),当f(x,y)递减时,BM(π)有最小Mf(G);

8月20日，由雷邦斯生物技术（北京）有限公司及雷邦斯集团成员企业爱必施农业技术（北京）有限公司主办、中国农资传媒独家策划的世界橙油共享发布会暨微生物工艺提取活性腐殖酸发布会在北京举行，雷邦斯生物技术（北京）有限公司总经理冉峰、常务副总经理褚晖，雷邦斯集团企业、合作伙伴及多家行业媒体代表等出席活动。发布会上，与会嘉宾就橙油的应用与发展、微生物工艺提取活性腐殖酸的工艺和应用优势等内容进行了分享和交流。

证明假设x1>y1,x2>y2,易得