利用“两点之间线段最短”解决最值问题

陈礼弦

摘 要：文章立足于初中数学教学实践，结合典型实例详细论述了利用“两点之间线段最短”结论解决最值问题的主要思路，旨在于为初中数学教学提供崭新思路.与此同时，通过解题活动，提高学生分析问题和解决问题的能力，提升其数学核心素养.

关键词：初中数学；核心素养；线段最短；最值問题

中图分类号：G632 文献标识码：A 文章编号：1008-0333（2024）08-0013-03

与线段之和或差有关的几何最值问题是中考热点，通常以中考压轴题的形式出现，具有一定的选拔性功能，对学生而言具有一定的难度.这类问题是教学的难点，是核心素养的重点考查对象[1].在初中数学教学中，教师该如何引导学生利用“两点之间线段最短”解决最值问题呢？根据笔者多年的教学经验，只要弄清三个数学模型，学生在解决这类问题时便会收到事半功倍之效.

1 模型1 “一线两点”型

1.1 利用“两点之间线段最短”求线段和的最小值

1.1.1 点在直线两侧时，线段和的最小值问题

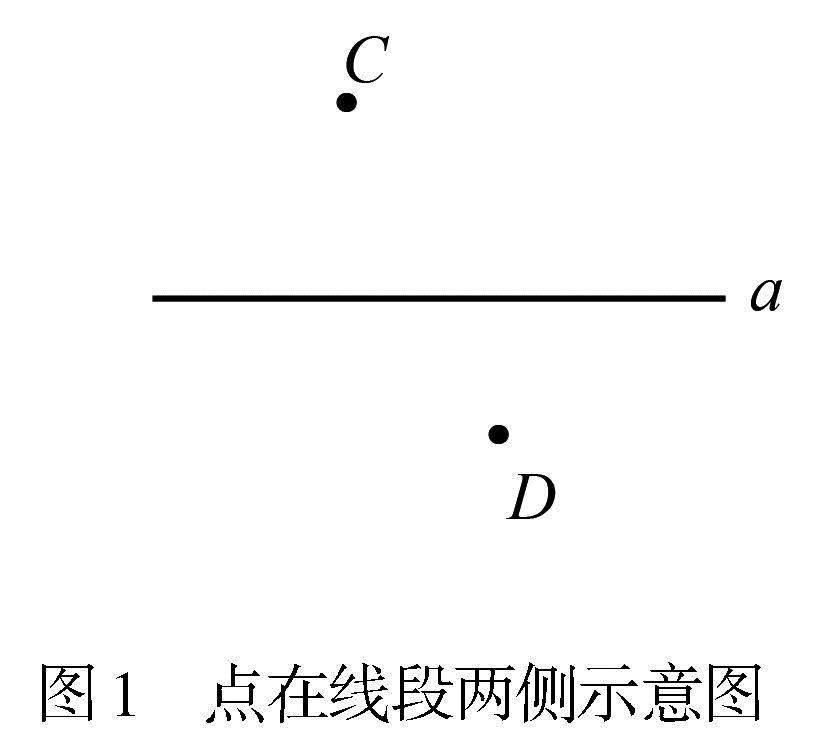
例1 如图1，两定点C、D位于直线a两侧，在直线a上找一点M，使得MC+MD的值最小.

解析 如图2，连接CD交直线a于点M，点M就是所找的点.理由是“两点之间线段最短”.

1.1.2 点在直线同侧时，线段和的最小值问题

例2 如图3，两定点C、D位于直线a的同侧，在直线a上找一点M，使得MC+MD的值最小.

解析 如图4，作点D关于直线a的对称点D′，连接CD′与直线a交于点M，点M就是所找的点.显然，将直线a同侧两个定点转化为两侧两个定点，便可以利用点在直线两侧时线段和的最小值问题的处理方法解决最值问题.

1.1.3 模型应用

例3 如图5，已知△DEF中，DE=DE，GH是DE的垂直平分线，M是GH上一动点，点N是EF的中点，如果DE=13，△DEF的周长是36，求EM+MN的最小值.

解析 如图6，连接DM，MN.因为DE=DF=13，△DEF的周长是36，所以EF=36-2×13

1.2 利用“两点之间线段最短”求线段差最大值

1.2.1 点在直线同侧时，线段差的最大值问题

例4 如图7，两定点M，N位于直线b的同侧，在直线b上找一点H，使得|HM-HN|的值最大.

解析 如图8，连接MN并延长与直线b交于点H，点H就是所找的点.

1.2.2 点在直线两侧时，线段差的最大值问题

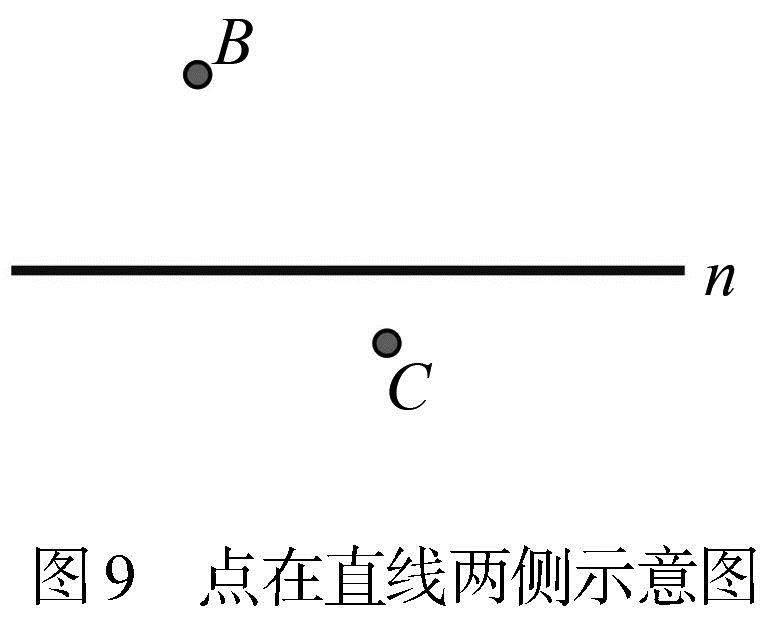
例5 如图9，两定点B，C位于直线l的两侧，在直线n上找一点M，使得︱MB-MC|的值最大.

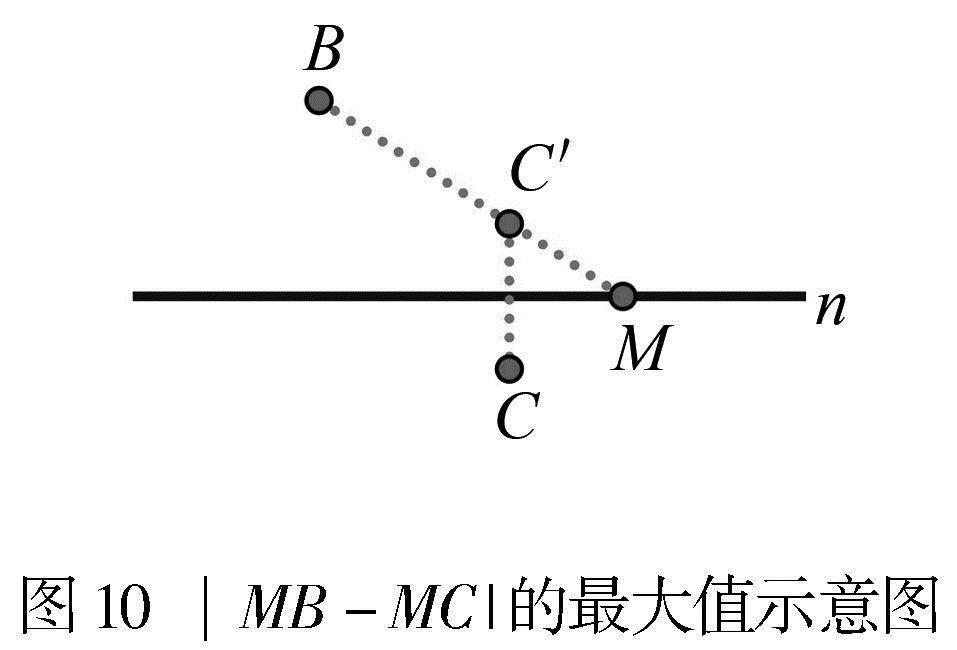
解析 如图10，作点C关于直线n的对称点C′，连接BC′并延长与直线n交于点M，点M就是所找的点.显然，将已知直线两侧的两个定点转化为同侧的两个定点，便可以用同侧线段差最大值的方法解决问题.

1.2.3 模型应用

例6 如图11，在正方形DEFG中，DE=6，点I是对角线EG上靠近点E的三等分点，点H是DG边上的一点，且GH=2.J为EF上一点，连接JH、JI.

①在图中画JH-JI的最大值时点J的位置（为区分点J，请用字母J标记）；

②求JH-JI的最大值.

解析 如图12，连接HI并延长交BC于点J′，则点J′即为所求作的点.

2 模型2 “一定两线”型

2.1 利用“两点之间线段最短”求周长最小值

例7 如图13，点D是∠BOC的内部一定点，在OB上找一点N，在OC上找一点M，使得△DMN的周长最小.

解析 如图14，分别作点D关于OB、OC的对称点D′、D″，连接D′D″，交OB、OC于点N、M，点N、M便是所找的点.

2.2 利用“两点之间线段最短”求线段和的最小值

例8 如图15，点M是∠DEF的内部一定点M，在ED上找一点A，在EF上找一点B，使得MB+AB的值最小.

解析 如图16，作点M关于EF的对称点M′，过点M′作ED的垂线，分别与ED、EF交于点A、B，点A、B是所找的点.

2.3 模型应用

例9 如图17，在Rt△BCD中，∠BCD=90°，DC=6，BC=8，DE是∠BDC的平分线.若M、N分别是DC、DE上的动点，求NC+NM的最小值.

3 模型3 “一定长，两定点”型

3.1 异侧线段和最小值问题

例10 如图19，已知直线a∥b，直线a和直线b之间距离为c，在直线a和直线b上分别找点A、B两点，使AB⊥a，且MA+AB+BN的值最小.

解析 如图20，将点M向下平移c个单位到M′，连接M′N交直线b于点B，过点B作BA⊥l1于点A，点A、B两点是所找的点.

3.2 同侧线段和的最小值问题

例11 如图21，在直线a上找A、B两点（A在B左侧），使得AB=k，且MA+AB+BN的值最小.

解析 如图22，将点M向右平移k个单位到点M′，作点M′关于直线a的对称点M″，连接M″N交直线a于点B，将点B向左平移k个单位到点A，A、B两点是所找的点.

4 结束语

在初中数学教学中，教师引导学生经历并弄清“一线两点”型、“一定两线”型、“一定长，两定点”型最值问题的求解方法，不仅能够提高学生分析问题和解决问题的能力，而且能够使教师的教学效果达到“教是为了不教”之目的[2].

参考文献：

［1］ 孔令志， 马学斌. 2020年中考数学压轴题高频热点问题赏析（4）线段和的最小值问题：两点之间线段最短[J].中小学数学（初中版）， 2020（12）：37-40.

[2] 叶婷婷. 初中几何“线段最值”问题的求解策略[J].启迪与智慧（上）， 2020（4）：96.