敏捷转弯伞弹系统动力学建模与分岔特性分析

2024-05-09周洪淼于剑桥于勇

航空学报 2024年7期

周洪淼，于剑桥，于勇

北京理工大学宇航学院，北京 100081

传统弹箭类飞行器由于几何外形、气动布局等条件的约束，正面临机动性能、突防能力等性能上的瓶颈，逐渐难以满足现代军事斗争的高强度需求。如果能在保持传统弹箭类飞行器高速高精度优势的基础上附加极短时间超机动敏捷转弯能力，则可以使弹箭类武器更好地应对复杂、多变的战场环境。在高速高动态条件下实现导弹超机动敏捷转弯，需要超量级的机动载荷支持。传统弹箭设计思路中采用的气动力控制装置、直接力控制装置（Reaction-jet Control System，RCS）或推力矢量装置（Thrust Vector Control，TVC）［1-3］不具备提供超量级机动载荷能力，导弹转弯半径通常在50 m 以上，转弯时间>2 s。因此，通过加装其他控制装置，在维持弹箭高速飞行气动构型不变的前提下提供弹箭超机动敏捷转弯所需的超量级机动载荷成为了一个新的研究方向。

航空领域的柔性面主要包括各类降落伞及翼伞，具有质量轻、折叠后尺寸小、空间利用率高、能产生大量级气动力等优点。目前，通过加装柔性面的方式实现对导弹的控制已有相关的研究成果，主要集中在利用圆形降落伞对末敏弹进行减速减旋及稳定姿态［4-7］。但是传统的圆形降落伞由于缺乏主动控制能力且仅能安装在导弹尾部，对导弹主要起到减速作用，难以利用其产生导弹敏捷转弯所需的法向控制力和控制力矩。

翼伞是一种前缘有切口，利用冲压空气保持一定形状的柔性飞行器。可操纵性是翼伞与传统降落伞的最大区别，通过拉动连接翼伞后缘的两根操纵伞绳改变气动力和气动力矩，从而控制翼伞的飞行姿态。翼伞广泛应用于飞行器回收、精确空投等领域［8-10］。如果在导弹弹体侧面加装可控翼伞作为柔性控制面，在导弹执行超机动敏捷转弯时将折叠翼伞弹出，使其充气展开，提供导弹姿态调整所需超量级法向机动载荷，则有望实现导弹快速、小半径、大角度敏捷转弯。本文由此提出由导弹、翼伞组成的伞弹系统，如图 1 所示。伞弹系统的战术意义包括：①减小敏捷转弯半径；② 减小敏捷转弯时间；③完成超机动动作后即可抛掉翼伞系统以减轻质量，在发动机作用下进入末端加速攻击阶段。

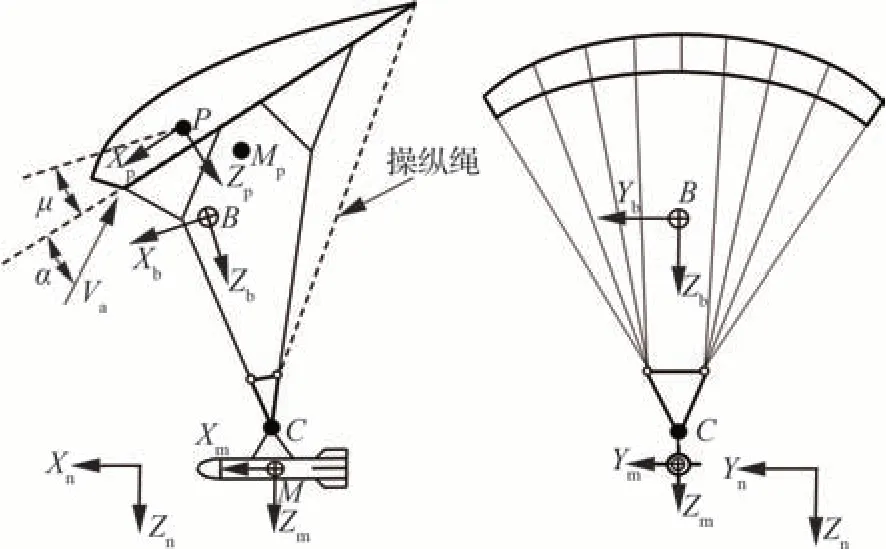
图1 伞弹系统示意图Fig.1 Schematic of parafoil-missile system

动力学建模是飞行器设计的基础，目前针对翼伞系统的动力学建模已经有了较多研究。针对翼伞多体系统的动力学建模主要分为3 类：一是单刚体六自由度模型，以文献［11-13］为代表，该种建模方法关心的是翼伞系统整体的运动状态，包括运动轨迹及运动姿态，但是无法获得更多运动参数信息；二是考虑翼伞与载荷之间的约束连接关系，文献［14-15］将翼伞与无人机之间的连接关系简化为带有滚转约束的铰接，推导出系统的8 自由度模型，文献［16］则考虑了翼伞与载荷之间的相对滚转运动，推导出系统的9 自由度模型。目前关于翼伞载荷系统的动力学建模已经有比较成熟的方法。

Prakash等［16-17］利用分岔分析与连续算法，分别对翼伞系统纵向平面内的4 自由度动力学模型及空间9 自由度动力学模型进行分岔分析，研究了在不同襟翼偏转量下，安装角对翼伞滑翔及雀降性能的影响。Yang等［18］基于小扰动线性化假设推导了翼伞系统的小扰动线性化方程，分析了绳长、安装角、翼伞下反角对系统运动稳定性的影响，但是该方法无法准确揭示系统的非线性动力学现象。对翼伞-导弹系统而言，其动力学具有快时变、强非线性的特点，小扰动线性化假设难以适用。

翼伞气动性能的研究早期使用风洞试验，美国NASA 与Notre Dame 大学在20 世纪60 年代进行了一系列的风洞试验［19］，但是风洞试验成本较高，目前多采用计算流体力学（Computational Fluid Dynamics，CFD）方法进行研究。孙青林等［20］对襟翼偏转气动性能进行数值模拟实现对翼伞气动模型的修正，朱虹等［21］综合考虑翼伞前缘切口及后缘下偏的影响，实现了翼伞气动力的精确计算。但是上述研究中，翼伞的来流速度在10 m/s 左右，在如此低速飞行条件下难以满足导弹高速高动态敏捷转弯需要。

本文首次提出通过导弹加装可控翼伞作为控制面实现导弹快速、小半径、大角度敏捷转弯。为了可以准确地模拟翼伞-导弹系统的运动状态，给出能够反映翼伞、导弹相对运动的空间9 自由度动力学模型。通过CFD 数值模拟得到翼伞在马赫数0.3～0.5、攻角范围-5°～20°情况下的气动系数。通过纵向平面内的弹道仿真，证明所提出伞弹系统敏捷转弯方案的有效性。利用分岔分析方法研究翼伞-导弹系统动力学特性，得到在不同襟翼偏转角情况下，系统以安装角为变化参数的分岔图，根据分岔结果给出导弹实现最小转弯半径及最大转弯末速所需的安装角及襟翼偏转角参数。

1 动力学建模

提出的翼伞-导弹系统如图 1 所示，系统包括加装在导弹侧面的翼伞、伞绳、伞绳连接点及导弹，以下简称伞弹系统。

定义相关坐标系及参考点如下：{n}为地面惯性坐标系，{p}为翼伞体坐标系，原点位于翼伞压心P，Xp与翼伞参考弦线重合，指向前缘为正，Yp垂直于翼伞纵向对称平面，Zp与Xp、Yp构成右手直角坐标系。{m}为弹体坐标系，原点位于导弹质心M，Xm与弹轴重合，Ym垂直于导弹纵向对称平面。{b}为由翼伞、伞绳、操纵机构构成子系统（以下简称翼伞子系统）的体坐标系，原点位于翼伞子系统质心B，Zb轴位于翼伞子系统纵向对称平面内，与矢量平行，C 点为伞绳汇交点。Mp为翼伞附加质量质心。

翼伞子系统和导弹被视为由C 点铰接的2 个刚体。伞弹系统被视为9 自由度模型，包括连接点C 的3 个惯性位置自由度，以及翼伞子系统和导弹的3 个欧拉转动角度自由度。

1.1 翼伞附加质量模型

对翼伞这种在空气中运动的柔性织物，其密度与空气相当，附加质量对动力学特性的影响无法忽略［22-23］。等效作用在B 点的附加质量力和力矩的计算公式为

矢量叉乘矩阵S(⋅)定义如下：

式中：μ 为翼伞安装角，其大小等于Xp与Xb之间的夹角，翼伞相对导弹抬头为正。安装角表征了翼伞与导弹的相对安装角度。

附加质量矩阵Ia.m.和附加转动惯量矩阵Ia.i.是对角矩阵：

Lissaman和Brown［22］给出附加质量的计算公式为

其中：ρ 为空气密度。其余几何参数意义如图2 所示，t 为翼型厚度；c 为翼伞弦长；b 为翼伞展长。

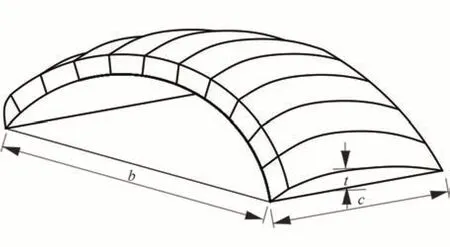
图2 翼伞几何参数Fig.2 Geometric parameters of parafoil

图3 翼伞气动外形参数Fig.3 Aerodynamic shape parameters of parafoil

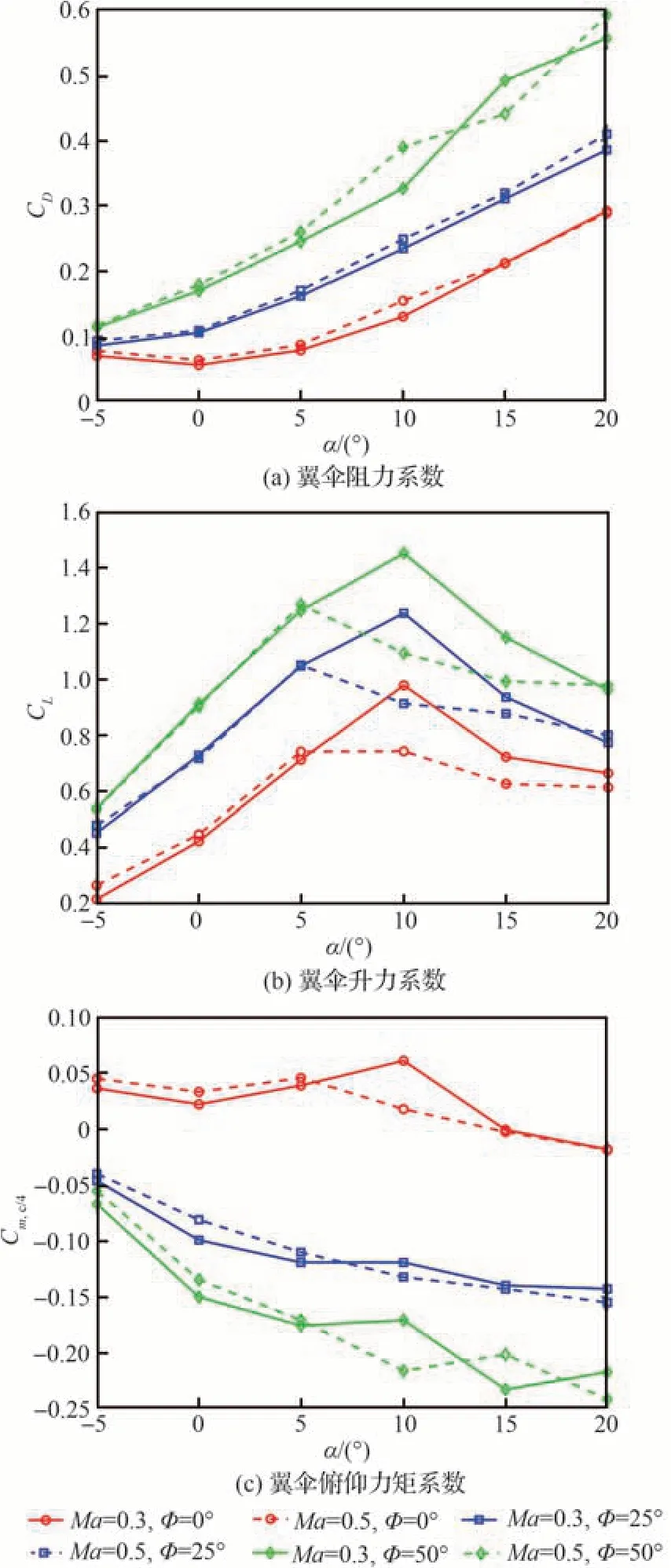
图4 CFD 数值模拟得到的翼伞气动参数Fig.4 Aerodynamic parameters of parafoil obtained by CFD

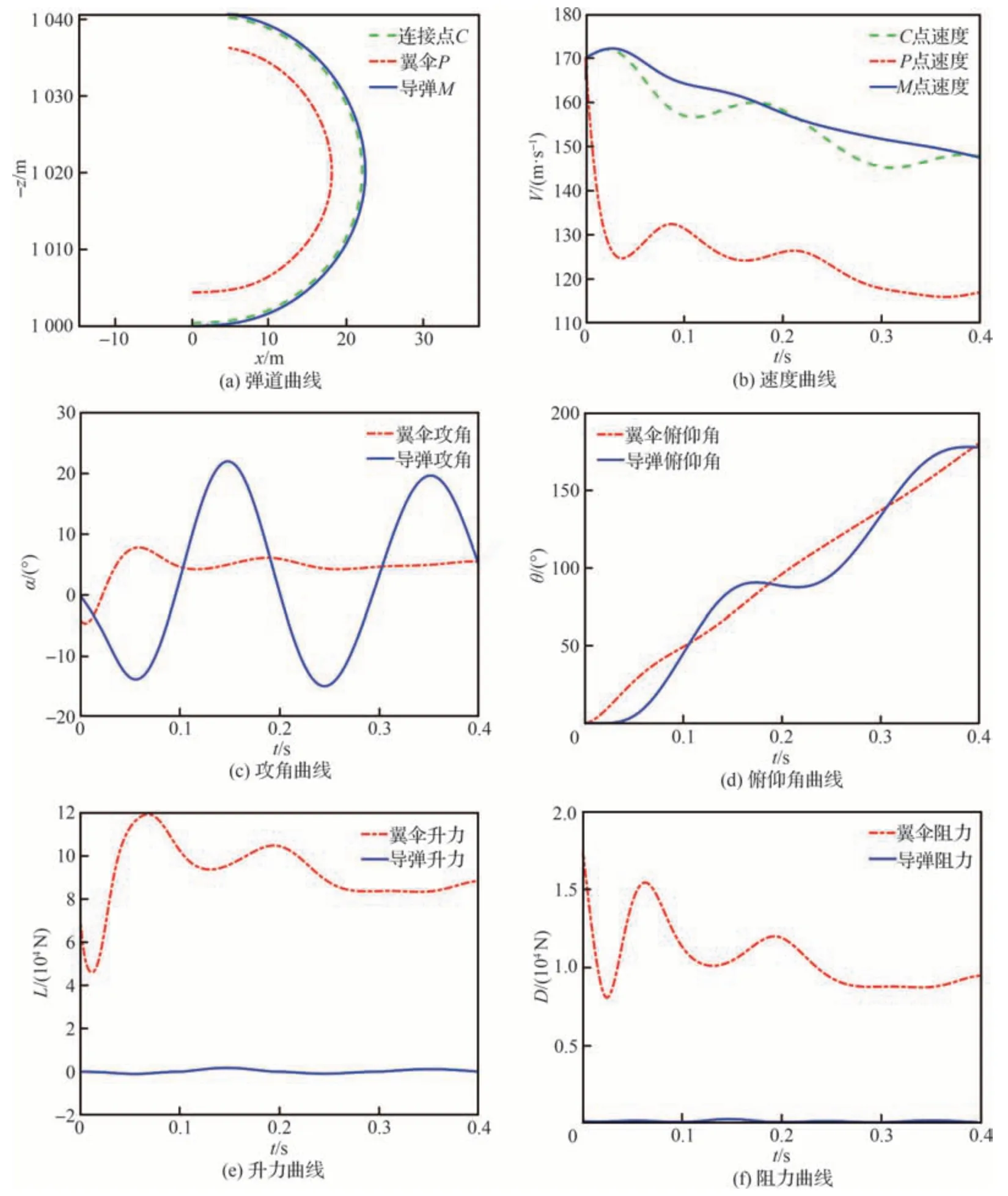
图5 襟翼无偏转仿真结果Fig.5 Results of simulation with no flap deflection

1.2 动力学及运动学模型

伞弹系统9 自由度动力学模型与翼伞载荷系统9 自由度模型基本相同，后者在诸多文献中均有论述［16，24］，本文略去其推导过程，直接给出动力学模型。导弹为轴对称气动外形，翼伞作用时导弹本身不进行姿态控制，发动机推力沿弹体轴向。

C 点的平动运动学方程为

式中：[ xCyCzC]T为C 点在惯性系下的位置坐标为{b}系到{n}系的转换矩阵。

翼伞子系统和导弹的转动运动学方程分别为

式中：θ、ψ、ϕ 分别为翼伞子系统的俯仰、偏航和滚转角；θm、ψm、ϕm分别为导弹的俯仰、偏航和滚转角。式（8）～式（12）共同构成了伞弹系统9 自由度运动模型。

2 翼伞气动参数数值模拟

2.1 翼伞气动外形

翼伞气动外形参考文献［19］中的翼伞模型，如图 3 所示，其中气动弦长c 为2.133 6 m，展长b 为6.400 8 m，弧面下反角β 为9.55°，伞绳R 为4.78 m，前缘切口角度为45°。由于翼伞充气后具有固定形状且伞绳处于张紧状态，翼伞气室内部几乎没有气流，翼伞在小攻角下的气动特性与固定翼型非常相似［18］。对于真实翼伞，伞绳的气动力不可忽略，但对于本文而言，忽略伞绳气动力可以简化分析，并不影响主要的定性分析结论。因此，对翼伞模型做如下简化：①翼伞视为刚体，仅在襟翼偏转时考虑形变；② 伞衣结构不透气；③不考虑翼伞内部流场；④ 忽略伞绳产生的气动力。上述简化可以降低计算成本，缩短数值模拟周期。

共使用3 个不同形态的翼伞模型。翼伞以弦长75%处为轴弯折［19］，即后缘25%的翼尖向下弯折，弯折角度Φ 称为偏转角。其中模型1 襟翼无偏转Φ=0°，模型2 襟翼双侧对称偏转Φ=25°。模型3 襟翼双侧对称偏转Φ=50°。展向两侧偏转量大，展向中部偏转量小。

2.2 流场设置与求解方法

流场计算采用Ansys Fluent21.0，采用密度基求解器，求解时均Navier-Stokes（RANS）方程组［25］。湍流模型选择RNG k-ε 湍流模型［26］，对近壁面逆压梯度变化有较好的捕捉效果，空间离散方式为二阶迎风。

边界条件设置如下：翼伞表面为无滑移壁面；计算域的6 个边界为压力远场，来流马赫数0.5和0.3，压力101 325 Pa。攻角范围为-5°～20°，间隔5°。

气动力系数以来流值为参考条件，参考长度取弦长c，俯仰力矩系数参考点位于距翼伞前缘c/4处。

2.3 CFD 数值模拟结果

CFD 数值模拟得到的翼伞阻力系数CD，升力系数CL和俯仰力矩系数Cm，c/4如图 4 所示。由图 4可知阻力系数随攻角增大而增大，来流速度对阻力系数影响并不明显。襟翼偏转角越大，阻力系数越大。α=0°、Φ=0°时阻力系数有最小值。

升力系数随攻角增大先上升后下降，Ma=0.3时失速攻角出现在5°左右，Ma=0.5 时失速攻角出现在10°左右。襟翼偏转，升力系数增大。Φ=50°时，攻角在5°～10°范围内，升力系数较大。

Φ=0°时，攻角增大，翼伞压心逐渐后移并跨过参考点，Φ=25°及Φ=50°时，翼伞压心始终位于参考点之后。翼伞压心后移导致力矩系数减小。

若仅考虑翼伞在纵向平面内的运动，翼伞的气动力和气动力矩计算公式别为

式中：Sp为翼伞的特征面积；Vp为P 点速度；Cmq为由俯仰角速率引起的俯仰阻尼力矩系数导数；为翼伞空速坐标系到翼伞体坐标系的转换矩阵：

其中：[ upvpwp]T为P 点速度在{p}系下的投影；rCP为矢量在{b}系下的投影。

3 伞弹系统无控弹道仿真

3.1 无控弹道仿真

为了验证伞弹系统可以实现快速、小半径、大角度敏捷转弯，进行伞弹系统无控弹道仿真。导弹参数及气动系数参考文献［1］中提供的数据。伞弹系统参数如表1 所示。

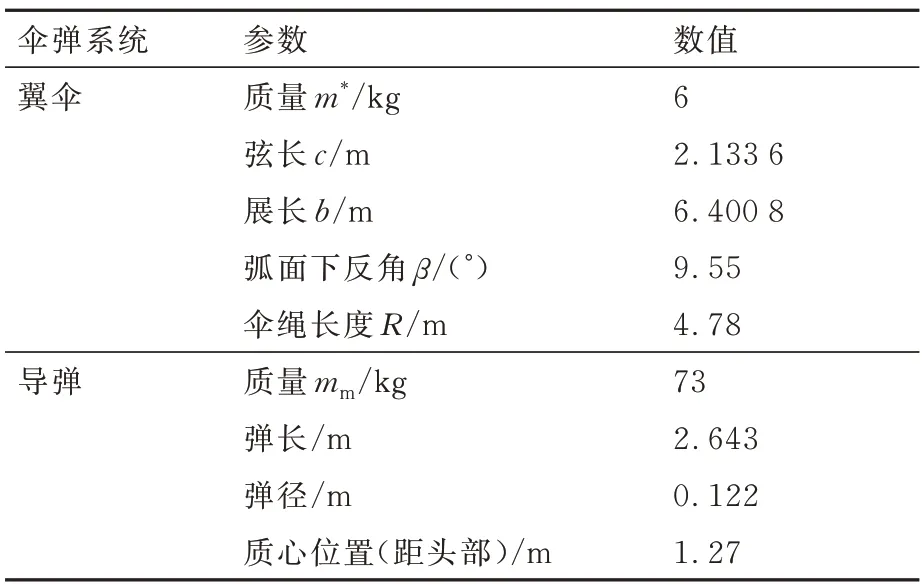
表1 伞弹系统参数Table 1 Parameters of parafoil-missile system

对伞弹系统模型做出如下假设：

1）不考虑翼伞从弹体中弹出、开伞及充气过程。

2）忽略伞绳产生的气动力。

3）翼伞是展向对称的，伞衣充气张满后具有固定形状，除襟翼偏转外视为不可变形刚体。

4）翼伞压心P 与1/4 参考弦线处重合。

5）仅考虑伞弹系统在纵向平面内的运动，不考虑侧向扰动。

导弹推力5 000 N，无舵控，翼伞和导弹的初始速度为0.5Ma，姿态角为均为0°，初始高度1 000 m，翼伞安装角μ=-4°，仿真结束条件为翼伞俯仰角达到180°。Φ=0°情况下弹道曲线，翼伞和导弹的速度、攻角、俯仰角、升力、阻力曲线如图 5 所示。由图 5 可知伞弹系统在0.396 s内完成了纵向平面内敏捷转弯，转弯半径20.33 m，导弹速度由170 m/s 降至149.44 m/s，速度损失比较小。翼伞攻角变化幅度很小，并最终稳定在5°左右，导弹攻角在-14°～22°之间振荡。导弹俯仰角变化与翼伞俯仰角变化大致相同，翼伞俯仰角速度最终趋于稳定值。翼伞产生的气动力远大于导弹的气动力，其中翼伞产生的升力主要提供伞弹系统在纵向平面内作近似圆周运动的向心力。

3.2 不同襟翼偏转角情况仿真对比

为了研究翼伞不同襟翼偏转角对伞弹系统运动的影响，在其余仿真条件相同的情况下，对比了Φ=0°，25°，50°情况下导弹弹道，导弹速度，翼伞攻角及翼伞升力系数变化曲线如图 6 所示。

表2 给出了不同襟翼偏转角情况下伞弹系统敏捷转弯主要性能数据，包括导弹转弯半径、转弯末速及转弯时间对比。Φ=50°时导弹转弯半径最小，同时转弯时间最短，Φ=0°时导弹转弯末速度最大。Φ=0°时翼伞攻角发生了一定范围内的振荡，Φ=25°及Φ=50°时翼伞攻角较快收敛于平衡状态。

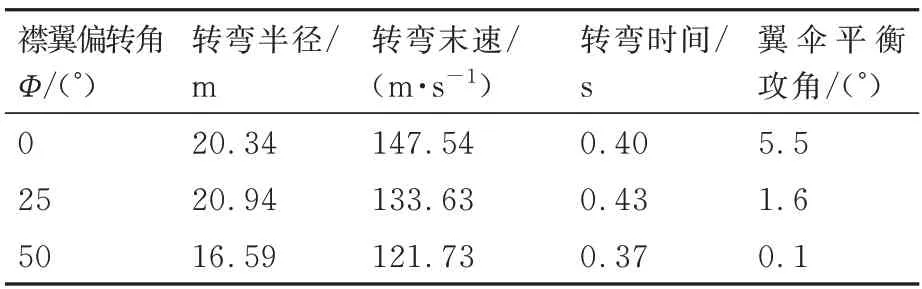
表2 不同襟翼偏转角伞弹系统敏捷转弯性能对比Table 2 Comparison of agile turn performance of parafoil-missile system at different flap deflections

在伞弹系统完成敏捷转弯后，即可抛掉翼伞子系统，导弹恢复舵控，依据导引规律进入末端加速攻击阶段。

3.3 仿真结果分析

对于纵向平面内机动的导弹而言，忽略舵面产生的控制力，弹道倾角γ 满足如下方程［27］：

式中：W 为导弹重力；L 为导弹受到的升力。对伞弹系统而言，由于翼伞产生的气动力远大于导弹产生的气动力、导弹推力及导弹重力，因此下述关系成立：

导弹转弯半径RT满足：

式中：LPM为P 点和M 点之间的距离。由式（22）可知：

图6（d）给出了翼伞升力系数变化曲线：

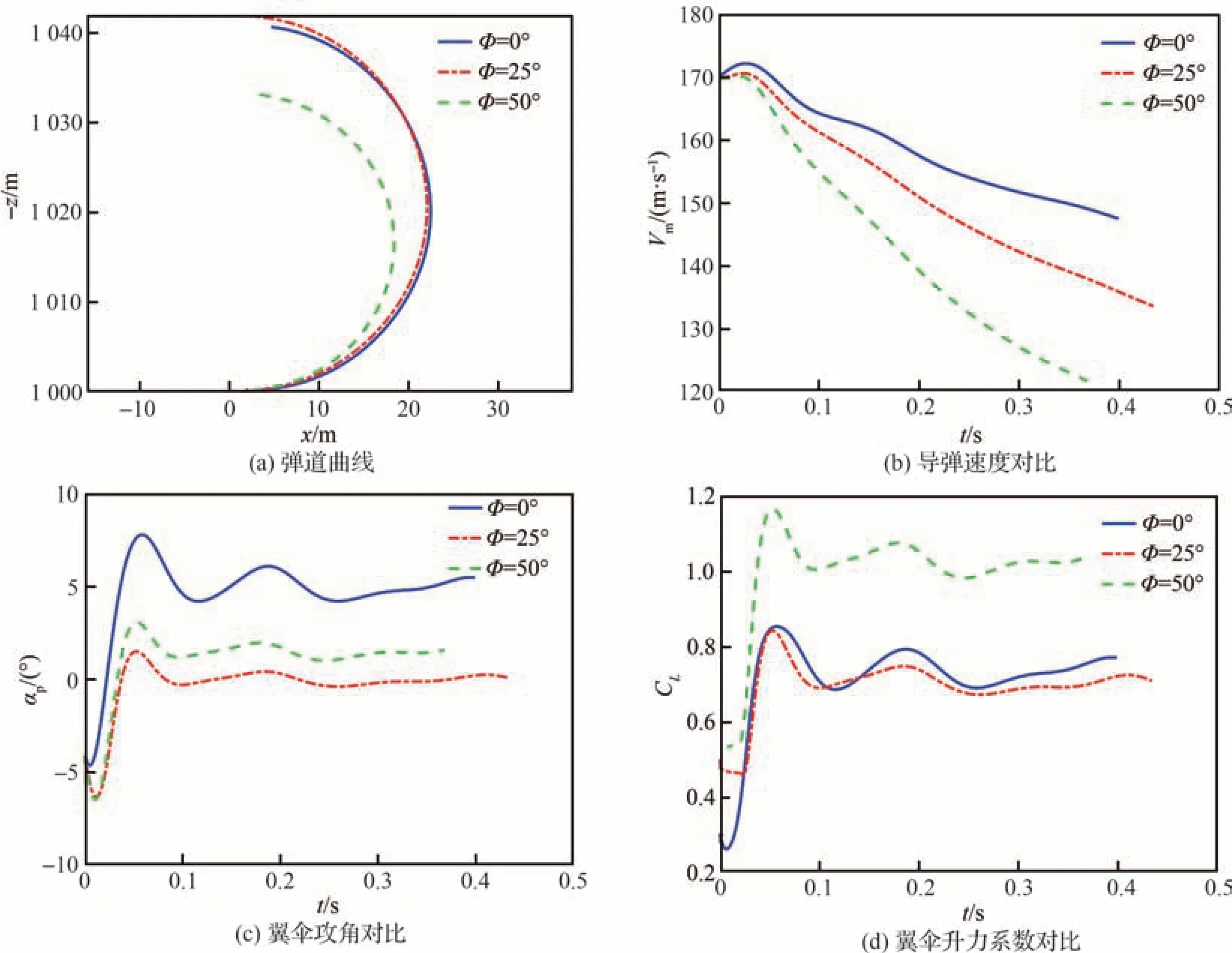
图6 不同襟翼偏转角仿真结果对比Fig.6 Comparison of simulation results at different flap deflections

导弹速度满足如下方程：

由于翼伞产生的阻力远大于导弹产生的阻力及导弹重力，导弹攻角α 是小量，因此下述关系成立：

LPM/RT近似为常数，因此，

翼伞阻力系数越大，导弹转弯末速度越小，由图 4（a）翼伞阻力系数在攻角0°～6°范围内满足

翼伞的升力系数和阻力系数分别是影响导弹敏捷转弯半径和转弯末速的主要因素。如果能够将翼伞平衡攻角配置在翼伞升力系数最大值点（Φ=50°，αp=5°～10°），或阻力系数最小值点（Φ=0°，αp=0°），则可以进一步提高伞弹系统敏捷转弯性能。

4 伞弹系统非线性动力学分岔分析

4.1 分岔分析

分岔现象是非线性动力学系统特有的现象，对非线性系统的定性分析具有十分重要的作用。对于含参数动力系统

式中：x ∈Rn称为状态变量；λ ∈Rm为分岔参数。当参数λ 在Rm内连续变化时，若系统式（32）的平衡状态位置、类型以及稳定性在λ=λ0处突然发生变化，则称系统式（32）在λ=λ0处出现分岔，称λ0为分岔值，(x，λ0)为分岔点。系统的相空间拓扑结构随参数λ 变化的图形称为分岔图。分岔可以分为静态分岔和动态分岔，其中平衡点的个数和稳定性随参数变化为静态分岔，极限环是动态分岔的主要研究内容。

系统式（32）在平衡点(x0，λ0)出现静态分岔的必要条件为平衡点(x0，λ0)处的雅克比矩阵Dxf(x0，λ0)至少存在一个零特征值，分岔点的类型同样可以根据雅克比矩阵的特征值判断。对于高维非线性系统，求解系统平衡点的解析解是十分困难的，数值方法是研究高维系统分岔问题的主要方法，该方法通过连续算法追踪系统解曲线随分岔参数的变化，同时通过判断解的特征值变化规律判断系统的稳定性及分岔点的位置和类别。

伞弹系统动力学方程（8）、（9）是典型的高维非线性系统。本文仅研究伞弹系统在纵向平面内的运动特性，因此将侧向运动状态变量置0，同时为了进一步简化模型，忽略系统受到的重力作用。伞弹系统纵向平面内的动力学方程可整理为式（32）形式，其中状态变量x=[uCwCwCq qmθmb]T。θmb为Xm与Xb之间的夹角，Xb由顺时针转向Xm为正，θmb满足下述方程：

安装角μ 对翼伞载荷系统的平衡攻角有显著的影响［16-17］，本文以安装角μ 为连续变化参数，研究在不同襟翼偏转角Φ 情况下，伞弹动力系统相空间的变化规律，即参数λ=[ Φ μ ]T。为避免翼伞初始攻角落入不合理区间，考虑安装角变化范围μ ∈(-5°，0°) 。本文使用非线性数值分析工具MATCONT［28］进行分岔分析。

图7给出了不同襟翼偏转角Φ 情况下，翼伞平衡攻角αp随安装角μ 变化的分岔图。图中三支稳定平衡分支均在首次遇到Hopf分岔点后失去稳定性。表3 给出三支稳定平衡分支在首次遇到Hopf分岔点时雅克比矩阵特征值及第一李雅普诺夫系数l1。在Hopf分岔点处特征值存在一对纯虚根，由于l1>0，Hopf分岔点处生成不稳定极限环。对于其余Hopf分岔点，均有l1>0，略去其具体数值。

表3 Hopf 分岔点参数Table 3 Parameters at Hopf bifurcation

图7 αp 随μ 变化的分岔图Fig.7 Bifurcation diagram of variation of αp with μ

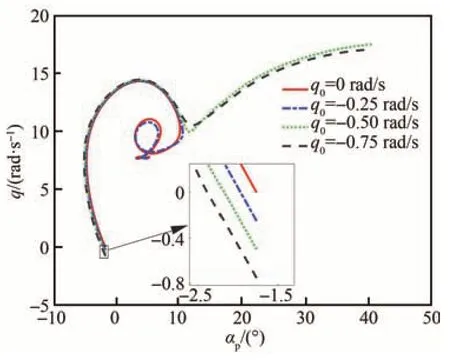
图8 不同初始点相轨线在αp-q 平面上的投影Fig.8 Projection of phase trajectories of different initial states on αp-q plane

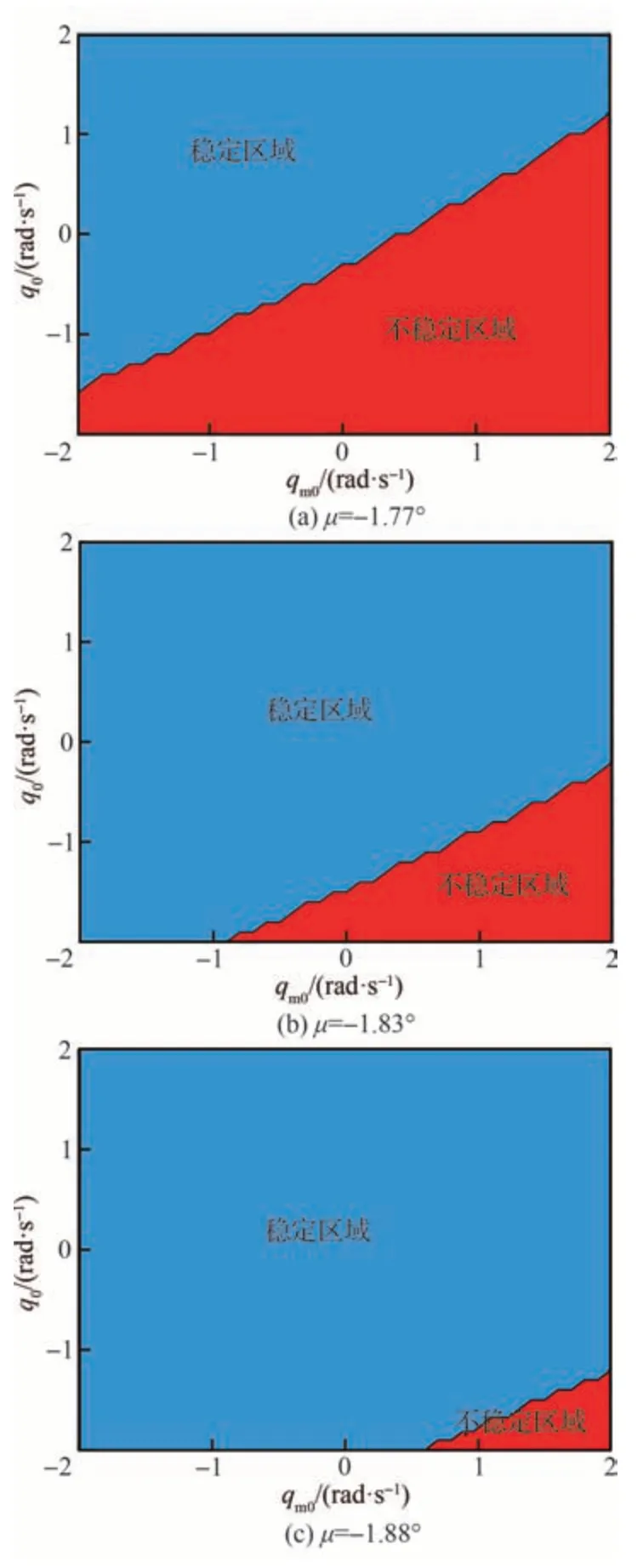
图9 不同安装角μ 情况下稳定平衡点的吸引域Fig.9 Attractive region of stable equilibrium at different μ

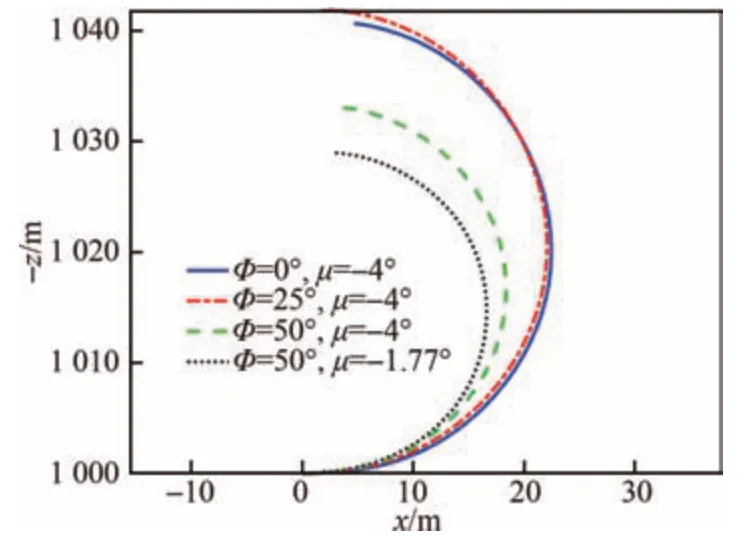
图10 导弹转弯半径对比Fig.10 Comparison of missile turn radii

图11 翼伞攻角对比Fig.11 Comparison of parafoil angles of attack

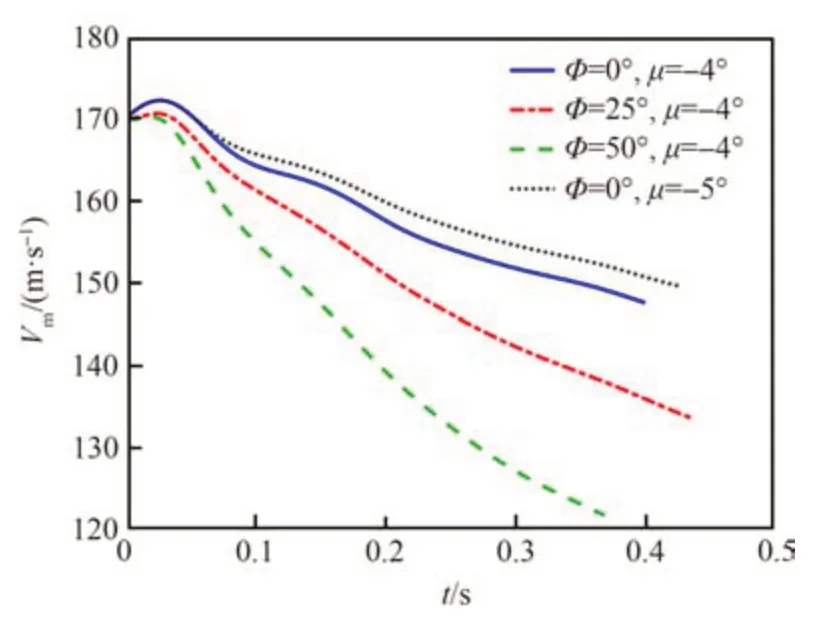
图12 导弹速度对比Fig.12 Comparison of missile speeds

Φ=0°时，稳定的平衡分支对应的安装角μ ∈(-5°，-2.24°)，翼伞平衡攻角范围αp∈(3.37°，8.90°)。

Φ=25°时，稳定的平衡分支对应的安装角μ ∈(-5°，-0.41°)，翼伞平衡攻角范围αp∈（-0.84°，7.03°）。

Φ=50°时，稳定的平衡分支对应的安装角μ ∈(-5°，-1.63°)，翼伞平衡攻角范围αp∈（-0.94°，6.90°）。

由3.3 节分析可知，实现导弹最小转弯半径的理想翼伞平衡攻角区间为αp∈(5°，10°)。当Φ=50°时，安装角μ ∈(-2.13°，-1.63°)对应翼伞平衡攻角αp∈(5°，6.9°)。为避免翼伞平衡攻角落入不稳定区域，安装角应适当远离区间右边界处Hopf 分岔点。综上，选取μ=-1.77°作为实现导弹最小转弯半径的安装角参数。此时对应翼伞平衡攻角αp=5.8°。

实现导弹最大转弯末速的理想翼伞平衡攻角为αp=0°。当Φ=0°时，选取μ=-5°作为实现导弹最大转弯末速的安装角参数。此时对应翼伞平衡攻角αp=3.3°。

以实现上述最小转弯半径及最大转弯末速对应的平衡点为目标平衡点，总结如表4 所示。

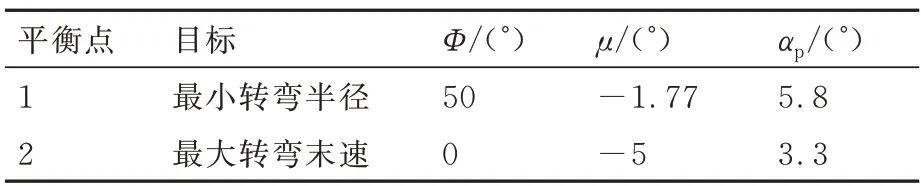
表4 目标平衡点参数Table 4 Target equilibrium parameter

除稳定平衡点外，分岔图中还存在不稳定平衡点。由于Hopf 分岔点存在，系统中还存在不稳定的极限环运动。只有稳定的平衡点对应期望的运动状态。

在上述算例中，运动的稳定性是建立在Lyapunov 意义下的，因而只是局部稳定的。对于具有多个定态（稳定平衡点、不稳定平衡点、不稳定极限环）的系统，仅仅知道局部渐近稳定并不能保证大范围渐近稳定。若期望平衡点的渐近稳定区域很小，则在较小的扰动下系统可能会进入不稳定区域。为此需要计算稳定平衡点的吸引域。

4.2 稳定平衡点的吸引域估计

对于系统式（32），若相空间Rn中的闭集A 满足：以A 内或其某个邻域内的点为初始条件的相轨迹在足够长的时间后可充分趋近于A，则称此集合为吸引集。若相空间Rn中点x0当t →∞时从x0出发的相轨线趋于吸引集A，则点x0的全体称为吸引集A 的吸引域。不能进一步分解的吸引集称为吸引子，常见的吸引子包括稳定平衡点、稳定极限环等。对于渐近稳定平衡点，其吸引域的大小决定了系统的抗干扰能力。

由数学方法很难确定高阶非线性系统平衡点的吸引域，数值计算方法是估计吸引域的有效方法，通过给定不同的初始条件，使用龙格-库塔积分方法求解系统微分方程组，获得系统在给定初始条件下的相轨线，进而判断该点是否位于吸引子的吸引域。

以目标平衡点1 确定的参数为例，给定4 种不同的翼伞初始角速度q0=0，-0.25，-0.50，-0.75 rad/s，伞弹系统其余初始条件与3.1 节相同，进行时域仿真并将相轨线在αp-q 平面上投影，结果如图 8 所示，其中局部放大的图像代表不同的初始状态。由q0=0，-0.25 rad/s 出发的2条相轨线最终趋近于稳定平衡点，由q0=-0.50，-0.75 rad/s 出发的2 条相轨线在越过翼伞失速攻角αp=10°后最终远离稳定平衡点，翼伞攻角在短时间内迅速增大至超过20°。对于超出了气动数据攻角范围的相轨线已不具备实际物理意义，因此并未完全给出。未收敛至稳定平衡点的相轨线是需要避免的运动状态。

伞弹系统在纵向平面内的运动为5 维动力学系统，在此范围内遍历初始条件需要耗费巨大的计算资源，本文研究影响平衡点吸引域的主要因素，分析平衡点吸引域在qm0-q0平面内的投影。

对目标平衡点1，给定初始条件qm0∈(-2，2)，q0∈(-2，2)，其余初始条件与3.1 节相同，绘制在目标安装角附近μ=-1.77°，μ=-1.83°，μ=-1.88°情况下对应稳定平衡点的吸引域，仿真结果如图 9 所示，此时稳定平衡点在qm0-q0平面内的投影分别为 (5.40，5.40)，(5.43，5.43)，(5.45，5.45)。其中稳定区域代表系统状态被稳定平衡点吸引，否则为不稳定区域。由图 9 可知随安装角减小，不稳定区域逐渐缩小，稳定区域增大，系统对初始翼伞及导弹的角速度扰动敏感性减弱，抗干扰性增强。安装角μ=-1.88°时，对应的翼伞平衡攻角αp=5.77°，与平衡点1 对应翼伞平衡攻角相比并未发生较大变化。

对目标平衡点2，给定初始条件qm0∈(-2，2)，q0∈(-2，2)，其余初始条件与3.1 节相同，在目标安装角μ=-5°附近其平衡点吸引域在qm0-q0平面内的投影均为稳定，略去其吸引域图像。

给定由目标平衡点1 确定的系统参数进行伞弹系统弹道仿真，其余初始条件与3.1 节相同，弹道曲线与3.1 节中的仿真结果对比如图 10 所示，导弹转弯半径进一步减小为14.50 m。翼伞攻角变化曲线如图 11 所示，翼伞攻角在5.2°上下发生一定范围内振荡，振幅逐渐衰减且大部分仍处于期望翼伞攻角范围内。翼伞攻角最终稳定在3.5°左右。由式（29）可知，增加导弹推力P 可以进一步增大导弹转弯末速。事实上，当推力P 增大至10 500 N时，在由目标平衡点2 确定的系统参数条件下，导弹转弯速度可基本维持不变。

给定由目标平衡点2 确定的系统参数进行伞弹系统弹道仿真，其余初始条件与3.1 节相同，导弹速度曲线与3.1 节中的仿真结果对比如图 12所示，导弹转弯末速为149.6 m/s。导弹速度在敏捷转弯过程中整体略大于Φ=0°、μ=-4°参数情况。

由以上分析可知，通过改变翼伞安装角及翼伞襟翼偏转角，可以使导弹实现最小转弯半径或最大转弯末速，系统状态能够收敛至分岔图中目标平衡点位置。同时，适当减小翼伞安装角可以增强伞弹系统对初始角速度扰动的抗干扰能力。