面向结构静力试验监测的高精度数字孪生方法

田阔，孙志勇，李增聪

大连理工大学 工业装备结构分析国家重点实验室 工程力学系，大连 116024

壁板结构大量应用于空间站密封舱、飞机机翼、机身筒段等部件中，起主要承载作用。对壁板结构开展应力场监测，对于保障结构安全性及延长寿命具有重要意义。通过电阻、光纤等传感器可实时监测结构力学响应变化，从而可对危险状况及结构故障进行及时预警［1］以降低结构的维护成本。然而，壁板结构复杂化和大型化的发展趋势，对传感器的监测覆盖度提出了极大的挑战。传感器数量有限，监测信息不全面，无法实现全场的结构应力监测。当一些关键区域的传感器部署位置不正确时，结构应力监测系统甚至会失去作用［2］。尽管采用有限元分析等数值仿真方法可以得到结构的应力场，但建模和分析过程中对物理实体的理想化假设和简化处理，使得仿真结果精度较低［3］，难以准确模拟结构真实的应力变化。因此，为了实现壁板结构全场应力监测，需要综合利用试验和仿真两种强度评估方法的优势，并进行多源数据融合。

近年来，数字孪生技术在智能制造［4］、飞机健康监测［5］、工程优化［6］等领域展现出了应用潜力。在Tao等［7］的综述论文中，多源数据融合被认为是数字孪生研究的关键技术［8］。Wang等［9］通过移动最小二乘法来融合仿真数据和传感器数据，提出了数字孪生建模框架。Xia等［10］基于迁移学习和数字孪生建模技术，将实测故障状态数据与仿真数据融合，建立了机械智能故障诊断框架。董雷霆等［11］提出了包含传感器、物理模型和数据模型的多源异构数据融合方法。综上可见，基于数据融合方法建立数字孪生模型，能够充分发挥试验验证和数值仿真两种强度评估方法的优势，以准确地描述物理实体的状态变化，可为实现结构应力场高精度监测提供潜在的技术手段。

与数字孪生中的多源数据融合技术具有相似的思路和功能，变保真度（Variable-Fidelity，VF）模型通过综合高保真度（High-Fidelity，HF）模型高精度优势和低保真度（Low-Fidelity，LF）模型低成本优势，将两类模型数据进行融合［12］，可以获得高精度的数据融合模型。Tian等［13］采用结构细节完整的精细模型作为HF 模型，等效模型作为LF 模型，基于迁移学习构建的VF 模型显著降低了结构承载分析的计算成本。基于迁移学习和深度神经网络（Deep Neural Networks，DNN）模型，Li等［14］建立了VF 模型，进一步提高了预测精度。Ghosh等［15］把变保真高斯过程模型加入到随机森林框架中，在有限HF 数据条件下，实现了VF 模型建立。然而，上述工作大多是在仿真数据层面上构建不同的VF模型，HF 模型和LF 模型的选择也主要是不同建模精细度的仿真模型。为了将VF 模型推广应用至结构静力试验数字孪生模型建立，可将试验数据作为HF 数据，仿真数据作为LF 数据，进而对两类数据进行融合。

考虑到仿真数据与试验数据样本量的巨大差异［16］，为了构建高精度的结构静力试验数字孪生模型，多源数据融合还需要突破以下两方面挑战。一方面，仿真数据量巨大，模型训练耗时长，导致训练成本无法承受［17］，同时由于仿真分析过程中的离散化、物理模型的简化、求解算法等可能会带来数值噪声［18］，降低模型精度。另一方面，与仿真数据相比，试验数据数量过少，易造成模型训练过度拟合［19］。此外，较少的训练数据可能会增强模型对超参数变化的敏感性造成模型预测结果不稳定。因此，本文的主要目的是建立适用于大样本仿真数据和小样本试验数据的数据融合方法，获得高精度数字孪生模型，实现结构应力场的实时监测。

本文的内容安排如下。第1 节主要介绍面向结构静力试验监测的高精度数字孪生方法，第2节开展开口矩形壁板轴向拉伸试验研究，对比同类数据融合方法，验证所提出方法的有效性，第3节为结论。

1 模型建立与训练

提出面向结构静力试验监测的数字孪生（Digital Twin for Structural Static Test Monitoring，DT-SSTM）方法。

1.1 基于梯度提升树算法的预训练模型

梯度提升树（Gradient Boosting Decision Tree，GBDT）模型［20］是一种以决策树为基学习器的集成学习算法，通过组合多个决策树来提高模型的预测精度和泛化能力。GBDT 算法能够自动处理大样本数据，训练耗时短，并且可以适应不同的数据类型和结构。针对大样本数据，采用合适的超参数可以建立泛化性能较好的GBDT 模型。模型的超参数主要包括决策树数量、决策树深度、学习率和最小样本数。采用GBDT 算法对包含机理信息的大样本仿真数据（LF 数据）建立预训练模型，主要步骤如下：

1）结构数值仿真分析

首先，基于数值仿真方法（如有限元分析），计算结构的力学响应。结构坐标及其力学响应作为原始数据集［X Y Z R］，其中X、Y、Z 为［0，1］中坐标值的归一化值，R 为响应值。

2）网格搜索与交叉验证

网格搜索与交叉验证方法［21］是一种通过给定超参数空间来搜索最佳超参数的优化方法，以获取最佳的超参数。在网格搜索中，采用交叉验证的方式在超参数空间中进行穷举搜索。数据集多次被划分为训练集和验证集，每次将不同的子集作为验证集，其余部分作为训练集。然后对这些子集上的性能评估结果进行对比，选择出最佳的超参数，以提高模型的泛化性能，避免由于模型选择不当导致的过度拟合和欠拟合问题。采用上述方法进行最佳超参数的搜索。

3）建立预训练GBDT 模型

基于网格搜索与交叉验证方法得到GBDT模型的最佳超参数。然后以原始数据集中的坐标值X、Y、Z 为输入，以响应值R 为输出，进行GBDT 模型训练，训练结束可得到预训练GBDT模型。

1.2 基于Stacking 算法的残差模型训练方法

Stacking 算法［22］是集成学习［23］中一种代表性方法，其目的是通过组合多个不稳定的基学习器来增强模型的泛化能力。Stacking 模型通常包括两层结构，第1 层结构为由多个基学习器构建的一级学习器，第2 层结构为由单个基学习器构建的二级学习器。其中一级学习器将数据集进行训练和预测，然后将一级学习器的输出作为输入，经过二级学习器进行最终的预测。当只有少量可用的训练样本点时，Stacking 算法可以降低方差与偏差，相比单一模型预测具有更高预测精度。

支持向量回归（Support Vector Regression，SVR）模型是一种基于统计学习理论的非线性回归模型［24］。其目标是通过在训练数据中找到一个最优的超平面来尽可能减少预测误差，并使用核函数将数据从低维空间映射到高维空间进行非线性建模，从而增加了预测模型的泛化能力，使得SVR 模型在小样本数据中表现良好。并且SVR 模型所需的超参数数量较少，参数调节较简单。

基于Stacking 算法训练以SVR 模型为基学习器的残差模型，目的是在小样本试验数据的情况下，通过集成学习降低残差模型误差，提高模型的稳定性和预测精度。所提出的训练方法示意图如图1 所示，训练过程包括如下步骤：

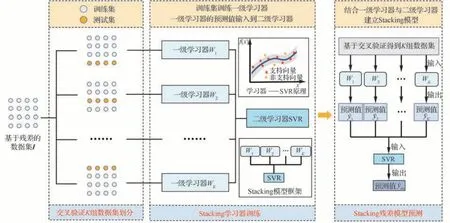
图1 基于Stacking 算法的残差模型训练过程示意图Fig.1 Schematic diagram of residual model training process by Stacking algorithm

1）K 折交叉验证方法

基于新的数据集I，采用K 折交叉验证方法将数据集划分为K 组相同大小的数据集D1，D2，…，DK。设DK+i-1为在第i 次执行时的测试集，剩余的K-1 组数据集为训练集。

2）模型训练

在第i 次交叉验证执行时，通过训练集对SVR 模型训练得到基学习器Wi。基于训练得到的基学习器Wi，通过测试集得到新的预测集Si。经过K 次交叉验证划分后，得到新的预测集S={S1，S2，…，SK}，且生成的新的预测集S 为新数据集I 的响应值R 的预测值。将所得的K 个基学习器W1，W2，…，WK模型作为Stacking 模型的一级学习器。之后，采用新的SVR 模型作为Stacking模型的二级学习器。并将得到的数据集S和R 分别作为训练集的输入值和响应值，对二级学习器进行训练，完成S 到R 的映射。由于Stacking模型中的一级学习器都是单独训练的，因此可以采用并行计算来提高计算效率。

3）模型组合

最后，将得到的K 个一级学习器进行组合。对于未知样本点x，其预测值可表示为

1.3 DT-SSTM 方法的实施步骤

通过对1.1 节和1.2 节的方法进行集成建立DT-SSTM 方法，其总体框架及实施步骤如图2所示，分为离线和在线2 个阶段。

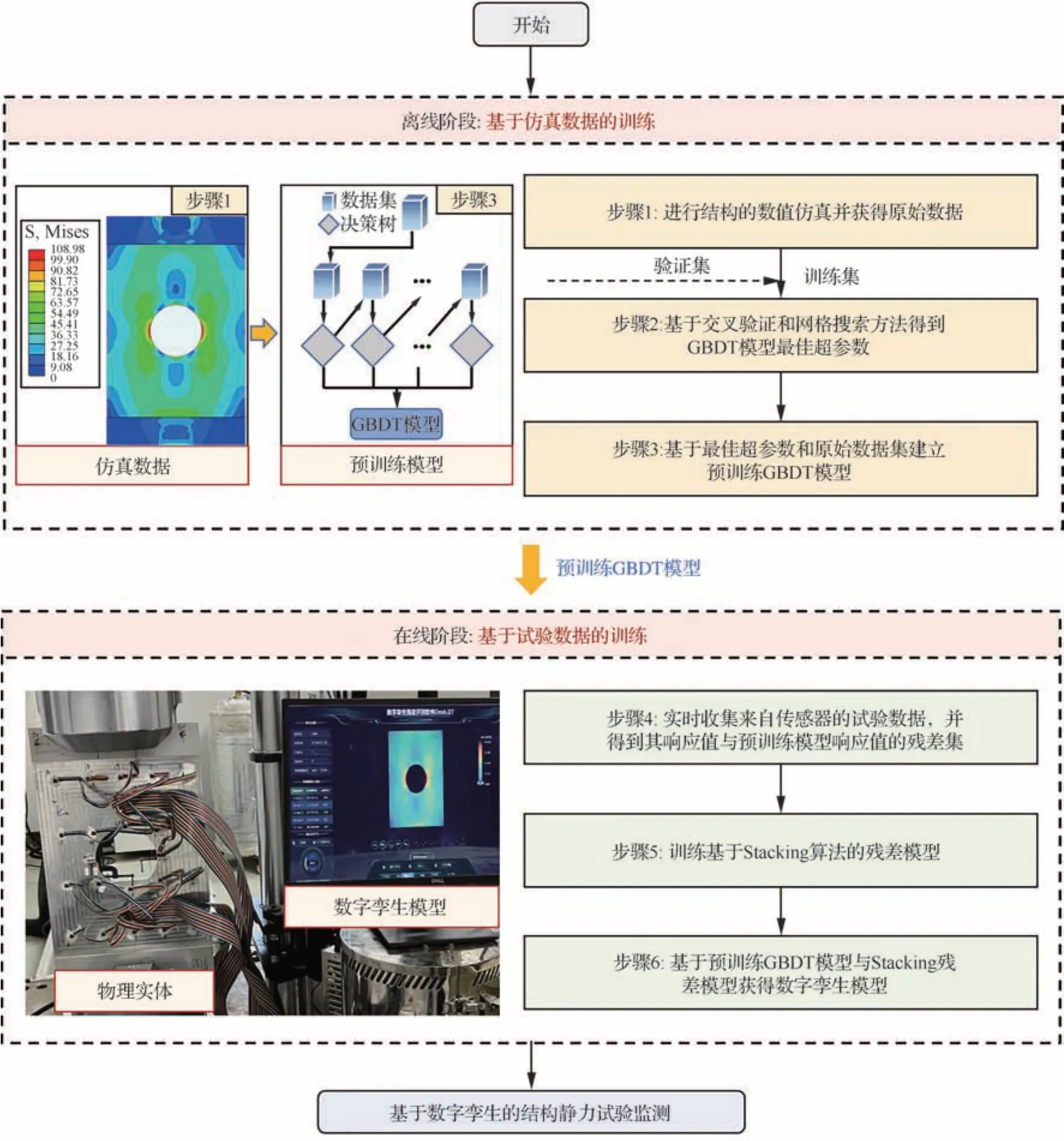
图2 DT-SSTM 方法流程图Fig.2 Flow chart of DT-SSTM method

1）离线阶段：基于仿真数据的预训练模型

离线阶段包括步骤1 到步骤3，其目的是基于大样本有限元仿真数据建立预训练GBDT 模型，该阶段通常在试验前完成。

步骤1：根据实际加载条件和材料属性，基于有限元分析方法对结构进行数值仿真，得到结构的力学响应。将仿真结果作为原始数据集。

步骤2：根据1.1 节介绍的网格搜索和交叉验证方法，将原始数据集划分为训练集和验证集进行GBDT 模型超参数搜索，找出最佳超参数。

步骤3：根据步骤2 得到的最佳超参数，基于GBDT 算法对原始数据集进行训练，建立具有较好泛化性和精度的预训练GBDT 模型。

2）在线阶段：基于试验数据的残差模型

在线阶段包括步骤4～步骤6，对实时获得的试验数据训练Stacking 残差模型。通过结合预训练GBDT 模型与残差模型，建立多源数据融合的数字孪生模型。

步骤4：实时采集由预先布置在结构上的传感器获得的试验数据。建立归一化后的传感器坐标集［X1Y1Z1］、传感器数据响应值和对应的预训练模型预测值之间的残差集H，进而建立新的数据集I1=［X1Y1Z1H］。

步骤5：基于第1.2 节所提出的方法，通过K折交叉验证将数据集I1划分为训练集与测试集，基于训练集对SVR 模型训练，得到K 个基学习器，并将其作为一级学习器。之后将基于测试集得到的一级学习器的预测值作为输入值，残差集H 作为响应值对新的SVR 模型进行训练，得到二级学习器，将一级学习器与二级学习器结合，完成Stacking 残差模型的训练。基于残差模型的训练，可建立传感器坐标集［X1Y1Z1］与残差集H的映射关系［25-26］。由于仿真数据和传感器数据坐标值处于同一坐标空间中。因此，基于已有的映射关系，可将结构全场的坐标值输入到残差模型，得到全场的残差值。

步骤6：结合预训练GBDT 模型与Stacking残差模型，建立多源数据融合模型，所构建的多源数据融合模型可表示为

式中：yGBDT(x)表示基于GBDT 算法的预训练模型；δStacking(x)表示基于Stacking 算法的残差模型；yMSDF表示多源数据融合的数字孪生模型。

基于多源数据融合模型，建立面向结构静力试验监测的数字孪生模型，实现结构应力场监测和强度评估。

在建立结构静力试验数字孪生模型后，使用模型评 价指标［27］来评估DT-SSTM 方法的 预测能力。采用相对均方根误差（Relative Root Mean Square Error，RRMSE）和R2作为数字孪生模型全局预测精度的评价指标：

式中：N代表样本总数；yi表示真实值表示预测值表示真实值的均值。

RRMSE 值越接近0 表示模型精度越高，R2值越接近1 表示模型精度越高。由于RRMSE 值和R2值对于全局预测精度的结果相似，为表述简单起见，主要使用RRMSE 值进行精度评价，而R2值作为参考。在试验研究中，预测和评估当前状态下结构的最大力学响应对于强度评估是非常重要的。因此，结构的局部精度可以通过结构最大试验值与其预测值之间的相对误差来评价，记为REmax，可表示为

式中：y∗代表结构最大试验值代表数字孪生模型相应的预测值。

2 开口矩形壁板轴向拉伸静力试验

通过开展开口矩形壁板轴向拉伸静力试验，验证DT-SSTM 方法的预测精度。为了充分对比说明所提出方法有效性，采用前期研究中建立的基于迁移学习的变保真度代理模型［28］（Transfer Learning-based Variable-Fidelity Surrogate Model，TL-VFSM）以及基于径向基函数的加法标度函数（Additive Scalar Functions by Radial Basis Functions，ASF-RBF）模型［29］和Co-Kriging模型［30］等数据融合方法进行比较。

2.1 开口矩形壁板静力试验数字孪生模型建立

首先，在开展静力试验前，基于有限元分析方法对结构进行数值仿真。如图 3（a）所示，开口矩形壁板的高度为500 mm，宽度为400 mm，厚度为1.8 mm。板上开口直径为150 mm。在板的底部和顶部分别用两块尺寸为400 mm×80 mm×10 mm 的夹块来固定。板的材料为6061 T651 铝合金，弹性模量为69.8 GPa，泊松比为0.33，屈服强度为276 MPa，强度极限为310 MPa，密度为2.7×10-6kg/mm3。如图3（a）所示，用53 363 个简化积分单元（S4R）对结构进行网格划分，用96 480 个8 节点连续体简化积分单元（C3D8R）对两个夹块进行网格划分，网格划分节点总数为169 961个。基于显式动力学方法［31］计算得到如图 3（b）所示的位移载荷曲线。壁板的极限承载力约为35 000 N，为了监测开口矩形壁板在线性阶段的应力变化，试验最大载荷设置为20 000 N。同时，为了保证计算时间的可对比性，本文中所有的计算都在配置为Intel（R）Xeon（R）Gold 6248R CPU@3.00 GHz和512 G RAM 的工作站上进行。

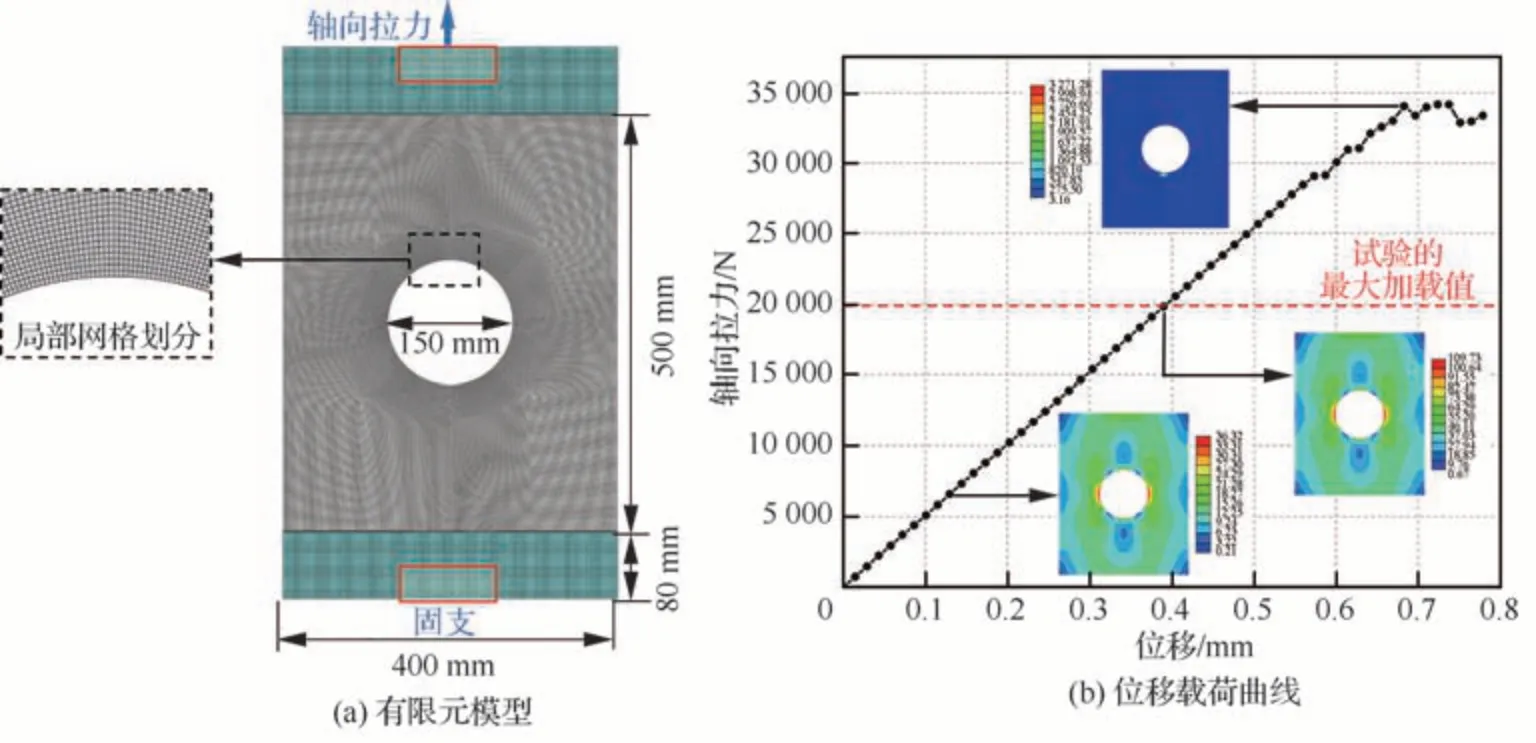
图3 开口矩形壁板的有限元模型及仿真结果Fig.3 FE model and simulation results of open-hole rectangular plate

其次，开展轴向拉伸载荷作用下开口矩形壁板试验。基于万能试验机（型号为SHIMADZU EHF-UV），对壁板进行准静态轴向拉伸。如图 4（a）所示，将传感器（24 个应变花）均匀布置在壁板上。试验测点位置的Mises 应力值由应变花0°、45°以及90°通道测得的应变值进行计算。在本研究中，使用12 个应变花作为训练集，另外12 个应变花作为测试集。同时，采用离开口最近的09 号传感器，即强度最薄弱的区域的试验测量结果与数字孪生预测结果计算REmax，目的是评估数字孪生模型对壁板局部危险区域的预测精度。搭建的结构静力试验数字孪生试验系统如图4（b）所示，包含万能试验机、控制系统、动态应变测量仪、试验件（物理实体）以及与其相互映射的数字孪生模型。

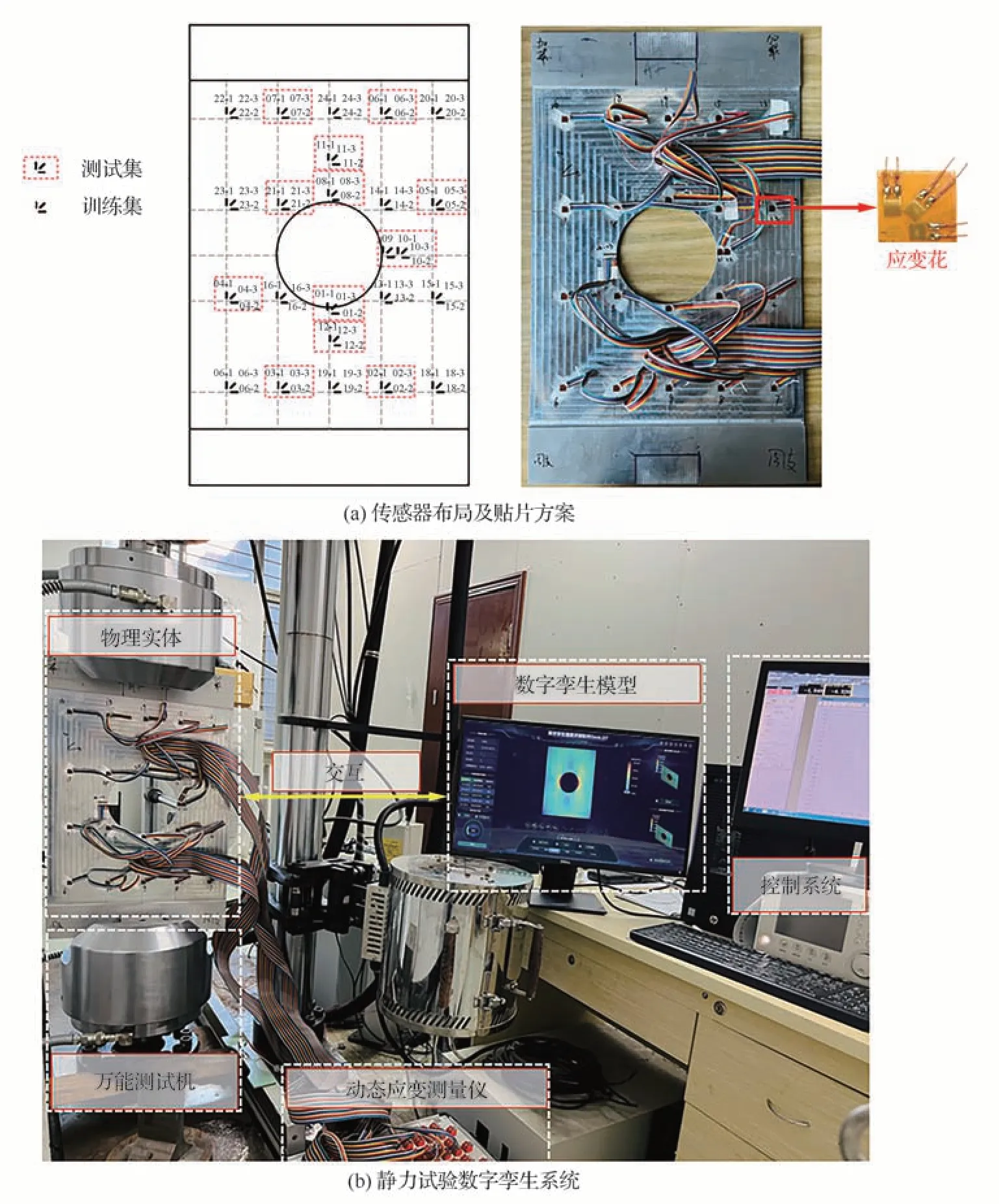
图4 开口矩形壁板静力试验数字孪生系统Fig.4 Static test digital twin system for open-hole rectangular plate

最后，基于离线仿真数据和在线试验传感器数据，通过DT-SSTM 方法开展数据融合以建立数字孪生模型，进而实现壁板结构应力场实时监测和强度评估。

2.2 静力试验数字孪生应力场监测结果与讨论

对比和讨论各方法对开口矩形壁板应力结果的全局和局部预测精度。基于已得到的开口矩形壁板在加载20 000 N 时的仿真数据和试验数据，采用有限元分析、径向基函数（Radial Basis Functions，RBF）、GBDT、Co-Kriging、ASFRBF、TL-VFSM、DT-SSTM 方法得到的开口矩形壁板数字孪生应力场监测精度如表1 所示。各方法得到的壁板应力场分布结果如图5 所示。

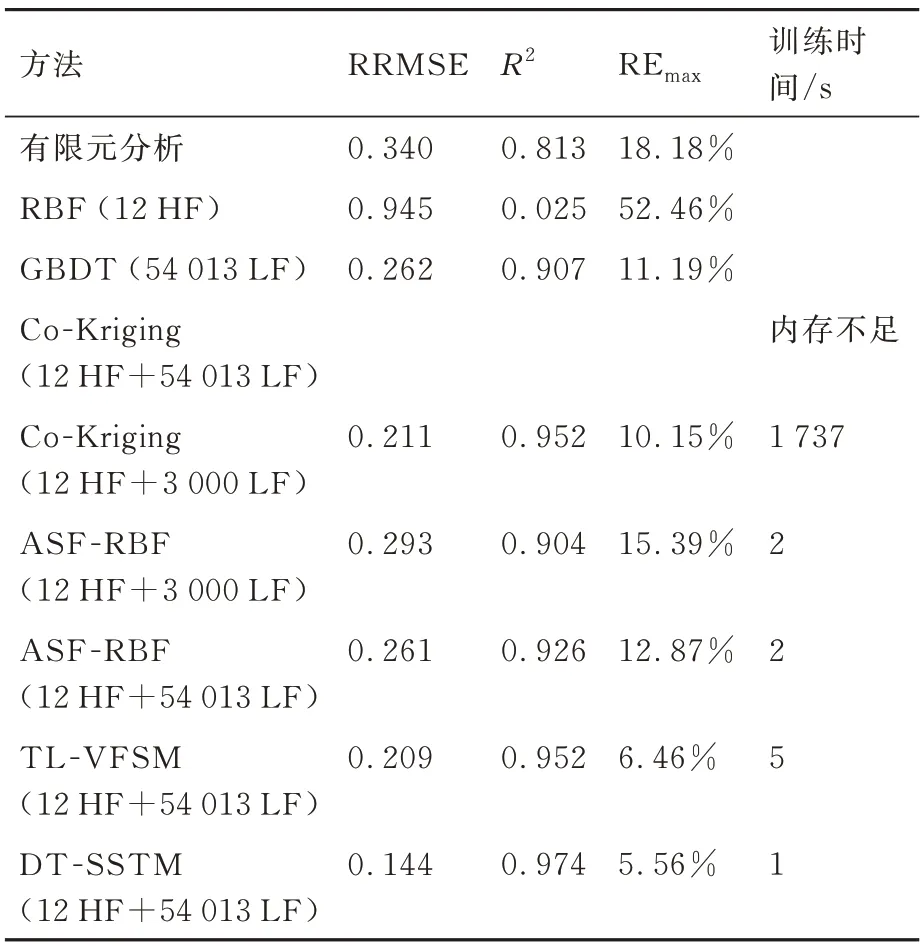
表1 各方法预测精度和训练时间（20 000 N 轴向拉力）Table 1 Prediction accuracy and training time of different methods（Axial tension load of 20 000 N）

图5 各方法得到的开口矩形壁板应力场预测结果（20 000 N 轴向拉力）Fig.5 Stress field prediction results of open-hole rectangular plate by different methods（Axial tension load of 20 000 N）

首先，有限元分析应力场分布结果如图5（a）所示，预测结果RRMSE 值为0.813，REmax值为18.18%，说明其预测结果的全局和局部精度较低。基于12 个HF 样本点构建的RBF 代理模型精度也较低（RRMSE=0.945，REmax=52.46%），这主要是由于HF 样本点数量不足导致，其应力场分布结果如图5（b）所示。因此，仅依靠HF 数据或LF 数据构建的模型预测精度较低，难以高精度地监测结构应力场变化。

进而，基于DT-SSTM、Co-Kriging、ASFRBF和TL-VFSM 方法，分别针对轴向拉力为20 000 N时的53 363 个LF 样本点和12 个HF 样本点进行数据融合，各方法的预测精度如表 1 所示。由于LF 样本点数量较大，Co-Kriging 方法会出现内存不足、无法训练的问题，因此随机采样3 000 个LF 样本点进行训练。相比之下，DTSSTM 方法中的GBDT 算法可以有效处理仿真数据量庞大以及存在噪声值等问题。基于网格搜索和交叉验证方法得到GBDT 模型的最佳超参数，进而通过训练原始数据集得到预训练模型。GBDT 模型的超参数设置为决策树数量为200，最大深度为8，学习率为0.03，最小样本数为2。与有限元分析结果相比，GBDT 方法具有更高的预 测精度（RRMSE=0.262，REmax=11.19%），验证了GBDT 算法能够建立泛化性较好、精度较高的预训练模型。

从表1 对比可以看出，DT-SSTM 方法的RRMSE 值比ASF-RBF 方法减小了44.83%，比Co-Kriging 方法减小了31.75%，比TL-VFSM方法减小了31.10%。同样，DT-SSTM 方法的REmax值比ASF-RBF 方法降低了56.80%，比Co-Kriging 方法降低了45.22%，比TL-VFSM方法降低了13.93%。精度结果表明，DT-SSTM方法具有较高的全局和局部精度，只需少量传感器即可准确监测结构应力场。同时，在表2 给出了不同传感器测点下各方法的Mises 应力预测结果。同时基于测试集的试验数据、仿真数据和所提出方法的Mises 应力结果如图6 所示。

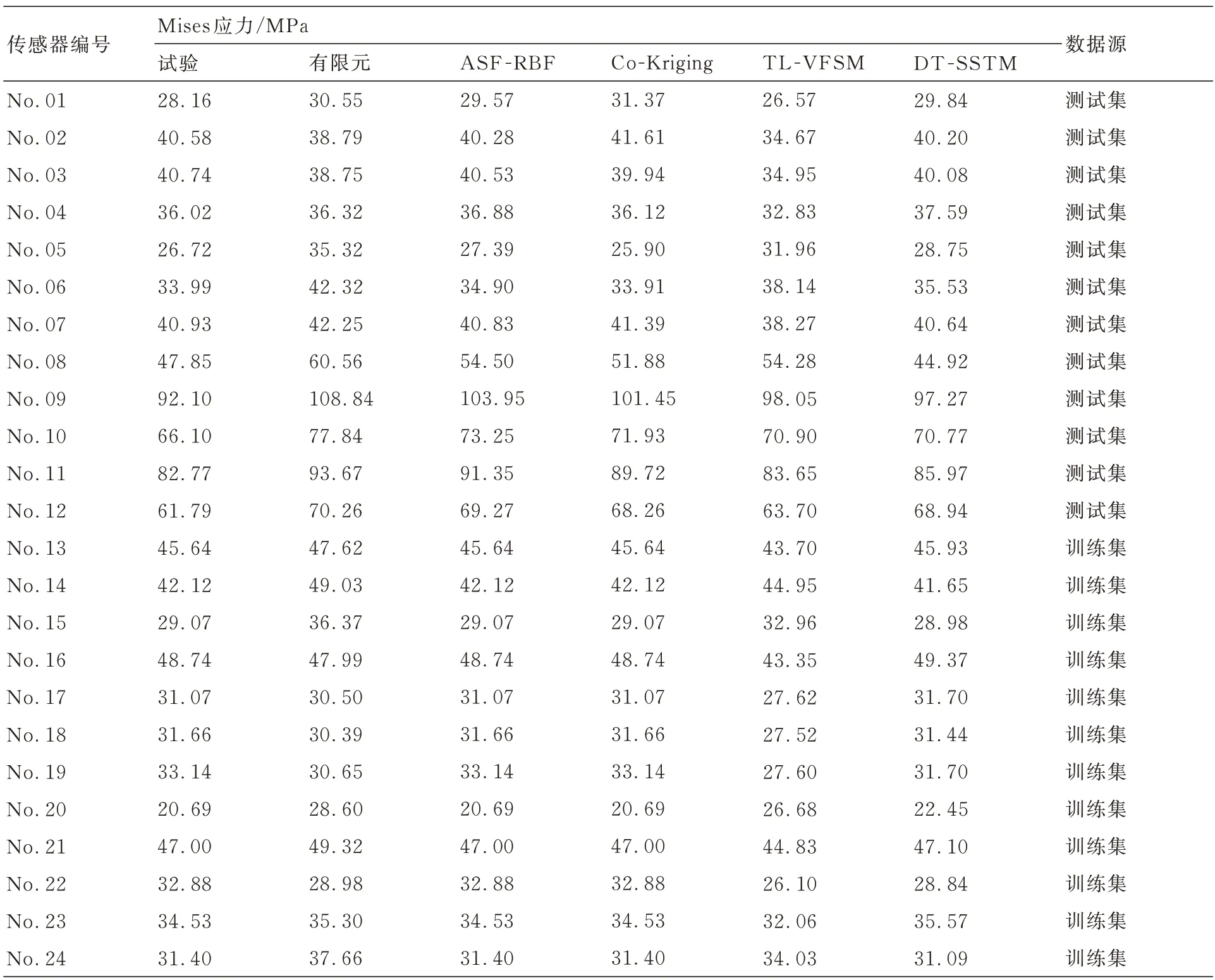
表2 不同传感器测点下各方法的Mises 应力结果Table 2 Mises stress results for various methods with different sensor measurement points

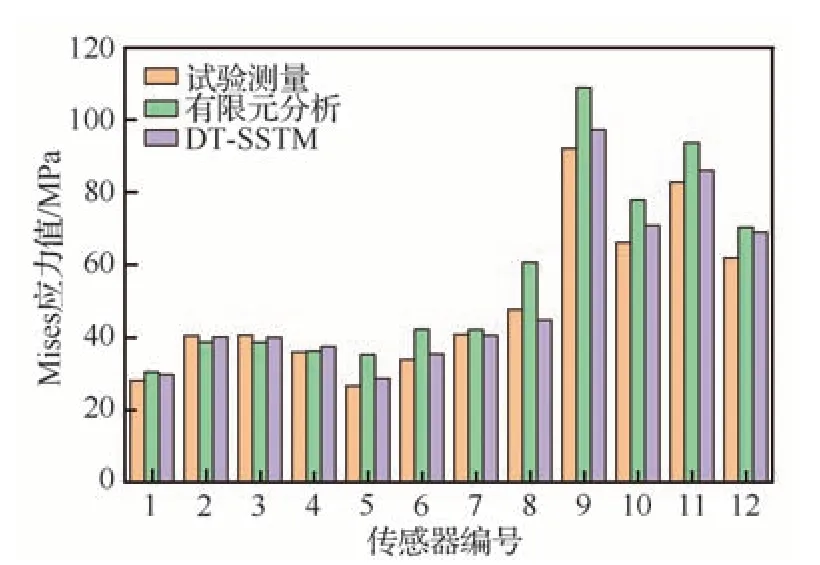
图6 不同传感器测点（测试集）下各方法的Mises 应力值Fig.6 Mises stress values for different methods with different sensor measurement points（Testing set）

同时，为了验证所提出方法的融合效率，表1中给出了各方法的训练时间。由于在结构应力场实时监测过程中不考虑离线阶段计算成本，因此仅对在线阶段模型训练时间进行计算。具体来说，训练时间的统计方式是从在线阶段采集到来自传感器的试验数据开始，一直到完成数字孪生模型建立所花费的时间。由表1 可知，DTSSTM 方法的训练时间较ASF-RBF、Co-Kriging和TL-VFSM 3 种数据融合方法减少了50%以上，具有更高的融合效率，保证了数字孪生模型实时性。

为了验证所提方法在不同加载载荷幅值下的适用性，开展了开口矩形壁板在轴向拉力为22 000 N 时应力场预测的算例研究。所提出方法与ASF-RBF、Co-Kriging、TL-VFSM 3 种融合方法针对开口矩形壁板应力场的全局和局部预测精度结果如表3 所示，壁板应力场分布结果如图7 所示。由表3 可见，DT-SSTM 方法的RRMSE 值比ASF-RBF 方法减小了39.58%，比Co-Kriging 方法减小了37.63%，比TL-VFSM方法减小了28.10%。DT-SSTM 方法的REmax值比ASF-RBF 方法降低了30.41%，比Co-Kriging 方法降低了21.53%，比TL-VFSM 方法降低了3.00%。从在线阶段的训练时间也可以看出，提出方法仅需1 s，相比其他3 种方法具有更高效率。综上，所提出方法在不同加载载荷幅值下较其他方法仍具有更高的全局与局部预测精度、更少的训练耗时，验证了所提出方法的适用性。

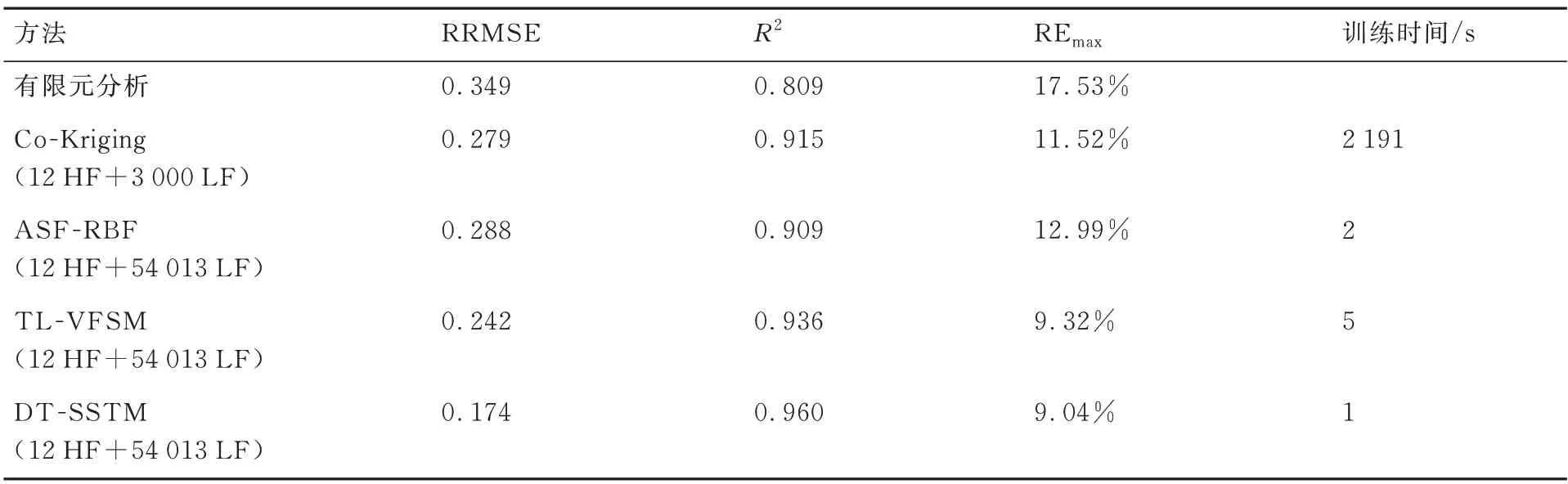
表3 各方法预测精度和训练时间（22 000 N 轴向拉力）Table 3 Prediction accuracy and training time of different methods（Axial tension load of 22 000 N）

图7 各方法得到的开口矩形壁板应力场预测结果（22 000 N 轴向拉力）Fig.7 Stress field prediction results of open-hole rectangular plate by different methods（Axial tension load of 22 000 N）

3 结论

1）提出了一种面向结构静力试验监测的数字孪生（DT-SSTM）方法。基于GBDT 模型和Stacking 模型分别对大样本仿真数据和小样本试验数据进行训练，建立了高精度的结构静力试验数字孪生模型。

2）开展了开口矩形壁板轴向拉伸试验验证，试验结果表明，DT-SSTM 方法比ASF-RBF、Co-Kriging 以及TL-VFSM 3 种经典数据融合方法RRMSE 值分别减小了44.83%、31.75%、31.10%，REmax值分别减小了56.79%、45.22%、13.93%，DT-SSTM 方法具有最高的全局和局部精度，并且可实时准确监测结构的应力场变化，验证了方法的有效性。