基于载荷谱的电池包疲劳试验与计算方法
2024-05-03上官文斌岳炼吕辉周孚鹏
上官文斌 岳炼 吕辉 周孚鹏
(1.华南理工大学 机械与汽车工程学院,广东 广州 510640;2.祥鑫科技股份有限公司,广东 东莞 523870)
电池包作为新能源汽车的重要组成部件,不仅起着储存、传输电能的作用,其安全特性更是直接关乎电动车的安全可靠性。电池包作为“三电”系统的核心部件,大多直接安装在汽车底盘下方,承受来自路面和电机的各种激励。因此,保证电池包具有足够长的疲劳耐久寿命以满足电动车的使用周期,已成为整车研发的重点关注对象[1]。
对于电池包的疲劳寿命预测,相关研究人员基于有限元分析和数值理论提出了相应的计算方法。但是在这类研究当中,大多数分析计算得出的结果,均缺少相应的试验验证,无法证实计算分析方法的可靠性。更为重要的是,研究人员在建立电池包的疲劳寿命分析模型时,仅仅对电池箱体进行了粗略的建模,对电池箱体结构进行了一定的简化,同时电池模组均是用方形质量块[2]或者质量点[3]代替,忽略了电池模组中各零部件的疲劳失效。对于电池包内的连接方式,进行了一定的简化,将焊接和螺栓连接采用刚性连接代替[4],忽略了连接方式的疲劳失效,无法保证仿真分析结果的可靠性。同时,对于电池包的振动试验,相关研究人员花费了大量的精力在探究电芯的振动试验[5-8]或者电芯支架的振动试验[9],提出了针对电芯的振动试验方法,但是无法普及应用到电池包的随机振动试验中。因为电芯体积小、质量轻,很容易保证振动信号的准确传递,但是电池包体积大、质量大,在随机振动试验中,振动信号在传递过程中很容易产生误差。因此在电池包的随机振动试验中,为了确保试验的准确性,保证振动信号的传递非常重要。
本文以电动车电池包为研究对象,研究了电池包随机振动试验方法和疲劳特性的计算方法。首先提出了验证振动信号在振动台、工装夹具、电池包之间传递的方法,给出了电池包结构和功能上的系统性检查方法;然后对电池包进行随机振动试验,并检查出电池包的损伤部位。最后提出了电池包疲劳损伤特性的计算方法,基于电池包精细化模型,采用Goodman疲劳寿命估算方法和Miner线性累积损伤法则,对电池包进行了随机振动疲劳损伤分析。将分析得到的电池包疲劳损伤部位与试验结果进行对比,验证了计算方法的准确性,对后续电池包的疲劳特性的研究有一定的参考作用。
1 电池包疲劳试验
在对电池包进行随机振动试验前,需对振动信号传递路径进行检查,确保振动台发出的信号传递到电池包与工装的连接处。试验后需对电池包进行结构与功能性检查,以确认电池包是否在随机振动过程中发生损坏。
1.1 疲劳试验的载荷
在随机振动试验中,输入的载荷谱要和电池包在实车运行中所受到的载荷一致。为得到符合实际行车工况中电池包的输入功率谱密度,本文通过对电动汽车在各典型工况行驶时采集并处理得到电池包与车身连接处的功率谱密度,用以模拟电池包在实车运行中所受到的载荷。
在城市道路、乡村公路、高速路和坏路等典型道路条件下,在电池包与车身连接处布置加速度传感器,通过实车路谱采集试验,得到了车辆运行过程中电池包与车身连接部位的加速度信号。随后基于等损伤原则,计算得到电池包随机振动试验所需的功率谱密度曲线[10],如图1所示。动力电池需满足使用年限达到5~8年或行驶十万公里的设计要求,依据等损伤原则,为模拟电池包在使用年限期间所受到的随机振动造成的损伤,要求各个方向振动时间不低于48 h。

图1 电池包随机振动功率谱密度曲线Fig.1 Random vibration power spectral density curve of battery package
1.2 振动试验方法
振动试验流程如下:选取3个同样的电池包作为样包用于随机振动预实验,命名为A号、B号、C号,分别在3台振动台上同时进行X,Y,Z方向上的随机振动,验证系统工作是否正常并且探究电池包在单方向振动中的损伤状况。本章以X向随机振动为例对试验方法进行介绍。
1.2.1 振动加速度的频响特性
将加速度传感器均匀地布置在台面、夹具和电池包上,通过对比传感器测量示数与输入加速度值,即可验证振动信号的传递。各个加速度传感器的编号和安装位置如图2所示。

图2 传感器布置位置Fig.2 Sensors location
(1)振动台台面加速度
为确保输入的振动信号传递至振动台,对振动试验台进行空载扫频试验,扫频范围选取为5~250 Hz。同时,为了尽可能的减少扫频对夹具和电池包的损害,在能够顺利进行扫频试验的前提下,扫频加速度则需要越小越好,因此选取振动系统的最小稳定振动加速度a=0.5g。设定扫频停机上下线与警告上下线,图3中分别用红色实线与黄色虚线表示。若加速度曲线超过警告上线且出现明显峰值,则结构出现共振,峰值所对应的频率为结构的共振频率。因此规定扫频得到的加速度曲线应在加速度警告线内,以确保振动信号传递至振动台。

图3 振动台台面加速度频率响应特性曲线Fig.3 Acceleration frequency response curves of shaker table
图3为振动台X方向扫频结果。由图可见,振动台台面X向的加速度频响曲线均在规定范围内,表明输入信号能够准确地传递至振动台台面。
(2)工装空载端板处的振动加速度
对工装进行空载扫频试验,测量得到工装空载端板处加速度频响特性曲线如图4所示。

图4 工装空载端板处加速度频响特性曲线Fig.4 Acceleration frequency response curves at the no-load end plate of the fixture
由图4可见,在高频范围内(大于150 Hz),工装夹具振动加速度值出现较大波动,这是因为工装夹具并不是一个完全刚性的体系。但在电池包随机振动的规定频率范围内(5~150 Hz),测得的加速度均在规定范围内,该工装夹具符合试验要求。
(3)工装端板及电池包上振动加速度
将电池包安装至工装上,对电池包进行扫频试验,图5为电池包X方向扫频结果。

图5 X向电池包扫频结果Fig.5 Frequency sweep results in X axis
由图5(a)可见,在5~150 Hz频率范围内,电池包与工装连接端板处传感器测量得到的振动加速度值均位于规定范围内,表明振动信号准确地传递至电池包。同时由图5(b)可得电池包共振频率,用作后续对比。
1.2.2 电池包随机振动
在完成以上振动信号的检查之后,对电池包进行随机振动试验。输入随机振动功率谱密度参数,以X向随机振动试验为例,图6为随机振动中工装与电池包连接平台上传感器测得的功率谱密度曲线。由图6可得,电池包随机振动试验时,工装与电池包连接平台上的振动信号与振动台面输入功率谱密度曲线变化趋势一致,进一步证实了振动信号能够较为准确地传递至电池包。

图6 电池包X向随机振动功率谱密度曲线Fig.6 X axis random vibration PSD curves of battery package
在A号和B号电池包的随机振动试验完成后,读取BMS监测设备监测参数,电芯各性能参数无明显改变,证实了电池包试验前后功能无损坏。
C号电池包在Z方向随机振动过程中突然出现异响,为防止电池包出现进一步的损坏而引发火灾或爆炸等危害,及时停止试验,等待进一步的检查。
1.3 电池包随机振动结果分析
1.3.1 电池包共振频率分析
随机振动试验结束后,对完成随机振动测试的A号电池包和B号电池包进行共振频率分析。振动前后电池包共振频率对比如表1、表2所示。
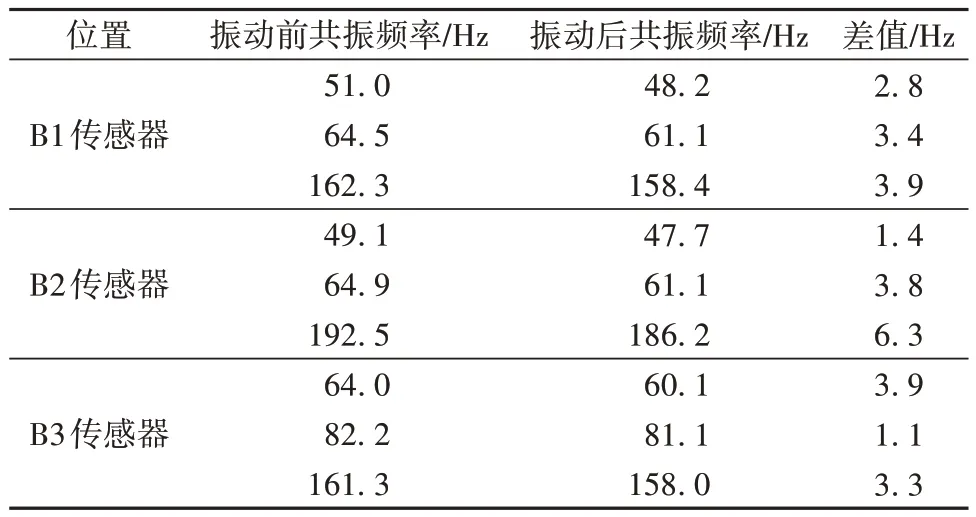
表1 X向振动前后电池包共振频率对比Table 1 Comparison of battery package resonance frequencies before and after X axis vibration

表2 Y向振动前后电池包共振频率对比Table 2 Comparison of battery package resonance frequencies before and after Y axis vibration
由表1和表2可知,电池包随机振动前后共振频率相差均小于10 Hz,因此判定电池包X和Y向随机振动对电池包结构无明显损坏。
1.3.2 电池包性能检查
为进一步检查电池包性能,对随机振动后的电池包进行各项性能检查,检查结果为:
(1)A号和B号电池包压降分别为22.9和20.4 Pa,绝缘电阻均为10 MΩ/V。各项性能仍能满足设计要求,电池包安全地通过随机振动试验。
(2)C号电池包压降为121 Pa,超过100 Pa,断定为电池包气密性失效,电池包结构在随机振动中发生损坏。对C号电池包进行更全面的拆包检查,检查得出C号电池包损伤位置如图7所示。

图7 C号电池包损伤部位检查Fig.7 Inspection for damaged parts of battery package C
对C号电池包损伤部位进行分析得出,前3处损伤均是由于结构强度不足导致的振动开裂,而最后一处托架与右侧挂载点盖板处开裂,是由于此处焊点工艺制造误差导致虚焊,存在一定的偶然性。
2 电池包振动疲劳的计算与分析
2.1 电池包有限元模型的建立
有限元模型是疲劳分析的基础和关键,为模拟电池包在振动工况中力的真实传递路径,需要对电池包建立精细的有限元模型。
2.1.1 电池箱有限元模型
本文以电动汽车所装配的电池包为研究对象,为尽可能的还原电池包内部各结构,对电池箱体进行了精细化建模,如图8所示。
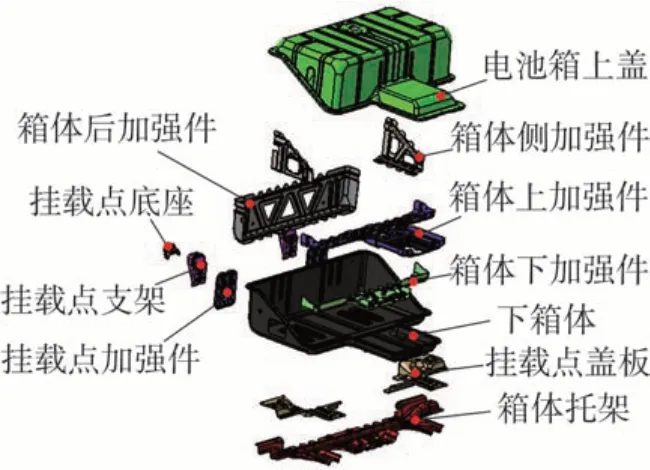
图8 电池箱模型Fig.8 Battery package model
将三维模型导入HyperMesh有限元软件中,进行有限元网格划分。电池箱各零部件均为钢板冲压件,厚度均在3 mm之内,为保证计算精度并减少网格数量,各零部件均采用壳单元进行网格划分。
2.1.2 模组有限元模型
模组作为电池包的主要零部件,其质量占据了整包质量的80%,本文为了更准确地模拟模组内部以及模组与电池箱之间力的传递路径,以电芯为最小单元,对模组进行了精细化建模,如图9所示。

图9 模组三维模型Fig.9 Module digital model
将模组模型进行有限元网格划分,不考虑电芯在振动工况中的失效,在分析中将电芯材料定义为可压缩泡沫[11],仅考虑电芯重量。电芯中的钣金件均采用壳单元进行网格划分,其余实体为保证网格质量,采用六面体网格划分。
2.1.3 连接方式有限元模型
在电池包有限元模型中,为准确地模拟出电池箱内各零部件之间力的传递路径,需对电池箱体内各零部件的连接方式进行精细化建模。
在冲压电池箱体中,焊接作为主要的连接方式,且作为振动中较易失效的连接方式,必须在疲劳损伤分析中进行精确地模拟[12]。
不同的仿真分析模型所选择的焊接建模方法各有不同。本文为精确地模拟出电池包中各零部件之间力的传递路径,需在模型中精确地模拟出焊点、焊缝的位置和受力状况,同时由于该电池包内焊点、焊缝数量众多,对每个焊点、焊缝及其连接部件进行局部细化网格的话,网格数量太多、计算量大。因此本文所研究的电池包内的焊点均采用ACM2单元模拟,该焊点单元是由六面体单元模拟焊核,通过RBE3单元连接六面体单元和焊接面;焊缝均采用棱柱单元模拟,该焊缝单元是由棱柱单元模拟焊缝,通过RBE3单元连接棱柱单元和焊接面。
对于螺栓连接,在电池包内主要用于连接上盖与箱体、模组与箱体,力的传递形式相对简单,并且螺栓强度大而承受的力和力矩较小,因此为了减少分析计算时间,在本研究中不考虑螺栓的失效,采用RBE3单元和梁单元进行模拟。
2.2 疲劳寿命分析方法
对于本文所研究的电池包在随机振动工况中,电池包各零部件的疲劳特性均属于高周疲劳问题,因此本文采用适用于计算高周疲劳问题的名义应力法。
名义应力法(S-N法)作为最早的疲劳寿命预测方法,以材料疲劳特性参数曲线为基础,以结构所受对称循环等效应力为参数进行疲劳寿命的预测。因此,需将结构在实际工况中所受的实际应力转换为对称循环等效应力,消除平均应力对疲劳寿命的影响[13]。针对对称循环等效应力的计算方法,本文为了保证计算结果的可靠性,采用计算相对较为保守的Goodman方法。
而振动疲劳破坏是由每次振动产生的损伤累积造成的,当损伤累积超过某一临界值之后,结构便会发生疲劳破坏[14]。本文采用所需材料参数较少,形式简洁且计算精度较高的Miner线性累积损伤法则对电池包疲劳损伤进行计算。
2.3 电池包振动疲劳分析
对电池包进行随机振动疲劳分析,分析电池包可能出现的损伤部位与电池包随机振动试验形成对照,验证电池包疲劳分析模型的准确性。
2.3.1 频率响应分析
采用模态叠加法对电池包进行频率响应分析,将电池包有限元模型导入Abaqus有限元分析软件中,对电池包进行约束模态分析,得出电池包1~150 Hz范围内的所有模态。
得到电池包模态频率后,对电池包分别施加X、Y、Z方向上的单位加速度g(9.81 m/s2)载荷,进行5~150 Hz的扫频分析,分别得到电池包在3个方向上的频率响应,作为疲劳分析的关键输入。
2.3.2 电池包疲劳寿命计算
本文采用nCode Designlife疲劳仿真软件,该软件可以通过材料的屈服极限、抗拉极限和弹性模量等参数对材料S-N曲线进行近似估算。
以X向随机振动疲劳响应分析为例,将电池包的频率响应分析结果导入疲劳分析软件中,定义电池包材料参数,同时导入X向随机振动功率谱密度曲线。将振动循环时间定义为48 h。使用Miner线性累积损伤法则,采用Goodman方法对平均应力进行修正,以消除平均应力对疲劳寿命的影响。
电池包的X向随机振动疲劳损伤结果如图10(a)所示。由图可见,电池包最大损伤位置位于上盖前部凸起与后部过渡处,最大损伤值为0.29,小于1(1表示经历完整循环次数的随机振动后零件刚好损坏),表明电池包在X向的随机振动中无结构件损坏。

图10 随机振动疲劳损伤云图Fig.10 Random vibration fatigue damage nephogram
Y、Z方向电池包随机振动疲劳响应分析步骤与X向类似,不再赘述。电池包Y向随机振动疲劳损伤结果如图10(b)所示。由图可见,电池包最大损伤位置位于上盖后端左右角螺栓孔处,最大损伤值为6.09×10-4,远小于1,表明电池包在Y向随机振动中无结构件损坏。
电池包Z向随机振动疲劳损伤计算结果如图10(c)、10(d)所示。由图可见,电池包最大疲劳损伤值大于1,分别位于上盖前部凸起与后部过渡处(最大损伤值为2.78)、箱体与后挂载点搭接处(最大损伤值为1.27)、箱体与托架搭接处(最大损伤值为4.26),表明在Z向随机振动过程中,电池包这3处位置出现疲劳损伤。
将电池包随机振动试验结果与有限元疲劳分析结果进行对比,如表3所示。由表3可知,X方向和Y方向电池包随机振动疲劳分析结果与试验结果一致,均为安全通过随机振动试验,电池包无损坏。Z方向电池包随机振动试验得到前3处损伤部位与分析得到的失效部位基本一致,但是最后一处(托架与右挂载盖板处)分析与试验结果出现差异。而在电池包随机振动试验时,对电池包进行拆包检查时便已经得出,最后一处损伤为工艺制造误差导致,存在偶然性。

表3 电池包疲劳分析与试验结果对比Table 3 Comparison of analysis and test results of battery packages
综上所述,基于本文提出的电池包疲劳损伤计算方法,对电池包随机振动疲劳损伤部位进行预测,预测得到的损伤部位与试验损伤部位具有较好的一致性,验证了计算方法的准确性。
3 结论
(1)建立了电池包随机振动的测试方法,最大限度的规避了试验台、夹具、电池包之间振动信号传递的误差,保证了测试结果的准确性。同时还对电池包进行了结构和功能上的系统性检查,确保了电池包检查结果的全面性与可靠性。
(2)提出了电池包精细化建模方法,分别对电池箱、电池模组、电池包内各连接方式进行了精细化建模,保证了分析模型的完整性,进一步保证了分析结果的可靠性。
(3)基于电池包精细化模型,提出了电池包疲劳特性计算方法,对电池包进行随机振动疲劳损伤分析。结果表明:仿真分析得到损伤部位与试验得到的实际损伤部位具有较好的一致性,证实了计算方法的准确性与可靠性。
