基于水平集带方法的柔顺机构拓扑优化研究

魏鹏 何磊 许伟鹏 陈起 刘杰 龙凯

（1.华南理工大学 土木与交通学院/亚热带建筑与城市科学全国重点实验室，广东 广州 510640；2.广东技术师范大学机电学院，广东 广州 510665；3.燕山大学 机械工程学院，河北 秦皇岛 066004；4.华北电力大学 新能源电力系统国家重点实验室，北京 102206）

机构是一种能够传递力、运动或能量的机械装置。不同于传统机构的刚体运动工作方式，柔顺机构通过自身的弹性变形实现力与运动的传递［1］。凭借着在降低成本和提高性能等方面的显著优势，柔顺机构在微创手术、空间机器人以及微型机电系统（MEMS）领域得到了广泛的研究和应用。

拓扑优化是设计柔顺机构的有效手段，当前主流的拓扑优化方法包括变密度法［2］、渐进结构优化法［3］以及水平集法［4-5］等。不同于需要先确定基本构型的伪刚体模型设计方法，拓扑优化方法在仅已知设计域、边界条件、输入和输出条件的前提下，就可综合设计出大量不同形式的功能型柔顺机构［6］。同时，柔顺机构分析的非伴随特性也使其成为考验优化方法的经典算例。

在方法应用层面，变密度法在柔顺机构设计中的发展历史最为久远。1994年，Ananthasuresh等［7］首次将拓扑优化方法应用在柔顺机构的设计中，证实了拓扑优化技术可以成为多功能柔顺机构设计的有力工具。1997年，Sigmund［8］基于固体各向同性材料惩罚模型（SIMP模型），以几何增益等作为目标函数研究了柔顺机构的优化设计问题。李兆坤等［9］基于变密度法提出了一种考虑可靠度的几何非线性柔顺机构设计方法。张宪民等［10］基于SIMP模型和并行求解策略，提出了一种多材料热固耦合柔顺机构的设计方法。

此外，水平集方法凭借其在处理复杂拓扑演化以及提供清晰结构边界等方面的优势，也逐渐成为柔顺机构优化设计的重要方法［11］。水平集方法首先由Osher等［4］提出，用于描述曲面或曲线的演化过程，后由Sethian等［5］引入结构拓扑优化领域。该方法的基本原理是通过建立高一维的水平集函数，以零水平集面隐式表达动态变化的结构边界。Zhu等［12］基于水平集方法提出了一种多点输出柔顺机构的设计方法，该方法无需在输入输出位置施加额外的弹簧装置，优化结果表明该方法可以有效抑制“类铰链”结构的产生。

传统的水平集方法通过求解Hamilton-Jacobi（H-J）偏微分方程实现水平集函数的更新演化，但函数曲面上的点只能通过水平运动来实现拓扑边界的连接与断开，因此传统水平集方法的优化结果依赖于初始设计中孔洞的设置，存在一定的初始设计依赖性。近年来提出的参数化水平集方法［13］在一定程度上改善了传统水平集方法的初始设计依赖性缺陷，但仍存在诸如优化过程不稳定等问题需要进一步解决。

水平集方法在优化过程中的不稳定是由于优化过程中的材料分布不存在中间密度，材料密度的突变易造成不连续的拓扑变化，进而影响优化过程的稳定性。为了克服这一缺陷，Wei等［14］结合变密度法的相关概念提出了水平集带方法，即在零水平集周围引入水平集带，将零水平集面扩大为具有一定宽度的水平集带范围。水平集带区域内的材料密度通过插值可以连续地分布于［0，1］范围内。随着优化过程的推进，水平集带宽度按一定速率逐步减小至0，回归至零水平集面，同时水平集带区域的材料密度也不断向0-1分布靠拢，最终使得优化过程稳定地收敛于最优解。

本文基于引入水平集带的参数化水平集方法，以最大互应变能为目标函数，在材料体积约束下对具有不同初始设计的位移反向器优化问题进行了研究。优化结果表明，水平集带方法可有效地改善柔顺机构优化过程中初始设计依赖性问题，能够得到更加理想的目标函数。此外还研究了具有不规则设计域和考虑非线性效应的柔顺机构拓扑优化问题，证明了该方法在面向实际工程的复杂设计问题中的适用性。

1 引入水平集带的参数化水平集方法

1.1 参数化水平集方法

水平集方法通过高一维度的水平集函数的零等值面隐式表达结构边界，通过更新水平集函数实现结构边界的演化，进而实现结构拓扑形式的改变。水平集函数的定义通常如下：

式中，D为设计域，x∈D表示设计域内任意一点，t为水平集函数演化的伪时间步，Ω为实体材料区域，∂Ω为实体材料区域的边界。水平集函数的形式如图1所示。

图1 水平集函数曲面及其零水平集Fig.1 Level set function and its zero-level set

传统水平集方法通过求解哈密顿-雅可比偏微分方程实现水平集函数的更新，即

式中，Vn为结构边界演化的法向速度场。在参数化水平集方法中，水平集函数通过多个径向基函数插值得到，形式如下：

式中，gk(x)为径向基函数，αk(t)为相应的扩展系数，nk为径向基函数的总数。径向基函数由于其较好拟合性能，近年来被应用在水平集方法中以实现水平集函数的参数化构造［15］。基于径向基函数构造的水平集函数通过扩展系数α(t)的更新实现演化，即

式中，Δt为时间步长，G为与径向基函数分布相关的可逆矩阵，B矩阵的表达式为

式中，δ(φ)为替换|∇φ|的近似函数［13］。

1.2 引入水平集带的参数化水平集方法

参数化水平集方法通过扩展系数的更新实现了水平集函数的演化，但设计域内的材料密度严格遵从0-1分布，使得演化过程中的拓扑变化缺乏连续性，会导致迭代过程不够稳定从而陷入局部最优。鉴于此，Wei等［14］提出了水平集带方法，该方法结合变密度法中材料密度连续变化的优点，在水平集函数的零水平集面周围引入具有一定宽度的水平集带，使得水平集函数的零水平集等值面扩大到相应的带宽范围。水平集带区域内的材料密度可以通过如下的Heaviside函数计算得到：

式中，h为水平集带的宽度，ε为设定的材料密度的最小值，本文算例中同取为0.001。水平集带区域内的材料密度可以通过Heaviside函数插值实现分布于0.001～1之间的连续变化，从而避免优化过程中由于孔洞出现或消失造成的材料密度突变。水平集带宽度的大小对材料密度的影响如图2所示，随着水平集带的宽度的减小，带宽范围内的材料密度逐渐趋近于0-1分布。

图2 水平集带宽度对材料密度的影响Fig.2 Effect of the level set band width on the material density

2 优化模型

柔顺机构的主要设计目的是在输入端施加驱动后，能够在输出端得到目标形式的运动，因此机构必须具有一定的柔性才能保证运动产生。机构的柔性可以通过互应变能（MSE）表示，互应变能越大，表示机构的柔性越大，输出端位移也越大。

式中，J为互应变能，K为结构刚度，U1为在结构的输入端施加实际载荷产生的结构位移矢量，U2为在结构输出端施加单位虚荷载产生的结构位移矢量。以互应变能最大化为目标函数、材料体积为约束的优化模型可以表示为

在上述优化模型中：

式中：J(u，φ)为目标函数，即结构互应变能；u1为输入端施加真实载荷后得到的结构位移；u2为在输出端施加单位载荷后的结构位移；ε为应变张量；C为弹性张量；v为虚位移；U为准许位移场；G(φ)为限制材料用量的体积约束；Vmax为用体积表示的材料最大用量；u0为结构位移边界条件；n为边界法向单位向量；τ1、τ2分别为在输入端和输出端施加的面力荷载；a(u，v，φ)为能量双线性函数；l1(v，φ)、l2(v，φ)分别为上述两种荷载情况下的外力虚功；b为体力，在本文算例中未考虑。H(φ)用于定义水平集函数曲面上某一点的材料密度，通常如下式所示：

引入水平集带后，H(φ)则更新为式（6）的形式，两者最大的区别在于引入水平集带之后，材料允许在迭代过程中存在中间密度。由互应变能密度和控制体积约束的拉格朗日乘子确定如式（14）所示的法向速度Vn后，通过最速下降法对优化问题进行求解。

有关水平集带方法的更多细节可以参考Wei等［14］关于结构柔顺度最小化问题的研究。

3 数值算例

本节通过位移反向器算例以及旋转柔顺机构算例验证水平集带方法在柔顺机构设计中的有效性，并将该方法拓展应用到考虑非线性效应的柔顺机构优化设计问题中。本节的算例都将采用无量纲参数。

3.1 位移反向器

位移反向器的设计域和边界条件如图3所示，设计域被划分为40×40个正四边形单元，左端上、下部固定，输入端和输出端分别施加一根弹性系数为0.1的弹簧。根据对称性，该模型只取上半部分进行计算，设计域下边界施加竖向位移约束，输入端荷载fin大小为1，施加在左端下部，其中实体材料部分的弹性模量E0=1，空材料的弹性模量为Emin=10-3E0，材料的泊松比μ=0.3，最大体积约束为整个设计域体积的30%。

图3 位移反向器设计域及边界条件Fig.3 Design domain and boundary conditions of a compliant inverter

首先采用引入水平集带且基于MultiQuadric样条函数的参数化水平集方法对上述问题进行优化求解，优化过程以及优化结果如表1所示。

表1 位移反向器优化过程及结果Table 1 Optimization process and results of the compliant inverter

优化过程中的中间优化结果始终保持清晰的拓扑边界，最终得到的优化结果也较为合理。此外，从中间优化结果的密度分布中可以观察到明显的灰度区域，反映出该方法与传统参数化水平集方法的区别。为验证水平集带方法的有效性，设定了如表2第1列所示的4种不同初始设计，对比了未使用和使用水平集带的优化结果。表2中的第1列为4种不同的初始设计，第2列对应各初始设计下未引入水平集带的优化结果，第3列对应引入水平集带的优化结果。水平集带初始宽度设置为5，每一个迭代步减小0.1。表2也给出了各初始设计对应的优化结果目标值。从优化结果的拓扑形式来看，引入水平集带方法和未引入水平集带方法的优化结果拓扑形式相似，在不同的初始设计下均能得到相似的结果。但引入水平集带的优化结果拓扑形式更为相近，且受初始设计的影响更小；从目标函数值来看，各初始设计下在引入水平集带后优化结果的输出端位移更大。从优化结果的差异性来看，未引入水平集带方法的4种初始设计得到的目标函数值标准差为9.96×10-3，而引入水平集带的目标函数值标准差减小为1.76×10-3，较为明显地缓解了参数化水平集方法对初始设计的依赖性。此外，对比引入和未引入水平集带方法优化结果的几何特征可以发现，引入水平集带后输出端的横向杆件长度均小于未引入水平集带时的长度。在该杆件长度较小的情况下，位移反向器获得了更大的位移。图4展示了表2第1行优化结果的应变能分布，可以观察到引入水平集带后的优化结果（图4右）中，类铰链处应变能相对较小。

表2 不同初始设计的位移反向器的优化结果Table 2 Optimal results of the compliant inverter with different initial designs

图4 参数化水平集方法优化结果的应变能分布Fig.4 Strain energy distribution of the optimal results using parameterized level set method

3.2 旋转柔顺机构

随着微型机电系统的发展，具有特定力学性能的柔顺机构也逐渐成为研究的热点。旋转柔顺机构要求在输入端施加荷载后，能够在输出端形成旋转力矩。例如图5所示的由6个三角形组成设计域的旋转机构设计问题，当特定位置同时施加荷载作用时，机构中心处会形成力矩拉动中部杆件旋转运动［16］。考虑对称性时，该优化问题的设计域及边界条件如图6所示。

图5 旋转柔顺机构设计问题Fig.5 Design problem of a rotational compliant mechanism

图6 旋转柔顺机构设计域及边界条件Fig.6 Design domain and boundary conditions of a rotational compliant mechanism

由于该优化问题的设计域为三角形，不宜采用正四边形网格进行离散化。得益于参数化水平集方法在处理具有非结构化网格的优化问题上的优势，本算例将该模型划分为12 532个三角形单元，共有6 444个节点，最大体积约束为设计域体积的30%，水平集带初始宽度设置为5，每个优化迭代步减小0.1。该优化问题采用SIMP方法和未引入水平集带的参数化水平集方法以及引入水平集带的参数化水平集方法的优化结果分别如图7（a）、7（b）、7（c）所示，采用水平集带方法的优化结果拼装为整体后的效果如图8所示。该算例中引入了水平集带的参数化水平集方法的优化结果与基于SIMP方法的优化结果有一定的相似性，优化结果的目标函数值为1.244 2，而未引入水平集带的优化结果目标函数值为1.130 7。可见引入水平集带使得材料密度可以连续变化，从而更有利于寻找优化问题的全局最优解。同时对具有非结构化网格柔顺机构优化问题的成功求解也证明了该方法在面向工程的复杂设计问题上的有效性。

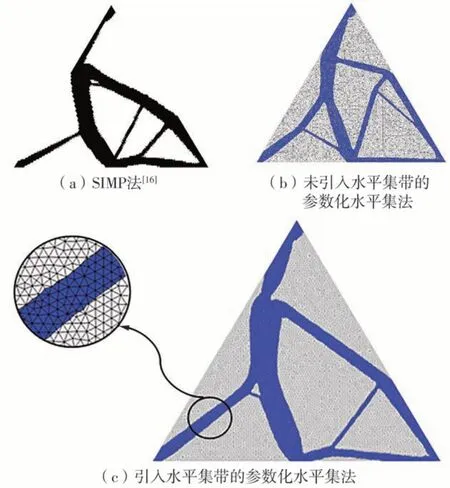
图7 SIMP法和参数化水平集方法的优化结果对比Fig.7 Comparison of optimal results using SIMP method and parameterized level set method

图8 旋转柔顺机构优化结果Fig.8 Optimal result of the rotational compliant mechanism

3.3 大变形位移反向器

柔顺机构通过自身的变形来实现力、能量或位移的传递。仅在小变形范围内工作的柔顺机构功能受到严重限制，因此实际工程中往往需要能够产生大变形的柔顺机构，其输出力与位移之间的关系呈非线性。以考虑大变形效应的位移反向器优化设计为例，根据对称性取上半部分模型进行计算，图9为位移反向器的设计域和边界条件。

图9 考虑大变形效应的位移反向器设计域及边界条件Fig.9 Design domain and boundary conditions of a compliant inverter with large deformation

该设计域划分为100×50个正四边形单元，共5 151个节点，两侧添加的弹簧以及其他边界条件与3.1中算例相同。为了克服求解过程中单元严重畸变造成的数值求解困难，本文采用Luo等［17］提出的附加超弹性单元方法改善数值不稳定现象。本算例的原始单元材料采用Neo-Hookean模型，附加超弹性单元材料采用Yeoh模型［18-19］。

考虑大变形效应后，未引入水平集带和引入水平集带的参数化水平集方法的目标函数和优化结果分别如表3和表4所示。此算例中目标函数值同时也为输出端位移值的负值。在不同初始设计条件下，算例中未引入水平集带方法的优化过程基本不够稳定，迭代曲线有比较明显的震荡现象；而引入水平集带后优化过程的稳定性明显改善，其中初始设计为全实体材料的算例1的优化过程如图10所示。引入水平集带方法后，优化结果的目标函数值比未引入水平集带时平均提高了6.37%。水平集带同样能改善考虑几何非线性效应柔顺机构优化问题的初始设计依赖性，表4中不同初始设计算例在未引入水平集带时其优化结果结构形式相差较大，目标函数值的标准差为2.86×10-4，而引入水平集带后，其优化结果在结构形式上更为相似且材料分布更为合理，目标函数值的标准差减小为4.33×10-5。本节算例的优化过程和优化结果表明引入水平集带的参数化水平集方法在求解考虑大变形效应的柔顺机构拓扑优化问题时能够得到合理的优化结果和理想的目标函数，更好地改善初始设计依赖性问题；且相对于未引入水平集带的参数化水平集方法，优化过程更加稳定，迭代曲线更加光滑，最终可以得到相对更加合理的拓扑形式。

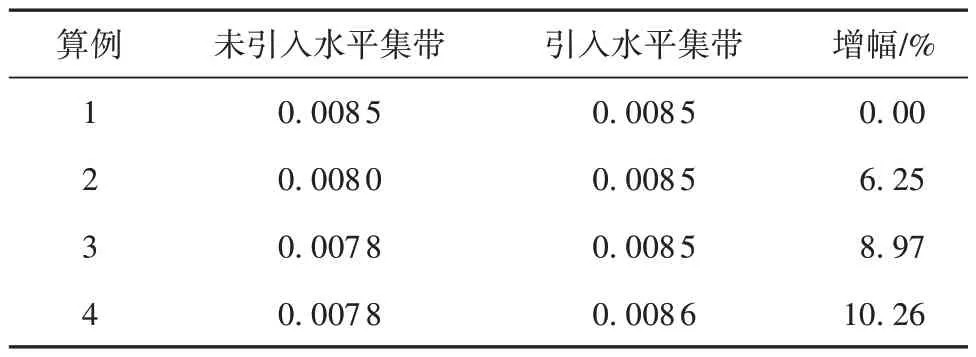
表3 大变形位移反向器的优化目标函数值Table 3 Objective function values of the compliant inverter with large deformation

表4 大变形位移反向器的优化结果及输出端位移收敛曲线Table 4 Optimal results and convergence curves of the output displacement of the compliant inverter with large deformations

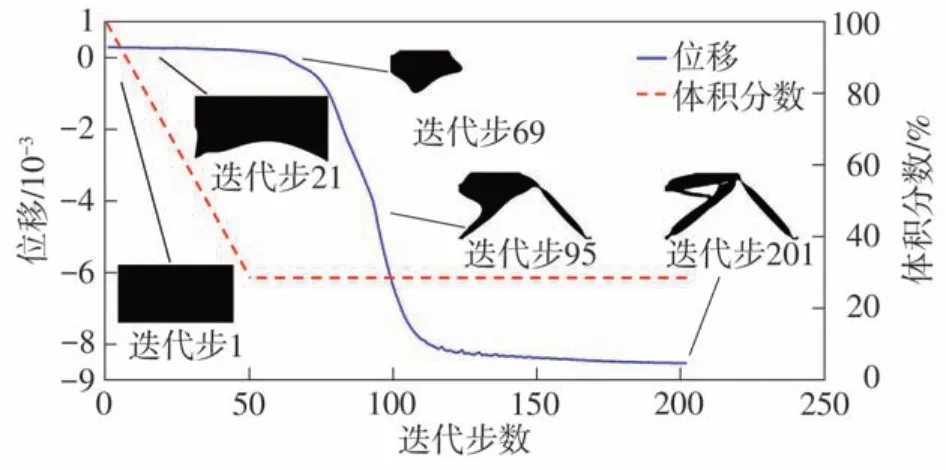
图10 考虑大变形效应的位移反向器问题的输出端位移和体积分数收敛曲线（算例1）Fig.10 Convergence curve of the output displacement and material volume fraction of the compliant inverter with large deformations （Example 1）

4 结语

本文基于引入水平集带的参数化水平集方法，对柔顺机构拓扑优化问题进行了研究。通过位移反向器、具有不规则设计域的旋转柔顺机构及考虑大变形效应的位移反向器优化算例，显示出引入水平集带的参数化水平集方法在柔顺机构优化设计问题中的有效作用。在参数化水平集方法中引入水平集带使得带宽范围内的材料密度连续变化，增强了优化过程的稳定性；同时有效地缓解了优化结果对初始设计的依赖性，得到了更优的目标函数值。

本文的柔顺机构优化模型以最大互应变能作为单一目标函数来衡量机构的柔性，但实际工程应用中的柔顺机构还需要一定的刚度来承受荷载以保证正常工作。此外，根据目标需求的不同，柔顺机构还需要具有多点输出、恒定输出力等多种性能指标。因此多功能柔顺机构优化设计是当前重要的研究方向，也是未来的研究工作。