基于残差密集网络的智能超表面信道估计算法

郑娟毅 董嘉豪 张庆珏 杨溥江 郭梦月 杨朴真

（西安邮电大学 通信与信息工程学院，陕西 西安 710121）

智能反射面［1］（RIS）是未来无线通信一项有前途的技术，可在非视距通信的环境下提供一条全新链路来保障无线通信。RIS也可辅助现有MIMO［2］通信，通过提供基站（BS）-RIS-用户（USER）的级联链路来提高传输效率。RIS由大量无源的可配置反射元件组成以适应实际环境，从而在低功耗的情况下提高传输质量。与传统无线中继［3］相比，RIS技术填补中继法中的空白：RIS是一个具有全双工协议的透明中继，可实时控制传播。使用RIS不需要信号放大器，只需要控制可重构硬件中的功耗。因此以更低的能耗和成本实现大规模RIS。基于以上优点，RIS辅助MIMO通信系统和相关研究已经引起学术界和业界广泛关注。

信道估计需要从接收数据中估计出假定的信道模型的参数。RIS辅助MIMO通信中RIS是被动的，需要对RIS到用户和RIS到基站的信道进行联合估计。联合估计过程存在两个困难：①级联信道不满足传统的瑞利衰落，最优最小均方误差（MMSE）涉及多维积分，实现困难。此外使用传统的LMMSE和LS估计与MMSE估计存在差距。②大量RIS元素导致级联信道是高维度的，由传统方法进行信道估计的硬件成本是高昂的。为了克服困难①，文献［4］中，通过每个时隙仅打开一个RIS发射元件，为单用户系统开发了二进制发射控制的LS信道估计方案。BS处仅接收来自直接链路的干扰，而不接收来自其他发射元件的干扰［5］。这种情况下基站可以连续估计级联信道，然而二进制反射每次只能激活一个元件，因此在BS处只能获得小的信噪比（SNR）用于估计。此外存在大量RIS元素给系统带来长延迟。为了进一步提升接收SNR和缩短信道估计的时间，文献［6］中提出在每个时隙打开RIS的所有反射元件，作者提出了一种基于离散傅里叶变化训练的最小方差无偏估计器，可以达到较高估计精度。文献［7］中开发了两种基于并行因子（PARAFAC）的方法，首先使用LS估计器获得粗略的信道系数，其次利用最小平方Khatri-Rao因子分解和双线性估计技术获得更精确的估计结果。为了克服困难②，文献［8］和［9］中开发了基于子信道估计方案，其中RIS被分为几个独立的子表面，每个子表面由一个公共相移的多个相邻反射元件组成。采用共享策略，训练开销显著降低。文献［10］中引入了级联信道估计框架，并提出了基于系数矩阵分解和矩阵补全的相关算法。文献［11］中研究了RIS辅助MIMO通信系统中的信道估计。首先将信道估计问题转化为恢复稀疏信道矩阵的问题，再提出一种基于压缩感知方案来研究级联信道的稀疏性问题。文献［12］和文献［13］中，研究RIS在多用户系统中的应用，此外开发了三阶段信道估计框架，通过利用不同用户反射信道中的冗余来缩短信道估计框架。文献［14］开发了一种新的RIS架构，配备了单个有源射频（RF）链，用于RIS侧的信道估计，进一步降低训练开销。然而问题1中有限的信道估计性能并未得到很好的提升。

与传统的模型驱动方法相比，数据驱动深度学习（DL）技术［15-17］已经证明了其在RIS辅助通信系统中的有效性，例如基于DL的无源波束形成设计［18-21］，基于深度强化学习（DRL）的相移优化［22］，以及基于DRL的RIS辅助多用户通信（RIS-MUC）系统安全无线通信［23］。基于DL的方法是可行的，然而仍需在RIS辅助通信系统中首先进行信道估计。文献［23］中提出使用DnCNN结合残差网络来建立模型。综上所述，为进一步提高RIS信道估计的精度，将RIS-MUC系统中的信道估计问题建模为去噪问题，开发基于深度残差（DReL）的信道估计框架。将LS估计值作为粗估略值，其次使用RDN网络对粗估略值进行进一步优化。RDN网络具有深度网络的高速度优点，不需要任何先验统计信息，仿真结果表明该算法进行RIS辅助MIMO通信的信道估计具有良好的性能。

1 系统模型

本文设计了一种时分双工（TDD）的系统模型。由单基站、单RIS和K个用户组成。基站处配置M单元天线阵列，RIS处配置N个无源发射元件。由于TDD模型的互易性，设计考虑上行链路。

如图1所示为TDD上行链路模型。

图1 RIS辅助MIMO通信系统模型Fig.1 Model of RIS-assisted MIMO communication system

Uk，k∈(1，2，…，K)为第K个用户。BS-RIS、RIS-USER和BS-USER的信道链路为G∈LM×N，fk∈LN×1和dk∈LM×1。Uk-RIS-BS的信道可以表示为Bk=GRfk∈LM×1，其中R=diag(r)∈LN×N；r=[βejφ1，βejφ2，…，βejφN]T为相移矩阵；0≤β≤1、0≤φn≤2π分别表示第n个点的振幅和相移，n∈{1，2，…，N}；L表示复数矩阵。Uk-RIS-BS的信道可以通过相移矩阵R来改变。diag(r)fk=diag(fk)r，Uk-RIS-BS的信道可以重写为Gdiag(r)fk=Gdiag(fk)r。

因此，上行链路信道为

式中，

式中，dk为直接信道，Bk为级联信道。

在此基础上，根据RIS辅助通信系统设计信道估计协议，如图2所示。

图2 导频子帧结构Fig.2 Pilot subframe structure

采用K个正交导频来区分不同用户Uk，k∈{1，2，…，K}，导频子帧长度为L，L≥K，每个用户的导频表示为uk=[uk，1，uk，2，…，uk，L]T，每个用户的功率为ω。其中uHkuk=ωL并且uHaub=0，a，b∈{1，2，…，K}，a≠b。

信道估计阶段由C个子帧组成，每个子帧由L个导频符号组成。对于系统而言，相移矩阵在一个子帧内保持不变，并且能针对不同的子帧切换到不同的相移矩阵。对于第k个用户Uk，在每个子帧中发送标识导频序列Uk，因此第c个子帧中基站处接收导频信号向量为

式中：HK为需要估计的信道矩阵；pc=[1，rc]T∈L(N+1)×1；vc，l∈LM×1表示基站处第c个子帧中第l个采样噪声向量。噪声矢量用服从高斯分布的噪声vc，l～(0，σ2vIM)来描述，σ2v为每个天线的噪声方差，I为单位矩阵。在基站处第c个子帧期间将L个接收信号向量堆叠成矩阵形式：

式中，Sc=[sc，1，sc，2，…，sc，l]表示接收信号矩阵，Vc=[vc，1，vc，2，…，vc，l]表示噪声矩阵。两个用户间导频序列是正交的，通过将不同序列导频相乘来分离来自Uk的接收信号，即

式中，P=[p1，p2，…，pc]，pc=[1，rc]T，Z=[z1，k，z2，k，…，zc，k]，P∈L(N+1)×C，pc∈L(N+1)×1，Z∈LM×C。因此信道估计就是利用XK和P恢复出真实矩阵HK。

2 基于RIS辅助通信系统信道估计

信号通过信道传输时会出现衰减，此外信道干扰和噪声也会对信号产生影响，导致信号失真。为了正确译码，需要从接收到的信号中去除信道造成的噪声和干扰。为了实现这一目的，需要了解信道的特性，这个过程称为信道估计。本节首先介绍DnCNN算法和RDN算法，其次提出结合RIS辅助MIMO信道估计的DReL框架，最后利用不同算法进行信道估计。

2.1 用于信道估计的DnCNN算法

DnCNN是一种经典去噪算法，结合CNN和ResNet的残差学习。将网络学习过程中的噪声输出改为残差，直接得到预测的信道。

如图3所示为一个去噪块，整个模型包括3个去噪块。其中每个去噪块包括15层，其中1-14层由Conv+BN+ReLU层组成，第15层由Conv层组成，Conv表示卷积，BN表示批量归一化，ReLU表示激活函数，每个去噪块的原始输出为噪声，经过残差减可以得到不含噪声的输出。卷积核大小为3×3，卷积神经网络的输入通道数为2，内部每层输出通道为64，最后一层输出通道数为2。

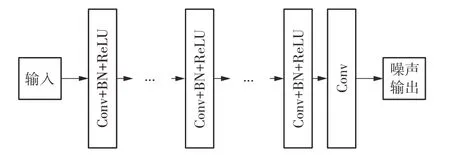
图3 DnCNN算法Fig.3 DnCNN algorithm

DnCNN算法以较高准确率来进行信道估计，然而在实际的训练中，大数量RIS会导致参数量过多和训练时间长。实际中RIS信道估计需要更快的训练速度和更高的训练精度。综上所述提出基于RDN网络的学习框架。

2.2 用于信道估计的残差密集算法

本节中提出一种基于深度学习的残差密集网络（RDN）算法。RDN网络结构如图4、图5所示。

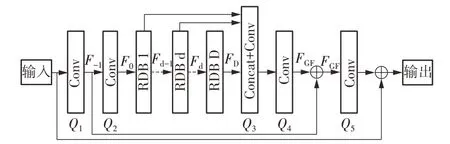
图4 RDN网络Fig.4 RDN network

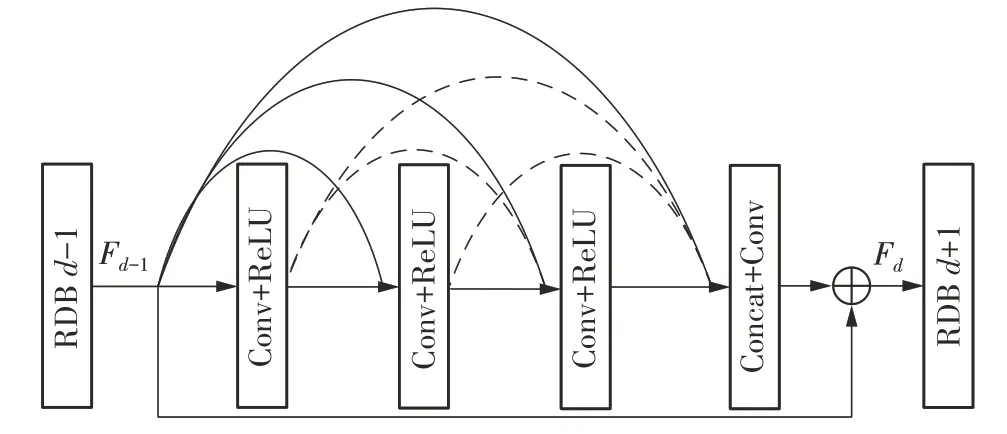
图5 RDB网络结构Fig.5 RDB network structure

RDN由多层卷积层构成，其中Concat表示叠加融合。卷积神经网络的输入通道数为2，内部每层的输入和输出通道数为16，第7层的输出通道数为16。RDB表示RDB块，RDB可以融合所有卷积层的信息，来稳定训练并结合深层和浅层特征，从含噪信道中更快收敛并达到更好的估计性能。

RDB由多个卷积层组成，每个RDB的输入和输出通道数为16。RDB由4个卷积层组成，使用跳跃连接，第1、2、3个卷积层的卷积通道分别为24、32和40。最后使用Concat+Conv控制输出通道数为16，来保证可以进入下一个RDB块。以用来融合来自所有卷积层的信息。其中Fd-1和Fd分别是第d个RDB的输入和输出。

式中，HRDB，d为第d个RDB的运算，HRDB，d为一个包括多层卷积和ReLU的运算复合函数。

RDN算法在图像超分辨率重建领域得到广泛应用，其非线性建模能力可以更好的适应RIS辅助通信系统中的非线性信道估计问题。例如RIS的发射系数的非线性优化和RIS引入的非线性传输特性，因此RDN算法的非线性建模问题可以应对这些问题。此外RDN算法利用深度神经网络的特征学习能力，可以从大量数据集中学习有用的特征表示，从而提高信道估计的准确性和鲁棒性。经过深度学习网络的优化和设计，可以在计算效率和准确性之间取得平衡。对于RIS辅助通信系统，信道估计是一个计算密集的任务，尤其是在大规模MIMO和高数据速率的场景下。RDN算法可以通过参数共享和网络优化等技术，提高计算效率，适应实际的通信系统需求。

2.3 基于RIS辅助MIMO信道估计框架

首先介绍LS估计器，根据文献［24］使用LS估计：

式中，P†=PH(PPH)-1表示P的伪逆［24］。

数据流中的每个帧具有相同的帧结构，分为信道估计阶段和数据传输阶段。在信道估计阶段，RIS总共生成C个相移矩阵，C≥N+1。通过C个不同相移矩阵的不同传输模式完成通信。

式中，RC=diag(rC)是第C个相移矩阵，rC=[βejφC，1，βejφC，2，…，βejφC，N]T，0≤β≤1，0≤φn≤2π分别表示第C个相移矩阵下RIS的第N个元素的幅度和相移。

根据文献［6］，在提高基站接收信号功率方面，P的最佳方案是将P设计成离散傅里叶变化（DFT）

式中，WC=ej2π/C，PPH=CIN+1，其中IN+1为单位矩阵。不同的C由式（9）中的RIS相移矩阵Λ=[R1，R2，…，RC]T产生。由于LS估计量一个显著特征是不需要统计特性而被广泛使用。LS估计误差为

由式（5）和（6）可得：

式中，=XkP†∈LM×(N+1)表示基于LS估计器的噪声观测，而=ZKP†∈LM×(N+1)。

基于去噪模型，开发基于DReL的信道估计框架，分为离线训练阶段和在线评估阶段。离线阶段使用大量的训练数据对RDN网络进行训练；在线评估阶段，将测试集信号输入完成训练的RDN网络模型，即可以得到估计信道具体步骤如图6所示。

图6 基于RDN模型的离线训练和在线估计阶段Fig.6 Offline training and online estimation stage based on RDN model

离线训练阶段，由式（6）可知原始训练集为

式中，X(i)k、H(i)k为第i个i∈{1，2，…，Nt}训练实例的输入。将(X，H)输入到LS估计器，获得基于LS的训练集

式中，中的θ表示RDN的总参数。根据MMSE准则可以通过最小化贝叶斯均方误差得到最优MMSE估计量但在实际中训练样本是有限的，因此统计贝叶斯MSE（均方误差）不可用，采用经验MSE，可定义为

显而易见，当Nt趋于无穷时，RDN估计器收敛于MMSE估计量，可使用数据驱动方法通过最小化经验MSE来训练模型，而MMSE通过最小化基于先验概率分布函数的贝叶斯MSE，属于一种模型驱动方法。此时用经验MSE作为成本函数，损失函数可表示为

基于此，采用反向传播逐步更新网络中每一层的参数来获得训练良好的RDN即

式中，θt、θt+1分别为第t次和t+1次迭代的权重，g(θt)为θt的梯度变量，ηt为学习率。即基于RDN的估计器可以表示为

式中，͂为基于LS的输入，θ*为通过最小化JMSE(θ)训练良好的网络参数。

在线评估阶段，给定测试数据采用LS估计器获得其粗略估计值，送入训练好的模型中，得出信道系数矩阵：

最后将实部和虚部进行组合即为最终估计信道。

为了更深入了解所提出的估计算法，从理论分析其特性，将所提出的RDN算法显式表示为数学函数，并从理论上分析RDN的输出。为了方便分析，将信道矩阵视为网络输入，这种情况下输入矩阵变成二维矩阵：

式中，Ql为不同卷积层权重系数。由式（7）可得F1，…，FD，其中[F1，F2，…，FD]表示矩阵融合矩阵。根据式（8）和式（21）可得：

式中，T为已训练完成的矩阵，因此提出的RDN是一个数据驱动的非线性估计器，采用大量样本的训练特征可以提高其估计精度。此外根据文献［23］和［24］可得：

式中，RHk=E(HHKHK)表示统计信道相关矩阵［24］。RDN估计器可作为一般化的模型，根据式（23）和（24）可得：当时，RDN估计器等价于LMMSE估计器，即所提出的RDN估计器能够实现和LMMSE估计器相同的性能。当Hk的先验概率密度是高斯概率密度时，LMMSE估计器和MMSE估计器相同，所提出的RDN估计器可以实现最优MMSE性能。当Hk的先验概率不满足高斯概率密度函数时，最优MMSE不具有闭合形式，且LMMSE估计只能从基于二阶信道相关矩阵获得有限估计性能。

3 仿真结果

本节中验证提出的RDN算法用于信道估计，在Rician路径损耗模型上进行实验。首先对实验参数和实验背景进行描述，其次从估计精度和算法参数量来验证RDN算法的性能，最后与DnCNN、LS［24］、B-LMMSE［4］和E-LMMSE算法进行对比。

3.1 实验参数设置

RIS-MUC系统配备M个天线的基站、N个RIS反射元件和K个单天线用户。RIS以连续相移运行，系统的默认设置为M=8、N=32、K=6、C=N+1=33。模拟中采用了路径损耗模型，信道路径损耗建模为αUBk=α0(λUBkλ0)-Υ1，αURk=α0(λURkλ0)-Υ2，αRBk=α0(λRBkλ0)-Υ3。式中：αUBk、αURk和αRBk分别表示Uk-BS、Uk-RIS和RIS-BS的路径损耗；γi，i∈{1，2，3}表示路径损耗指数，γ1=3.6，γ2=2.3和γ3=2；λ0=10 m表示参考距离；α0=-15 dB表示参考距离处的路径损耗；λUBk、λURk、λRBk分别表示Uk-BS、Uk-RIS和RIS-BS的距离；λUBk=100 m，λURk=16 m，λRBk=90 m。所有信道设定为Rician衰落模型，表征小尺度衰落。在这种情况下，RIS-BS链路信道表示为

式中：βRB为RIS-BS信道的Rician因子：GLOS、GNLOS分别为直射分量和瑞利分量。当βRB→∞时，G等价于莱斯信道，当βRB→0时，G等价于瑞利信道。将Uk-BS和Uk-RIS通道的Rician因子分别定义为βUB和βUI。为了考虑路径损耗因子的影响，G中的元素应乘以。设置βUB=0、βUR=0和βRB=10。在Matlab中进行数据集的生成，其中训练集、验证集和测试集的大小为80 000、20 000和20 000。训练的Batchsize设为32，使用Adam优化器对RDN网络参数进行优化，初始学习率设置为0.001，其他采用默认参数。本文在Windows系统下对Pytorch框架进行仿真，在硬件为I5-8300H和RTX1050Ti的支持下完成训练和测试。

3.2 实验结果和分析

采用归一化均方误差（NMSE）rNMSE作为估计性能度量：

式中，͂、H分别为信道估计值和信道真实值。此外仿真结果中使用的信噪比（SNR）指的是发射SNR，即SNR=ω/σ2z。同时提供了以下算法仿真进行比较：LMMSE方法、LS方法、二元反射控制LMMSE（B-LMMSE）方法和残差网络（ResNet）方法。对于B-LMMSE方法，利用文献［4］中提出的二进制反射控制策略，与此同时采用LMMSE估计器进行信道估计。通过对105个蒙特卡罗实现的性能进行平均，获得了所示结果的每个仿真点；其次在NMSE方面验证所提出的RDN算法的信道估计性能，并分别揭示NMSE与SNR和信道维数的关系；最后研究复杂度分析。

3.2.1 NMSE和SNR的关系

为了验证RDN算法的有效性，如图7所示对比了信噪比在0、5、10、15、20和25 dB下5种算法的NMSE性能。

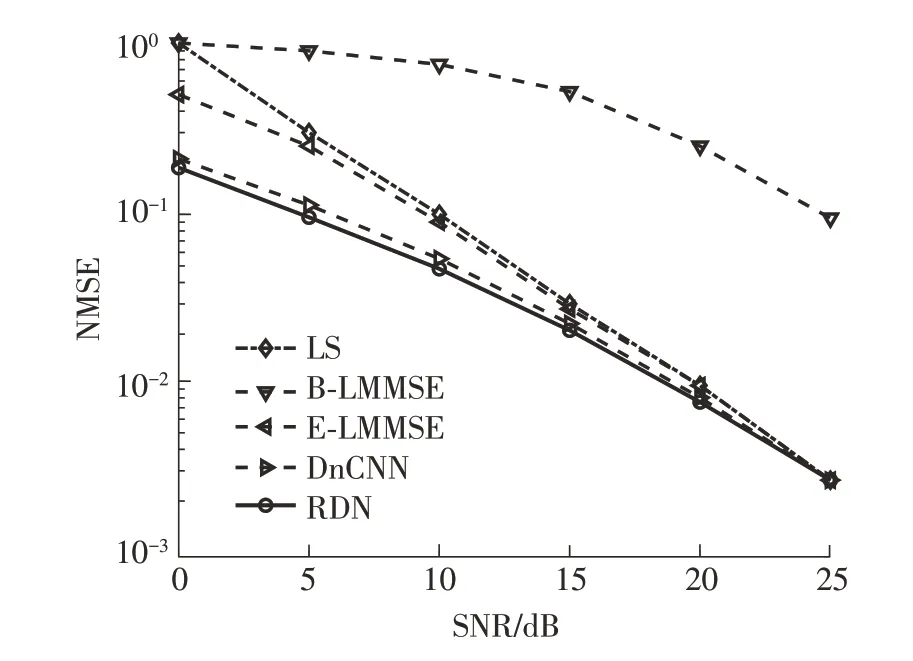
图7 不同信噪比下各个网络模型的NMSE性能比较Fig.7 NMSE performance comparison of various network models under different signal-to-noise ratios

由图7结果可知，5种算法的NMSE指标都随着SNR的增大而减小，其中DnCNN算法和RDN算法性能显著优于其他3种算法；LS、E-LMMSE算法显著优于B-LMMSE算法，特别是在高SNR区域。因为对于每个时隙，当采用DFT控制策略时，所有N个元件都被接通以反射入射信号，而在二进制控制策略下仅一个RIS元件被接通，导致用于B-LMMSE信道估计的接收信号功率不足。在信噪比SNR=5 dB时，所提出的RDN较对比算法中最优的DnCNN算法的lgrNMSE降低约0.70 dB，较次优的LS和E-LMMSE算法的lgrNMSE分别降低约6.02和4.95 dB，较B-LMMSE算法的lgrNMSE降低约9.72 dB。该结果验证了所提算法在信道估计中的优势。

3.2.2 NMSE和RIS数量N的关系

信道维数也是影响估计性能的重要参数。为了验证所提出的RDN的可扩展性，进行了仿真以评估不同信道维度下的NMSE。由N表示的RIS元素的数量直接影响信道矩阵Hk的列数，如图8所示绘制了不同算法的NMSE与N的变化关系。其中M=8，C=N+1，信噪比为5 dB。

图8 不同RIS数量下各个网络模型的NMSE性能比较Fig.8 NMSE performance comparison of various network models with different RIS numbers

由图8结果可知，LS、E-LMMSE、DnCNN和RDN算法的NMSE随着N的增加而减少，而基于NMSE二进制控制策略的方法，即B-LMMSE算法，对于不同的N几乎保持恒定值。这是因为尽管RIS处的反射元件总数不同，B-LMMSE算法在每个时隙仅打开一个元件。此外，所提出的RDN算法在所有考虑的算法中仍然实现了最佳性能，在RIS数量为32时，所提出的RDN较对比算法中最优的DnCNN算法的lgrNMSE降低约0.71 dB，较次优的LS和E-LMMSE算法的lgrNMSE分别降低约5.28和4.08 dB，较B-LMMSE算法的lgrNMSE降低约9.78 dB。

3.2.3 NMSE和基站天线数量M的关系

为了验证所提出的RDN的可扩展性，进行了仿真以评估不同信道维度下的估计性能。如图9所示绘制了不同算法的NMSE与M的变化关系。其中N=16，C=17，信噪比为10 dB。

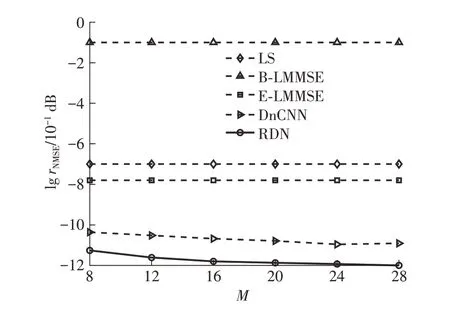
图9 不同基站天线个数下各个网络模型的NMSE性能比较Fig.9 NMSE performance comparison of various network models with different base station antennas

BS处的天线数量（表示为M）决定了信道矩阵Hk的行数，这在估计性能中也起着重要作用。因此，图9研究了M对NMSE性能的影响。很明显，NMSE对M的变化不敏感。这是因为在NMSE的计算中，由于分子中实现的M增加而产生的阵列增益被分母中的M抵消。在基站数量为16时，所提出的RDN较对比算法中最优的DnCNN算法的lgrNMSE降低约1.12 dB，较次优的LS和E-LMMSE算法的lgrNMSE分别降低约4.02和4.78 dB，较B-LMMSE算法的lgrNMSE降低约10.79 dB。

3.2.4 NMSE和导频长度C的影响

为了验证所提出的RDN算法在不同导频长度下的性能，进行仿真以评估不同信道维度下的估计性能。如图10所示绘制了不同算法的NMSE与C的变化关系。其中M=8，N=16，信噪比为5 dB。

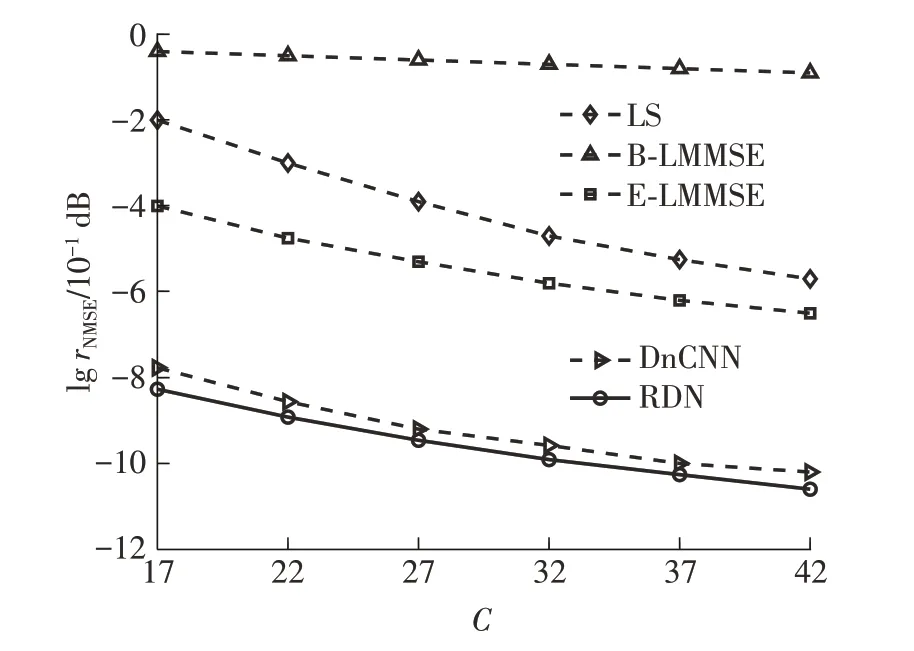
图10 不同导频长度下各个网络模型的NMSE性能比较Fig.10 NMSE performance comparison of various network models with different pilot lengths

如图10所示，所有算法的NMSE随着导频数量的增加而减少，并且不同方法相对于C具有不同的斜率。特别是，B-LMMSE算法的NMSE随C的增加而缓慢下降，而LS、E-LMMSE、DnCNN和RDN算法的NMSE急剧下降。原因在于，对于B-LMMSE算法，基站接收信号的功率非常有限，仅为其他方法的1/N倍。在导频长度为27时，所提出的RDN较对比算法中最优的DnCNN算法的lgrNMSE降低约0.26 dB，较次优的LS和E-LMMSE算法的lgrNMSE分别降低约5.56和4.16 dB，较B-LMMSE算法的lgrNMSE降低约8.86 dB。此外，所提出的RDN可以利用来自更大尺度输入矩阵的更可区分的空间特征来提高估计精度，从而在所有考虑的算法中实现最佳性能。

最后从参数对DnCNN算法和RDN算法进行评估。DnCNN算法和RDN算法比较，RDN算法减少了参数量。且在实际训练中，RDN由于更好的利用了数据特征，实际部署时间也小于DnCNN算法。

算法参数量对比见表1。

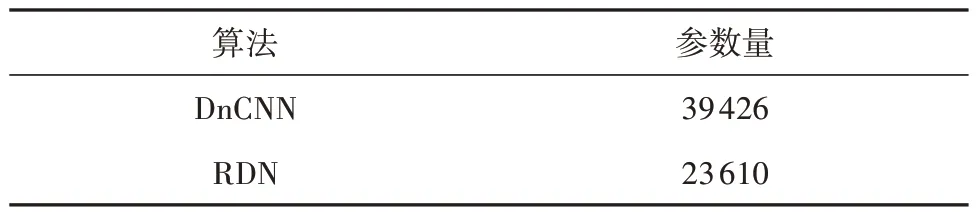
表1 算法参数量对比Table 1 Comparison of algorithm parameters

参数量衡量了离线训练阶段需要部署的时间长短、需要的设备硬件性能。RDN比DnCNN算法减少约40%的参数量，且显著降低了NMSE。

接下来从计算复杂度对比RDN算法和传统算法，传统算法中B-LMMSE和E-LMMSE有相同的计算复杂度，统一用LMMSE代替。LS和LMMSE算法不需要离线训练，可直接进行在线估计；LS在线估计复杂度为O(MClog2(MC))，LMMSE在线估计复杂度为O(C3+MC2)，RDN在线估计复杂度为离线训练复杂度为其中n0为输入维度，nl、kl为第l层神经网络通道数和卷积核尺寸，l∈{1，2，…，Nl}，Nt为训练集数量，It为最大迭代次数，M为星站天线数。LS可以通过快速傅里叶逆变换来实现，LMMSE计算复杂度主要来自矩阵求逆，与LS和LMMSE相比RDN算法的计算复杂度较高，但获得了性能上的大幅提升。在实际应用中利用GPU加速和神经网络的并行计算能力可以减少离线训练和在线估计时间。因此本文提出的算法是具有实际可行性的，表现出了显著优势。

4 结论

在8个天线基站、32个RIS反射元件和6个单天线用户的系统参数设置下。RIS以连续相移运行。在相同条件下，使用NMSE作为性能度量标准。所提出的RDN算法较对比算法中最优的DnCNN算法的lgrNMSE降低约0.70 dB，较次优的LS、E-LMMSE算法的lgrNMSE分别降低约6.02和4.95 dB，较B-LMMSE算法的lgrNMSE降低约9.72 dB。