特征域近端高维梯度下降图像压缩感知重构网络

杨春玲 梁梓文

（华南理工大学 电子与信息学院，广东 广州 510640）

压缩感知理论［1］表明，对于具有稀疏性质或可以被稀疏表示的信号，能够通过欠采样（远低于奈奎斯特采样频率）方式完成对该信号的采样，同时实现该信号的压缩。对于信号编码端计算资源受限的场景，应用该理论能够极大缓解编码端的计算压力。在该理论中，给定观测矩阵Φ∈RM×N(M≪N)，原始信号x∈RN×1能够被Φ测量，实现高维到低维的线性映射，进而获得低维的测量值y∈RM×1，数学过程可表示为：

然而，利用测量值y重构原始图像信号x是一个病态的逆问题，如何高精度重构原始图像信号是图像压缩感知重构算法研究的重点，也是难点。过去的传统算法通过人工设计图像信号的特征表示，构造信号的多假设集合［2］或信号的组稀疏表示［3］，利用迭代优化算法完成优化问题的求解。然而粗糙的参数设计以及高计算复杂度等问题，造成此类方法的泛化性能不佳，重构速度慢等不足，限制了实际的应用。近年来，深度学习的引入打破了传统算法的限制，此类算法以数据驱动的方式学习信号的特征表示，具有更强的泛化性能和更快的推理速度。根据是否受传统优化理论指导，基于深度学习的图像压缩感知重构方法可以被划分为两大类：基于“黑盒”的网络设计和基于优化启发的网络设计。

“黑盒”设计方法［4-8］利用深度神经网络将测量值直接映射为输出图像。早期，级联的卷积神经网络［4］或残差结构［5］被用于设计重构网络，以简单的网络架构取得卓越的重构性能和极快的推理速度吸引了大量研究人员关注。后来，一些更复杂的网络架构被提出以取得更高精度的图像重构性能，文献［6］中提出采样和重构网络的联合优化，使用可学习的采样矩阵代替固定的随机高斯矩阵，更充分地完成信号的采样。文献［7］中引入非局部注意力机制建模图像的非局部相关性，实现更好的图像纹理细节恢复。文献［8］中提出多尺度残差对抗生成网络，并引入感知损失函数以恢复更准确的图像结构信息。

与上述方法不同，基于优化启发的图像压缩感知重构网络设计［9-23］受传统优化理论指导，在每个优化阶段利用测量值补充缺失信息。其中，最具代表性的是近端梯度下降算法［24］指导的网络设计，Zhang等［10］利用迭代收缩阈值算法（ISTA）完成网络的设计，提出了ISTA-Net，并依据这套理论先后提出了OPINE-Net［11］、ISTA-Net++［12］、Coast［13］，展现了基于优化启发的深度展开网络卓越的重构性能；与ISTA此类近端梯度下降算法指导不同，文献［14］中引入交替方向乘子法（ADMM），将网络的每一个优化阶段展开为对多个子问题的优化；文献［15］中引入近似消息传递（AMP）算法，将图像的重构问题看作信号的去噪问题。近期，大量工作从网络架构或从信息优化的角度上完成重构网络的设计。文献［16］中引入长短时记忆网络以增强网络在前馈时信息的联系；文献［20］中引入Fast-ISTA算法，并构造多尺度的网络学习分支从不同尺度上完成图像信号的恢复；文献［21］中将卷积网络替换为具有全局建模能力的Transformer架构，实现更好的图像恢复效果；文献［25］中提出基于ISTA算法设计的Transformer与卷积网络的混合架构，通过充分结合两种架构的优点实现高质量图像恢复；文献［26］中提出动态路径选择思想，通过控制单元决定优化阶段的执行，实现性能与复杂度的权衡。上述优化启发工作均在单一图像域执行梯度下降，随后将梯度下降结果映射至高维特征域作进一步的去噪处理，这些方法符合理论设计，然而从特征利用的角度来看，前一阶段所学习的特征表示在后一阶段并未得到充分利用，因此，文献［19，27］对特征进行跨阶段的传递，实现对高维特征域信息的维护，文献［17-18］提出特征域优化思想，利用特征域梯度下降算法实现信息的更新，取得较好的重构性能。

通过对大量优化启发工作进行分析发现，这类算法性能的增益很大程度归功于每个阶段的梯度下降过程，表明了梯度学习对于高精度图像重构的重要性。然而，现有的优化启发工作在每阶段的更新过程中仅学习单一梯度，存在一定的不足：①每阶段的梯度信息实际上是图像信号的残差信息，每阶段仅学习单维的残差信息是不充分的，这意味着更高精度的重构性能需要更多的优化阶段来取得；②单维梯度的学习容错性不强，学习过程容易不稳定，导致模型训练收敛较慢；③每阶段仅学习单一梯度，表征的信息有限，模型的泛化能力较弱。

受经典的Bagging算法［28］启发，本研究提出高维空间梯度学习算法，实现一种由多维弱梯度学习器组成强梯度学习器的理念。一方面，所提算法通过学习多种不同的梯度，更充分地挖掘每阶段重构信号与真实测量值之间的残差信息，恢复更多的图像细节；另一方面，相比于单维梯度，算法的多维梯度空间能够容纳不同的梯度，同时允许某些维度上噪声的存在，因此可以得到泛化性及容错性更强的梯度表示。此外，在模型学习的过程中，学习梯度由单维度转变为多维度支撑，梯度的学习难度被分摊到多维度上，减轻了梯度学习的负担，获得更快的模型训练收敛速度。结合近端梯度下降算法［24］及特征域优化思想［17］，本文提出特征域近端高维梯度下降（FPHGD）算法，并利用该算法设计实现特征域近端高维梯度下降网络（FPHGD-Net）。此外，本文还对不同复杂度的深度空间近端映射结构进行开发，以适用于不同应用场景。根据模型的时间及空间复杂度从低到高，设计的模型依次称为FPHGD-Net-tiny、FPHGD-Net、FPHGD-Net-Plus。

1 优化启发图像压缩感知重构网络

1.1 近端梯度下降算法

在图像压缩感知重构中，利用测量值y重构原始图像信号x是一个经典的病态逆问题，该问题可以通过对稀疏正则项的l1范数进行约束，从而将非凸的组合优化问题转化为凸优化问题进行求解，相应的优化模型如下所示：

式中，λ为正则项系数，Ψ为图像信号的稀疏变换矩阵。式（2）通常采用近端梯度下降（PGD）算法求解，该算法的每一次迭代过程由梯度下降及近端映射算子组成，以实现迭代过程中对原始信号的逼近。假设k-1为当前已完成的迭代次数，第k次优化过程表示为

式中，ρ为梯度下降步长。式（3）为梯度下降过程，式（4）为近端映射过程。

1.2 基于优化启发的图像压缩感知重构网络

迭代收缩阈值算法（ISTA）利用软阈值处理实现近端梯度下降算法中近端映射过程的求解。通过建立迭代收缩阈值算法到深度重构网络优化阶段之间的映射，ISTA-Net［10］能够以数据驱动的方式学习模型的优化参数表示，例如稀疏变换系数，梯度下降步长等，相比于人工设置参数，该方式能够得到更优的参数表示，同时仅需少量的迭代次数就能取得更好的重构性能。

在ISTA-Net中，rk子模块及xk子模块被分别用于模拟式（3）与式（4）的计算过程，相应模块数学式表示如下：

式（5）表示ISTA-Net的梯度下降过程，计算过程与式（3）一致；ISTA-Net在高维特征空间利用软阈值收缩对式（4）进行求解，求解过程如式（6）所示。在式（6）中，soft(·)运算表示软阈值处理，Θ为可学习的收缩阈值，变换函数F(·)与F͂(·)均由卷积网络构造，用以学习拟合图像信号的稀疏变换对。ISTA-Net能够具有较强的可解释性的同时，通过数据驱动的方式学习泛化性能更强的模型。然而ISTA-Net简单的设计架构未能充分发挥深度网络的特征学习和特征处理能力，后续的许多工作通过采取更复杂的网络架构（如多尺度网络［19-20，22］、Transformer架构［21］）或从信息的优化角度［14-15，17，23］上进行改进以进一步提升重构性能，大量的工作均表明了利用传统优化算法指导重构网络设计的可行性。

2 FHPGD算法及其网络实现

基于优化启发的重构网络取得高精度重构性能的关键技术之一在于每阶段学习重构信号与真实测量值之间的残差信息，即重构网络实现梯度下降的过程，然而从信息获取的角度上分析，现有的工作在每阶段仅学习单个梯度，未能充分发挥深度网络学习信息的能力，信息学习不足不利于图像信号的重构，此外，仅在单一维度上进行梯度学习，难以学习到准确的梯度表示，造成不稳定的模型训练。因此，本文中提出了特征域近端高维梯度下降（FPHGD）算法。在本节中，将首先详细描述本文提出的FPHGD算法，然后给出基于FPHGD算法设计的特征域近端高维梯度下降网络（FPHGD-Net）的框图和实现细节。

2.1 特征域近端高维梯度下降算法

与大多数图像压缩感知重构（ICS）网络不同，本文提出的算法优化对象为特征域信息Xf。假设在第k阶段优化过程，输入为前一阶段已完成更新的特征Xk-1f，由于测量值y在原始图像域上通过测量获得，因此一般的做法通过反变换函数将Xk-1f反变换至图像域作进一步的梯度计算，过程如下：

式中，δk为第k阶段优化过程产生的单维梯度。

需要指出，上述的学习过程极具挑战性，因为难以通过反变换函数对高维特征域中涵盖的所有有用信息进行组合，并压缩至单维的图像域进行充分的表示。本文中提出的高维空间梯度学习算法能够有效缓解梯度学习的压力并更充分地完成梯度信息的学习。在所提算法的高维梯度学习空间中，每个维度均可以看作单维弱梯度学习器，由多维弱梯度学习器组成强梯度学习器，实现更准确、更充分的梯度学习。因此，与现有的工作不同，本文算法的反变换函数组成，其中M为梯度学习维度的数量。通过组合不同的子变换函数，原有的特征能够更充分的被表示；此外，原本学习变换函数的难度被分摊到不同的上，减轻了网络学习具有强泛化能力的反变换函数的负担。通过利用多核反变换函数，图像的高维特征空间表示Xfk-1被反变换至图像域集合Xik，其中Xik由{xk1，xk2，…，xkm，…，xkM}组成，xkm表示第k阶段每一维度的输出子图像。需要指出，不同的xkm之间即存在着交集也存在着差异性，这种差异性使得在学习高维梯度的过程中，能够得到不同的梯度，从而更充分地挖掘隐含在测量值中的残差信息，解决了以往仅学习单一梯度的弊端。为了输出高维的梯度，测量值y需拓展至与Xki具有相同维度的Y，从而可以将式（7）的单维梯度计算过程转化为如下所示的高维梯度计算过程：

式中，Δki={δ1k，δ2k，…，δmk，…，δMk}表示高维梯度，δmk为每一维度输出的“弱”梯度，Φ与ΦT独立的作用在Xik的每一维度以获得多个不同的梯度。

为了能够对前一阶段学习得到的高维特征进行保留，受文献［17］特征域优化思想启发，本文在特征域中实现高维梯度下降过程。需要指出，在实现到特征域的映射过程中，变换函数F(·)实现不同梯度信息的组合，以回归得到更准确的特征域梯度。特征域梯度下降过程如下：

为了充分发挥深度网络的学习能力，本文利用图像的高维特征空间表示Xf具有的先验信息，在特征域上直接完成近端映射算子的求解，而无需经过图像域与特征域之间的转换过程。特征域近端映射算子如下式：

完整的ICS特征域近端高维梯度下降（FPHGD）算法描述如下：

算法：输入：输出：参数：123456789特征域近端高维梯度下降算法测量矩阵Φ、测量值y重构图像x迭代次数K、梯度学习维度M、特征维度C梯度下降步长ρ、正则项系数λ xi ← ΦTy//图像的初始重构Y ← Repeat(y，M)//对测量值进行M次重复拓展X0f ← f(xi，C)//将图像映射至特征域while(k≤K)： // k初始值为1 Xki ← F͂k(Xk-1 f，M)//生成图像域集合Δki ← ΦT(ΦXk i-Y)//计算高维梯度i，C)//多维梯度组合映射Uk ← Xk-1 Δkf ← F(Δk f-ρΔk f//特征域梯度下降Xkf ← arg min Xf 12‖Xf-Uk2 2+λ‖‖Xf1//特征域‖10 11近端映射k ← k+1 x ← f͂(Xk f)//高维特征反映射至图像域输出

在下一小节中，将详细介绍基于FPHGD算法设计的特征域近端高维梯度下降网络FPHGD-Net。

2.2 特征域近端高维梯度下降网络

根据特征域近端高维梯度下降（FPHGD）算法设计的特征域近端高维梯度下降网络（FPHGD-Net）整体框架如图1所示。FPHGD-Net整体架构由卷积神经网络实现，并由编码器及解码器两部分组成。在功能实现方面，编码器负责对图像信号进行线性采样及压缩，解码器利用编码器产生的低维测量值高精度地重构原始图像。在编码器中，测量矩阵对原始图像信号进行线性测量，输出低维测量值y；在解码器中，首先对测量值y进行线性逆映射，以得到初始重构图像xinit，随后将xinit映射至特征域并进行多阶段的迭代，以获得更好的细节恢复。接下来，将介绍FPHGD-Net各部分的设计，并详细讨论FPHGD-Net优化阶段的实现。

图1 特征域近端高维梯度下降网络整体框架Fig.1 Overall framework of feature-domain high-dimensional gradient descent network

2.2.1 特征域近端高维梯度下降网络

应用压缩感知理论的主要优点之一在于编码器能够以低复杂度的计算完成信号采样，同时实现对信号压缩。为了遵循编码器低复杂度的设计原则，并使解码器能够高精度地解码出原始图像信号，与先前的工作类似［6］，本文采用可学习的采样矩阵代替固定的随机高斯矩阵进行非重叠分块采样（BCS），实现编码器和解码器的联合优化。在这里，给定原始图像信号x∈RH×W，图像块大小为B×B（不满足整除条件的图像块边界用零填充），卷积张量WΦ∈RM×1×B×B，卷积步长设置为B×B，编码器的线性测量过程如下：

式中，编码器输出测量值y∈RrB2×1×(HB)×(WB)，采样率r=M/B2，*为卷积运算符号，SΦ(·)在本文中定义为线性测量算子。

2.2.2 FPHGD-Net解码器初始重构网络

为了更好地利用图像先验信息帮助图像细节的恢复，在进行深度重构之前，需要实现图像信号的初始重构。若额外使用卷积张量完成信号的初始重构将引入B2×M大小的参数量，这对模型参数不友好。与传统的优化算法类似，本文采用测量矩阵的转置形式来完成图像信号的初始重构，这样的好处是即能够得到合理的初始估计，同时能够充分地利用采样矩阵。为了得到转置矩阵，卷积张量WΦ被重塑为B2个大小为M×1×1的卷积滤波器，通过该方式可以得到大小为B2×M×1×1的转置卷积张量WΦT。由于利用WΦT对测量值y进行步长为1的卷积产生的输出为1×B2×(HB)×(HB)大小的张量，为了得到与原图大小一致的初始重构图像，本文采用Pixelshuffle［29］操作重塑输出张量。信号初始重构过程如下：

式中，SΦT(·)在本文中定义为转置线性测量算子。

2.2.3 FPHGD-Net深度恢复子网络

深度恢复子网络的作用在于对初始重构的图像进行深层次的细节恢复，本文设计的深度恢复子网络是FPHGD算法的反映，其整体架构如图1解码器部分所示。在该子网络中，初始重构图像xinit首先经过非线性变换函数f(·)映射至高维的特征域获得初始的特征表示X0f，其中f(·)由一个卷积层及残差块组成，卷积层用于将图像信号映射至高维空间，残差块用于对信号产生非线性映射；然后，特征X0f经过多阶段的迭代优化，每个优化阶段对应于FPHGD算法的一次迭代过程，信息的优化保持在特征域内实现；最终，最后一次迭代的输出结果经过非线性逆变换函数f͂(·)反变换至图像域，并输出重构图像xrec，其中f͂(·)在结构设计上与f(·)对称，以更好地模拟变换的互逆性。根据FPHGD算法的实现过程，将网络的每个优化阶段细分为两个优化子阶段：特征域高维梯度下降以及深度空间近端映射。在本文中，设计了特征域高维梯度下降模块（FHGDM）以及深度空间近端映射模块（DPMM）进行上述两个子阶段的实现，相应的模块设计如图2（a）及图2（b）所示。

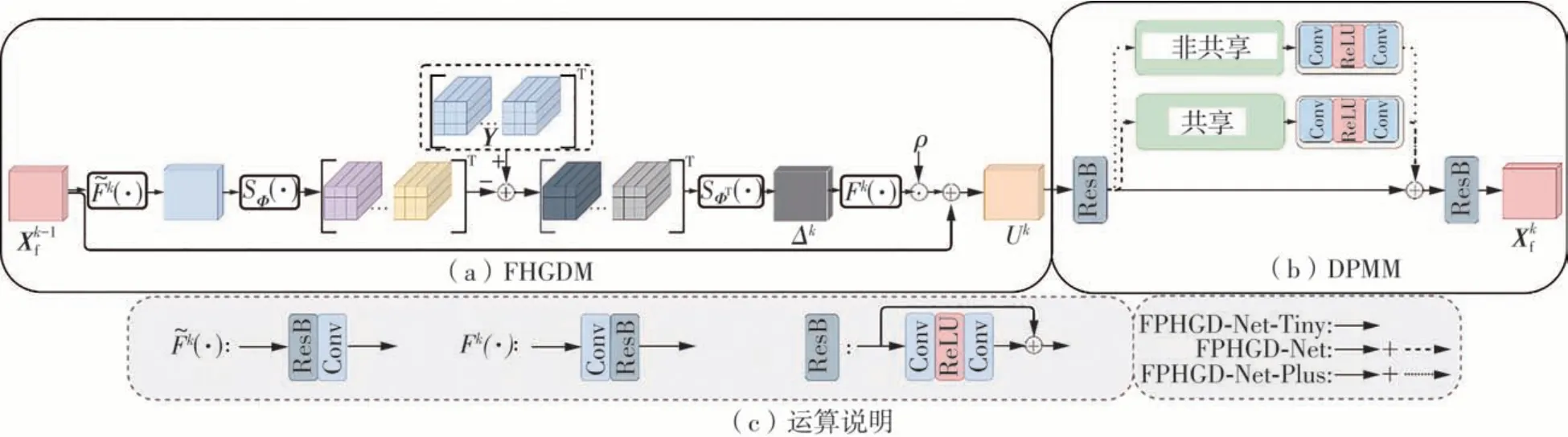
图2 特征域近端高维梯度下降网络优化阶段结构Fig.2 Optimization phase structure of feature-domain high-dimensional gradient descent network

（1）特征域高维梯度下降模块

特征域高维梯度下降模块（FHGDM）是对FPHGD算法中式（8）-（10）的反映，其设计遵循了高维空间梯度学习与特征域梯度下降的思想。为了满足这样的设计理念，算法的变换函数Fk(·)与需满足以下设计原则：①Fk(·)与在结构上需保持对称式的设计，以更好的对变换可逆性进行模拟；②Fk(·)与设计上需具备多个不同的卷积核，不同的核用于不同维度的梯度学习，以满足高维空间梯度学习思想的要求；③由于Fk(·)对高维梯度产生非线性映射的过程中，需要对M维梯度的信息进行组合，因此Fk(·)中卷积核大小需设置为M×P×Q，其中M为梯度学习的维度数量，P×Q表示单维度上卷积区域的大小。

本文设计的特征域高维梯度下降模块如图2（a）所示。在该模块中，首先，前一阶段的特征Xk-1f经过反变换函数输出图像域集合Xik；在得到图像域集合Xik后，利用测量算子SΦ(·)对Xik的每一维子图像进行独立地测量；随后，将产生的多维测量结果与重复拓展得到的多维测量值Y作差，并将得到的差值利用转置测量算子SΦT(·)进行反映射得到高维梯度Δki；然后，变换函数Fk(·)对Δki中的多维梯度进行信息组合并映射至特征域，从而获得特征域梯度；最后，跳跃连接用于构造前一阶段的输出特征与特征域梯度的连接通道，以实现信息在特征域的梯度下降过程。在模块设计中，变换函数Fk(·)与均由卷积层与残差块构成。需要指出，Fk(·)的实现与变换函数f(·)不同，在Fk(·)的卷积层中卷积核大小为M×3×3，用于组合M维梯度信息，此外，的实现也与变换函数不同，的卷积层由多个卷积核来实现，这样的好处是能够通过极简单的构造方式建立变换函数集合并且能够使得每个子变换函数均与变换函数f(·)在结构上满足对称的关系。上述的优化过程如下：

（2）不同复杂度的深度空间近端映射模块

求解近端映射过程可看作图像信号的去噪处理，常用方法为软阈值处理，然而基于稀疏性先验的软阈值去噪的方式，难以建模重构过程中复杂的噪声。本文采用残差网络［30］，实现式（11）的求解。模块设计如图2（b）所示，考虑到现实中对重构速度的追求，本文采用两个级联的残差块实现信号噪声的二次去除。假设Uk=Xf+E，其中E为信号的干扰项，使用残差结构的好处是，卷积支路能够以非线性的方式拟合特征的噪声，残差分支能够对原有特征进行保留，因此使用残差网络D(·)的去噪过程表示如下：

得益于本文提出算法的优越性，尽管上述方法在基于深度学习去噪算法中是一种相对简单的去噪处理，但实现的模型在保持速度优势的同时，也能够取得优异的图像重构性能，因此把这种具有快速且具有较高精度重构性能的特征域近端高维梯度下降网络称为FPHGD-Net-Tiny。

为了进一步提升模型的重构性能，本文采用U型网络实现不同尺度的特征提取，该网络结构如图3所示。使用U型网络可以扩大卷积网络的感受野，实现对更大范围信息的捕捉与建模，然而该结构的引入会导致模型参数量急剧上升，虽然采取对所有阶段的U型网络参数共享能够有效的减少模型参数，实现解码器的参数友好，然而这对每个阶段的细节恢复缺乏灵活性。因此本文采取部分共享的策略，如图2（b）所示，通过给共享的U型网络搭配非共享的小型非线性网络，并采取残差式的构造实现更好的特征细节恢复，在卷积分支上，非共享小型网络能够利用U型网络提取到的丰富特征，生成用于细节恢复的残差信息，使得模型既能具备参数友好的优势，同时又能较灵活完成细节的恢复，因此把这种参数友好并且具有高精度重构性能的特征域近端高维梯度下降网络称为FPHGD-Net。此外，为了取得更高精度重构性能的网络，本文也对非共享U型网络进行了实现，相应的模型称为FPHGD-Net-Plus。

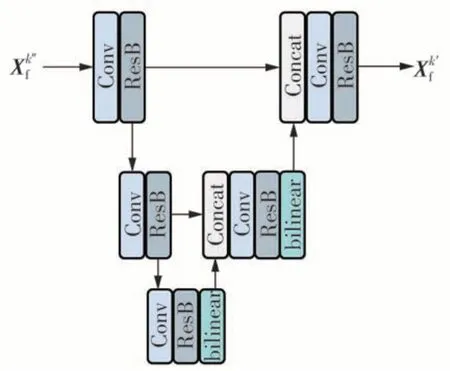
图3 U型结构Fig.3 U-shape structure

2.2.4 损失函数

对于原始输入图像x∈RH×W，深度重构网络的输出记为xrec，本文采用最小化均方误差对模型的输入与输出执行端到端的约束：

为了减少信息的冗余采样，本文与文献［11］类似，对采样矩阵采取正交性约束作为模型训练的辅助损失函数：

需要指出，本文不对变换Fk(·)与施加可逆性约束。这样的好处是不对模型的学习空间进行限制，能够更充分的发挥模型学习表示的能力；此外，很重要的一点，在本文提出的算法中，Fk(·)除了学习信号到特征域的非线性映射外，还需要学习对多维梯度信息组合的能力，因此，在严格意义上，Fk与并不完全满足可逆性质。特征域高维梯度下降网络总的损失函数为

式中，γ为辅助损失函数的权重因子，在本文模型中γ被设置为0.2。

3 实验仿真与分析

3.1 模型实现细节

（1）训练数据集。与文献［6］类似，本文选取广泛使用的BSD400［31］数据集（共400张图象）作为模型FPHGD-Net-Tiny和FPHGD-Net的训练集。出于对使用小数据集训练大模型容易导致过拟合的考虑，对于FPHGD-Net-Plus模型，增加了DIV2K［32］数据集（共800张训练集图像）用于模型的训练。训练完成的模型分别在Set11［4］数据集、BSD68［31］数据集以及Urban100［33］数据集上进行测试，测试评价指标为峰值信噪比（PSNR）以及结构相似度（SSIM）。

（2）本文模型设置。本文设计的3种模型，除U型结构部分外，模型的特征通道数C均设置为16；U型网络尺度数S设置为3，该网络结构由上到下特征通道数分别设置为C、2C、4C；为了避免通道压缩造成的信息损失，梯度学习维度M设置为16；由于梯度下降步长ρ是一个线性比例系数，而这种比例关系在训练过程中能够被卷积网络进行学习，因此在本文中梯度下降步长ρ设置为1；FPHGD-Net-Tiny的网络优化阶段数k设置为16，考虑到模型的推理速度，FPHGD-Net和FPHGD-Net-Plus网络优化阶段数k设置为12，以实现快速高性能的推理。

（3）模型训练细节。训练的输入数据被随机裁剪为96×96大小的子图像，彩色的子图像转换为YCbCr格式并仅利用Y分量进行模型的训练；训练采用随机翻转作为数据增强的策略；编码器非重叠块采样的分块大小B设置为32；训练采用AdamW［34］优化器，优化器权重衰减量设置为1×10-3；网络训练的Epoch数量设置为120，每个Epoch包含对训练集数据的300次迭代；模型初始学习率设置为2×10-4，并采用余弦退火学习率衰减策略对学习率衰减至1×10-5。所有实验均在GPU GTX1080ti的Pytorch平台上进行实现。

3.2 实验结果与分析

3.2.1 重构性能与视觉效果对比

（1）与现有算法重构性能对比

本文的主要贡献在于解码器算法的实现，为了实现公平的对比，本文选择的对比方法为近期前沿采用可学习采样矩阵的图像压缩感知重构算法，这些方法的编码器实现均与本文一致，包括：CSNet+［6］、NL-CSNet［7］、MR-CSGAN［8］、AMP-Net［15］、OPINE-Net+［11］、FSOINet［17］、MADUN［16］、DGUNet+［19］、DUDONet［23］、DPC-DUN［26］、LG-Net［22］。其中前3种为基于“黑盒”的重构网络，后8种为基于优化启发的重构网络，CSNet+、AMP-Net、OPINENet+、FSOINet、DGUNet+的测试由原作者发布的开源模型进行实现。为了验证本文算法的有效性，选取覆盖低采样率到高采样率的5种采样率即0.01、0.05、0.1、0.3、0.5进行相应模型的实现。

实验对比结果如表1所示，可以看出，基于优化启发的重构网络总体上要优于“黑盒”网络，采样率越高，优势越明显，这是因为在高采样率下测量值所隐含的信息量增多，充分挖掘测量值信息对细节恢复起到更重要的作用。本文提出的特征域高维梯度下降网络FPHGD-Net的PSNR，相较于近端梯度下降算法设计的OPINE-Net+在Set11数据集的5个采样率上分别具有2.1、1.52、1.19、1.5、1.23 dB的提升，相较于基于特征域优化思想的FSOINet平均有0.45 dB的性能提升；值得注意的是，本文的小型网络FPHGD-Net-Tiny能够以简单的架构取得优于绝大多数算法的重构性能，证明了本文算法设计的有效性；本文的增强版FPHGDNet-Plus，在增加一定的参数量及数据量后，能够表现出非常强大的性能。本文3种模型与OPINENet相比，在Setll数据上的平均PSNR分别提升1.34、1.51和1.88 dB，大程度优于对比算法。

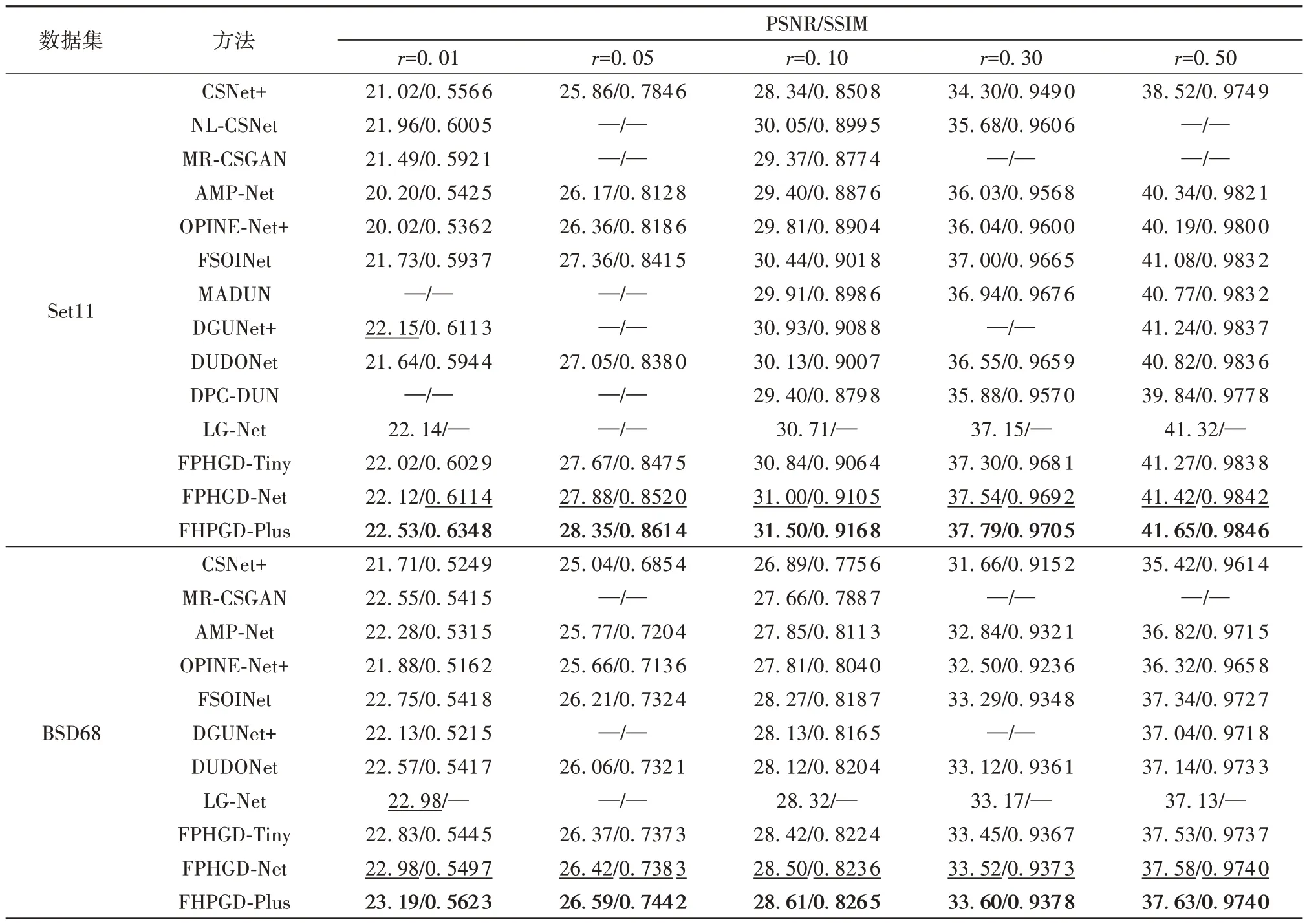
表1 不同算法在Set11数据集与BSD68数据集重构图像平均PSNR/SSIM对比1）Table 1 Average PSNR/SSIM comparison of reconstructed images on Set11 and BSD68 of different algorithms

（2）高清数据集泛化性能测试

本文选用具有较高分辨率的Urban100数据集作为模型泛化性能的测试集，测试结果如表2所示，由表中数据可以看到，本文提出的3种模型在总体上均优于其他参与比较的方法，其中模型FPHGDNet和FPHGD-Net-Plus的优势尤为明显，其原因在于模型通过建立多尺度网络从不同尺度上由粗到细对图像细节信息进行恢复，对于具有较高分辨率且纹理细节丰富的Urban100数据集来说能够取得更好的重构效果。相较于模型OPINE-Net+，本文的3种模型的PSNR在不同采样率下分别有0.81～1.52 dB、0.97～1.89 dB，1.67～2.66 dB的性能提升，与性能最好的模型DGUNet+相比，本文的模型平均PSNR有0.12、0.4、1.18 dB的提升，其中在0.5采样率下性能的提升尤为明显。

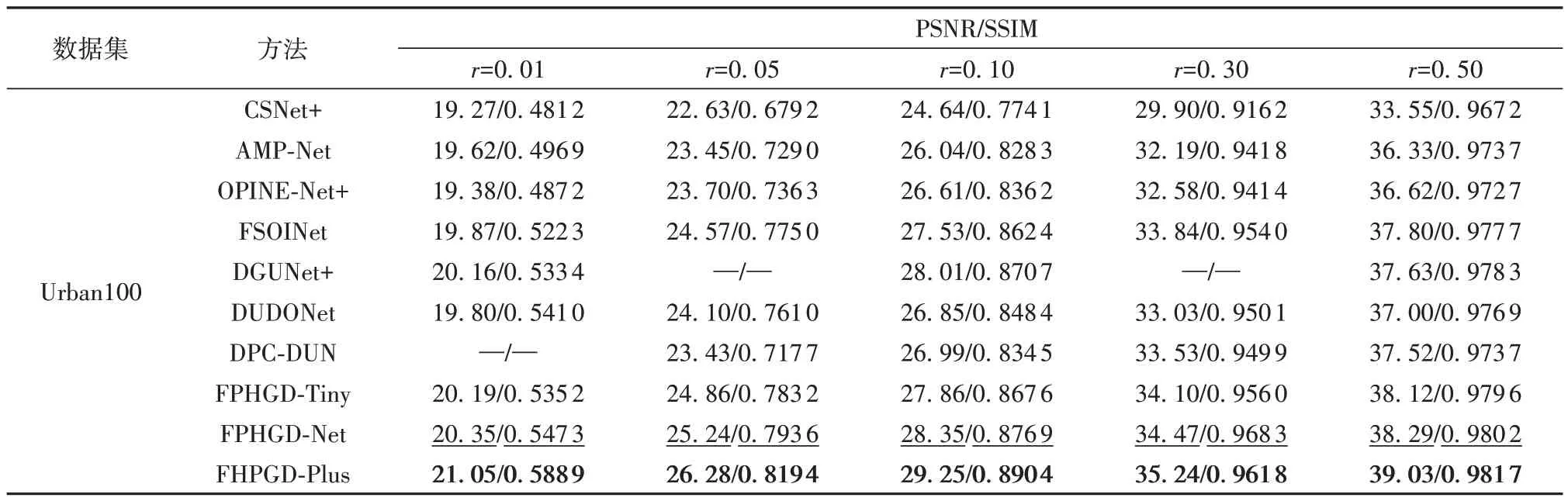
表2 在Urban100数据集的PSNR/SSIM泛化性能比较1）Table 2 Comparison of average PSNR/SSIM generalization performance on Urban100

（3）重构视觉效果对比

本文对比了不同算法图像恢复的视觉效果，定性的对模型进行分析。本文选取Set11数据集中细节信息丰富的Barbara图像作为0.1低采样率下的重构对比，以及Urban100数据集中含有丰富规则性纹理信息的现实场景Img098作为0.3较高采样率下的重构对比。对比结果分别如图4及图5所示。在0.1采样率下的Barbara图像，其他模型的恢复结果均具有明显的模糊效应，几乎看不到纹理细节，本文提出的模型能够恢复更多的纹理细节信息，FPHGD-Net及FPHGD-Net-Plus能够恢复出较清晰的细节边缘，FPHGD-Net-Plus模型能够产生与原图最为接近的恢复效果。从图5中可以看出，几乎所有的模型均在绿框砖块中产生了不同程度的模糊和错误的恢复，而本文的FPHGD-Net仍能够在某些细节区域得到较好的恢复，值得一提的是，本文的FPHGD-Net-Plus能够准确的恢复出大多数细节及清晰的砖块结构。

图4 采样率为0.1时Barbara（Set11）图像的重构视觉对比Fig.4 Reconstruction visual comparison of Barbara（Set11） at 0.1 cs ratio

图5 采样率为0.3时Img098（Urban100）图像的重构视觉对比Fig.5 Reconstruction visual comparison of Img098（Urban100） at 0.3 cs ratio

3.2.2 模型复杂度对比

本小节采取模型的参数量及推理时间分别对模型的空间复杂度以及时间复杂度进行评估，其中空间复杂度以0.5采样率下模型的参数量为准，时间复杂度由模型在BSD68数据集上的平均推理时间来评估。为了对比的公平性，仅与开源模型在同平台上进行算法复杂度的比较。比较结果如表3所示，结合表1可以看出，通过采取参数部分共享策略，本文的模型FPHGD-Net能够在参数量上优于其他模型，同时能够保持优于其他算法的重构性能，表明了该策略下，模型的参数可以被更充分的利用。值得注意的是，本文的模型FPHGD-Net-Tiny具有最少的参数和仅次于OPINE-Net+的重构时间，同时FPHGDNet-Tiny总体重构性能也优于其他算法，充分表明了该模型的轻量性以及本文算法设计的高效性。

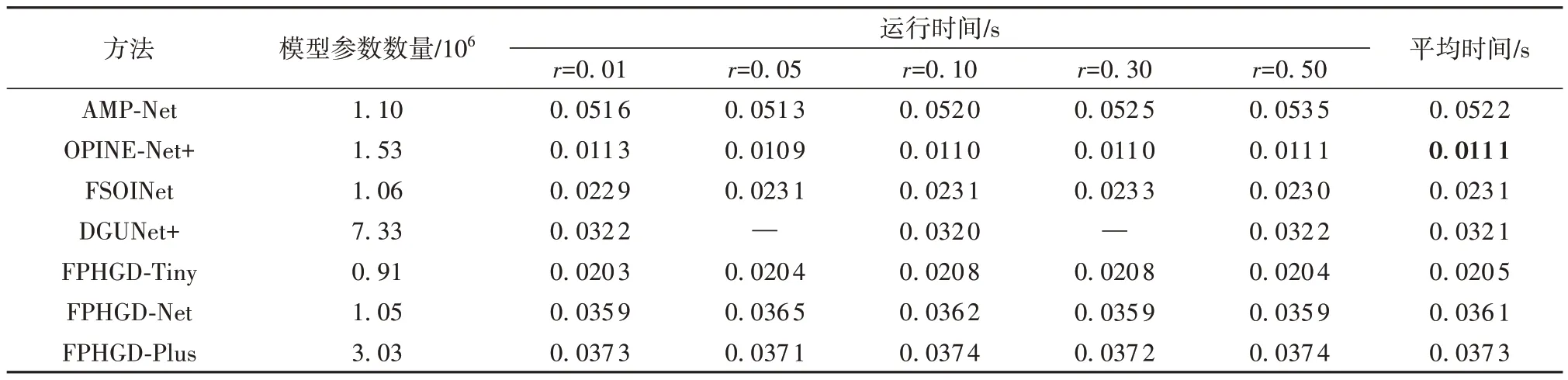
表3 模型时间及空间复杂度对比（BSD68数据集，GPU1080 Ti）Table 3 Comparison of time and space complexity （BSD68， GPU1080 Ti）

3.2.3 模型的消融实验与分析

在这一小节中，将对不同的模型设计进行研究分析，其中包括特征域近端高维梯度下降算法以及深度空间近端映射模块中参数共享策略。实验条件与3.1节设置相同， 实验采样率设置为0.3。

特征域近端高维梯度下降算法的消融研究主要包括3个部分：近端梯度下降（PGD）算法、特征域优化（FDO）思想，以及高维空间梯度学习（HDG）思想。在该研究中，模型优化阶段数量均设置为16，实验过程通过调整残差块的数量使得不同设置下参数尽量一致，其中Base模型由级联残差块构成，实验设置及结果如表4所示，设置①和③在使用相同去噪网络的情况下，通过增加fk(·)与f͂k(·)单维映射的复杂性实现相对公平的对比，设计①相较于纯残差结构网络，引入PGD算法能够带来大幅度的性能提升，表明基于优化启发的网络设计的有效性；设计②将PGD算法和HDG思想相结合，该设计可看作近端高维梯度下降（PHGD）网络，相较于设计①，性能得到进一步的提升，表明高维梯度学习算法能够更有效地挖掘测量值信息，实现更好的图像恢复效果；设计③将PGD算法与FDO思想相结合，该设计可看作特征域近端梯度下降（FPGD）网络，相较于设计①，性能得到进一步的提升，表明运用特征域优化思想能够更有效地完成信息的优化；设计④为特征域近端高维梯度下降（FPHGD）网络，相比于其他设计，其性能的增益最大，表明了该算法能够更充分地对信息进行挖掘，同时更有效地完成信息的优化，实现更高精度的图像恢复效果。

表4 特征域近端高维梯度下降算法消融研究Table 4 Ablation of feature-domain proximal high-dimensional gradient descent algorithm

深度空间近端映射模块参数共享策略的研究在FPHGD-Net-tiny模型基础上进行实现，模型优化阶段数量设置为12。该研究内容包括共享U型网络、共享U型网络+非共享小型网络、非共享U型网络+非共享小型网络。实现过程中通过合理设置残差块的数量以保证模型参数量尽可能接近。实验结果如表5所示，可以看出，相比于基础网络，使用共享U型网络在Set11数据集与Urban100数据集上均有大于0.2 dB性能的提升，说明多尺度网络有益于图像的恢复。给共享的U型网络搭配非共享的小型网络，相比于仅共享U型网络，性能平均提升0.12 dB，不灵活的细节恢复得到了一定的缓解。值得注意的是，均非共享的网络性能稍低于共享U型网络+非共享小型网络，这是因为在小数据集上，大模型难以得到充分的优化而导致。

表5 深度空间近端映射共享策略消融研究Table 5 Ablation of deep-space proximal mapping sharing strategy

4 结论

针对过去基于优化启发的图像压缩感知重构工作仅学习单梯度的不足，本文提出了高维空间梯度学习思想。在此基础上，本文提出特征域近端高维梯度下降算法，并利用该算法成功设计了特征域近端高维梯度下降网络FPHGD-Net，实现高精度的图像恢复效果。同时，本文还对不同的深度空间近端映射网络结构进行了实现，以满足实际过程中不同的硬件需求。实验结果表明，与现有的工作相比，本文提出模型的重构性能更优，并能够对图像细节进行更好的恢复。往后，将基于本文提出算法的思想，进一步拓展至其他图像恢复以及视频压缩感知重构任务中。