衍生高效用模式挖掘算法综述

刘淑娟 韩萌 高智慧 穆栋梁 李昂

摘要：在数据挖掘领域中，高效用模式挖掘任务具有较高的理论研究价值和广泛的实际应用场景。针对多变的应用场合，提出了一系列衍生高效用模式。首先从关键技术的角度对高平均效用模式挖掘算法进行了分类论述，主要包括基于先验、基于树、基于列表、基于投影和基于数据格式的方法。其次，分析讨论了基于全集、精简集以及融合模式的含有负效用的高效用模式挖掘算法。再次，从模糊高效用模式、相关高效用模式和其他新兴高效用模式三个方面概述和总结了扩展高效用模式算法。最后，针对现阶段研究方向的不足，给出下一步的研究方向。

关键词：衍生高效用模式；高平均效用模式；负效用；模糊高效用模式；相关高效用模式；综述

中图分类号： TP311.13文献标识码： ADOI：10.3969/j.issn.1007-791X.2024.02.005

0引言

频繁模式挖掘[1]（Frequent Pattern Mining， FPM）假设数据库中所有项目具有相同的重要性，主要通过其二进制属性（该项目是否在事务中出现）从数据库中寻找频繁发生的项集。然而，现实生活中，特别是在市场数据库中，每条事务都包含了项目的内在价值，因此仅考虑项集的频率对于找出高利润的项集意义不大。例如，{香烟，红酒}是一个频繁项集，这仅体现了香烟常与红酒同时销售，并未体现其数量和价值信息。为解决其局限性，提出了高效用模式挖掘[2]（High Utility Pattern Mining， HUPM）， 通过定义项目的单位利润和数量来发现具有高效用（如产生高利润）的项集。例如，{香烟：2， 红酒：1， 纸巾：1}表示顾客购买2包香烟、1瓶红酒和1包纸巾，以上单件商品利润分别为25元、200元和1元。经计算，此项集产生251元的利润，销售者可根据自身制定的标准来判断此项集是否为一个高效用项集（High Utility Itemsets， HUIs）。在购物篮数据分析中，这能有效帮助决策者制定营销计划。

尽管HUPM通过考虑效用度量揭示了有意义的高效用模式，由于实际应用的多变性，面对复杂的需求，传统的HUPM无法普遍适用于多元化的生活场景。针对特定某一类问题，研究者们提出了更加精确的解决方案。于是，以高效用模式為基础，衍生出一系列较为复杂的模式。传统HUPM忽略了项集长度对效用值的影响[3-4]，因此会产生大量无意义的长模式，即长项集中可能会包含大量低于效用平均值的项。例如，销售者将利润高于200元的商品称为HUIs，由于红酒利润较高，故其与任意商品组合均为HUIs，如{红酒，纸巾}、{红酒，纸巾，尿布，口香糖，…}等，即使HUIs中存在如纸巾这样的低利润项，但项集的利润随着物品组合数的增加而增加，此时，效用度量更偏向于长项集。为解决此问题，TPAU[3-4]算法引入平均效用度量以挖掘高平均效用项集（High Average Utility Itemsets，HAUIs），即单位效用较高的项集，首次提出高平均效用模式挖掘（High Average Utility Pattern Mining， HAUPM）方法删除大量长度较长但含有低利润项的HUIs。由于其具有两阶段算法[5]的局限性，随后PBAU[6]算法采用投影技术缩小数据库规模。HAUP-growth[7]算法通过树结构存储信息减少数据库扫描次数。HAUI-Miner[8]算法设计紧凑的垂直列表结构高效挖掘HAUIs。为提高挖掘效率，MHAI[9]算法和FHAUI[10]等算法通过设计紧凑上界来减少候选项集数量，进一步丰富该模式领域。

此外，HUPM的局限性还在于未考虑项效用为负的情况[11]。实际上，负项存在于生活的方方面面，如商家的销售亏损和消费者的欠费行为等，例如，香烟降价促销，出现亏本的情况，其利润为-1元，即亏损1元处理，但商家可通过将香烟红酒捆绑销售的策略保证收益为正。由于HUPM的方法仅考虑了项效用为正的情况，则无法直接应用于负项存在的场景。HUINIV-Mine[12]算法首次引入了负效用的概念并挖掘含有负项的高效用模式，克服了HUPM仅适用于正项的局限。随后，人们还研究了其它问题，如基于Top-k的TopHUI[13]算法、增量数据库上的HUPM算法ITPAU[14]、数据流上的HUPM算法HND以及不确定数据库上的HUPNU[16]算法等，使得模式挖掘的任务进一步广泛应用。

近年来，学者们仍致力于对高效用模式的创新研究工作。一些新兴的衍生HUPM方法逐渐出现在大众视线，如模糊高效用模式[17]、相关高效用模式[18]、占用高效用模式[19]和跨层级的高效用模式[20]等。针对传统高效用模式在定量数据库上挖掘会产生大量冗余项集的缺陷，HUFI-Miner[17]算法首次提出模糊高效用模式挖掘方法，引入模糊集概念，将难以表达的数量或利润关系转化为易于理解的语言表达。相关高效用模式挖掘任务解决了高效用模式挖掘结果中项集之间相关性较低的问题。Fournier-Viger等人[18]首次引入相关度量，同最小效用阈值共同约束挖掘过程，删减了大量项之间相关性较弱的模式。为进一步挖掘有用高效的模式，文献[19]结合效用和占用率概念，提出了占用高效用模式挖掘（High Utility Occupancy Pattern Mining， HUOPM）方法。通过比较模式和包含该模式的事务效用占比情况，判断该模式的重要程度以提取出更具代表性的有趣模式。此外，传统的高效用模式忽略了项目的分类信息，从而丢失了部分有意义信息，故跨层级的高效用模式[20]引入分类法概念，为模式中的每个项目设置相对应的类别。这种结合分类信息的模式发现为分析用户行为提供了新思路。

以上模式均衍生自高效用模式，故命名为衍生高效用模式；不同点在于针对特定问题提出的衍生高效用模式各有特点。此外，有学者研究了这些模式的融合以处理较复杂的问题。例如，红酒和纸巾的购买组合并不常见，故项目之间的相关性较弱，这种购买关系的推荐是无意义的。结合模式长度的影响，挖掘出单位利润较高的商品组合，Sethi等人提出CoHAI-Miner[21]算法挖掘相关高平均效用模式。此外，为克服现有HAUPM方法只能处理正效用的问题和在含负效用的数据库中模式发现不完全的局限，提出融合模式算法MHAUIPNU[22]挖掘含负效用的高平均效用模式。现阶段仍不断产生较为复杂的衍生高效用模式以处理传统高效用模式中存在的不足，模式之间可根据需求彼此结合更加精准地提供解决方案。为便于后续进一步研究和丰富内容，现总结分析衍生高效用模式挖掘的算法是必要且有意义的。本文将对以上模式的算法进行全面综述。

在现有的相关综述中，Singh等人[23]从数据结构的角度总结了带负项的高效用挖掘问题。随后，又从静态、动态和序列数据方面阐述并分析了HAUPM[24]算法的最新信息。张妮等人[25]首次从正负效用划分角度总结了HUPM算法。Almoqbily等人[26]根据时间顺序和算法采用的度量类型总结了相关高效用模式挖掘算法。以上文献仅对一类高效用模式算法进行介绍，此外，只简单涉及其余新兴高效用模式。李慕航等人[27]首次从高效用融合模式和衍生模式角度阐述归纳算法，但主要分析融合模式，仅涉及四种衍生模式，并未对近期新出现的高效用模式进行总结分析。

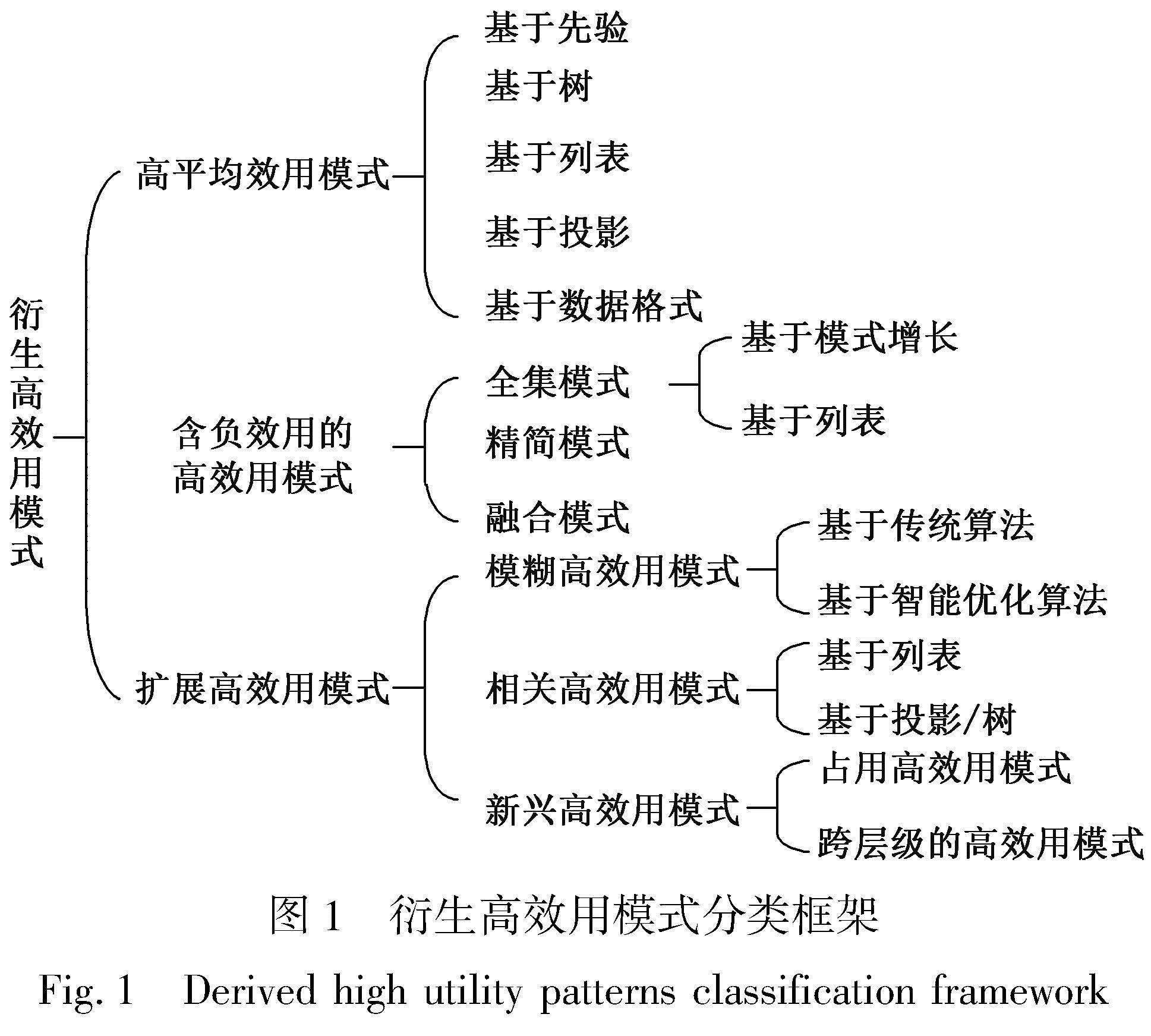
因此，本文从不同的角度切入，对多种衍生高效用模式进行全面分析总结并进行优缺点对比。衍生高效用模式分类框架如图1所示。本文贡献如下：

1） 全面总结了多种衍生高效用模式，包括高平均效用模式、含有负效用的高效用模式和最近提出的新兴高效用模式。

2） 首次从关键技术的角度对HAUPM算法进行分类总结和优缺点对比；从全集、精简集以及融合模式的角度对含有负效用模式进行分类总结和优缺点对比；最后，对扩展高效用模式挖掘算法进行分析归纳。

3） 根据目前研究不足，给出下一步研究方向，包括智能优化算法在衍生高效用模式挖掘中应用、结合项目分类法的跨层级模式挖掘和并行分布式挖掘等。

1相关概念和定义

为了清楚地描述部分衍生模式挖掘问题，给出一个事务数据库和一个效用表，如表1和表2所示。事务数据库是一组事务的集合，定义为D={T1，T2，…，Tn}，I={i1，i2，…，im}为一组项的集合，其中对于每个事务TC，TC∈I且具有唯一的标识TID。每一个项目i均有一个购买数量in（i，TC）（内部效用）和效用表（其中存储了项目到单位利润的映射）中项i的单位利润ex（i）（外部效用），即表1和表2中数字。

定义1（事务中的项/项集的效用）[2] 项i在事务TC中的效用记为u（i，TC），定义为u（i，TC）=in（i，TC）·ex（i）。项集X在事务TC中效用记为 u（X，TC），定义为

例：项A在事务T1中的效用为u（A，T1）=in（A，T1）·ex（A）=1×3=3。项集{AB}在事务T1中的效用为u（{AB}，T1）=u（A，T1）+u（B，T1）=13。

例：事务T2的效用tu（T2）=1×10+3×（－1）=7。

例：数据库中有6条事务， TU=tu（T1）+tu（T2）+tu（T3）+tu（T4）+tu（T5）+tu（T6）=84。

定义5（最小平均效用阈值）[2]δ∈[0，1]，最小平均效用阈值定义为minutil=δ·TU。

例： δ=0.7，minutil=0.7×84=58.8。

定义6（事务中项/项集的平均效用）[4]项i在事务TC中的平均效用记为au（i，TC），定义为au（i，TC）=u（i，TC）。

例：项集{AC}在事务T6中的平均效用为au（AC，T6）=2。

定义8（事务最大效用）[4]事务TC的最大效用记为tmu（TC），定义为tmu（TC）=max{u（i，TC）|i∈TC}。

例： tmu（T2）=max{u（A，T2），u（B，T2），u（C，T2），u（D，T2），u（E，T2）}=max{0，10，0，-3，0}=10。

定義10（高平均效用上限项集）[4]如果auub（X）≥minutil，项集X为高平均效用上限项集，记为HAUUBI。

定义11（高平均效用项集）[4]如果au（X）≥minutil，项集X为高平均效用项集，记为HAUI。

例： 设最小效用阈值minutil=10，

auub（{AC}）=tmu（T1）+tmu（T6）=10+10=20，

au（{AC}）=au（{AC}，T1）+au（{AC}，T6）=5.5，

auub（{AE}）=tmu（T5）+tmu（T6）=20+10=30，

au（{AE}）=au（{AE}，T5）+au（{AE}，T6）=13。

由定义10，项集{AC}和{AE}均为HAUUBI。由定义11，项集{AC}不是HAUI，{AE}是HAUI。

例： RTWU（{AE}）=RTU（T5）+RTU（T6）=57。

2高平均效用模式

由于项集的效用是项的效用之和，长项集会产生很高的利润，因此，传统HUPM倾向于寻找更长的项集，故在相同的阈值下，短模式不易被发现，其效用度量无法保证公平性。为解决HUPM的不足，HAUPM算法通过长度规范了项集的效用来发现单位效用较高的项集，因此删除了大量无意义的包含低效用项的高效用长模式。本节从关键技术对高平均效用模式挖掘的算法进行总结，包括基于先验、基于树、基于列表、基于投影和基于数据格式的方法。

2.1基于先验的方法

Apriori算法[30]是最早出现在关联规则挖掘中的算法，通过逐层水平迭代搜索的方式生成候选项集进而形成规则。其原理是利用Apriori性质，又称向下闭包属性（Downward Closure， DC） ，来限制候选项集产生来发现频繁项集，即若某个项集是频繁的，其所有的子集都是频繁的；若某个项集不是频繁的，其所有的超集也是非频繁的。随着用于克服FPM局限性的HUPM出现，Apriori性质也被用于效用挖掘中，如Two-phase算法[5]结合TWU模型和Apriori性质在两个阶段内挖掘HUIs。

然而，在效用挖掘中，项集的实际效用随着项数量的增加而增加。Hong等人首次在HUPM中引入平均效用概念并提出了一个两阶段挖掘算法TPAU[3-4]，算法利用auub度量高估项集的平均效用，筛选出auub值大于minutil的候选项集，通过再次扫描数据库计算候选项集的实际平均效用找到HAUIs。针对算法仅考虑单一最小效用阈值的局限性，HAUIM-MMAU[31]算法可为每个项目指定不同阈值，为挖掘具有多个最小效用阈值的HAUIs提供了一个基础框架，引入最小平均效用（Least Minimum Average Utility， LMAU）解决auub属性无法直接应用该框架的问题，并设计改进的估计效用共现剪枝（Improved Estimated Utility Co-occurrence Pruning， IEUCP） 策略和计算前剪枝策略（Pruning Before Calculation Strategy， PBCS）来尽早剪枝无希望的项集，从而加快HAUIs的发现。

当前的大部分 HUPM 或 HAUPM 算法均基于静态数据库，故不适用于动态数据的处理。 随后，ITPAU[14]算法引入快速更新（Fast Update， FUP）概念以处理增量数据挖掘的复杂情况，将新事务中挖掘出的新结果与原事务库中挖掘出的信息结合，通过重用部分有效信息来加速挖掘过程。但在某些情况下，该算法仍需重新扫描数据库来获取新的信息，知识维护的效率低下。Wu等人引入预大的概念来设置Sl和Su两个阈值以用于知识维护工作，并进一步提出APHAUIM[32]算法。该算法为避免多次扫描数据库，在缓存区内存储预大平均效用上限项集，因此节约了大量时间成本。

2.2基于树的方法

由于基于先验的算法需多次扫描数据库生成候选项集并验证，因此花费高昂的时空成本。故研究者们提出了基于树的挖掘算法，即通过数据库扫描构建存储项集相关内容信息的树[33]，随后挖掘过程中只需迭代遍历树而无需扫描数据库。

本小节将基于树的方法分为在静态数据上和在动态数据（增量数据、数据流）上的挖掘算法。

在静态数据上，Lin等人提出的HAUP-growth[7]算法中设计了新颖的压缩树结构HAUP-tree，树路径末端的每个节点存储项的auub以及路径中前项的数量，该结构结合模式增长方法导出模式。姜玫等人提出了一种不需要产生候选项集HAUI-Mine[34]算法，树中尾节点存有路径中的最大效用、路径中条件模式基的效用以及路径的效用列表。算法依据HAUI-Tree中的项，通过产生的条件模式基依次递归构建条件模式树以挖掘HAUIs。该算法的对比实验表明，在稀疏数据集上优于HAUP-growth算法。Lu等人[35]设计类似于索引表的项集结构以快速计算该项集的au和auub，并采用新的数据结构HAUI-Tree存储。该结构可根据项集属性直接计算出下一阶段中项集的效用值，提高了算法执行效率。

以上算法均基于静态数据库，由于现实应用程序中，数据往往以流的形式产生，数据库会随着事务的增加或删除而发生变化，此时，静态数据的挖掘方法将无法满足应用需求[33]。下面将总结动态数据上基于树的挖掘方法。

在增量数据库上，Kim等人提出IMHAUI[36]算法和新的数据结构IHAUI-Tree，IHAUI-tree上的每个结点N存储从根到N的路径重叠事务信息，通过结点的共享效应维护增量数据库的信息。Lin等人提出基于改进FUP概念的IHAUPM[37]算法以处理有事务插入的增量数据库，采用HAUP-Tree结构保存来自原始数据库的必要信息，将原始数据库和新添加的事务划分为四种情况进行维护。此外，该算法仅关注增量部分，利用部分内存就可以快速实现对HAUIs的更新。

在数据流上，姜玫等人提出一种不产生候选项集的挖掘算法ITR-Mine[34]，设计ITR-Tree结构维护窗口内数据信息，依次更新当前窗口内的数据并递归构建条件模式基和条件模式树，实现在数据流上的挖掘任务。SHAU[38]算法提出SHAU-Tree结构，其中每个结点用批量列表保存最近流数据中的平均效用信息以此挖掘最新的重要模式。此外，通过平均效用上界最小化剪枝策略提高算法的性能。由于最新数据可能比旧数据具有更高的影响，Yun等人首次应用平均效用因子和数据流衰减概念以处理敏感数据流上的事务，提出了基于阻尼窗口的MPM[39]算法，通过设计阻尼平均效用树（Damped Average utility Tree， DAT）维持事务的阻尼平均效用，为管理事务效用信息并确定无效事务，通过事务效用列表（Transaction Utility List， TUL）信息判断下一步候选验证。

HAOP-Miner[40]算法将HAUPM方法同一次性序列模式结合，采用反向填充策略计算支持度避免冗余节点的创建，此外，为解决枚举树生成大量候选模式，提出支持度下界方法并结合模式连接策略剪枝候选模式，从而实现了模式的高效剪枝。HANP-Miner[41]算法将HAUPM方法与非重叠序列模式挖掘结合，采用了基于简化Nettree结构的深度优先搜索和回溯策略计算模式的支持度，结合基于平均效用上限的模式连接策略减少候选模式的生成。

2.3基于列表的方法

由于先前已有的算法均需要大量计算来找到符合条件的项集。为此，研究人员还积极探索了基于列表的方法。效用列表结构内存占用较小且无需重复数据库扫描，此外，项集间的连接操作方便，k-项集（k>1）的列表结构可通过其子集的（k－1）列表结构连接操作构造。因此，受效用列表启发，HAUI-Miner[8]算法提出了平均效用列表（Average Utility List， AU-List）结构。与效用列表结构不同在于，三元组中剩余效用被替換为事务最大效用。该算法利用项集的平均效用与事务最大效用之和及早识别无希望项集。

为加快算法执行速度，解决上界松散问题， Yun等人提出MHAI[9]算法和新的数据结构HAI-List。在此基础上，设计了基于最大平均概念的预剪枝技术。FHAUI[10]算法提出了新颖列表结构IAU-List，该算法在首次数据库扫描后重新计算项集的tmu值以得到更加紧凑的平均效用上界。此外，引入估计平均效用共现剪枝结构 （Estimated Average Utility Co-occurrence Structure， EAUCS）减少项集间的比较连接次数。FHAUPM[42]算法提出一个较为松散的上界lubau，该上界在早期阶段有效淘汰候选项集，但当项集不相关时，性能提高不明显，随后，还引入更严格的上界tubau以缩小搜索空间。EHAUPM[43]算法开发了新的效用列表MAU-List结构，包含四元组（tid，iutil，rmu，remu），其中rmu为修正事务的最大效用，remu为事务剩余最大效用。在此基础上，引入lub和rtub两个更紧凑的上界。 TUB-HAUPM[44]算法应用两个新的更严格上界mfuub和krtmuub，同时对传统的全局事务上界进行改进，比较事务的两个上界值，选择较小值作为该事务上界实现快速紧化。LMHAUP[45]算法提出TA-List结构，其中，具有相同事务标识的元组在构造过程中相互链接以减少列表连接成本。此外，提出两个新的紧凑上界tmaub和mrau。

由于单一的最小阈值可能会导致项集过少或冗余的状况，且存在不公平因素，因此MEMU[46]算法利用多个最小效用阈值挖掘。为解决HAUIM-MMAU使用生成测试方式耗时的问题，该算法采用紧凑效用列表CAU-List和表示搜索空间的排序树挖掘HAUIs，根据列表中存储的rmu可快速得到rtub紧凑上界值。上述基于多最小阈值的算法均是按照最小平均效用阈值的升序处理项目以保留auub的DC特性，而传统HAUPM算法均是基于auub升序，因此不能直接采用HAUIM-MMAU和MEMU框架。针对此问题，GHAIM[47]算法引入后缀最小平均效用（Suffix Minimum Average Utility， SMAU）概念保持auub模型的DC特性和几种剪枝方法，使得所有修剪方法通用并且独立于项集的排序。

在增量数据库中，基于AU-List结构和FUP概念，Wu等人提出在事务插入更新时挖掘HAUIs的方法[48]，将原数据库和新事务中的HAUUBIs分为四种情况，更新数据集和AU-List，同时删除AU-List中的非HAUUBIs，从而有效维护HAUIs。FUP-HAUIMI[49]算法维护事务插入情况下的数据库，FUP-HAUIMD[50]是一种通过事务删除来更新发现的HAUP的算法。两者均引入改进版的FUP概念减少增量挖掘中候选模式数量， 仅在特定情况下进行原始数据库扫描。

随着研究的不断深入，HAUPM方法也同其它模式融合。Sethi等人将相关性度量引入HAUPM中，提出CoHAI-Miner[21]算法，使用垂直的列表结构保存效用和相关信息。通过与EHAUPM算法的实验分析对比，该算法能发现更多有意义的模式。MHAUIPNU[22]算法为挖掘具有正负效用的HAUIs，提出新颖数据结构TUBPNUL，引入严格上界tubpn并提出三种剪枝策略。

2.4基于投影的方法

在HAUPM中，投影技术和索引机制可加快算法执行速度，投影相关子数据库能有效缩小原始数据库的大小，从而只保留在挖掘过程中必要的项集信息，避免不必要的检查从而降低挖掘过程中的内存需求。

为了提高HAUPM的效率，Lan等人提出了PBAU[6]算法，该算法利用索引表结构模拟投影技术，投影当前前缀所需要的事务数据。随后，PAI[51]算法利用前缀映射方法，据项集持续变化更新投影事务的最大效用值以紧化上界。FIMHAUI[52]算法结合数据库投影和事务合并技术高效发现HAUIs，提出IHAUI-Tree结构的改进版本，仅在叶子结点中存储事务信息，用该结构來获取有希望项集的投影数据库，而无需生成条件模式基和局部树。

Thilagu等人提出一种基于平均效用的Web遍历模式挖掘算法[53]，该算法利用投影序列计算模式的事务加权效用，无需考虑整个序列中项的效用，这极大地减少了候选模式的数量。在不确定数据库中，李霆提出PrefixMUHAUSP[54]算法挖掘出高平均效用序列模式，通过投影数据库的方法，缩小数据库规模并生成更少的候选序列。

2.5基于数据格式的方法

为解决算法性能的不足，研究人员们提出了基于垂直数据结构和基于索引结构的挖掘算法。由于基于水平数据结构的挖掘方法需要额外的数据库扫描，HAUI-Miner算法设计了一种垂直表结构存储项集的效用信息，通过递归生成扩展项集的效用列表来提高挖掘速度。随后，在AU-list的基础上，许多算法引入更为紧凑的上界模型和剪枝策略，但仍花费大量时间成本浪费在评估不必要的模式上。

通常，研究者认为基于垂直表示法的上界与水平表示法（如auub和lub）相比表现良好。为解决

此外，基于索引结构的算法也可在一定程度上提高算法执行效率。类似于PBAU算法中使用的索引表，HAUI-Tree[35]算法中使用了一种特殊的项目结构快速计算项集效用，从而优化内存使用。EHAUI-Tree[57]算法利用索引表快速计算项集的平均效用上界，引入位数组结构保存项集信息，从而最大限度地减少内存的使用并提高计算效率。

2.6小结

本节首次将高平均效用模式挖掘方法按关键技术角度分类总结，分别为基于先验、基于树、基于列表、基于投影和基于数据格式的算法。如表3所示，从关键技术角度总结并对比了HAUPM算法。

本小结采用定量分析的方法在同一数据集上进行算法的时空消耗对比，并分析了此类方法的共同特点和仍普遍存在的缺陷。此外，对部分HAUPM算法的时间复杂度进行了分析比较。以TPAU[3-4]算法为代表，基于先验的算法采用生成和测试的方法挖掘，虽然剪枝策略能减少比较连接的次数和平均效用的计算成本，但仍需进行多次数据库扫描并在内存中生成大量候选项集，这极大影响了算法的时空效率；基于树的方法通过构建树结构存储原始数据库信息，在一定程度上克服了多次扫描数据库的弊端。在相同的最小阈值下，基于树的HAUP-growth[7]算法比TPAU算法快近一倍，但该算法内存消耗较大且随着树的高度的增长大大增加。此外，这类算法普遍存在的问题在于树的结构较为复杂且不利于算法扩展；基于列表的算法使用垂直压缩结构保留挖掘过程中所需信息，结构简单易实现。在Mushroom数据集上，当minutil为4%时，HAUP-Growth算法的执行时间为233.7 s，而基于列表结构的HAUI-Miner[8]算法仅需1.3 s，比HAUP-Growth算法快1～2个数量级，此外，在内存消耗方面同样优于HAUP-Growth算法，但这类算法的缺陷在于昂贵的列表比较和连接操作；基于投影的算法通过缩小原数据库规模减少扫描数据库的成本，例如PAI[51]算法，在BMS-POS和Chess数据集上，其生成的候选项数量远小于TPAU生成的，且运行速度比TPAU算法快得多。但其依赖于投影机制，在内存消耗方面不如HAUI-Miner算法。这类算法仍未克服生成大量候选项集的局限性；基于数据格式的算法主要指基于垂直数据结构的或者索引结构的挖掘方法，基于垂直数据库表示的算法在运行速度和列表连接次数方面性能较优，基于索引的方法在一定程度上提高了计算效率。在实验中，基于垂直挖掘的dHAUIM[55]算法比HAUI-Miner等算法快1～2个数量级，在Chess数据集上的实验结果显示，随着minutil的不断调整，该算法速度为HAUI-Miner算法的32～239倍。由于算法设计的上界比HAUI-Miner使用的传统auub上界模型更加严格，因此可在早期删除大量无希望的候选项来降低列表的连接次数。

此外，对部分HAUPM算法的时间复杂度进行了分析比较。ITPAU[14]算法是两阶段的算法，时间主要消耗在候选项集的生成和测试阶段，设Lk为生成k-项集的数量，kCi为i个元素组中k个元素的组合数，数据集中项的数量为n，则生成项集数为nC1+nC2+…+nCn=2n－1，故时间复杂度为O（2n）。基于树的IMHAUI[36]算法主要分为扫描数据库、插入新事务更新IHAUI-Tree、重构IHAUI-Tree、递归挖掘局部树等阶段。其中，设n是在新事务（n/2个不同项）插入之后，增量数据库具有的不同项数量。故扫描数据库以及更新树的时间复杂度为O（3n/2），该算法在挖掘过程中需按auub降序重构树，在使用冒泡排序调整路径的情况下，最坏时间复杂度为O（n2）。为n个结点构建局部条件树的时间复杂度为O（2np），其中p为参与构建局部条件树的结点个数，令Tz是z的局部树的递归模式增长操作时间。故整个挖掘过程

3含有负效用的高效用模式

传统高效用项集挖掘中，默认项的效用值为正。但在应用场合下，存在效用值为负的情况。例如，超市临期处理商品时，往往降价促销，存在亏本的情况。超市决策者可以通过指定捆绑销售措施来稍微挽回损失，故需要提出能同时处理正负效用的HUPM方法。有研究者提出含有负效用的高效用模式挖掘方法。本节根据模式划分方法进行分类总结，包括基于全集、精简和融合的模式。

3.1全集模式

全集模式是指传统意义上的高效用模式挖掘结果，即找到所有满足效用值大于等于最小效用阈值的所有项集。Chu等人首次提出基于两阶段的含有负效用的模式挖掘算法HUINIV-Mine[12]，算法利用重定义事务加权效用上界高估含有负效用的项集效用，保证项集中最少含有一个外部效用为正的项，并通过再次数据库扫描验证，故存在一定时空局限性。

3.1.1基于模式增长的方法

为解决基于候选生成-测试方法的局限性且避免生成数据集中实际不存在的候选项集提出了基于模式增长的方法。UP-GNIV[11]算法仅需两次数据库扫描，引入两种过滤策略删除负项效用（Removing Negative item Utilities， RNU）和剪枝负项集（Pruning Negative Itemsets， PNI）以去除含有负效用的项来提高挖掘效率。实验结果表明，该算法在执行时间和扩展性方面优于算法HUINIV-Mine[12]。EHIN[29]算法为减少内存消耗，采用事务库投影和事务合并技术，另外引入效用数组来计算重定义的本地效用（Redefined Local Utility， RLU）和重定义的子树效用（Redefined Subtree Utility， RSU）的新上界。基于此，运用RLU-Prune和RSU-Prune策略剪枝搜索空间。为挖掘出数量较少且更有意义的模式。EHNL[58]算法引入長度约束的概念，利用最小长度约束删除大量短项目集，最大长度约束来限制过长的项集，从而使得生成的关联规则更具代表性，此外，结合事务合并技术降低算法计算成本。

在动态数据库上，Li等人提出了两种基于滑动窗口的挖掘含有负效用的高效用项集算法，即MHUI-BIT-NIP[59]和MHUI-TID-NIP[59]，两者分别采用了BITvector和TIDlist的项目表示法以加快当前滑动窗口内项集的挖掘速度，同时，开发LexTree-2HTU结构维护窗口内2-项集的高事务加权效用。

3.1.2基于列表的方法

单阶段算法FHN[60]是FHM[2]算法的一种扩展，开发新的列表结构PNU-List应对负项的出现，且项的正负效用值采用单独的列表结构存储。此外，应用基于估计效用共现剪枝结构（Estimated Utility Co-occurrence Structure， EUCS）的剪枝策略和剩余效用剪枝策略。经实验证明，该算法在时空效率上均优于HUINIV-Mine[12]。随后，在FHN的扩展版本[28]中添加LA-Prune剪枝策略再次缩小搜索空间。GHUM[61]算法开发了一个简化效用列表结构，同时，基于项集效用反单调特性提出了A-Prune和N-Prune剪枝策略来降低列表连接成本。陈丽娟提出EHINM[62] 算法，该算法应用了改进的列表结构，包含三元组（tid，rutil，rpnu），其中rpnu为重新定义的剩余效用值。考虑到负效用在项集扩展时对事务效用的影响，引入RPNU和RTWU两种紧凑上界并提出三种剪枝策略。

面对不确定事务数据库，HUPNU[16]算法采用新的垂直列表结构PU±-list存储正负项并提出六种修剪策略提前修剪无希望的项。此外，张妮等人首次提出在数据流中挖掘含有负项的HUPM算法HND[15]。受ULB-Miner算法启发，开发出新的列表索引结构（List Index Structure， LIS）。不同于传统效用列表，此结构通过内存重用策略降低内存消耗成本，大大提升了挖掘性能。

3.2精简模式

因全集模式具有产生大量候选集导致项集冗余和最小效用阈值设置困难的问题，精简高效用模式应运而生，主要包括最大高效用模式、闭合高效用模式和Top-k高效用模式等。本小节将从这一角度总结含有负效用的模式挖掘方法。

Top-k模式不需要设置最小效用阈值，仅需用户提供生成具体高效用模式数量。Gan等人提出了一种挖掘具有正负效用的HUIs的通用算法TopHUI[13]，设计了PNU-List结构存储正负项信息，采用四种自动提升最小效用阈值方法，分别为基于项的实际效用提升最小阈值（Raising threshold based on real Item Utilities， RIU）策略、基于事务效用提升阈值（Raising threshold based on Transaction Utilities， RTU）策略、基于重定义的事务加权效用提高阈值（Raising threshold based on Redefined Transaction Weighted Utility， RRTWU）策略和基于候选项效用提高阈值（Raising the threshold by the Utilities of Candidates， RUC）策略，还引入数据库投影和事务合并技术减少数据库扫描成本，并应用基于数组的效用计数技术快速计算项集上界值，同时采用了RTWU-Prune、RU-Prune、LA-Prune和Leaf-Prune剪枝策略提高挖掘效率。Sun等人提出基于模式增长的THN[63]算法，该算法基于RLU和RSU提出两种剪枝策略并引入一种基于重定义事务加权效用上界的最小效用阈值提升策略找到模式的前K项，此外，结合数据库合并和投影技术降低数据库扫描成本。TKN[64]算法调整LIU结构存储正负效用，引入正项的实际效用（Positive Real Item Utility， PRIU）提升策略、基于LIU结构的正项（Positive LIU-Exact， LIU-E）提升策略以及基于LIU结构的正项下边界（Positive LIU-Lower Bound， LIU-LB）提升策略来快速提高最小效用阈值，泛化本地效用和子树效用关键剪枝属性并提出两种新的剪枝策略。

Singh等人提出CHN[65]算法挖掘含有负效用的闭合高效用项集，算法利用RSU-Prune缩小搜索空间并且利用双向扩展技术对搜索空间进行闭包检查。

3.3融合模式

為处理不同应用场合下的问题，含有负效用的模式与其他模式融合。On-shelf高效用模式除了考虑商品数量和利润外，同时引入了商品的上架时间周期。TS-HOUN[66]算法首次结合负效用概念和上架时间，通过三次数据库扫描，从时间数据库中挖掘出含有负效用的货架HUIs。由于该算法是两阶段算法的扩展，故挖掘效率并不高。Fournier-Viger等人提出基于效用列表的FOSHU[67]算法，该算法避免了为每个时间段挖掘结果合并，同时挖掘所有时间段以减少模式连接开销。实验结果表明，该算法比TS-HOUN[66]算法快近3个数量级，内存占用也大幅度降低。针对货架上的Top-k HUIs挖掘问题，Dam等人提出基于效用列表和估计共现最大周期率结构（Estimated co-occurrence Maximum Period Rate Structure， EMPRS）的KOSHU[68]算法，引入实际1-项集的相关效用阈值提升策略（the Real 1-Itemset Relative Utilities threshold raising strategy， RIRU）和实际2-项集的相关效用阈值提升策略（The Real 2-itemset Relative Utilities Threshold raising strategy， RIRU2），并应用估计最大周期率剪枝（Estimated Maximum Period Rate Pruning， EMPRP）策略、2-项集的共现剪枝（Concurrence Existing of a pair 2-itemset Pruning， CE2P）策略和周期效用剪枝（Period Utility Pruning， PUP）策略减少列表连接次数。针对动态数据库，Radkar等人提出FUPT-HOUIN[69]算法，引入FUP概念构造效用树挖掘含负项的货架HUIs。

Xu等人提出挖掘含有负项值的高效用序列模式算法HUSP-NIV[70]。采用LQS-Tree存储高效用序列并通过I-级联和S-级联方法生成候选序列。MHAUIPNU[22]算法从具有正负效用数据库中挖掘HAUIs，提出更严格的tubpn上界模型和新的列表结构TUBPNU-List，基于上界和负效用相关属性设计三种剪枝策略。

3.4小结

本节从模式划分的角度分析并总结了含有负效用的HUPM方法，包含全集模式、精简模式和融合模式的算法。图2从模式划分角度总结分析了含有负效用的模式挖掘算法。

此外，本小结比较了各种划分类别中具有代表性的算法，并在数据集上分析了部分算法的时空效率。全集模式旨在挖掘出所有满足最小效用阈值的项集，本节将其分为基于模式增长的和基于列表的算法。基于模式增长的算法可降低数据库扫描成本，以UP-GNIV[11]算法为代表，在运行时间和扩展性方面均优于基于先验的HUINIV-Mine[12]算法，但递归构造条件模式树挖掘项集仍需花费大量时间；基于列表的算法引入了垂直的表结构加快了挖掘速度。例如，FHN[60]算法在时空效率均优于UP-GNIV算法，但其局限性在于仍需要大量内存维护列表信息。针对全集模式生成的候选项集数量大、项集冗余和最小效用阈值设置困难的问题，提出了精简模式。本节将其分为Top-k模式和闭合模式。TopHUI[13]算法首次在Top-k模式中考虑负项，解决了最小效用阈值设置困难的问题。闭合模式通过去除冗余项集克服了传统HUPM的局限性，CHN[65]算法首次在闭合模式中考虑负项，经实验，该算法在密集和大部分稀疏数据集上均优于FHN[60]算法，速度提升了约44.8倍且内存需求为FHN算法的7.4%。此外，含有负效用的模式还与其它模式结合，例如On-shelf高效用模式、序列高效用模式和高平均效用模式等。

以上算法在实际应用中，时空效率尤为重要，但其通常受数据集的影响。实验中常见的通用数据集大致分为密集和稀疏两类，密集数据集包含Mushroom、Accidents和Chess等，稀疏数据集包含Retail和Kosarak等。在密集数据集Chess上，FHN[60]算法的执行速度是HUINIV-Mine[12]算法的500倍，内存消耗为HUINIV-Mine算法的0.4%，其主要原因为在于HUINIV-Mine算法多次扫描数据库，而FHN算法仅需两次扫描数据库且应用更严格的上界，此外，该方法不产生候选项集，故无需花费大量内存维护候选项集；EHIN[29]算法在Chess数据集上的表现优于FHN算法，在minutil=120k时，算法速度比为25∶1，主要原因在于密集数据集中存在大量重复项集，该算法采用投影合并技术能有效缩减数据库规模，而FHN算法通过组合较小的项目集来探索项目集的搜索空间，故性能不佳。在稀疏数据集Retail上，FHN算法优于THN[63]算法和CHN[65]算法，由于零售数据集包含大量不同的项，事务合并需要花费大量时间来合并事务，故THN[63]和CHN[65]算法在高度稀疏的数据集上表现不佳，但内存消耗依然很少。

最后，以经典算法FHN为例，分析含有负效用的高效用模式挖掘算法的时间复杂度，它的时间复杂度主要体现在数据库扫描、1-项集列表构建、EUCS的构建以及递归搜索方面。设n为数据库中的事务总数，m为不同项的个数，w为平均事务长度。首次扫描数据库的时间复杂度为O（nw），此后进行单个项的排序，时间复杂度为O（mlog2m）。第二次扫描数据的过程中，同时构建所有1-项集效用列表和EUCS结构，设l为项的个数，时间复杂度分别为O（ln）和O（nl（l－1）/2）。挖掘项集的时间复杂度为O（2l－1－l），故总的时间复杂度为以上各个阶段的时间复杂度之和，即O（2l）。由于EUCS结构占用少量内存空间，空间复杂度为O（l2）。

4扩展高效用模式

随着研究不断深入，效用挖掘领域也产生了大量新兴高效用模式。本节主要介绍模糊高效用模式、相关高效用模式、占用高效用模式和跨层级高效用模式。

4.1模糊高效用模式

效用挖掘是指在事务数据库中找到HUIs，由于无法反映项目之间的数量关系和利润的模糊程度，引入定量数据库和模糊集理论。例如通过模式{牛奶：1， 面包：5}，用户难以理解商品售卖情况的好坏。通过引入模糊概念将数量关系对应于语言的模糊程度，分别将牛奶和面包的售卖情况视为“低”量水平和“中”量水平，这有利于营销者理解并制定销售计划。本节总结了模糊高效用模式，包括基于传统的和基于智能优化的算法。HUFI-Miner[17]算法将量化值转化为模糊区域并利用外部效用信息表计算模糊项集效用以找到模糊高效用项集（High Fuzzy Utility Itemsets， HFUIs）。同时，利用隶属函数对应语言域值和隶属度值评价项集的模糊效用。TPFU[71]算法引入模糊效用上界模型来维持模糊集的DC属性，同时引入模糊集的最小算子概念来评估项集的模糊效用，在两个阶段中寻找所有的HFUIs。FUIM[72]算法设计了一个模糊效用列表以实现快速挖掘，并利用實际模糊效用与剩余效用之和约束搜索空间。Hong等人提出基于树挖掘算法[73]，引入FP-Tree结构来维护候选项集信息。经过实验表明，该方法在时间和内存消耗上均优于TP-TFU。

上述方法通过改变数据结构或设计剪枝策提高挖掘性能，而面对大数据环境，仍存在局限性。研究者们结合智能优化算法提出了一些新颖的挖掘方法。Wu等人将进化计算引入该领域，首次提出了基于遗传算法框架的HUFI-GA[74]算法，该算法对模糊项编码来表示为遗传空间的染色体，通过选择、交叉和变异运算并引入蒸发策略以发现更多潜在的HFUIs。EA-HUFIM[75]算法引入大型数据库最大效用的模糊项目集（High Database-max utility Fuzzy Itemset， HDFI）概念和精英学习策略。在突变运算中，向理想的方向产生候选项并删除不必要的后代，此外，该算法还应用了模糊映射和事务映射避免多余运算。

4.2相关高效用模式

由于在HUPM中主要考虑项集的效用，而很少关注项目之间的相关性，故挖掘结果中存在大量无意义的模式。以购物篮数据为例，项集中某项具有较高的利润会使得项集整体是高利润的，但这种罕见购买现象的出现不足以推荐与其一起购买的商品，故此时的销售决策和推销建议往往是无效的。例如{电脑，面包}是一个HUI，由于电脑的价格较高，则与任何商品组合都可能成为HUI。此时向买电脑的客户推荐面包是不合适的，因为它们很少一起出售。为解决这类问题，结合项集效用和相关性，研究者们提出了相关高效用模式，其中既是HUIs且相关性度量值不小于最小效用阈值的项集被定义为相关高效用项集（Correlated High Utility Itemsets， CoHUIs）。常见的相关性度量有All-confidence[76]、Bond[77]和Kulc[78]等。本节依据相关高效用挖掘算法采用的关键技术，分为基于列表的和其他的技术。

在现有的相关高效用模式挖掘算法中，大多为基于效用列表的方法。Fournier-Viger等人提出FCHM[18]算法来挖掘CoHUIs，并衍生出FCHMall-confidence[79]和FCHMbond[79]两个算法版本，该算法集成了多种策略以有效地发现CoHUIs。实验证明，算法比FHM快两个数量级以上且舍弃掉大量弱相关的HUIs。Gan等人提出基于Kulc度量的CoUPM[80]算法，采用含有支持度计数的效用列表计算相关性。基于此结构，引入基于Kulc值的有序向下闭包属性的修剪策略（pruning strategy using the Sorted downward closure Property of Kulc value， SPK）和基于效用上界的剪枝策略（pruning strategy using the Upper Bound on Utility， UBU）。ULB-CHMiner[81]算法引入效用列表缓冲区结构，通过内存重用策略降低内存消耗。单阶段算法CoHAI-miner[21]结合平均效用度量，提出SAU-list结构存储项集信息并设计三种剪枝策略挖掘相关的HAUIs。此外，考虑项集数量对效用挖掘的影响，Nouioua等人提出CHUQI-Miner[82]算法挖掘相关的定量高效用项目集，构建基于Q-项集的事务加权效用共现结构（Transaction weighted utility of Q-items Co-occurrence based Structure， TQCS），同时，开发出用于修剪非相关Q-项集的其它策略，在一定程度上删减了弱相关的模式且保留了HUIs之间的数量关系。

除了上述方法外，还有基于投影、树等其它技术的方法。基于数据库投影技术，Gan等人提出CoHUIM[83]算法挖掘非冗余的CoHUIs，该算法依据Kulc的排序向下闭包特性和剩余效用剪枝。Saeed等人提出了一种基于效用树结构的ECoHUPM[84]算法以挖掘具有强相关性项的高效用模式，该算法提出两种剪枝策略，基于效用与路径效用之和的上界属性（Upper Bound property based on summation of Utility and the Path Utilities， UBUPU）剪枝策略和基于节点效用的下界属性（Lower Bound property based on the Node Utility， LBNU）剪枝策略减少搜索空间并提高挖掘性能。

4.3其他新兴高效用模式

占用率度量用于评估模式在事务中的占比状况，从而得到代表性模式。传统的HUPM未评估模式占用情况，例如，即使模式X出现在多个事务中，但是在单个事务中并未占用该事务大部分效用，故无法真正代表这些事务。此时进行模式推荐可能是误导性的。为解决上述问题，结合占用度量和效用度量，提出效用占用概念和高效用占用模式挖掘。

OCEAN[19]算法首次引入效用占用度量评估模式对事务总效用的贡献，主要使用每个事务中的模式相对效用比率来描述用户习惯。但模式挖掘不完整且效率不高。HUOPM[85]算法结合用户兴趣、模式频率和效用占用率提取模式，引入效用-占用列表（Utility-Occupancy List， UO-List）和频率-效用表（Frequency-Utility Table， FU-Table）两种紧凑结构，无需生成候选就能得到模式的实际效用占用，有效找到完整的占用高效用模式。

UHUOPM[86]算法考虑不确定的复杂数据，提出概率效用占用列表（Probability-Utility-Occupancy List， PUO-List）和概率频率效用表（Probability-Frequency-Utility Table， PFU-List）降低数据库扫描成本，首次在不确定数据库中挖掘占用高效用模式。

随着研究的不断深入，有研究者将分类法与高效用项集挖掘任务相结合。例如，药酒和参茸都属于营养保健品，巧克力和果冻等都属于糖果，且营养保健品和糖果均为食品的子类别。分类法的引入可以在语义上将项目泛化产生广义项集（如例子中的食品、营养保健品和糖果）。由于傳统的HUPM没有考虑项目的分类法，只能挖掘分类树中的最低层项集（药酒、参茸、巧克力和果冻），即使营养保健品和糖果这些项是HUI，也无法被发现，故提出了在多个项目级别上挖掘高效用项集的新任务，称为跨层级的高效用模式挖掘。

ML-HUI Miner[87]算法在多个抽象层级上挖掘，将提取高效用的不同粒度级别的项集定义为广义高效用项集（Generalized High Utility Itemset， GHUIs）。但此算法只能找到相同抽象级别上的HUIs，无法找到分布在不同级别上的有意义模式且未利用分类关系缩小搜索空间。为解决上述问题，Fournier-Viger等人定义了更一般的跨层级的HUPM问题，并提出名为CLH-Miner[20]的算法。该算法允许挖掘结果中混合不同层级的项。同时在连接扩展的基础上，引入项集分类扩展方式并提出分类效用列表结构保存项集X的效用信息以及指向分类法X的孩子结点指针。此外，采用剩余效用剪枝策略减少项集的分类扩展连接。TKC[88]算法无需设置固定的最小效用阈值，通过提升最小效用阈值输出前K个符合条件的模式。随后，Tung等人提出了FEACP[89]算法，该算法扩展了紧凑的上界，通过本地效用和子树效用来缩小搜索空间并将主要项集和次要项集的概念扩展到广义项集以挖掘跨层级的项集。

4.4小结

近年来，大量新颖的高效用模式类型涌现，针对现实生活中不同应用场景，学者们还提出了多种扩展高效用模式。为解决传统HUPM在定量数据集上挖掘无法用语言模糊程度表达数量关系的问题，故提出了模糊高效用模式，主要采用模糊隶属函数处理项集效用，将交易中每个项目的数量也被转换为更适合人类思维的语言区域，通过语言的模糊程度评价项集的模糊效用。相关高效用模式解决了传统HUPM结果集中项之间弱相关的问题，通过采用不同的相关度量，有效删减弱相关的项集并降低销售决策中的误导性风险。占用高效用模式结合效用度量和占用度量，删减模式占用率较低的事务，因此有效评估了模式的占用情况并从中提取更加有意义的模式。此外，结合分类法信息，在多个抽象级别上挖掘HUIs，提出跨层级的高效用模式。

5结束语

本文对现有衍生高效用模式挖掘算法进行了系统综述，概述了衍生高效用模式所解决的问题和发展现状，归纳了各类衍生高效用模式并通过图表详细地给出算法的数据结构、剪枝算法、对比算法以及优缺点等。由于数据的多态性和需求的复杂性，衍生高效用模式在不断发展和完善以适应现阶段的需求，未来该领域仍存在诸多研究机会。

1） 基于智能优化算法的衍生高效用模式

随着项的多样性和数据集大小不断增加，在先前的工作中存在“组合爆炸问题”，因此发现所需信息的搜索空间是巨大的，故先前方法很难在具有大量记录和项目的数据库中应用。而面对庞大的数据量，智能优化算法能根据适应度函数在一定时间内快速找到最优解或近似最优解，为突破传统HUPM挖掘算法的性能瓶颈提供新的解决思路，现已在HUPM问题上初见成效，而对于更为复杂的应用场景和庞大的数据量，有必要在衍生模式中引入智能优化算法提高挖掘效率。在未来的工作中，考虑到智能优化算法快速挖掘的特性，可将其引入以挖掘高平均效用模式、含负效用的高效用模式等复杂的衍生模式。

2） 跨层级的模式挖掘

现阶段跨层级模式针对多种数据形态（如增量数据、数据流、序列等）和不同应用场景（如隐私保护等）的研究较少，该领域仍有很大发展潜力。此外，挖掘出的跨层级项集，虽然包含有用的分类信息，但面对较深的分类树，结果集中会出现过于模糊的项集，这同样不利于决策和推荐。在未来的工作中，应设计一种方法来约束跨层级数，从而减少冗余信息的挖掘，同时将分类法与其它模式结合用于处理更为复杂的问题，并在动态数据中搜索有趣的跨层级模式。

3） 并行分布式的高效用模式挖掘

目前大多数挖掘算法均集中于单个机器，处理大型数据集的能力有限，从而影响算法执行效率。而并行计算允许多个任务同时执行，多核并行计算架构能极大提升HUPM算法性能。随着商业数据集的快速增长，基于分布式的挖掘可以进一步扩大挖掘任务以适应大数据环境，因此有必要利用Hadoop或者Spark等分布式平台开发有效的挖掘算法来揭示决策所需的知识，使得算法能在大型数据集上实现更深层次的并行。

参考文献

[1] AGRAWAL R， IMIELIN＇SKI T， SWAMI A. Mining association rules between sets of items in large databases[C]//Proceedings of the 1993 ACM SIGMOD International Conference on Management of Data， Washington， USA， 1993： 207-216.

[2] FOURNIER-VIGER P， WU C W， ZIDA S， et al. FHM： faster high-utility itemset mining using estimated utility co-occurrence pruning[C]//Proceedings of the International Symposium on Methodologies for Intelligent Systems， Roskilde， Denmark， 2014： 83-92.

[3] HONG T P， LEE C H， WANG S L. Effective utility mining with the measure of average utility[J]. Expert Systems with Applications， 2011， 38（7）： 8259-8265.

[4] HONG T P， LEE C H， WANG S L. Mining high average-utility itemsets[C]//Proceedings of the 2009 IEEE International Conference on Systems， Man and Cybernetics， San Antonio， USA， 2009： 2526-2530.

[5] LIU Y， LIAO W K， CHOUDHARY A. A two-phase algorithm for fast discovery of high utility itemsets[C]//Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining， Hanoi， Vietnam， 2005： 689-695.

[6] LAN G C， HONG T P， TSENG V S. A projection-based approach for discovering high average-utility itemsets[J]. Journal of Information Science and Engineering， 2012， 28（1）： 193-209.

[7] LIN C W， HONG T P， LU W H. Efficiently mining high average utility itemsets with a tree structure[C]//Proceedings of the Asian Conference on Intelligent Information and Database Systems， Hue City， Vietnam， 2010： 131-139.

[8] LIN J C W， LI T， FOURNIER-VIGER P， et al. An efficient algorithm to mine high average-utility itemsets[J]. Advanced Engineering Informatics， 2016， 30（2）： 233-243.

[9] YUN U， KIM D. Mining of high average-utility itemsets using novel list structure and pruning strategy[J]. Future Generation Computer Systems， 2017， 68： 346-360.

[10] 王敬華， 罗相洲， 吴倩. 基于效用表的快速高平均效用挖掘算法[J]. 计算机应用， 2016， 36（11）： 3062-3066.

WANG J H， LUO X Z，WU Q. Fast high average-utility itemset mining algorithm based on utility-list structure[J]. Journal of Computer Applications， 2016， 36（11）： 3062-3066.

[11] SUBRAMANIAN K， KANDHASAMY P. UP-GNIV： an expeditious high utility pattern mining algorithm for itemsets with negative utility values[J]. International Journal of Information Technology and Management， 2015， 14（1）： 26-42.

[12] CHU C J， TSENG V S， LIANG T. An efficient algorithm for mining high utility itemsets with negative item values in large databases[J]. Applied Mathematics and Computation， 2009， 215（2）： 767-778.

[13] GAN W， WAN S， CHEN J， et al. TopHUI： top-k high-utility itemset mining with negative utility[C]//Proceedings of the 2020 IEEE International Conference on Big Data， Atlanta， USA，2020： 5350-5359.

[14] HONG T P， LEE C H， WANG S L. An incremental mining algorithm for high average-utility itemsets[C]//Proceedings of the 2009 10th International Symposium on Pervasive Systems， Algorithms， and Networks， Kaohsiung， China， 2009： 421-425.

[15] 張妮， 韩萌， 王乐， 等. 基于滑动窗口的含负项高效用模式挖掘方法[J]. 郑州大学学报（理学版）， 2022， 54（4）： 55-63.

ZHANG N， HAN M， WANG L，et al. Mining high utility patterns with negative utility over data stream[J]. Journal of Zhengzhou University（Natural Science Edition）， 2022， 54（4）： 55-63.

[16] GAN W， LIN J C W， FOURNIER-VIGER P， et al. Mining high-utility itemsets with both positive and negative unit profits from uncertain databases[C]//Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining， Jeju， Korea， 2017： 434-446.

[17] WANG C M， CHEN S H， HUANG Y F. A fuzzy approach for mining high utility quantitative itemsets[C]//Proceedings of the 2009 IEEE International Conference on Fuzzy Systems， Jeju， Korea，2009： 1909-1913.

[18] FOURNIER-VIGER P， LIN J C W， DINH T， et al. Mining correlated high-utility itemsets using the bond measure[C]//Proceedings of the International Conference on Hybrid Artificial Intelligence Systems， Seville， Spain， 2016： 53-65.

[19] SHEN B， WEN Z， ZHAO Y， et al. Ocean： fast discovery of high utility occupancy itemsets[C]//Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining， Auckland， New Zealand， 2016： 354-365.

[20] FOURNIER-VIGER P， WANG Y， LIN J C W， et al. Mining cross-level high utility itemsets[C]//Proceedings of the International Conference on Industrial， Engineering and Other Applications of Applied Intelligent Systems， Kitakyushu， Japan， 2020： 858-871.

[21] SETHI K K， RAMESH D. Correlated high average-utility itemset mining[C]//Proceedings of the International Conference on  Evolution in Computational Intelligence，Surathkal， India， 2021： 485-497.

[22] YILDIRIM I， CELIK M. Mining high-average utility itemsets with positive and negative external utilities[J]. New Generation Computing， 2020， 38（1）： 153-186.

[23] SINGH K， SINGH S S， KUMAR A， et al. High utility itemsets mining with negative utility value：a survey[J]. Journal of Intelligent & Fuzzy Systems， 2018， 35（6）： 6551-6562.

[24] SINGH K， KUMAR R， BISWAS B. High average-utility itemsets mining： a survey[J]. Applied Intelligence， 2022， 52（4）： 3901-3938.

[25] 张妮， 韩萌， 王乐， 等. 基于正负效用划分的高效用模式挖掘方法综述[J]. 计算机应用， 2022， 42（4）： 999-1010.

ZHANG N， HAN M， WANG L， et al. Survey of high utility pattern mining methods based on positive and negative utility division[J]. Journal of Computer Applications， 2022， 42（4）： 999-1010.

[26] ALMOQBILY R S， RAUF A， QURADAA F H. A survey of correlated high utility pattern mining[J]. IEEE Access， 2021， 9： 42786-42800.

[27] 李慕航， 韩萌， 陈志强， 等. 面向复杂高效用模式的挖掘算法综述[J]. 广西师范大学学报（自然科学版）， 2022， 40（3）： 13-30.

LI M H， HAN M， CHEN Z Q， et al. Survey of algorithms oriented to complex high utility pattern mining[J]. Journal of Guangxi Normal University （Natural Science Edition）， 2022， 40（3）： 13-30.

[28] LIN J C W， FOURNIER-VIGER P， GAN W. FHN： an efficient algorithm for mining high-utility itemsets with negative unit profits[J]. Knowledge-Based Systems， 2016， 111： 283-298.

[29] SINGH K， SHAKYA H K， SINGH A， et al. Mining of high-utility itemsets with negative utility[J]. Expert Systems， 2018， 35（6）： e12296.

[30] AGRAWAL R， SRIKANT R. Fast algorithms for mining association rules in large databases[C]//Proceedings of the 20th International Conference on Very Large Data Bases， Santiago de Chile， Chile， 1994： 487-499.

[31] LIN J C W， LI T， FOURNIER-VIGER P， et al. Efficient mining of high average-utility itemsets with multiple minimum thresholds[C]//Proceedings of the Industrial Conference on Data Mining， New York， USA， 2016： 14-28.

[32] WU J M T， TENG Q， LIN J C W， et al. Updating high average-utility itemsets with pre-large concept[J]. Journal of Intelligent & Fuzzy Systems， 2020， 38（5）： 5831-5840.

[33] 任家東， 王倩， 王蒙. 一种基于频繁模式有向无环图的数据流频繁模式挖掘算法[J]. 燕山大学学报， 2011， 35（2）： 115-120.

REN J D， WANG Q， WANG M. An algorithm based on frequent patterns directed acyclic graph for mining frequent patterns from data stream[J]. Journal of Yanshan University， 2011， 35（2）： 115-120.

[34] 姜玫. 平均高效用项集挖掘算法研究[D]. 大连： 大连理工大学， 2013.

JIANG M. Research on average high utility itemsets mining algorithm[D]. Dalian： Dalian University of Technology， 2013.

[35] LU T， VO B， NGUYEN H T， et al. A new method for mining high average utility itemsets[C]//Proceedings of the IFIP International Conference on Computer Information Systems and Industrial Management， Ho Chi Minh City， Vietnam， 2015： 33-42.

[36] KIM D， YUN U. Efficient algorithm for mining high average-utility itemsets in incremental transaction databases[J]. Applied Intelligence， 2017， 47（1）： 114-131.

[37] LIN J C W， REN S， FOURNIER-VIGER P， et al. Efficiently updating the discovered high average-utility itemsets with transaction insertion[J]. Engineering Applications of Artificial Intelligence， 2018， 72： 136-149.

[38] YUN U， KIM D， RYANG H， et al. Mining recent high average utility patterns based on sliding window from stream data[J]. Journal of Intelligent & Fuzzy Systems， 2016， 30（6）： 3605-3617.

[39] YUN U， KIM D， YOON E， et al. Damped window based high average utility pattern mining over data streams[J]. Knowledge-Based Systems， 2018， 144： 188-205.

[40] WU Y， LEI R， LI Y， et al. HAOP-Miner： self-adaptive high-average utility one-off sequential pattern mining[J]. Expert Systems with Applications， 2021， 184： 115449.

[41] WU Y， GENG M， LI Y， et al. HANP-Miner： high average utility nonoverlapping sequential pattern mining[J]. Knowledge-Based Systems， 2021， 229： 107361.

[42] LIN J C W， REN S， FOURNIER-VIGER P， et al. A fast algorithm for mining high average-utility itemsets[J]. Applied Intelligence， 2017， 47（2）： 331-346.

[43] LIN J C W， REN S， FOURNIER-VIGER P， et al. EHAUPM： efficient high average-utility pattern mining with tighter upper bounds[J]. IEEE Access， 2017， 5： 12927-12940.

[44] WU J M T， LIN J C W， PIROUZ M， et al. TUB-HAUPM： tighter upper bound for mining high average-utility patterns[J]. IEEE Access， 2018， 6： 18655-18669.

[45] KIM H， YUN U， BAEK Y， et al. Efficient list based mining of high average utility patterns with maximum average pruning strategies[J]. Information Sciences， 2021， 543： 85-105.

[46] LIN J C W， REN S， FOURNIER-VIGER P. MEMU： more efficient algorithm to mine high average-utility patterns with multiple minimum average-utility thresholds[J]. IEEE Access， 2018， 6： 7593-7609.

[47] SETHI K K， RAMESH D. High average-utility itemset mining with multiple minimum utility threshold： a generalized approach[J]. Engineering Applications of Artificial Intelligence， 2020， 96： 103933.

[48] WU T Y， LIN J C W， SHAO Y， et al. Updating the discovered high average-utility patterns with transaction insertion[C]//Proceedings of the International Conference on Genetic and Evolutionary Computing， Kaohsiung， China， 2017： 66-73.

[49] ZHANG B， LIN J C W， SHAO Y， et al. Maintenance of discovered high average-utility itemsets in dynamic databases[J]. Applied Sciences， 2018， 8（5）： 769.

[50] LIN J C W， SHAO Y， FOURNIER-VIGER P， et al. Maintenance algorithm for high average-utility itemsets with transaction deletion[J]. Applied Intelligence， 2018， 48（10）： 3691-3706.

[51] LAN G C， HONG T P， TSENG V S. Efficiently mining high average-utility itemsets with an improved upper-bound strategy[J]. International Journal of Information Technology & Decision Making， 2012， 11（5）： 1009-1030.

[52] YILDIRIM I， CELIK M. FIMHAUI： fast incremental mining of high average-utility itemsets[C]//Proceedings of the 2018 International Conference on Artificial Intelligence and Data Processing， Malatya， Turkey， 2018： 1-9.

[53] THILAGU M， NADARAJAN R. Efficiently mining of effective web traversal patterns with average utility[J]. Procedia Technology， 2012， 6： 444-451.

[54] 李霆. 基于不確定数据的高平均效用序列模式挖掘算法的研究[D]. 深圳： 哈尔滨工业大学， 2016.

LI T. Ming high average utility sequential patterns from uncertain databases[D]. Shenzhen： Herbin Institute of Technology， 2016.

[55] TRUONG T， DUONG H， LE B， et al. Efficient vertical mining of high average-utility itemsets based on novel upper-bounds[J]. IEEE Transactions on Knowledge and Data Engineering， 2018， 31（2）： 301-314.

[56] TRUONG T， DUONG H， LE B， et al. Efficient high average-utility itemset mining using novel vertical weak upper-bounds[J]. Knowledge-Based Systems， 2019， 183： 104847.

[57] PHUONG N， DUY N D. Constructing a new algorithm for high average utility itemsets mining[C]//Proceedings of the 2017 International Conference on System Science and Engineering， Ho Chi Minh City， Vietnam， 2017： 273-278.

[58] SINGH K， KUMAR A， SINGH S S， et al. EHNL： an efficient algorithm for mining high utility itemsets with negative utility value and length constraints[J]. Information Sciences， 2019， 484： 44-70.

[59] LI H F， HUANG H Y， LEE S Y. Fast and memory efficient mining of high-utility itemsets from data streams： with and without negative item profits[J]. Knowledge and Information Systems， 2011， 28（3）： 495-522.

[60] FOURNIER-VIGER P. FHN： efficient mining of high-utility itemsets with negative unit profits[C]//Proceedings of the International Conference on Advanced Data Mining and Applications， Guilin， China， 2014： 16-29.

[61] KRISHNAMOORTHY S. Efficiently mining high utility itemsets with negative unit profits[J]. Knowledge-Based Systems， 2018， 145： 1-14.

[62] 陈丽娟. 含有负项值的高效用项集挖掘算法研究[D]. 福州： 福州大学， 2018.

CHEN L J. Research on algorithm for mining high utility itemset with negative item values[D]. Fuzhou： Fuzhou University， 2018.

[63] SUN R， HAN M， ZHANG C， et al. Mining of top-k high utility itemsets with negative utility[J]. Journal of Intelligent & Fuzzy Systems， 2021， 40（3）： 5637-5652.

[64] ASHRAF M， ABDELKADER T， RADY S， et al. TKN： an efficient approach for discovering top-k high utility itemsets with positive or negative profits[J]. Information Sciences， 2022， 587： 654-678.

[65] SINGH K， SINGH S S， KUMAR A， et al. CHN： an efficient algorithm for mining closed high utility itemsets with negative utility[J]. IEEE Transactions on Knowledge and Data Engineering， 2018， 1（1）： 99-113.

[66] LAN G C， HONG T P， HUANG J P， et al. On-shelf utility mining-with negative item values[J]. Expert Systems with Applications， 2014， 41（7）： 3450-3459.

[67] FOURNIER-VIGER P， ZIDA S. FOSHU： faster on-shelf high utility itemset mining--with or without negative unit profit[C]//Proceedings of the the 30th Annual ACM Symposium on Applied Computing， Salamanca， Spain， 2015： 857-864.

[68] DAM T L， LI K， FOURNIER-VIGER P， et al. An efficient algorithm for mining top-k on-shelf high utility itemsets[J]. Knowledge and Information Systems， 2017， 52（3）： 621-655.

[69] RADKAR A N， PAWAR S. Mining high on-shelf utility itemsets with negative values from dynamic updated database[J]. International Journal of Advanced Studies in Computer Science and Engineering， 2015， 5（6）： 27-33.

[70] XU T， DONG X， XU J， et al. Mining high utility sequential patterns with negative item values[J]. International Journal of Pattern Recognition and Artificial Intelligence， 2017， 31（10）： 1750035.

[71] LAN G C， HONG T P， LIN Y H， et al. Fuzzy utility mining with upper-bound measure[J]. Applied Soft Computing， 2015， 30： 767-777.

[72] WAN S， GAN W， GUO X， et al. FUIM： fuzzy utility itemset mining [EB/OL].（2021-10-31）[2022-09-05].https：//arxiv.org/abs/2111.00307.

[73] HONG T P， LIN C Y， HUANG W M， et al. Mining temporal fuzzy utility itemsets by tree structure[C]//Proceedings of the 2019 IEEE International Conference on Big Data， Los Angeles， USA， 2019： 2659-2663.

[74] WU J M T， LIN J C W， FOURNIER-VIGER P， et al. A ga-based framework for mining high fuzzy utility itemsets[C]//Proceedings of the 2019 IEEE International Conference on Big Data， Los Angeles，USA， 2019： 2708-2715.

[75] YANG F， MU N， LIAO X， et al. EA-HUFIM： Optimization for fuzzy-based high-utility itemsets mining[J]. International Journal of Fuzzy Systems， 2021， 23（6）： 1652-1668.

[76] OMIECINSKI E R. Alternative interest measures for mining associations in databases[J]. IEEE Transactions on Knowledge and Data Engineering， 2003， 15（1）： 57-69.

[77] BOUASKER S， BEN YAHIA S. Key correlation mining by simultaneous monotone and anti-monotone constraints checking[C]//Proceedings of the Proceedings of the 30th Annual ACM Symposium on Applied Computing， Salamanca， Spain，2015： 851-856.

[78] WU T， CHEN Y， HAN J. Re-examination of interestingness measures in pattern mining： a unified framework[J]. Data Mining and Knowledge Discovery， 2010， 21（3）： 371-397.

[79] FOURNIER-VIGER P， ZHANG Y， LIN J C W， et al. Mining correlated high-utility itemsets using various measures[J]. Logic Journal of the IGPL， 2020， 28（1）： 19-32.

[80] GAN W， CHUN WEI J， CHAO H C， et al. CoUPM： Correlated utility-based pattern mining[C]//Proceedings of the 2018 IEEE International Conference on Big Data， Seattle， USA， 2018： 2607-2616.

[81] WU L， XIE G. Mining correlated high utility itemsets from MOOC data[C]//Proceedings of the 2021 6th International Conference on Big Data and Computing，Shenzhen， China， 2021： 49-54.

[82] NOUIOUA M， FOURNIER-VIGER P， QU J F， et al. CHUQI-Miner： mining correlated quantitative high utility itemsets[C]//Proceedings of the 2021 International Conference on Data Mining Workshops， Auckland， New Zealand， 2021： 599-606.

[83] GAN W， LIN J C W， FOURNIER-VIGER P， et al. Extracting non-redundant correlated purchase behaviors by utility measure[J]. Knowledge-Based Systems， 2018， 143： 30-41.

[84] SAEED R， RAUF A， QURADAA F H， et al. Efficient utility tree-based algorithm to mine high utility patterns having strong correlation[J]. Complexity， 2021， 2021： 7310137.

[85] GAN W， LIN J C W， FOURNIER-VIGER P， et al. HUOPM： high-utility occupancy pattern mining[J]. IEEE Transactions on Cybernetics， 2019， 50（3）： 1195-1208.

[86] CHEN C M， CHEN L， GAN W， et al. UHUOPM： High utility occupancy pattern mining in uncertain data[C]//Proceedings of the 2020 IEEE International Conference on Systems， Man， and Cybernetics， Toronto， Canada， 2020： 3066-3071.

[87] CAGLIERO L， CHIUSANO S， GARZA P， et al. Discovering high-utility itemsets at multiple abstraction levels[C]//Proceedings of the European Conference on Advances in Databases and Information Systems， Nicosia， Cyprus， 2017： 224-234.

[88] NOUIOUA M， WANG Y， FOURNIER-VIGER P， et al. Tkc： Mining top-k cross-level high utility itemsets[C]//Proceedings of the 2020 International Conference on Data Mining Workshops， Sorrento， Italy， 2020： 673-682.

[89] TUNG N， NGUYEN L T， NGUYEN T D， et al. Efficient mining of cross-level high-utility itemsets in taxonomy quantitative databases[J]. Information Sciences， 2022， 587： 41-62.

Survey of derived high utility pattern mining algorithms

Abstract： In the field of data mining， the task of high utility pattern mining has a high theoretical research value and a wide range of practical application scenarios. A series of derived high utility patterns are proposed for variable applications. Firstly， the high average utility pattern mining algorithms are discussed from the perspective of key technologies， mainly including Apriori-based， tree-based， list-based， projection-based and data structure-based algorithms. Secondly， high utility pattern mining algorithms containing negative utility based on complete set， concise set and integrated pattern are analytically discussed. Then， the extended high utility pattern algorithms are outlined and summarized from three aspects， including fuzzy high utility patterns， correlated high utility patterns and other emerging high utility patterns. Finally， in view of the shortcomings of the current research direction， the next research directions are given.

Keywords： derived high utility pattern; high average utility pattern; negative utility; fuzzy high utility pattern; correlated high utility pattern; survey