属性偏序形式结构的数学形式化

任蕴丽 宋佳霖 郑存芳 洪文学

摘要：属性偏序形式结构，作为一种基于人类认知原理和粒计算思想的知识发现和知识表示新理论，目前已有广泛的应用，但其理论基础缺乏抽象化数学化，这势必影响该理论的系统发展。针对上述问题，研究了属性偏序形式结构的数学形式化描述问题。首先，基于粒计算的思想提出了知识表示的形式化框架。在此基础上，通过定义对象集合的覆盖和最简覆盖，给出属性偏序形式结构的粒和粒群的概念，进而通过对粒衍生出粒群的充要条件的讨论，给出了属性偏序形式结构中的知识结构，从而完成属性偏序形式结构的数学形式化描述。最后，通过具体实例展示了利用数学形式化描述构造属性偏序形式结构的过程，并揭示了该过程所体现的人类认知规律。

关键词：形式背景；数学形式化；属性偏序形式结构；粒计算；概念认知学习

中图分类号： TP391.4  文献标识码： ADOI：10.3969/j.issn.1007-791X.2024.02.004

0引言

知识表示是认知科学领域的基础问题[1]。从认知计算的角度看，知识表示的基本认知单元是概念[2]。概念在学习、推理等几乎所有认知过程中都有一定意义[3]。形式概念分析创始人德国数学家Wille[4]于1982年首先提出了概念的数学定义，即形式概念是由内涵和外延所组成的二元有序组。在形式概念分析理论中，一个形式背景的所有概念依据其泛化和例化关系，构成一个完备格结构，即概念格，它是形式概念分析理论的核心知识结构。概念格的Hasse图是其所构成的知识结构的可视化表达。目前形式概念分析理论广泛应用于数据属性约简[5-7]、规则提取[8]、知识挖掘[9-10]等领域。然而，由于概念格的Hasse图是有交叉的网状图，所以当数据量较大时，其所表达的知识结构可视化效果不理想。同时，在形式概念分析理论中，内涵和外延通过属性幂集和对象幂集间的一对闭包算子来相互唯一确定，这就将人们认知事物的过程看作是一次完成的，然而在现实生活中，人们对客观事物的认知往往是一个渐进的过程，一开始人们的认知是模糊的片面的，但随着学习到事物更多的特征，人们对其认识才逐渐清晰和完善。因此，为了更好地反映人类认知的实际过程，迫切需要一种符合人类认知原理的知识发现和知识表示的方法。

属性偏序形式结构是洪文学教授[11-12]在形式概念分析的基础上，根据人类认知原理和粒计算思想提出来的知识发现和知识表示的可视化新理论。在事物所具有的多种属性（特征）中，有些属性可以覆盖较多的对象（事物），称其为共有属性，而有些属性则仅为个别对象所具有，称这样的属性是独有属性。在认知过程中，人们往往将具有共有属性的事物聚在一起，而将具有独有属性的对象彼此远离，从而达到区分事物的目的。在属性偏序形式结构中，以属性覆盖对象的多少来刻画属性的普遍性的强弱，普遍性强的属性置于结构的上层，特异性强的属性置于下层，从上往下属性的普遍性逐层递减，特异性逐层增强，从而达到认识和区分事物的目的，从下往上，属性的普遍性逐层增强，达到聚类的目的。属性偏序形式结构中的粒（节点）并不要求是形式概念，而是由属性决定的属性对象有序多元组。随着该结构中层次的加深，粒中的属性集和对象集逐渐实现相互唯一确定，从而很好地刻画人类对事物（对象）的认知过程。该结构的可视化表达即属性偏序形式结构图，是一个无交叉的图，可以将形式背景中蕴含的知识清晰地呈现出来。鉴于属性偏序形式结构理论符合人类认知原理，并且具有良好的可视化效果，该理论在概念认知学习领域吸引了学者们的关注，并且广泛地应用于中医药知识发现[13-17]、语义排歧[18-19]、医学诊断数据挖掘[20-21]等领域。

在属性偏序形式结构的应用研究发展迅速的同时，偏序形式结构的理论研究卻相对薄弱。文献[22-24]主要是从计算机算法优化和可视化等角度对属性偏序形式结构进行研究。文献[25]基于粒计算和三支决策的思想，探讨了三支属性偏序形式结构的构造方法。而有关属性偏序形式结构理论的基础研究，特别是该理论的数学形式化则很少有相关的研究成果。数学形式化框架可以为属性偏序形式结构的很多基本问题的系统研究提供坚实的基础，比如基于属性偏序形式结构的知识发现算法与解释、相关理论与概念认知学习的结合与进一步发展等。因此对该理论基本原理和方法的抽象的数学形式化描述是非常有价值的科学问题。

本文旨在探索属性偏序形式结构基本理论的数学形式化描述。首先，基于粒计算思想给出知识表示的形式化框架。在此基础上，通过定义对象集合的覆盖、最简覆盖，属性偏序形式结构中的粒、粒群等，讨论粒群构成的知识结构、簇集等，进而完成属性偏序形式结构（图）的数学形式化描述。

1基于粒计算思想的知识表示形式化框架

粒计算[26]的思想与人们在解决问题或认识客观事物时将部分事物不加区分地看作一个整体的处理方式是一致的。客观世界中的事物纷繁复杂，人们认识客观世界时，由于信息不完备、认知能力有限、所要解决的问题精度要求不高等原因，人们会很自然地将客观事物分成若干组、群或簇集，也就是说按照一定的准则将相似的或者相关的事物看作一个整体而不加区分，这些整体称为“粒”，这个过程可称为粒化。人们一般对粒内的事物不加区分，而关注不同粒间的关系。粒化时的标准不同，人们会得到精度不同的粒。粒的精度的大小可以称为粒度，粗粒度的粒涵盖较多的对象，粒化时所使用的标准较粗，反之，细粒度的粒则涵盖较少的对象，粒化的标准也更精细。每一次粒化所形成的粒都处在同一个粒层，同一个粒层中的粒构成对论域的一个覆盖或划分。人们对论域施以不同的粒化，会得到不同的粒层，将这些粒层按粒度从粗到细排列，可以得到多层次的知识体系。人们在认识客观世界或解决问题时，可以很自由地在不同的粒层间进行切换。

根据粒计算的思想，知识体系的表示形式可以是知识粒构成的分层次的结构。知识表示的形式化框架是三元组（D，G，R），其中D是数据，它包含了研究对象及其所具有的属性与特征，例如形式概念分析中的形式背景、粗糙集理论中的信息表等；G是根据某些标准由D中的对象生成的粒的集合；R是粒间的关系或在此基础上所生成的粒结构。

譬如，在形式概念分析中，数据D是由对象集、属性集及二者之间的二元关系组成的三元组，它能够反映每一个对象所具有的属性；形式概念分析中G里的粒是形式概念，即由外延和内涵组成的有序二元组，二者由对象幂集和属性幂集间的两个闭包算子相互唯一确定；形式概念分析中R是所有形式概念的集合上的偏序关系，它通过形式概念的外延（或内涵）的包含关系来定义，在此偏序关系基础上，全体粒（形式概念）构成了多层次的网状结构。这一结构就是形式背景（数据）中所蕴含的知识的表示，并且Hasse图可以将这一知识结构以图形的方式可视化表达。

此外，决策树、商空间等都符合上述知识表示的形式化框架。

2属性偏序形式结构的数学形式化描述

2.1属性偏序形式结构的基本思想

人类在认知客观世界时，往往会根据事物所具有的属性或特征，将相似或相近的事物聚集在一起，而使差异较大的事物远离相近的事物。同时，人类对客观事物的认知往往不是一次完成的，开始的认知比较模糊，随着获取事物越来越多的属性和特征，人们对它的认识才逐渐清晰。

为了反映人类认知的这一特征，将粒定义为属性（或属性集合）及其所描述的对象集合所组成的有序二元组。粒中的属性（或属性集合）的普遍性强弱有较大差别，有些属性（或属性集合）为较多对象所具有，从而有较强的普遍性，此时粒的粒度较大（粗）；而有些属性则仅有较少的对象才具有，所以它的普遍性较弱而特异性较强，此时粒的粒度较小（细）。在构造知识体系时，人们会自上而下地通过对普遍性强的属性（或属性集合）加入新属性而区分不同的事物，另一方面，人们还可以自下而上地通过去除特异性强的属性而将相似的事物聚类。因此，人类的知识体系的组织结构，一定是多层次的，在这一结构中，普遍性强的粗粒度的粒在上层，随着更多属性的加入，层次逐渐加深，粒的普遍性逐渐降低特异性逐渐加强，粒的粒度也逐渐加细，不同粒度的粒之间依据偏序关系相连接。

2.2属性偏序形式结构中的数据——形式背景及相关基础知识与形式概念分析类似，属性偏序形式结构所处理的数据也是以形式背景的形式呈现。为此，本小节先介绍形式概念分析中形式背景、形式概念等相关基础知识，并在此基础上，给出属性（属性集）的覆盖基数的概念及性质。

定义 1[4]形式背景K=（U，A，I）是由对象集U、属性集A及二者间的二元关系I所组成的三元组。对于x∈U，a∈A，表达式（x，a）∈I或xIa表示对象x具有属性a。

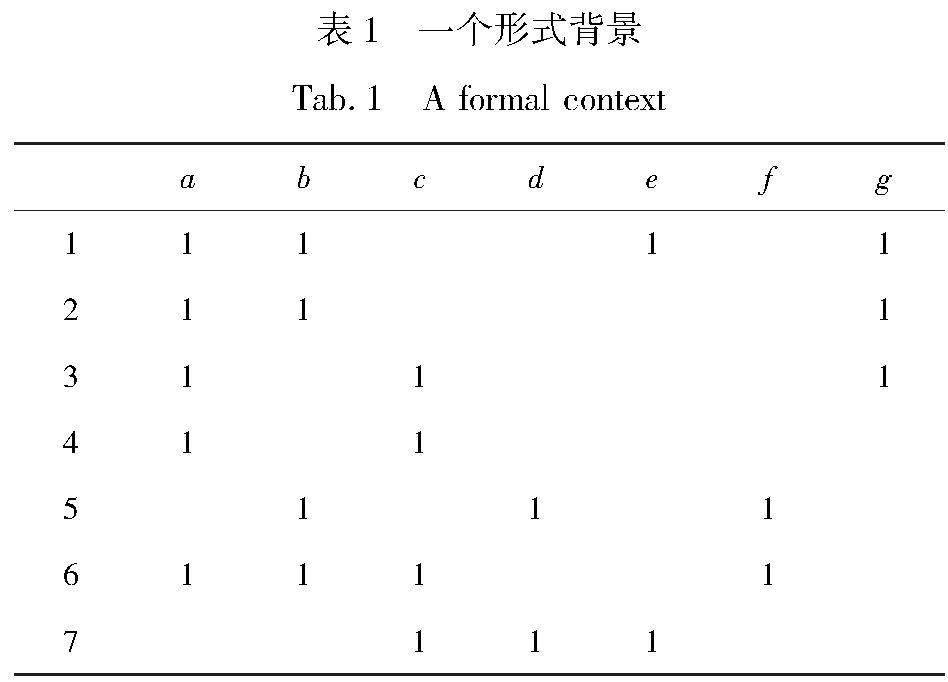
通常，形式背景可由形如表1的二值表格来表示。在表1中所示的形式背景中，U={1，2，3，4，5，6，7}，A={a，b，c，d，e，f，g}，第一行列出了所有的属性，第一列列出了所有的对象，在行列交叉点处的数字“1”表示相应行中的对象具有相应列中的属性，空白则表示相反的情形。

f（V）={a∈A|（u，a）∈I，u∈V}，

g（B）={u∈U|（u，b）∈I，b∈B}。

为了描述属性的普遍性强弱，给出属性的覆盖基数的概念。

性质1设K=（U，A，I）是一个形式背景，则有以下结论成立：

G（B∪C）≤min{G（B），G（C）}，

G（B∩C）≥max{G（B），G（C）}；

|g（B）∪g（C）|=G（B）+G（C）-G（B∪C）；

0，进而有|g（B）∪g（C）|=G（B）+G（C）；

G（B）+G（C）=|U|。

G（B∪C）≤min{G（B），G（C）}。

同理，G（B∩C）≥G（B）且G（B∩C）G（C），從而

G（B∩C）≥max{G（B），G（C）}。

3） |g（B）∪g（C）|=

|g（B）∪［g（C）-g（B）］|=

|g（B）|+|［g（C）-g（B）］|=

G（B）+|g（C）-g（B∪C）|=

G（B）+|g（C）|-|g（B∪C）|=

G（B）+G（C）-G（B∪C）。

4） 当B和C为互斥的属性集合时，G（B∪C）=|g（B∪C）|=|g（B）∩g（C）|=0。进一步由3）知|g（B）∪g（C）|=G（B）+G（C）。

5） 当B和C为对立的属性集合时，由4）可知G（B∪C）=0，代入3）中的公式可知G（B）+G（C）=|g（B）∪g（C）|=|U|。

由性质1的1）和2）可知，属性集的覆盖基数随着属性的增多而减小，随着属性的减少而增大，因此，属性集的覆盖基数可以作为衡量属性集普遍性强弱的一个度量。

为了方便表达，称g（B）是属性集B所覆盖的对象。

定义5在形式背景K=（U，A，I）中，如果属性a∈A满足G（a）=|U|，则称a为K中的一个最大共有属性。

性质2在形式背景K=（U，A，I）中，属性a是最大共有属性，当且仅当对任意的u∈U，有uIa，即g（a）=U。

2.3属性偏序形式结构中粒的数学形式化描述

对于任意BA，由于对象集合g（B）中的对象都具有B中的所有属性，所以它们可以聚成一个由属性集合B所决定的粒。但是为了表达形式背景中的知识结构，在属性偏序形式结构中，仅选取其中的一部分粒。为了描述粒选取的标准，给出对象集合的覆盖和最简覆盖的定义。

如果属性b1，b2，…，bk构成U1相对于A1的一个覆盖，可以说属性b1，b2，…，bk覆盖U1（相对于A1），或者{b1，b2，…，bk}是U1相对于A1的一个覆盖。

1） 属性b1，b2，…，bk构成U1相对于A1的一个覆盖；

2） 对于任意i∈{1，2，…，k}，{bj|1≤j≤k，j≠i}不构成U1相对于A1的一个覆盖；

对于U1相对于A1的最简覆盖b1，b2，…，bk，如果b1，b2，…，bk是U1相对于A1的完全覆盖，则称该覆盖是最简完全覆盖，否则为最简非完全覆盖。

下面给出属性偏序形式结构中粒的数学表达。

由于属性偏序形式结构中的粒涉及粒的选择问题，所以其中的粒以粒群的形式出现。

i=2，3，…，s，属性b1，b2，…，bs是O相对于Bc的最简覆盖。称bi是子粒Ni的核心属性，i=1，2，…，s。

在粒群（N;N1，N2，…，Ns）中，从对象的角度而言，子粒N1，N2，…，Ns构成顶点粒N的一个划分，如下图1所示。图1中虚线所示部分只有在最简非完全覆盖的情形才存在。从图中可以看到，粒群中顶点粒和子粒是通过子粒的核心属性建立联系的。

对于每一个子粒Ni（i=1，2，…，s），当Oi存在相对于Bic的最简覆盖时，还可以得到以Ni为顶点粒的新的粒群，依次下去可得到粒群构成的结构，如图2所示。图中虚线框住的每一部分都是一个粒群，从上往下，粒群对对象的描述逐渐加细。

2.4属性偏序形式结构中粒间关系及知识结构的数学形式化描述属性偏序形式结构中的粒通过最简覆盖构成一个双层的粒群，以粒群的子粒为顶点粒可以继续向下衍化出新的粒群……因此，目前组成属性偏序形式结构的关键问题有两个：1）确定首粒，这是整个结构构成的开端；2）确定粒群向下展开的终止条件。

关于首粒的确定，可以分成兩种情况：如果形式背景K存在最大共有属性a，则首粒为（a，U，U）；否则，首粒为（，U，U）。这里为表达上的简便，以a代替{a}，后续类似的简化不再赘述。

关于粒群向下展开的终止条件，有如下定理和推论。

充分性：如果存在u∈O，使得f（u）B，记

cs（s≤m）。进而可得以粒N=（B，g（B），O）为顶点粒的粒群（N;N1，N2，…，Ns），其中子粒为Ni=（Bi，g（Bi），Oi），i=1，2，…，s。这里，

不可展开成粒群的粒称为终点粒。

至此，可以得到属性偏序形式结构：从首粒出发，按照定理1充分性证明中的方法得到第一个粒群，其中的子粒是对论域U的一个粗糙的划分，进而再以子粒为顶点粒继续向下衍生出新的粒群，可得论域U的更细的划分。继续这个过程，直至子粒的对象仅具有该粒中的属性，此时的子粒即为终点粒，不会继续向下衍生新粒。

将粒群中的子粒置于顶点粒的下方，每个粒群中顶点粒与子粒间建立连接边，终点粒与底层粒（A，）间建立连接边，即得属性偏序形式结构图，记作APOSD（K）。在属性偏序形式结构图中，节点即为属性偏序形式结构中的粒，以后可以对两种说法不加区分。从横向看，属性偏序形式结构图中的每一层都是对论域U的一个划分，处在上层的划分粒度较粗，随着层次的加深，对论域U的划分逐层加细；从纵向看，每一条支路代表一个对象，每一个对象通过唯一的一条支路表达，支路上的各节点（粒）的核心属性即为该对象所具有的全部属性。属性偏序形式结构图是一个多层次的无交叉图，在形式背景中蕴含的知识结构的表示方面，具有良好的可视化效果。

定义9在形式背景K=（U，A，I）的属性偏序形式结构图中，以粒N=（B，g（B），O）为顶点粒的粒群及其向下衍生出的全部粒构成的结构称为簇集，记作Cluster（N）。

在簇集Cluster（N）中，对象的一个共同点是具有属性集B中的所有属性。当O=g（B）时，该簇集即为属性集B所覆盖（或者说描述）的全部对象所成的簇集，这是APOSD（K）的一个子图；当Og（B）时，该簇集是属性集B所覆盖的部分对象所组成的，为了得到属性集B所描述的全部对象所组成的簇集，只需取O=g（B），以N*=（B，g（B），g（B））为首粒，逐层向下衍生即可。

由于在属性偏序形式结构图中，除首粒之外，每一个粒N=（B，g（B），O）都是某个粒群的子粒，其中的O可通过式（1）计算得出。因此，粒N=（B，g（B），O）主要是由其属性集B决定的，所以有时可仅用粒三元组中的前两个元素作成的二元组来表示粒，即将图中的节点简记为N=（B，g（B））；进一步，属性集B是通过在顶点粒的属性集合上添加该粒的核心属性而得到的，因此，有时在属性偏序形式结构图中，仅以节点的核心属性标示节点。

3属性偏序形式结构数学形式化构造实例

表2所示的是著名的“生物和水”形式背景K=（U，A，I），其中对象1至8分别为水蛭、娃娃鱼、青蛙、狗、水草、芦苇、豆子和玉米。属性a至i分别表示需要水、水中生活、陆地上生活、需要叶绿素、双子叶植物、单子叶植物、能运动、有四肢和哺乳。

下面将按照第2章介绍的属性偏序形式结构的数学形式化描述，从首粒开始通过确定最简覆盖，构造粒和粒群，逐层向下衍生出该形式背景的整个属性偏序形式结构。

首先，由于属性a满足g（a）=U，所以首粒为N1=（a，U，U）。在子形式背景K1=（U，A-{a}，I|U×（A-{a}））下，G（b）=G（c）=5，G（d）=G（g）=4，G（f）=G（h）=3，G（e）=G（i）=1，取定覆盖基数最大的属性b。接下来，在子形式背景（U-g（b），A-{a，b}，I|（U-g（b））×（A-{a，b}））下覆盖基数最大的属性为属性c。由于g（b）∪g（c）=U，所以{b，c}是U相对于{a}c的一个覆盖。由于b和c都不能单独覆盖U，并且二者的覆盖基数在子背景K1下是最大的，所以{b，c}是U相对于{a}c的一个最简覆盖。因此可得首粒N1下的子粒为N1，1=（ab，g（ab），U∩g（b））=（ab，12356，12356），N1，2=（ac，g（ac），U∩g（c）-g（b））=（ab，34678，478）。这里为了简便，用12356来代替集合{1，2，3，5，6}，类似的简化不再赘述。三者构成的粒群为（N1;N1，1，N1，2），如图3所示。

此时，将形式背景中的生物分成N1，1所代表的水生生物和N1，2所代表的陆生生物两大类。

从而可得N1，1为顶点粒的粒群（N1，1;N1，1，1，N1，1，2），如图4所示。

此时，将水生生物分为N1，1，1所代表的水生动物和N1，1，2所代表的水生植物两类。

同样地，分别以N1，1，1和N1，1，2为顶点粒，可以继续向下衍生出新的粒群。下面以N1，1，1向下衍生为例。粒N1，1，1包含的对象为O1，1，1={1，2，3}，由于f（1）={a，b，g}，所以得到O1，1，1相对于{a，b，g}c的最简非完全覆盖{h}。从而N1，1，1的子粒为N1，1，1，1=（abgh，23，23）。二者构成的粒群为（N1，1，1;N1，1，1，1），如图5所示。

此时将水生动物分为N1，1，1，1所代表的有四肢的水生动物和O1，1，1-g（h）所表示的没有四肢的水生动物两类。

同理可得O1，1，1，1相对于{a，b，g，h}c的最简非完全覆盖{c}，从而N1，1，1，1向下衍生出子粒N1，1，1，1，1=（abghc，3，3）。由于f（3）={a，b，g，h，c}，所以根据推论1知N1，1，1，1，1是一个终点粒，至此不能再向下衍生出粒群了。同时，将N1，1，1，1，1所代表的有四肢的两栖动物“青蛙”和O1，1，1，1-g（c）所表示的有四肢的非两栖水生动物“娃娃鱼”区分开来。

对于其他粒也可类似讨论，最终的属性偏序形式结构图如图6所示。

以上展示了对于给定的形式背景，如果根据数学形式化描述来构造属性偏序形式结构。同时，通过对“青蛙”和“娃娃鱼”的区分和认识的过程，可以认识到，在属性偏序形式结构中，随着层次的加深，粒中的属性不断叠加，粒所描述的对象范围逐渐缩小，最终实现对具体对象的认识和区分的目的，这与人类认知客观事物的规律是一致的。

4结论

属性偏序形式结构是一种具有可视能力的知识发现和知识表示的理论。本文针对该理论的研究多集中在算法和应用方面，而基础理论的抽象数学化研究不足的问题，探讨了属性偏序形式结构的数学形式化描述。首先，基于粒计算的思想提出了知识表示的形式化框架，即数据、粒和粒间结构所组成的三元组。在此基础上，通过定义属性的覆盖基数、对象集合的覆盖和最简覆盖，给出了属性偏序形式结构的粒和粒群的概念，即粒群是由顶点粒所包含的对象集的最简覆盖所确定的雙层多元组，并且粒群中的子粒在一定条件下有衍生出新粒群的能力。最终，通过给出属性偏序形式结构中的粒衍生出粒群的充要条件，解决了属性偏序形式结构的构造，从而完成了该理论的数学形式化描述。最后，通过具体实例展示了利用数学形式化描述构造属性偏序形式结构的过程，以及其中体现的人类认知客观事物的规律。

参考文献

[1] 李金海， 闫梦宇， 徐伟华， 等. 概念认知学习的若干问题与思考 [J]. 西北大学学报（自然科学版）， 2020， 50（4）： 501-515.

LI J H，YAN M Y， XU W H， et al. Some problems and thoughts on concept-cognitive learning [J]. Journal of Northwest University （Natural Science Edition）， 2020， 50（4）： 501-515.

[2] 李金海， 米允龙， 刘文奇. 概念的渐进式认知理论与方法 [J]. 计算机学报， 2019， 42（10）： 2233-2250.

LI J H， MI Y L， LIU W Q. Incremental cognition of concepts： theories and methods [J]. Chinese Journal of Computers， 2019， 42（10）： 2233-2250.

[3] LI J H， MEI C L， XU W H， et al. Concept learning via granular computing： a cognitive viewpoint [J]. Information Sciences， 2015， 298：447-467.

[4] WILLE R. Restructuring lattice theory： an approach based on hierarchies of concepts [M]// RIVAL I. Ordered Sets. Dordrecht， Holland： D. Reidel Publishing Company， 1982： 445-470.

[5] LI K W， SHAO M W， WU W Z. A data reduction method in formal fuzzy contexts [J]. International Journal of Machine Learning and Cybernetics， 2017， 8（4）： 1145-1155.

[6] SHAO M W， LI K W. Attribute reduction in generalized one-sided formal contexts [J]. Information Sciences， 2017， 378： 317-327.

[7] LI J， WANG X， WU W， et al. Attribute reduction in inconsistent formal decision contexts [J]. International Journal of Machine Learning and Cybernetics， 2017， 8（1）： 81-94.

[8] WU W Z， QIAN Y H， LI T， et al. On rule acquisition in incomplete multi-scale decision tables [J]. Information Sciences， 2017， 378： 282-302.

[9] MI Y L， LIU W Q， SHI Y， et al. Semi-supervised concept learning by concept-cognitive learning and concept space [J]. IEEE Transactions on Knowledge and Data Engineering， 2022， 34（5）： 2429-2442.

[10] MI Y L， SHI Y， LI J H， et al. Fuzzy-based concept learning method： exploiting data with fuzzy conceptual clustering [J]. IEEE Transactions on Cybernetics， 2022， 52（1）：582-593.

[11] HONG W X， LI S X， YU J P， et al. A new approach of generation of structural partial-ordered attribute diagram [J]. ICIC Express Letter， Part B： Applications， 2012， 3（4）： 823-830.

[12] 洪文学， 李少雄， 张涛， 等. 大数据偏序结构生成原理 [J]. 燕山大学学报， 2014， 38（5）： 388-393.

HONG W X， LI S X， ZHANG T， et al. The generation principle of partial-ordered structure towards big data [J]. Journal of Yanshan University， 2014， 38（5）： 388-393.

[13] FAN F J， HONG W X， SONG J L， et al. A method of attribute partial-ordered structure diagram for the composition structures of prescription and knowledge discovery [J]. ICIC Express Letters， 2016， 10（3）： 593-600.

[14] YAN E L， SONG J L， HONG W X. Knowledge discovery and visualization of kidney-related pattern and treatment based on attribute partial-ordered structure diagram [J]. ICIC Express Letters， Part B： Applications， 2017， 8（9）： 1331-1338.

[15] YAN E L， SONG J L， LIU C N， et al. A research on syndrome element differentiation based on phenomenology and mathematical method [J]. Chinese Medicine， 2017， 12： 19.

[16] 李亞希， 刘超男， 洪文学. 基于属性偏序理论探讨李坤寅治疗子宫腺肌病用药规律[J]. 山东中医杂志， 2020， 39（6）： 560-564.

LI Y X， LIU C N， HONG W X. Discussion on Li Kunyin′s law of medication in treating adenomyosis based on attribute partial order theory [J]. Shandong Journal of Traditional Chinese Medicine， 2020， 39（6）： 560-564.

[17] 张晓希， 洪文学， 王晓颖，等. 基于属性偏序原理的老年2型糖尿病患者舌象特征研究[J]. 糖尿病新世界， 2021， 24（23）： 1-4.

ZHANG X X， HONG W X， WANG X Y， et al. Study on tongue features of elderly patients with type 2 diabetes based on attribute partial order principle [J]. New World of Diabetes， 2021， 24（23）： 1-4.

[18] YU J P， HONG W X， QIU C L， et al. A new approach of attribute partial order structure diagram for word sense disambiguation of English prepositions [J]. Knowledge-Based Systems， 2016， 95： 142-152.

[19] YU J P， LI C， HONG W X， et al. A new approach of rules extraction for word sense disambiguation by features of attributes [J]. Applied Soft Computing， 2015， 27： 411-419.

[20] 梁怀新， 宋佳霖， 郑存芳， 等. 肿瘤参数属性偏序结构可视化实现乳腺癌诊断[J]. 中国生物医学工程学报， 2018， 37（4）： 404-413.

LIANG H X， SONG J L， ZHENG C F， et al. Diagnosis of breast cancer based on tumor parameters and visualization of the attribute partial order structure diagram [J]. Chinese Journal of Biomedical Engineering， 2018， 37（4）： 404-413.

[21] LIU J， WANG X， ZHANG Y， et al. A method of image mining based on the attribute partial order structure diagram [J]. ICIC Express Letters， Part B： Applications. 2014， 5（5）： 1473-1479.

[22] 孫良刚. 基于属性偏序原理的属性偏序结构图表示算法研究 [D]. 秦皇岛： 燕山大学， 2012.

SUN L G. Research on representation algorithm of attribute partial order structure graph based on attribute partial order principle [D]. Qinhuangdao： Yanshan University， 2012.

[23] 李少雄， 闫恩亮， 宋佳霖， 等. 偏序结构图的一种计算机生成算法[J]. 燕山大学学报， 2014， 38（5）： 403-408.

LI S X， YAN E L， SONG J L， et al. Computational generation algorithm of partial ordered structure diagram [J]. Journal of Yanshan University， 2014， 38（5）： 403-408.

[24] 郑存芳， 李少雄， 栾景民， 等. 偏序结构环形图： 一种大数据偏序结构可视化新方法[J]. 燕山大学学报， 2014， 38（5）： 409-415.

ZHENG C F， LI S X， LUAN J M， et al. Structural partial-ordered circular diagram： structural partial-ordered visualization method of big data [J]. Journal of Yanshan University， 2014， 38（5）： 409-415.

[25] YAN E L， SONG J L， REN Y L， et al. Construction of three-way attribute partial order structure via cognitive science and granular computing [J]. Knowledge-Based Systems， 2020， 197： 105859.

[26] YAO Y Y. Three-way granular computing， rough sets， and formal concept analysis [J]. International Journal of Approximate Reasoning， 2020， 116： 106-125.

Mathematical formalization of attribute partial order formal structure

Abstract： Attribute partial order formal structure， as a new theory of knowledge discovery and knowledge representation based on human cognitive principles and granular computing ideas， has been widely used at present. However， its theoretical basis is lack of abstraction and mathematization， which is bound to affect the systematic development of this theory. Regarding the above problem， the mathematical formal description of attribute partial order formal structure is studied. Firstly， a formal framework of knowledge representation is proposed based on the idea of granular computing. On this basis， by defining the cover and the simplest cover of an object set， the concepts of granule and granular group of attribute partial order formal structure are given. And then through the discussion of the sufficient and necessary condition for a granule to derive a granular group， the knowledge structure in attribute partial order formal structure is given， so as to complete the mathematical formal description of attribute partial order formal structure. Finally， through specific examples， the process of constructing attribute partial order formal structure by using mathematical formal description is demonstrated， and the human cognitive law embodied in this process is revealed as well.

Keywords： formal context; mathematical formalization; attribute partial order formal structure; granular computing; concept cognitive learning